基于DSP的纸机滚动轴承故障诊断
郭文强, 夏令君, 齐 璐, 刘乐乐, 张宝嵘, 彭 程
(1.陕西科技大学 电气与信息工程学院, 陕西 西安 710021; 2.63751部队, 陕西 西安 710038)
基于DSP的纸机滚动轴承故障诊断
郭文强1, 夏令君1, 齐璐1, 刘乐乐2, 张宝嵘1, 彭程1
(1.陕西科技大学 电气与信息工程学院, 陕西 西安710021; 2.63751部队, 陕西 西安710038)
摘要:为解决传统滚动轴承检测方法实时性差、准确率低的问题,本文提出了一种DSP与Mallat算法以及BP神经网络相结合的纸机滚动轴承故障诊断方法.首先用振动传感器采集滚动轴承振动信号,然后将采集到的振动信号经过AD转换传输到DSP中,并经过Mallat算法处理将振动信号分解为BP神经网络所需的特征量,最后通过BP神经网络判断出故障的类型.实验结果表明,基于DSP的纸机滚动轴承故障诊断方法具有较好的实时性和准确性.
关键词:纸机; 轴承; 故障诊断; DSP; 神经网络
0引言
在生产生活中,造纸业一直占据着重要的地位.随着科技的进步,纸张产量越来越高,随之而来纸机的造价亦越来越昂贵、结构越来越复杂,一旦出现故障将会造成巨大损失.滚动轴承是纸机中使用最多的零部件,据统计,一台纸机中大概有500多个滚动轴承[1],而且滚动轴承工作环境恶劣,不同的轴承寿命相差很大,难以预测.传统的滚动轴承检测方法有油膜电阻法、温度分析法、油样分析法、噪声分析法、频谱分析法[2]等.以上方法均存在结果不准确、成本高等缺陷.而振动信号分析方法则存在准确率高、易于分析等优点,故得到了广泛的应用.
轴承正常运行时,振动信号能量主要集中在低频段,当轴承出现故障时,故障引起的冲击脉冲会激发轴承的高频振动.小波分解中的Mallat算法能够将信号分解为不同频率的信号,随着分解层数的增加,信号的分解都能够达到更精细的程度,能够有效地提取出振动信号不同频率带的特征信号.
BP神经网络是目前使用最广泛的算法模型之一,具有非线性映射能力、自学习自适应能力以及较强的容错能力.经过训练,能够得到一个有效的滚动轴承故障诊断模型.
为得到一个准确性高、实时性好的滚动轴承故障诊断模型,本文将Mallat算法和BP神经网络两种算法相结合,并固化到DSP中,充分利用DSP信号处理的优势对纸机滚动轴承状态进行了实时诊断.
1滚动轴承振动原理及故障分类
当轴承在一定速度下运转时,轴承的工作条件和加工误差以及本身的故障因素会对轴承振动系统产生激励,从而使轴承产生振动.
滚动轴承具有相当复杂的振动和噪声,有些是由轴承本身结构特点引起的;有些是和制造装配有关,如滚动体和滚道的表面波纹、表面粗糙度以及几何精度不够高等,在运转中都会引起振动和噪声.
正常情况下,滚动轴承振动频率较低,当滚动轴承出现故障的时候,故障部位就会产生周期性的高频振动.其故障振动信号脉冲宽度在us数量级,将激起系统或结构的高频响应,响应水平取决于故障的类型.不同的故障会产生不同的振动频率和振幅,因此,根据不同的振动信号可以分辨出不同的故障类型.
按照故障原因,常见的滚动轴承故障有磨损失效、疲劳失效、腐蚀失效、破损失效、压痕失效、胶合失效、烧伤失效[3];按照故障发生的位置,可以分为正常、内圈故障、外圈故障和滚动体故障.
2系统组成
为了能够快速地运行Mallat算法和BP神经网络算法,需要处理芯片具有超高的主频和强大的信号处理能力.DSPTMS320C6748为功耗最低浮点型DSP芯片,采用TI第三代超长指令集,主频最高700 MHz,整个系统由四个部分组成:(1)信号采集模块负责纸机滚动轴承的振动信号采集,包括AD采样、信号放大等功能;(2)逻辑控制模块负责控制整个系统,包括控制AD采集、数据的缓存以及工作方式的切换;(3)信号处理模块是整个系统的核心,负责算法的运行和振动信号处理以及LCD结果显示;(4)电源模块负责整个系统的供电.系统组成如图1所示.
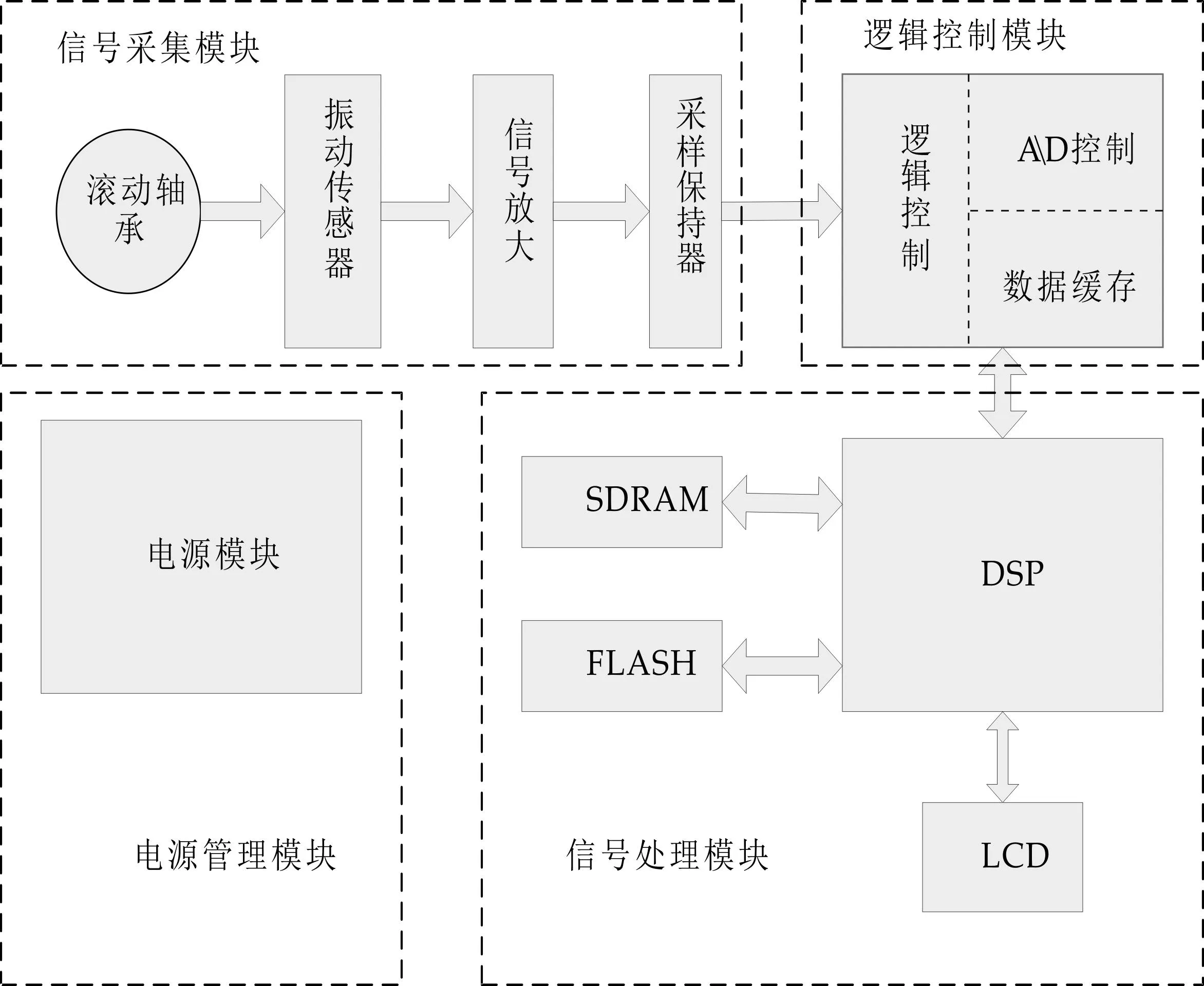
图1 系统结构图
软件开发采用Matlab和CCS混合编程的方式完成程序的开发.常用的DSP开发语言有C语言和汇编语言.C语言结构清晰,简单明了,更容易开发;汇编语言执行速度快但编写难度大.本文采用汇编语言与C语言相结合的方式设计开发.其中,汇编语言用于开发较为简单的Mallat算法程序,并作为子函数来调用,对于复杂度较高的BP神经网络程序则采用C语言开发.
3振动信号的Mallat算法分解
3.1 Mallat算法原理
Mallat算法能够将信号多级分解,从而获得更精确的信号分量,如图2所示.在图2中,a0为原始信号、d(n)为第n层的高频分量、a(n)为低频分量.
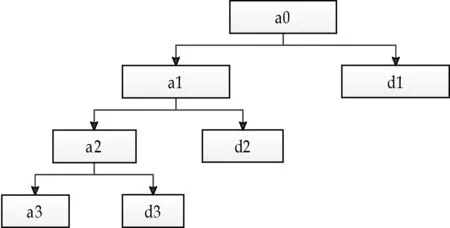
图2 Mallat算法的三级分解图
在信号分解的过程中,原信号a(n-1)通过分别与高通滤波器和低通滤波器卷积,然后经过下抽样每隔一个元素抽取一个元素组成一个新的序列,即可得到低频信号a(n)和高频信号d(n),如图3所示,其信号分解过程可用公式(1)~(2)实现[4].
dj+1(n)=aj(n)*H_d(n)=

aj+1(n)=aj(n)*G_d(n)=

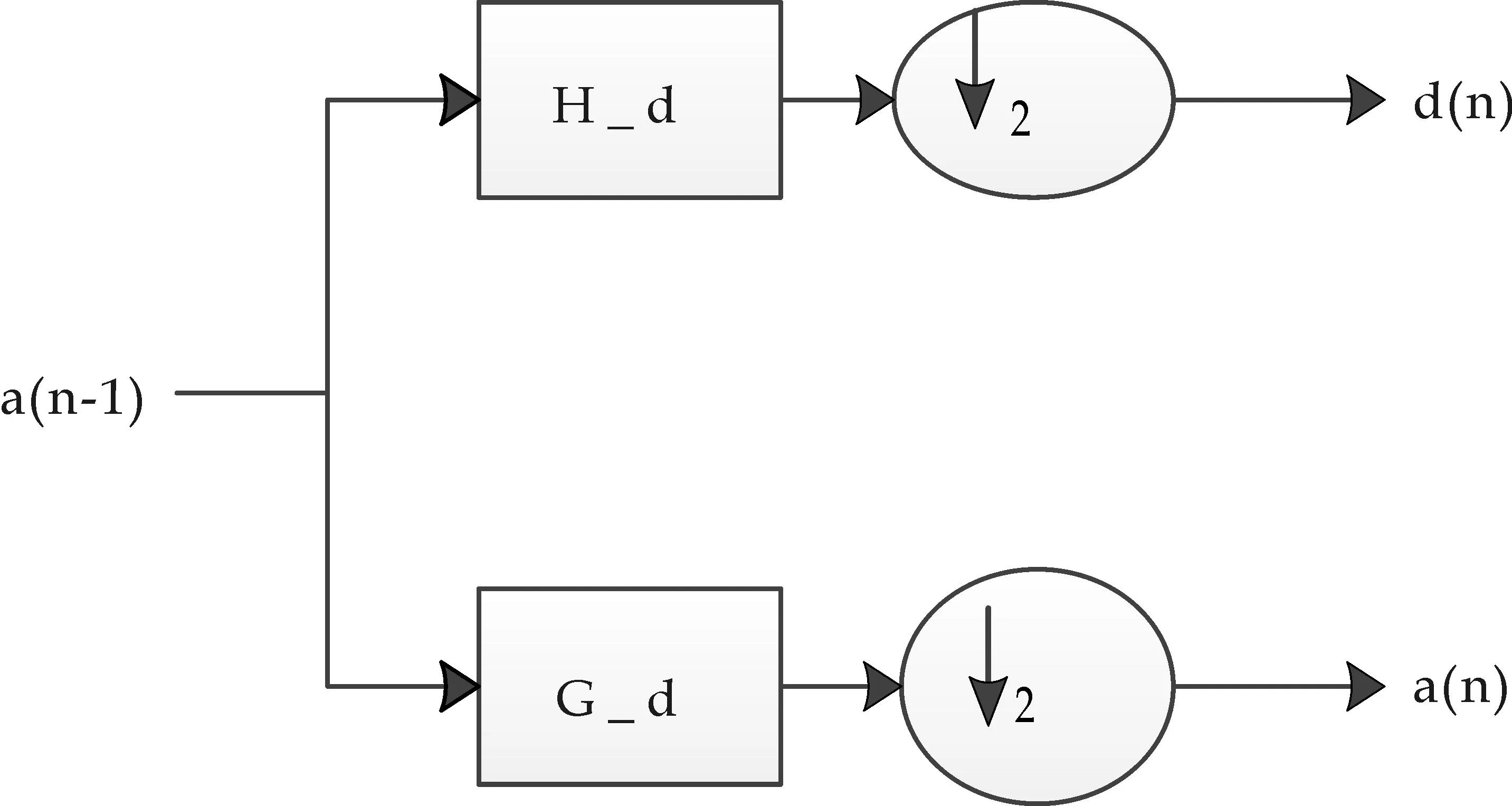
图3 Mallat算法的分解原理图
利用Matlab的wfilters(‘wave name’)可以获取4个滤波器系数,具体命令如下:
[Lo_D,Hi_D,Lo_R,Hi_R]=wfilters(′db1′)
3.2 Mallat算法的DSP实现
Mallat算法又被称为快速小波变换,这从空间概念上形象地说明了小波的多分辨率特性.随着变换尺度的变化,可以观察到信号不同频率下的特征.
Mallat算法的DSP实现过程使用了大量的积分运算,普通的寻址方式会增加处理的运算强度,从而降低运算速度.这里采用DSP独特的循环寻址方式,循环寻址是寄存器寻址的方式之一,其原理如图4所示.
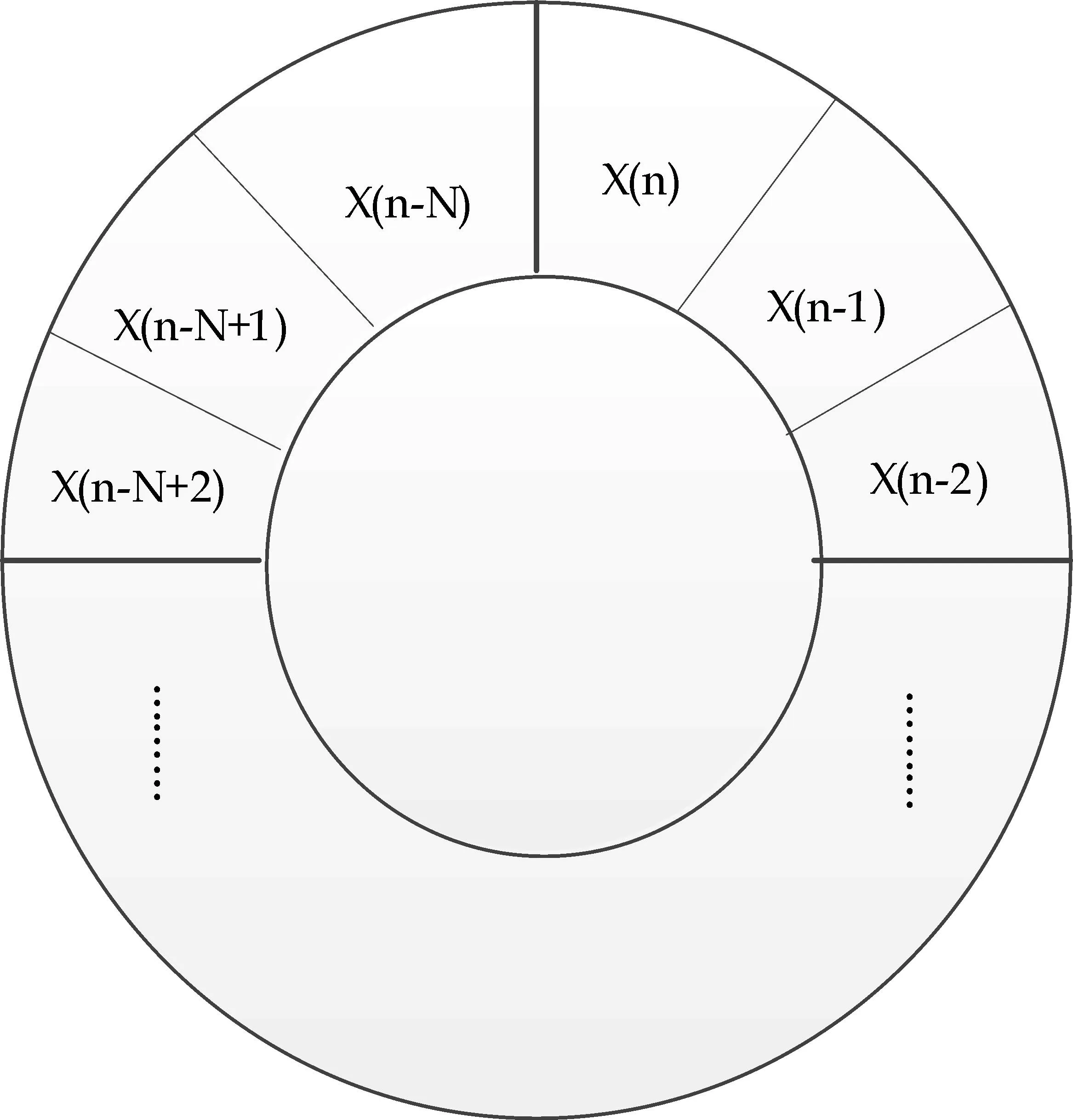
图4 循环寻址原理图
循环寻址涉及到一个循环缓冲区,其缓冲区的数据x(n)由指针定位,数据的第一次写入从x(n)开始,按顺时针方向连续写入,新数据会被写到x(n),数据会以此类推到x(n-N),数据的总长度为N.在计算的时候,指针从x(n)开始指向下一个数据的位置,直到x(n-N).当有新的数据要写入时,指针会沿逆时针方向指向x(n-N),周而复始直到整个计算完成[5].
Mallat算法主要是在两个循环中完成的.其中,内循环通过系数与输入数值的相乘累加得到一个尺度值;外循环则是保证每次内循环执行完成后指针正确的平移.DSP中对应核心代码如下:
RPTS @L UPPER//循环次数
MPYF*AR0++%,*AR2,R0//输入序列与小波系数运算
||ADDF R0,R2//并行执行ADDFR0,R2
特征量太少会影响BP神经网络的训练准确度,太多则会加大运算量,造成运算速度过慢.实验中发现,为了达到较好的训练效果,本文采用四个特征量来训练BP神经网络,Mallat算法每次只对低频进行分解,需要进行三级分解方可得到四个特征量.
图5(a)为滚动轴承内圈故障3点方向振动信号波形图,采样率为12 k/s;图5(b)为振动信号经过Mallat一次分解后的高低频两个分量,两个分量的信号波形差异很大,低频分量反应了原始波形的大致走向,高频分量则包含了故障信号;图5(c)为一次分解后的低频分量;经过二次分解后的高低频分量;图5(d)为二次分解后的低频分量三次分解后的高频分量和低频分量.从图5可以看出,随着分解次数的增加,分解的高频分量越来越小,不同频率的振动信号分量振幅和频率都不相同.
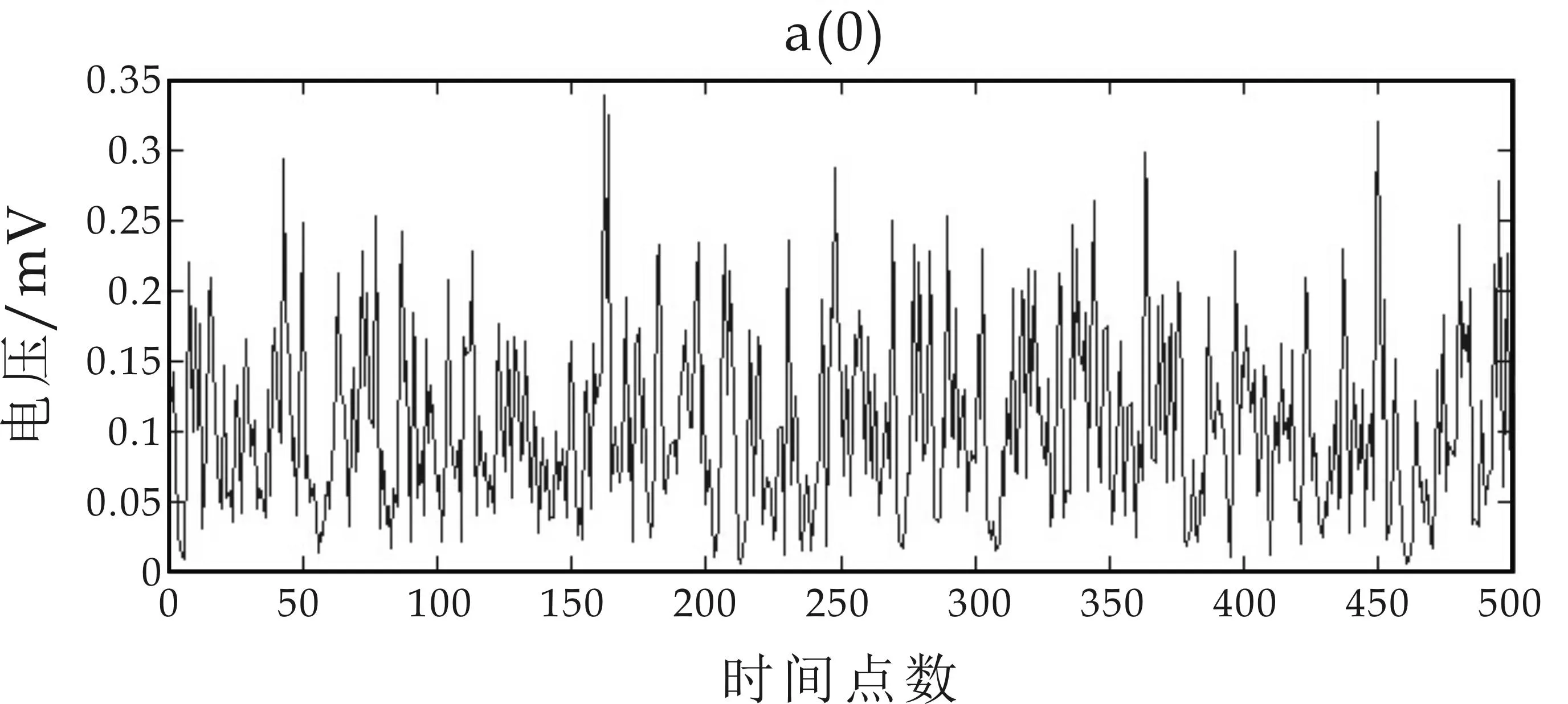
(a)内圈故障振动信号波形图

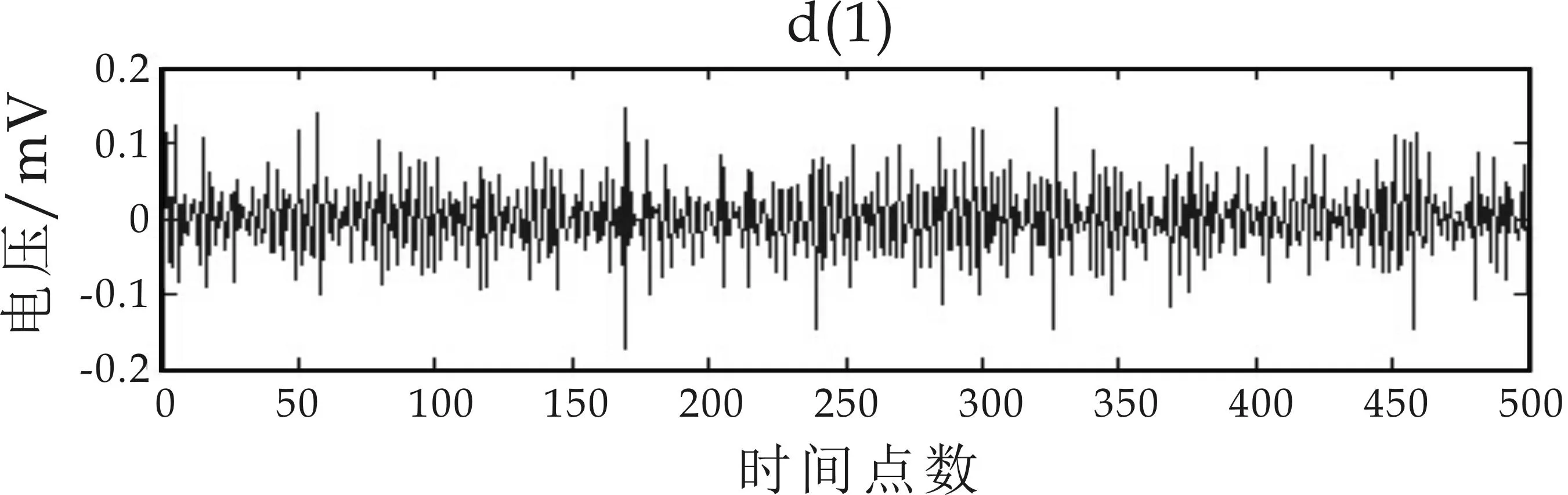
(b)一次分解后的高低分量波形图
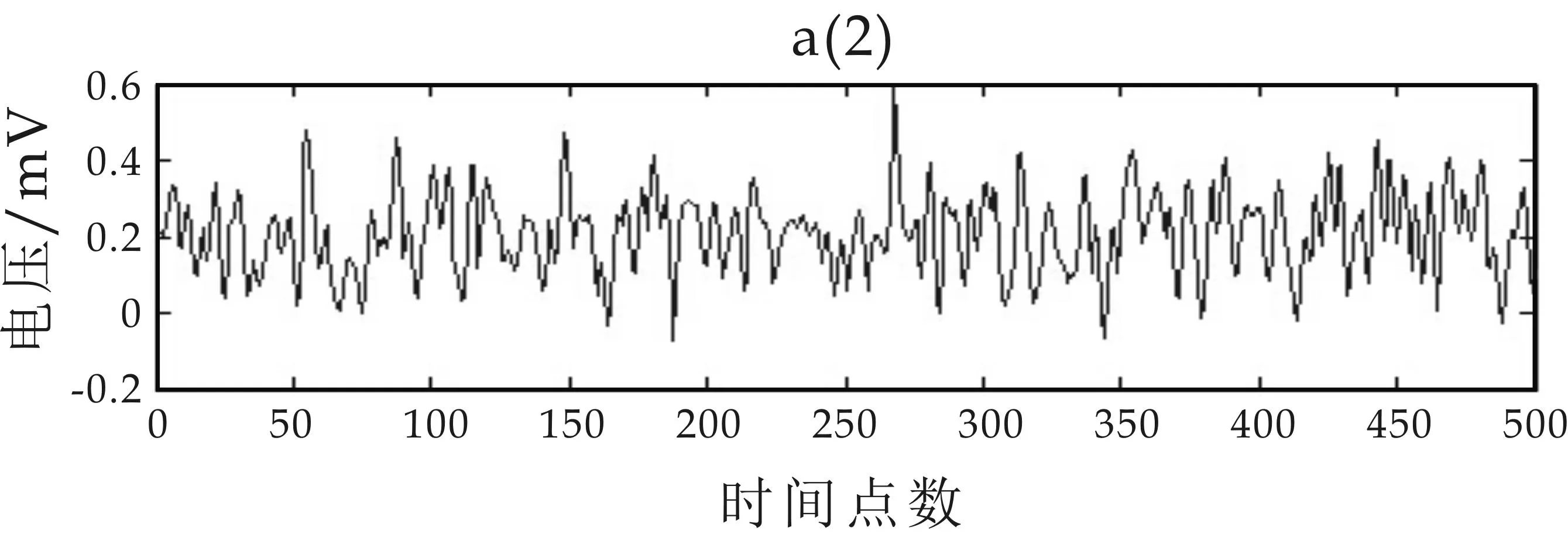
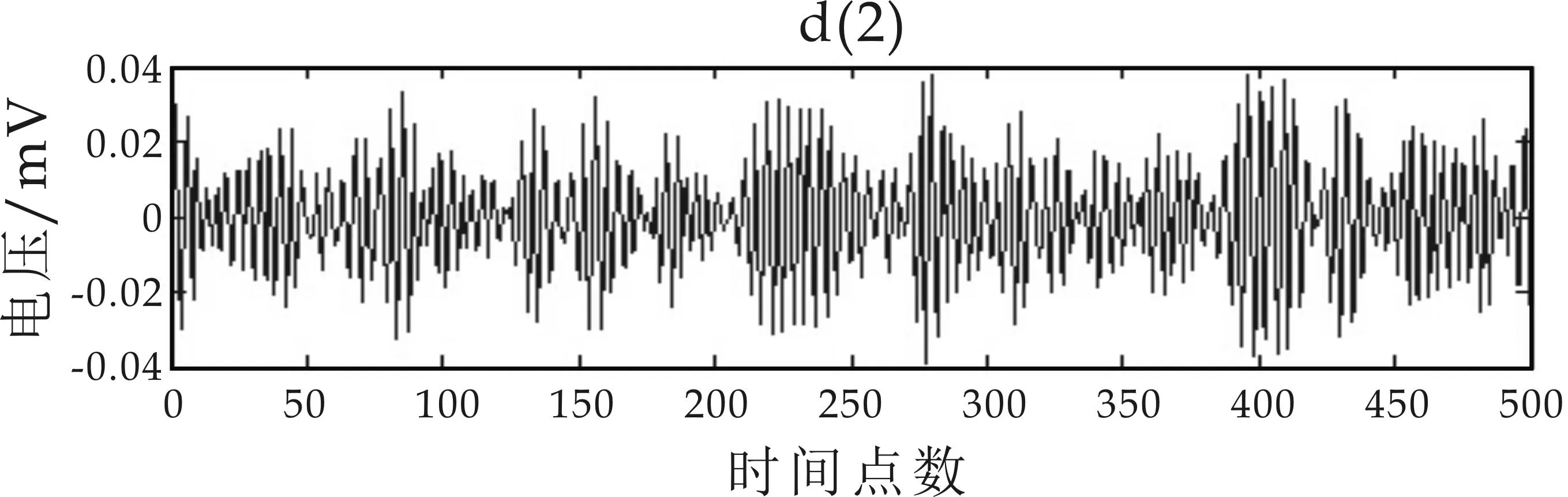
(c)二次分解后的高低频信号波形
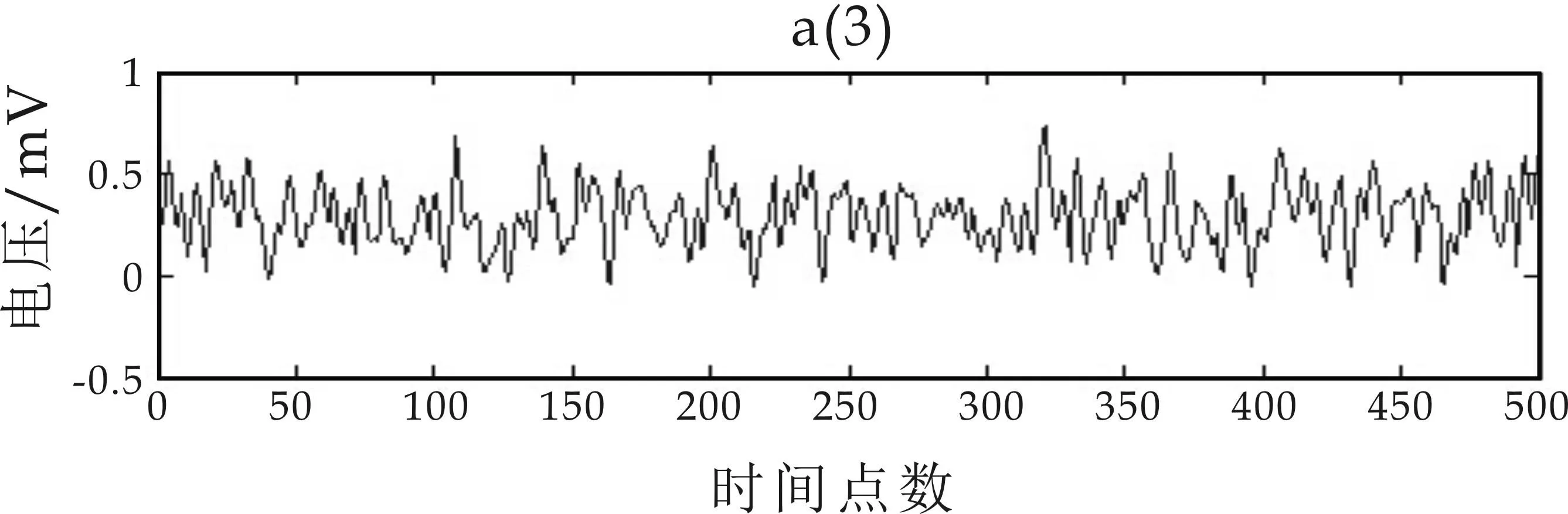
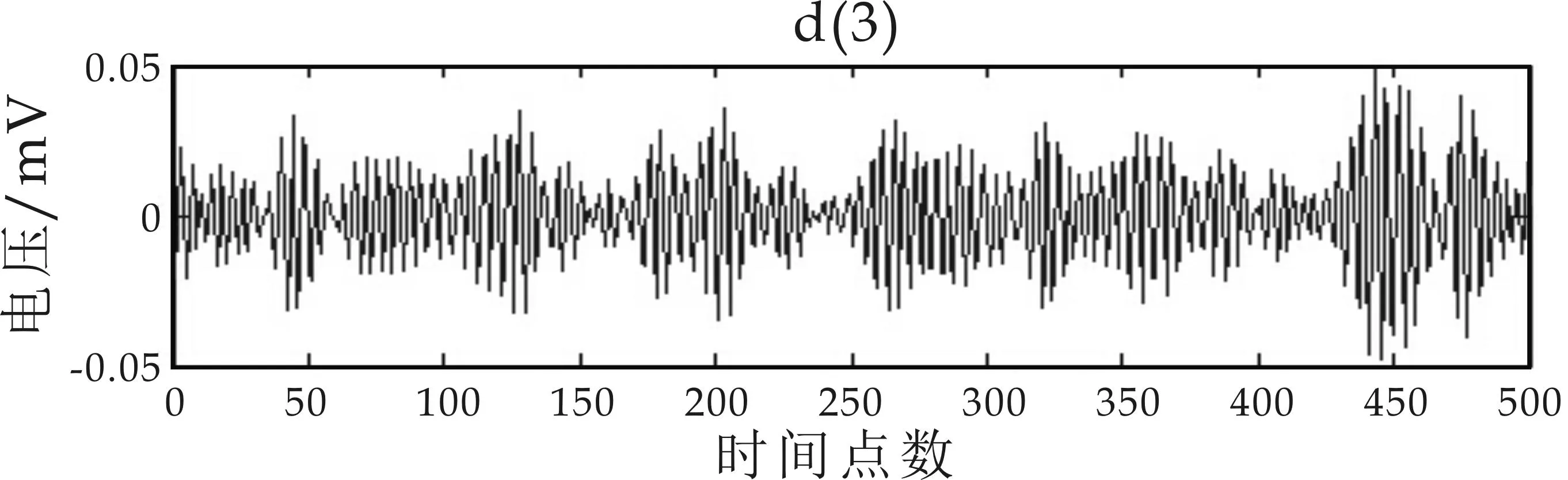
(d)三级分解后的高低频分量图5 Mallat分解前后振动信号波形图
4BP神经网络的DSP实现
BP神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一.
BP神经网络的DSP实现包括两个部分:神经网络模型的训练和滚动轴承故障推理.
4.1 模型训练
Kolmogorov定理[6]表明任何连续函数f(x)能被三层前馈神经网络实现,其中,隐层结点数s=2n+1(n为输入层结点数).图6为滚动轴承振动信号处理的BP神经网络模型,该模型包括输入层、输出层、隐含层.其中,输入层包含四个节点,分别为I(1)、I(2)、I(3)、I(4);隐含层为1层,共包含9个节点,分别为Y(1)、Y(2)、Y(3)、Y(4)、Y(5)、Y(6)、Y(7)、Y(8)、Y(9);输出层包含两个节点,分别为O(1)和O(2).BP神经网络的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,从而使网络的误差平方和最小.
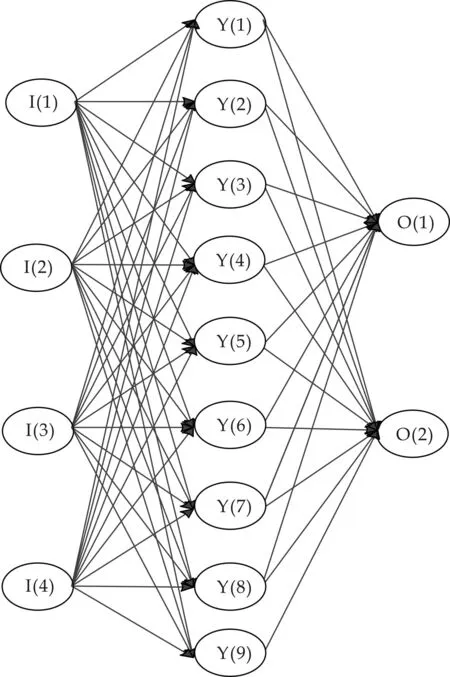
图6 BP神经网络模型
本文采用Altera公司的DSP开发平台CCS集成开发环境开发DSP程序,编程语言为C语言,程序开发完成编译无误后通过仿真器下载到DSP的Flash rom中.
DSP中BP神经网络的具体构建过程如下:
(1)第一步:定义训练实例x(n)和y(n),网络模型为NET.
网络结构定义DSP对应程序代码如下:
typedef struct //网络定义
{
LAYER **Layer; //隐含层
LAYER *Inputlayer; //输入层
LAYER *Outputlayer; //输出层
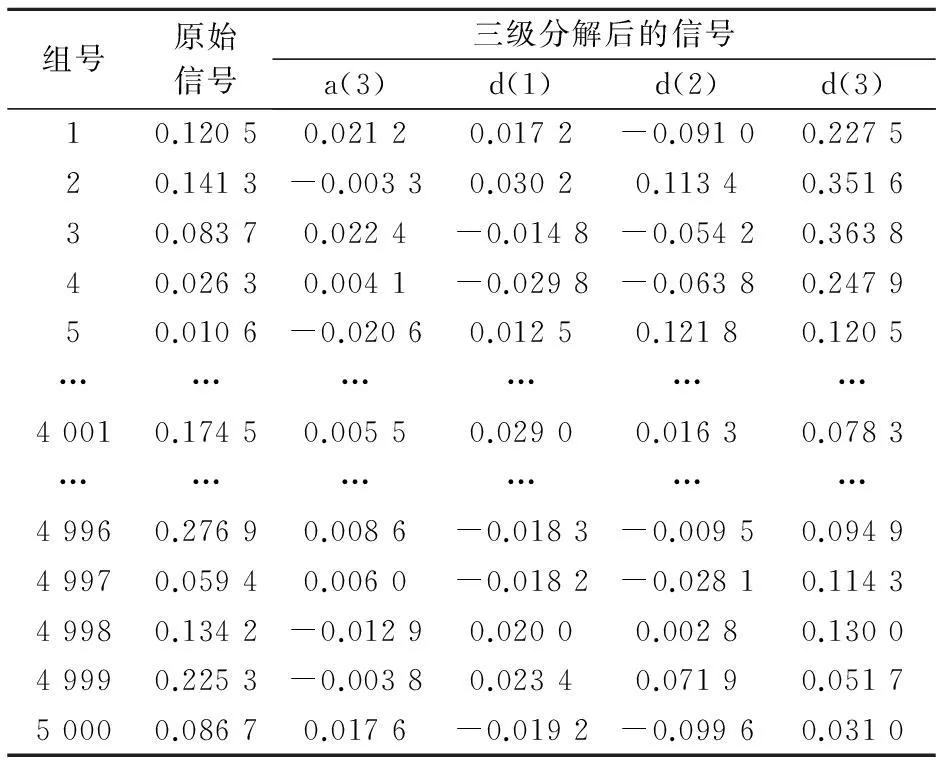
float Error; //允许误差
float Eta; //学习率
}NET;
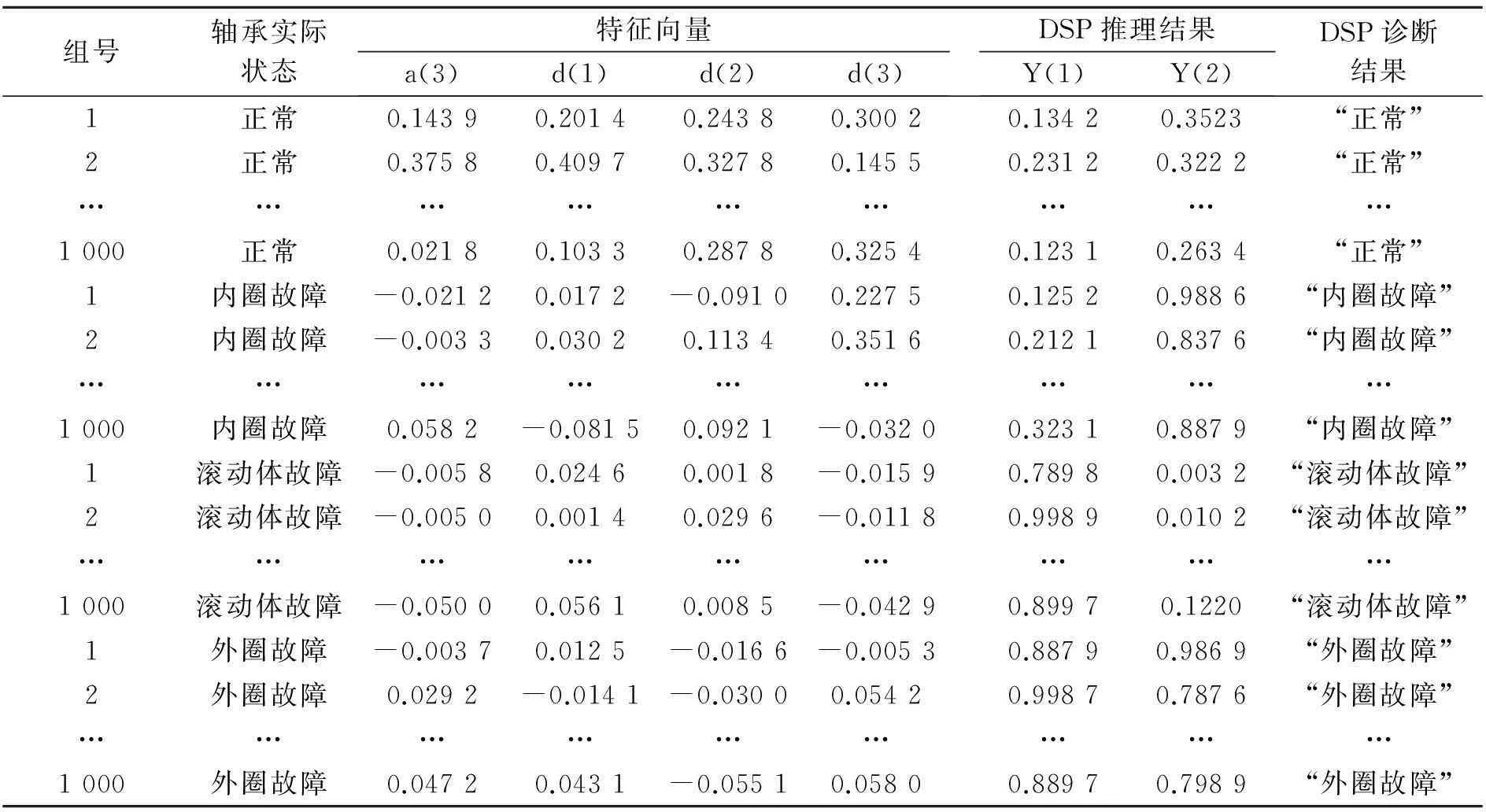
该段代码定义了BP神经网络结构,其中包括隐含层Layer、输入层Inputlayer、输出层Outputlayer、允许误差Error、学习率Eta.
(2)第二步:初始化权值,权值初始化通过Randomreal语句产生0~1之间的随机数来完成,代码如下:
void RandomWeights(NET *Net)
{
int l,i,j;
for(l=1;l for(i=1;i <= Net->Layer[l]->Units;i++) for(j=0;j <= Net->Layer[l-1]-> Units;j++) Net->Layer[l]->Weight[i][j]= RandomReal(); return; } (3)第三步:网络正向传播,依次求出各层节点输出值. (3) 正向传播主要代码如下: Void PropagateLayer (NET*Net,LAYER *Lower,LAYER *Upper//层间顺传播 { int i,j; float sum; for(i=1;i <=Upper->Units;i++) { sum= 0; for(j=1;j<=Lower->Units;j++) sum+= (Upper->Weight[i][j] * Lower->Output[j]); Upper->Output[i]=(float)(1/(1+ exp(-sum)));//输出结果传递 } return; } 正向传播的过程是在两个循环内完成的.其中,外循环i在层间循环,内循环j在节点之间循环.利用公式(3)计算出每个节点的输出Output[i]. (4)第四步:网络反向传播,计算传播误差,修正权值. (4) 反向传播过程的主要代码如下: void BackpropagateLayer(NET *Net,LAYER *Upper,LAYER *Lower) { int i,j; float Out,Err; for(i=1;i<=Lower->Units;i++) { Out=Lower->Output[i]; Err= 0; for(j=1;j<=Upper->Units;j++) Err+=(Upper->Weight[j][i]* Upper->Error[j]); Lower->Error[i] = Out*(1-Out)*Err; } return; } 反向传播的过程和正向传播的过程类似,也是在两个循环中完成.其中,外循环i用于层间循环,j用于节点间循环,不同的地方是传播方向以及输出值,反向传播通过公式(4)实现,输出值为各层误差值Error[i]. 权值调整部分代码如下: void AdjustWeights(NET *Net) { int l,i,j; float Out,Err; for(l=1;l for(i=1;i<=Net->Layer[l]->Units;i++) for(j=0;j<=Net->Layer[l-1]-> Units; j++) { Out=Net->Layer[l-1]->Output[j]; Err=Net->Layer[l]->Error[i];//节点误差 Net->Layer[l]->Weight[i][j]+= (Net->Eta*Err*Out); } return; } 权值调整过程包括三个循环,最外层的循环l在层间循环,中间层循环i在Upper层节点间循环,内层循环j在Lower层节点间循环,通过层间误差Error与节点输出Output、权值weight[i][j]相乘,并与原来权值相加得到新的权值. (5)第五步:进入下一次传播,检测误差 |target(i)-outlayer(i)->out| 若误差值大于预设值则转到第四步. (6)第六步:滚动轴承故障诊断模型存储. BP神经网络训练完成后,即可用于滚动轴承的故障推理,其推理过程和模型正向传播过程相同.模式切换时通过按键来控制,当BP神经网络训练误差小于最小误差时,程序会停止训练,并驱动相应的LED闪烁,通过相应的按键选择进入推理模式.推理数据来源于Mallat算法三级分解后四个频带的特征量,用于训练和诊断推理的数据不能重复. 当有振动信号输入DSP时,利用Mallat算法将振动信号分解为四个特征量,然后将特征量送进训练好的BP神经网络模型,经过推理输出层的两个节点输出,经过预设诊断阈值θ对比分析滚动轴承的故障类型.以下为内圈故障诊断DSP主要代码: for(i=1;i<=Net->Outputlayer->Units;i++) { if(fabs(Net->Outputlayer->Output[i]-0)<=Theta) &&(fabs(Net->Outputlayer->Output[i+1]-1)<=(1-Theta)) printf(“内圈故障”); } 诊断过程主要是对输出层两个节点值进行判断,该段代码是对滚动轴承内圈故障诊断结果进行判断,Theta(θ)是诊断阈值,内圈故障设为(01). 5实验结果分析 实验部分采用的是Case Western Reserve大学实验室采集的滚动轴承振动信号[7].在采集振动信号时分别在滚动轴承3点、6点和12点方向放置了3个振动传感器,采集的数据包括滚动轴承正常、内圈故障、外圈故障和滚动体故障四种状态;采 样率分别为12 k/s、24 k/s、48 k/s;实验中滚动轴承破损点直径分别为0.007 mils、0.014 mils、0.021 mils、0.028 mils,本文选用0.007 mils 对应数据. 应用本文提出的DSP诊断方法进行轴承状态诊断实验.实验中取BP神经网络训练误差Err=0.01,诊断阈值θ取为0.618.具体实验结果见表1~2所示. 表1 轴承内圈故障振动原始信号和 表2 基于DSP的滚动轴承诊断结果(推理诊断阈值θ=0.618) 表1为滚动轴承内圈故障原始振动信号数据和Mallat算法三级分解后的四个特征量数据,共5 000组,其中采样率为12 k/s.实验中样本训练数据为4 000组,测试数据为1 000组. 表2中的数据为DSP利用训练完成的BP神经网络模型故障诊断情况.其中,四个特征量分别为Mallat算法三级分解后的四个频带的振动信号分量: a(3) 、d(3)、 d(2) 、d(1),诊断结果包括滚动轴承的四种状态:正常状态、内圈故障、滚动体故障和外圈故障. 实验结果为: (1)1 000组样本数据,滚动轴承正常情况下诊断准确率为100%,内圈故障情况下诊断准确率为98.82%,滚动体故障诊断准确率为98.64%,外圈故障诊断准确率为97.25%;平均故障诊断正确率为98.68%,高于文献[8]的95.28%. (2)BP神经网络平均训练时间为3~5秒(4 000组样本数据);诊断推理时间为1.786微秒,低于文献[8]时域诊断法所需的6.280~7.200毫秒诊断耗时. (3)根据Case Western Reserve大学公布的数据显示,最大采样率为48 k/s,实验用数据涉及滚动轴承破损直径为0.007 mils.由于轴承破损直径是0.007~0.028 mils中最小值,类似于滚动轴承早期故障,可见该方案能同时满足滚动轴承故障诊断的实时性和准确性要求. 6结论 本文提出了一种基于DSP的纸机滚动轴承故障诊断方法,实现了Mallat算法和BP神经网络在DSP中的运行.经过大量实验验证,该方案对于纸机滚动轴承的故障类型判断准确率高,甚至能够检测出滚动轴承早期故障,并且克服了以往纸机滚动轴承故障诊断设备实时性差的缺点. 参考文献 [1] 肖方煜.改进的小波阈值去噪算法及其在纸机滚动轴承故障振动信号预处理中的应用[D].西安:陕西科技大学,2013. [2] 杨云云.造纸机干燥部滚动轴承的故障诊断研究[D].西安:陕西科技大学,2012. [3] 万猛.基于贝叶斯网的轴承失效分析应用研究[D].郑州:河南科技大学,2013. [4] 吴多,程多福.基于DSP的快速小波分解和重构[J].吉林大学学报,2004,22(3):214-218. [5] 李仁刚,李少青,范小飞.DSP处理器循环寻址方式的设计与实现[C]//第十一届计算机工程与工艺学术会议.安徽黄山:中国计算机学会计算机工程与工艺专业委员会,2007:199-201. [6] 黄丽.BP神经网络算法改进及其应用研究[D].重庆:重庆师范大学,2008. [7] Bearing Data Center.Seeded fault test data[DB/OL].http://csegroups.case.edu/bearingdatacenter/,2015-05-24. [8] 沈长青.旋转机械设备关键部件故障诊断与预测方法研究[D].合肥:中国科学技术大学,2014. 【责任编辑:晏如松】 DSP based fault diagnosis of rolling bearing for paper-making machine GUO Wen-qiang1, XIA Ling-jun1, QI Lu1, LIU Le-le2, ZHANG Bao-rong1, PENG Cheng1 (1.College of Electrical and Information Engineering, Shaanxi University of Science & Techndogy, Xi′an 710021, China; 2.63751 Troops, Xi′an 710038, China) Abstract:In order to solve the problems of real-time and low accuracy for rolling bearing fault diagnosis,this paper presents a combination of Mallat algorithm and BP neural network based on DSP for paper-making machine fault diagnosis methods.Vibration signals from rolling bearing are acquired via vibration sensor controlled by DSP.After AD conversion,the vibration signals are decomposed as the feature vectors by Mallat algorithm and the diagnosis model is obtained based on the BP neural network coded in DSP which can determine the fault type.The experimental results show that the fault diagnosis method based on DSP for paper machine rolling bearing has good real-time performance and accuracy. Key words:paper-making machine; bearing; fault diagnosis; DSP; neural network 中图分类号:TH133.3;TP216 文献标志码:A 文章编号:1000-5811(2016)01-0148-06 作者简介:郭文强(1971-),男,陕西咸阳人,副教授,博士,研究方向:智能决策、故障诊断、无线传感器网络 基金项目:陕西省教育厅专项科研计划项目 (2013JK1114); 陕西科技大学博士科研启动 (BJ12-03) 收稿日期:*2015-10-13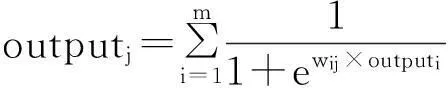
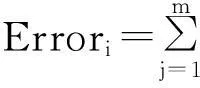
4.2 滚动轴承故障推理