具有周期传染率的SVEIR传染病模型的定性分析

杜燕飞， 曹　慧

(陕西科技大学 理学院， 陕西 西安　710021)



具有周期传染率的SVEIR传染病模型的定性分析

杜燕飞， 曹慧

(陕西科技大学 理学院， 陕西 西安710021)

摘要：研究了一类具有周期传染率的SVEIR传染病模型的动力学性态.定义了模型的基本再生数，得到了无病周期解全局稳定性的条件，讨论了系统的一致持续生存，并通过数值模拟展示了所得到的理论结果和模型复杂的动力学性态.

关键词：周期传染病模型； 基本再生数； 稳定性

0引言

众所周知，气候、环境和社会活动的周期性变化会导致一些传染病的爆发呈现周期性.例如麻疹、水痘、腮腺炎和风疹等，这几类传染病的发病数据都展示出明显的季节性波动现象[1,2]. 因此，当我们研究一些具有季节性的疾病时，应考虑人为活动和环境气候因素所引起的传染率的周期性变化，以描述季节性波动对模型的动力学性态的影响，使模型更具有一般性且符合实际.

目前，许多学者对具有周期性波动传染病的动力学行为进行了大量的研究[3-13]. 研究的成果主要集中在疾病的一致持续和消除、定义、计算基本再生数和相应的阀值理论、周期解的存在性和稳定性等.本文将建立一类具有周期传染率的SVEIR 模型，并研究其动力学性态.

1周期传染率的SVEIR模型

考虑感染者恢复后具有终身免疫力的传染病问题.我们把总人口分为易感者、接种者、潜伏者、染病者和恢复者5类，并且分别用S(t),V(t),E(t),I(t)和R(t)表示t时刻这5类个体的数量.Λ是人口增长率，p是新生儿的接种率，μ表示个体的自然死亡率. 假设部分接种者会产生并始终保持免疫力；而部分接种者会丧失免疫力，成为易感者.ε和α分别表示潜伏者的发病率和染病者的治愈率；γ表示接种人群丧失免疫力的比率. 假设疾病的传染率呈周期性，用β(t)表示染病者与易感者接触后成功感染的概率.本文考虑如下具有双线性传染率的非自治SVEIR传染病模型：

(1)

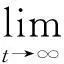
引理1系统(1)具有初始条件S(0)>0，V(0)>0,E(0)>0,I(0)>0,R(0)>0的解在[0,∞)上存在且为正.

由于系统(1)中的前四个方程中不含R(t)，且第五个方程是线性的，因此，我们仅需考虑由前四个方程所组成的模型，即系统(2)的动力学性态．

(2)

为了得到系统(2)的无病周期解，考察方程

(3)

2基本再生数

下面利用积分算子谱半径的方法来定义系统(2)的基本再生数. 系统(2)在无病周期解(S*(t),V*(t),0,0)的线性化系统所对应的感染者的方程为

(4)

3疾病的一致持续和消除

下面研究系统(2)的全局动力学性态.

定理1如果R0<1，则无病周期解(S*(t),V*(t),0,0)是全局渐近稳定的；反之，若R0>1，则它是不稳定的.

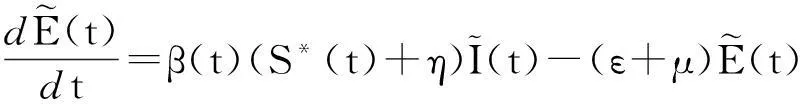
(5)

此系统等价于

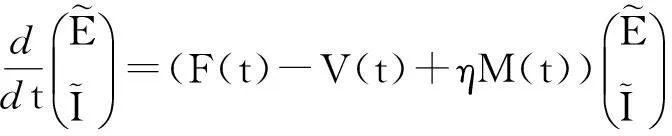
(6)

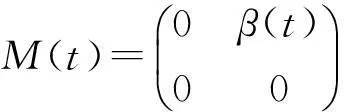
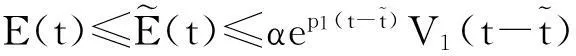
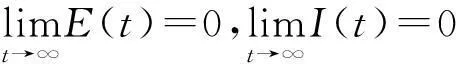
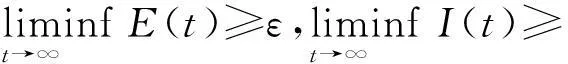
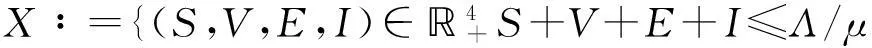
X0∶={(S,V,E,I)∈X∶E>0,I>0},

∂X0∶=X/X0.显然X0是正不变的，且∂X0是X的相对闭集. 记

M∂={(S0,V0,E0,I0)∈∂X0∶

pm(S0,V0,E0,I0)∈∂X0,∀m≥0}.

容易证明

M∂={(S,V,0,0)∶S≥0,V≥0}.

(7)

显然P在M∂上有唯一的不动点M0(S*,V*,0,0).

下证P关于(X0,∂X0)是一致持续的.由于R0>1当且仅当ρ(ΦF-V(ω))>1，可以选择取充分小的ξ>0，使ρ(ΦF-V+ξ M(ω))>1.注意到(3)的扰动系统

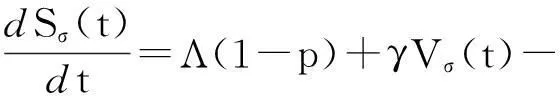
β(t)Sσ(t)σ-μSσ(t),

(8)

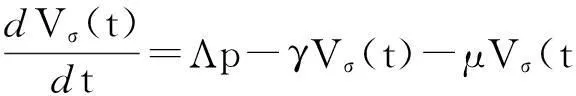
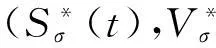
由解对初值的连续依赖性，存在δ0>0，使得当‖(S0,V0,E0,I0)-M0‖≤δ0时，有‖φ(t,(S0,V0,E0,I0))-φ(t,M0)‖<σ,t∈[0,ω].

现在可以断言

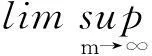
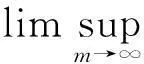
‖φ(t,Pm(S0,V0,E0,I0))-φ(t,M0)‖<σ.

进一步计算可得

‖φ(t,(S0,V0,E0,I0))-φ(t,M0)‖

=‖φ(t′,Pm(S0,V0,E0,I0))-φ(t′,M0)‖<σ

(9)

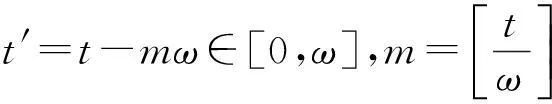
φ(t,(S0,V0,E0,I0))=(S(t),V(t),E(t),I(t)),由不等式(9)可推出0≤E(t)≤σ,0≤I(t)≤σ,t≥0.于是

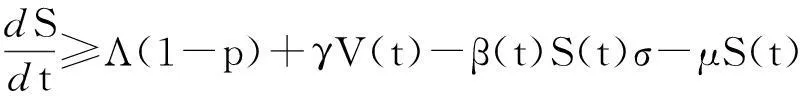
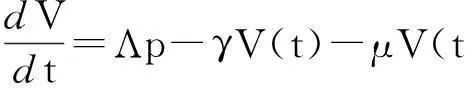
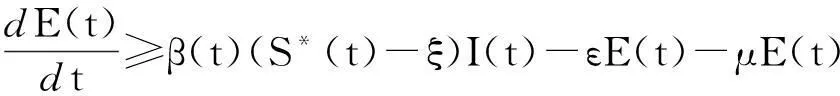
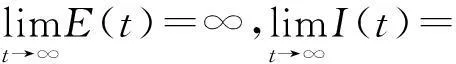
因为在M∂的每一条轨道收敛到M0，且M0在M∂中是非循环的. 由一致持续的非循环定理，P关于(X0,∂X0)是一致持续的.又由于M0在X中是孤立的，因此，由文献[14]中的定理3.1.1可知，系统(2)关于(X0,∂X0)是一致持续的.

进一步，由文献[14]中的定理1.3.6可得，(S*(t),V*(t),E*(t),I*(t)) 是系统(2)的一个严格正的ω周期解.

4数值模拟

下面利用数值模拟来验证所得的结论．对于模型(2),令参数Λ=0.02，p=0.85，γ=0.34,ε=0.5,α=0.2,μ=0.02，β0=0.14，β(t)=β0[1+0.6cos(2πt)],则基本再生数R0=0.97<1. 在图1中,模拟了具有初始条件s0=0.2,v0=0.2,e0=0.2,i0=0.2的解的渐近性态, 表明无病周期解是全局渐近稳定的，传染病最终消除.

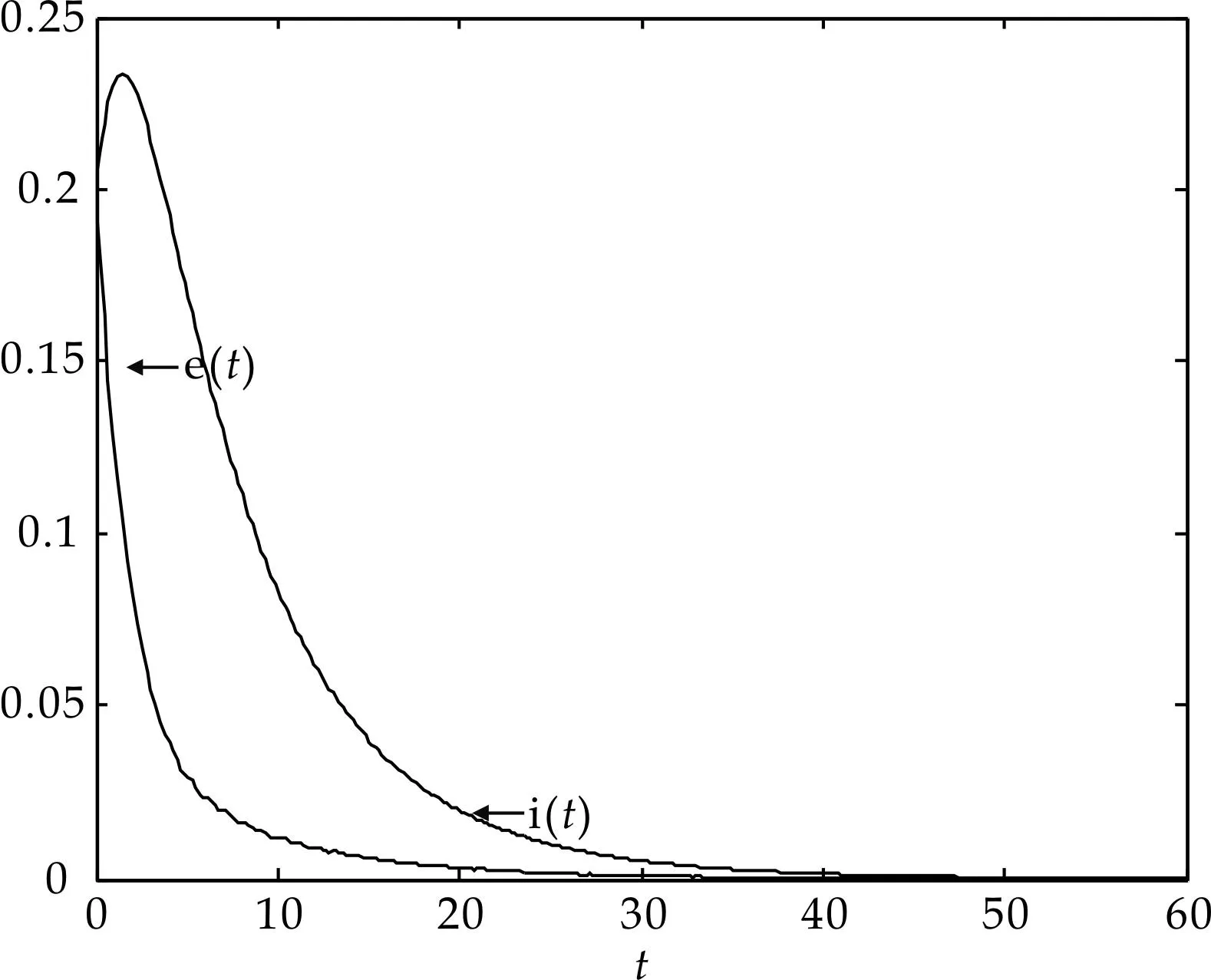
图1　疾病的消除

令Λ=0.14,p=0.5,β0=0.21,其它参数同图1,则基本再生数R0=6.24>1.图2的模拟结果说明了系统的一致持续生存.

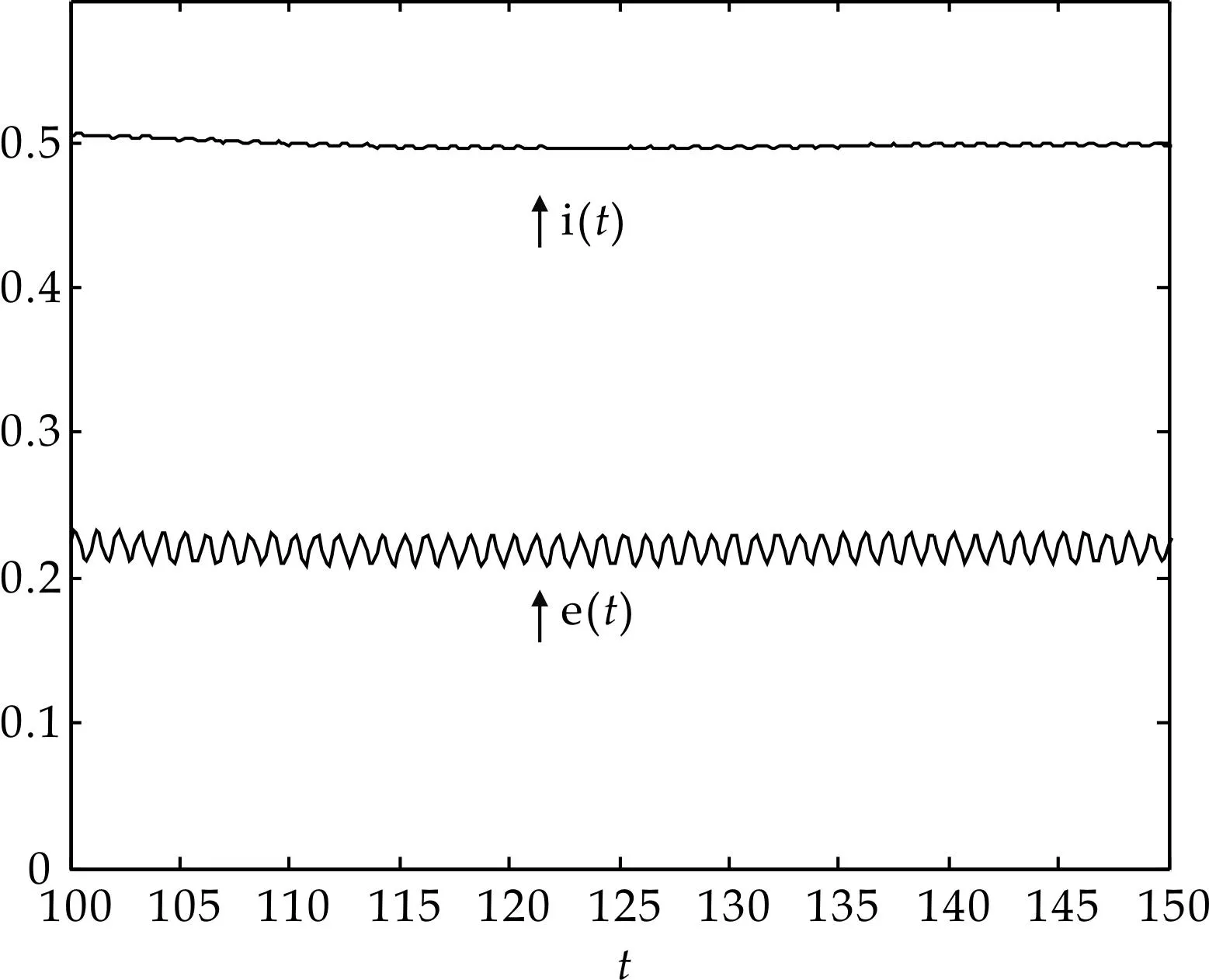
图2　疾病的一致持续

5结论

研究了一类具有周期双线性传染率的SVEIR模型的动力学性态. 利用积分算子的谱半径定义了模型的基本再生数，证明了无病周期解的全局稳定性，利用Poincaré映射半流讨论了系统的一致持续生存，并通过数值模拟验证了结论的正确性．我们的模型、方法和结论对周期传染病模型的应用及研究是一次成功的探索．

参考文献

[1] Keeling M,Rohani P.Modelling infectious disease in humans and animals[M].Princeton:Princeton University

Press,2008.

[2] Zhou Y C,Cao H.Discrete tuberculosis transmission models and their application[C]//A Survey of Mathematical Biology,Fields Communications Series,S.Sivaloganathan,eds.Canada:A Copublication of the AMS and Fields Institute,2010:83-112.

[3] 曹慧，王玉萍.具有饱和治愈率的离散SIS传染病模型的动力学性态[J].陕西科技大学学报(自然科学版),2013,31(5):147-150.

[4] Schwartz I B.Small amplitude,long periodic out breaks in seasonally driven epidemics[J].J.Math.Biol.,1992,30:473-491.

[5] Bacaer N.A pproximation of the basic reproduction numberfor vector-borne disease with a periodic vector population[J].Bull.Math.Biol,2007,69:1 067-1 091.

[6] Liu L,Zhao X Q,Zhou Y.A tuberculosis model with seasonality[J].Bull. Math.Biol.,2010,4:931-952.

[7] 杜鹏，段彩霞，廖新元.一类具logistic出生率的SIS传染病模型的全局稳定性[J].陕西科技大学学报(自然科学版),2014,32(4):167-171.

[8] Ma J.,Ma Z.Epdemic threshold conditions for seasonally forced SEIR models[J].Math.Biosci.Eng.,2006,3:161-172.

[9] 徐文雄,冯锋.潜伏期具传染力SEIS模型正平衡点的全局稳定性[J].数学的实践与认识，2012,42(9)：108-114.

[10] 原三领，韩丽涛，马知恩．一类潜伏期和染病期均传染的流行病模型[J].生物数学学报，2001，16(4)：392-398．

[11] Chen I J．Glogal stability of a SEIR epidemic model with nonmonotone incidence rate[J]．Journal of Biomathematics，2009，24(4)：59l-598．

[12] Z.Teng,L.Chen.Permanence and extinction of periodic predator-prey systems in a patchy environment with delay[J].Nonlinear Analysis:Real World Application,2003,4:335-364.

[13] T.Zhang,Z.Teng.On a nonautonomous SEIRS model in epidemiology[J].Bull.Math.Biol.,2007,69:2 537-2 559.

[14] Zhao X Q.Dynamical systems in population biology[M].New York:Springer-Verlag,2003.

[15] Wang W,Zhao X Q.Threshold dynamics for compartmental epidemic models in periodic environments[J].J.Dynam.Differential Equations,2008,3:699-717.

[16] Zhang F,Zhao X Q.A periodic epidemic model in a patchy environment[J].J.Math.Anal.Appl.,2007,325:496-516.

【责任编辑：蒋亚儒】

Analysis of a SVEIR epidemic model with periodic infection rate

DU Yan-fei, CAO Hui

(College of Science, Shaanxi University of Science & Technology， Xi′an 710021, China)

Abstract:A SVEIR epidemic model with periodic infection rate is formulated and studied.The basic reproduction number is defined,the global dynamics for disease-free periodic solution is estabished.The uniform persistence of system is also discussed.Numerical simulations are conducted to demonstrate our theoretical results and complex dynamics of the model.

Key words:periodic epidemic model; the basic reproduction number; stability

中图分类号：O175

文献标志码：A

文章编号：1000-5811(2016)01-0171-04

作者简介:杜燕飞(1984-)，女，浙江东阳人，讲师，硕士,研究方向：生物数学

基金项目：国家自然科学 (11301314)； 陕西省科技厅自然科学 (2014JQ1025)

收稿日期:*2015-11-16