一种考虑柔性的码垛机器人动力学性能优化方法

，，，

(哈尔滨工业大学机器人系统与国家重点实验室，黑龙江 哈尔滨 150000)

A Method for Dynamic Characteristics Optimization of Flexible Palletizing Robot

LIU Yanjie，MA Qingwu，LIANG Le，HAN Haijun

(State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150000, China)

一种考虑柔性的码垛机器人动力学性能优化方法

刘延杰，马清伍，梁乐，韩海军

(哈尔滨工业大学机器人系统与国家重点实验室，黑龙江 哈尔滨 150000)

A Method for Dynamic Characteristics Optimization of Flexible Palletizing Robot

LIU Yanjie，MA Qingwu，LIANG Le，HAN Haijun

(State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150000, China)

摘要：提出一种考虑关节柔性影响的高速重载码垛机器人动力学性能优化方法。首先，考虑关节柔性的影响，建立了刚柔耦合动力学方程；随后进行了模态分析以及受迫振动分析；提出以最低阶固有频率最大和各关节驱动力矩基于目标轨迹上的最大值最小作为动力学优化目标；最后构造有约束的多目标优化问题，并利用遗传算法对该多目标优化问题进行求解。优化结果表明，机器人的动力学性能明显改善，说明优化方法合理有效。

关键词：高速重载；柔性；动态特性；多目标优化

中图分类号：TP24

文献标识码：A

文章编号：1001-2257(2015)10-0057-05

收稿日期：2015-04-20

基金项目：国家“863计划”项目(2013AA040901)；黑龙江省创新专项(YC13D004)

Abstract：Considering the impact of flexible joint, a method for dynamics optimization design of high-speed, heavy-load palletizing robot is presented. Firstly, the flexible dynamics model is established and dynamics simulation is carried out. Next, Modal Analysis and forced vibration analysis is followed. The first natural frequency and the maximum joint driving torque based on the target trajectory are selected as dynamic optimization goals and a multi-objective optimization model is established, which is solved by NSGA-II genetic algorithm. Optimization results showed that: The dynamics performance of the robot is significantly improved, indicating that the optimization method is reasonable and effective.

作者简介：刘延杰(1975-)，男，教授，黑龙江哈尔滨人，研究方向为机器人技术;马清伍(1991-)，男，辽宁朝阳人，硕士研究生，研究方向为工业机器人结构优化。

Key words：high-speed and heavy-load; flexibility; dynamic characteristics; multi-objective optimization

0引言

随着高速重载码垛机器人在工业自动化生产线上的广泛应用，各种各样的生产需求对码垛机器人的各项性能提出了更高的要求。针对高速码垛机器人高速、高加速度、大负载的工作特性，仅仅在静力学层面上完成结构设计还不够，有必要对机器人本体进行面向动态特性的结构优化研究。

针对码垛机器人的动态优化设计，Khatib提出以机器人末端操作空间惯量特性为评价指标，给出了有效质量和有效转动的概念。Bowling和Khatib提出了一组机器人动态特性方程，可以统一描述机器人在操作空间中任意一点的速度、加速度和末端受力性能,并解决了指标中单位改变带来的不一致性问题。上述研究方法并未考虑关节柔性对于机器人动力学性能带来的影响，且上述研究是在给定机器人指定范围的前提下进行，没有考虑实际工况下的机器人运动情况，具有一定局限性。应考虑轨迹规划结果对机器人动力学性能带来的影响。

针对上述问题，从高速重载码垛机器人的工作特性出发，考虑关节柔性的影响，提出了一种高速重载码垛机器人动力学优化设计方法。首先建立了刚柔耦合动力学模型，并进行动力学仿真验证；然后进行了模态分析和受迫振动分析；完成了轨迹规划，以最低阶固有频率最大和基于目标轨迹上的峰值力矩最小为动力学优化指标，对高速重载码垛机器人进行了结构优化设计。对优化前后码垛机器人的各项性能进行了对比分析。

1刚柔耦合模型建立

1.1　机构原理

高速重载码垛机器人的双平行四边形机构如图1所示。其中主平行四边形确定末端点位置，辅助平行四边形使末端执行器与水平面保持一个固定的姿态。

图1　双平行四边形高速码垛机器人

驱动主平行四边形的电机被对称安装在转座上，分别驱动大臂和平行臂，对应关节转角为θ2，θ3；转座由腰部的电机驱动，对应关节角度为θ1。前3个关节确定末端点的位置，末端电机驱动转盘转动，转角记为θ4，用以对所操作工件进行旋转。整个机器人机构属于串并联混合机构。

1.2　刚柔耦合动力学建模

选取3个主动关节θ1，θ2，θ3作为广义坐标，采用拉格朗日第2类方程进行建模，最后可得机器人刚体动力学方程为：

(1)

其中惯量阵为：

(2)

由上式可以看出2、3轴惯量为常值；2、3轴与1轴间解耦，但2轴与3轴之间存在耦合关系。

机器人柔性关节等效原理如图2所示，即将减速机等效成了刚性减速机和柔性扭杆。电机输出力矩和角度分别为Tm和θm，机器人关节输出力矩和角度分别为Tl和θl，电机转子惯量为Jm，减速比为i，阻尼比为B，减速机刚度为K。

图2　柔性关节模型

可以推导出如下关系：

(3)

联立式(1)和式(3)，消去中间变量，得到最后的刚柔耦合模型：

(4)

2动态特性分析

作为高速、高精度机械重要的设计环节，动态特性分析的主要任务是对系统进行模态分析。其目的在于研究系统振动响应的规律，分析系统参数与动态响应之间的联系。

2.1　振动模态分析

根据多自由度系统模态理论，分析机器人的系统振动方程。考虑机器人在自由振动状态下，故外力矩T=0；重力项和阻尼项对模态影响很小，可忽略不计。根据刚柔耦合动力学模型，简化后的系统振动方程可写成：

(5)

系统固有频率可由式(7)求得：

(6)

机器人惯量矩阵是连杆转角的函数，说明低阶振动固有频率不仅与结构参数相关，同时也受关节转角θ2和θ3的影响，即机器人固有频率与其姿态有关。因此，在进行结构优化之前，有必要找到机器人空间振动频率最低的位置，重点针对此处进行动力学优化设计。图3为机器人最低阶振动频率同转角的关系图。

图3　一阶振动固有频率关节空间分布

从图3可以得出，机器人在θ1=0，θ2=0.1745，θ3=2.878姿态处固有频率最低，此处前三阶固有频率分别为f1=17.25 Hz，f2=21.0 HZ，f3=41.99 Hz。

2.2　强迫振动分析

利用 ADAMS 软件对码垛机器人进行激振测试，得出其各阶模态情况，通过仿真分析验证振动模态分析的正确性。

调节机器人位姿，使其处于上文得出的最低固有频率位姿处。采用单点激励的方法进行强迫振动分析，选取大臂端点为激励点，机器人末端为信号拾取点。可以得到末端合成位移的幅频特性如图4所示。

图4　机器人末端合成位移幅值

由末端点合成位移的幅频特性曲线可知，谐振峰值点对应的频率即为机器人的三阶模态频率。分别为f1=19.2 Hz，f2=23.2 Hz，f3=45.0 Hz，与之前振动模态分析的结果相近。

另外，受迫振动分析中，可以得到系统各阶模态频率比例幅频图，如图5所示。

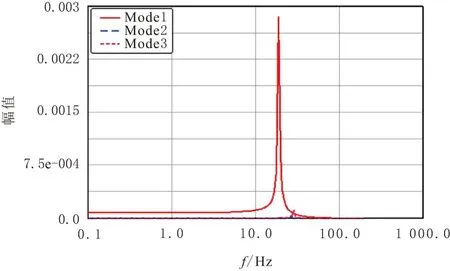
图5　系统各阶模态频率参与图

由图5可知，二阶和三阶模态频率的幅值比较小，即系统的后两阶模态对整个系统的参与因子较小。因此，对系统的动态特性优化重点针对最低阶固有频率。

3轨迹规划

考虑到进行优化设计时的动力学指标需要结合码垛机器人的具体工作情况提出，在这里有必要对码垛机器人进行必要的轨迹规划。

码垛机器人工作时，从传送带上抓取物料，沿运动路线将其放置在指定位置的动作循环。典型工作循环为负载抓起→负载腰转→负载堆垛→空载抬起→空载回转→空载下放。运动过程选用门字形运动轨迹运动，路径上各关键点坐标值(mm)如下: 物料抓取点P1(1 500,0,500)，运动路径转折点 P2(1 500,0,1 500) 及P3(1 500,1 800,1 500)，物料码放点 P4(1 500,1 800,500)。

机器人末端位置在4个点位间循环移动，6步动作间以停顿方式相互衔接。另外，如图 6所示间歇运动，解耦了大小臂关节组的运动与腰转关节运动。

图6　单工作循环各关节角速度

考虑到末端冲击对机器人造成的影响，如图7所示，采用弧线过渡模式，以减小因启停冲击带来的影响，同时也可缩短机器人运行周期，提高码垛效率。

图7　弧线过渡示意

4优化设计

4.1　设计变量

由双平行四边形码垛机器人结构特点可知，机器人特性主要由大臂、小臂以及平行臂杆长和截面积决定。为简化模型，将各杆件视为等截面杆件，选取大臂、小臂以及平行臂杆长和截面积作为设计变量。

4.2　动力学评价指标

最低振动固有频率的提高，能够有效提升系统动态特性，进行动力学优化设计，应将提高固有频率确定为首要优化目标。

为了提出机器人振动指标，首先推导出笛卡尔空间振动方程为：

(7)

J为雅克比矩阵。

定义Mc=J-TMJ-1为笛卡尔空间惯量矩阵，Kc=J-TKJ-1为笛卡尔空间刚度矩阵。则笛卡尔空间的动力学矩阵为Dc=Mc-1Kc，则振动指标为了使动力学矩阵的特征值γmin提高，即

(8)

关节驱动力矩峰值过大，不仅会增加能量损耗，同时会产生较大的力矩波动，从而降低机器人运行时的平稳性，会减小电动机的疲劳寿命。设法降低驱动力矩峰值对于提高机器人性能具有重要意义。因此，提出了峰值力矩指标，应当考虑选取大臂、小臂以及腰部的关节驱动力矩在门字形目标轨迹上的最大值和最小作为第2动力学性能优化目标，即

(9)

为了减少优化函数的数量，采用理想点法将3个力矩峰值的优化函数整理成单目标优化函数。理想点法的原理是选取各单目标优化后的目标函数值作为理想点，求出理想点后，在目标函数可行域内找到一点x*令其目标函数值F(x*)与理想点之间的距离最短。

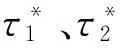
(10)

5算例

依据上述优化算法，通过工程实例来验证高速重载码垛机器人动力学优化方法的有效性。优化前高速重载码垛机器人主要结构物理参数定义及数值如表1所示。

表1主要物理参数定义

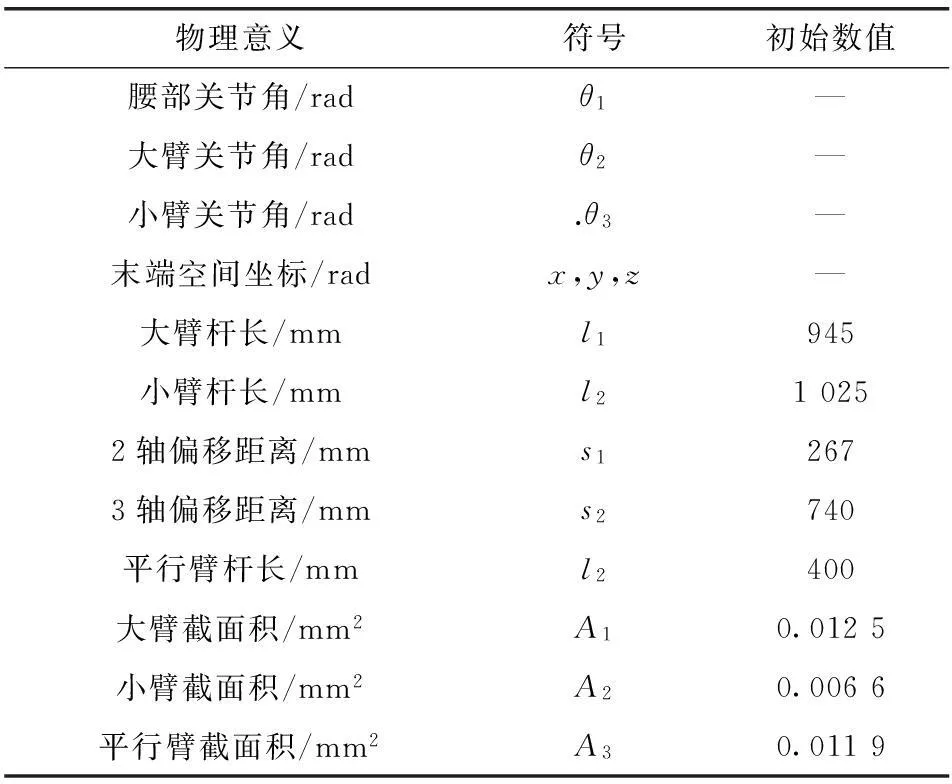
物理意义符号初始数值腰部关节角/radθ1—大臂关节角/radθ2—小臂关节角/rad.θ3—末端空间坐标/radx,y,z—大臂杆长/mml1945小臂杆长/mml210252轴偏移距离/mms12673轴偏移距离/mms2740平行臂杆长/mml2400大臂截面积/mm2A10.0125小臂截面积/mm2A20.0066平行臂截面积/mm2A30.0119

考虑到码垛机器人的结构和运动特点，可以得出其工作空间呈圆弧状分布。有必要建立工作空间约束条件，确保优化过后工作空间可以将所需的矩形空间包含在内。

优化后的机器人所达工作空间应满足以下需求：

(11)

对于多目标优化问题的求解，对遗传算法的研究最为丰富[4-]5]，选用了 NSGA-Ⅱ多目标遗传算法。NSGA-Ⅱ优化算法是对第1代 NSGA 算法的改进，在计算速度和效率上都有了提升。

以机器人原结构参数为初选参数。参数变化范围为±120%。设置种群大小Pop=30，遗传代数Gen=300。在遗传操作中，采用适应度值锦标赛竞争原则，交叉概率设为 0.8，变异概率设为 0.01。经过计算得到最优前沿面如图8所示。

图8　二目标函数空间Pareto最优前沿面

综合2个动态性能指标需求，最终确定Pareto解集第24组数据作为机器人结构优化结果，得到优化后的数据l1=0.862 8，l2=0.49，l3=0.975 7，A1=0.010 57，A2=0.016，A3=0.005 4。

优化前后各性能指标变化情况如表2所示。

表2优化前后性能指标对比

参数f1/Hzmin(τ)/N优化前数据17.252246.3优化后数据19.221937.1相对变化率11.4%-13.77%

上述数据为机器人在特定位姿下的固有频率性能情况。为了全面地表示优化前后的变化情况，采用工作空间下的等高线图来表示机器人的性能指标变化。

从图9和图10可以看出，优化后工作空间内的固有频率最小值超过了19 Hz，相对于优化前的17 Hz有了明显提升。优化后，大部分工作空间内的固有频率较优化前都有了提升，说明码垛机器人的动态特性得到的优化。

图9　优化前振动特性

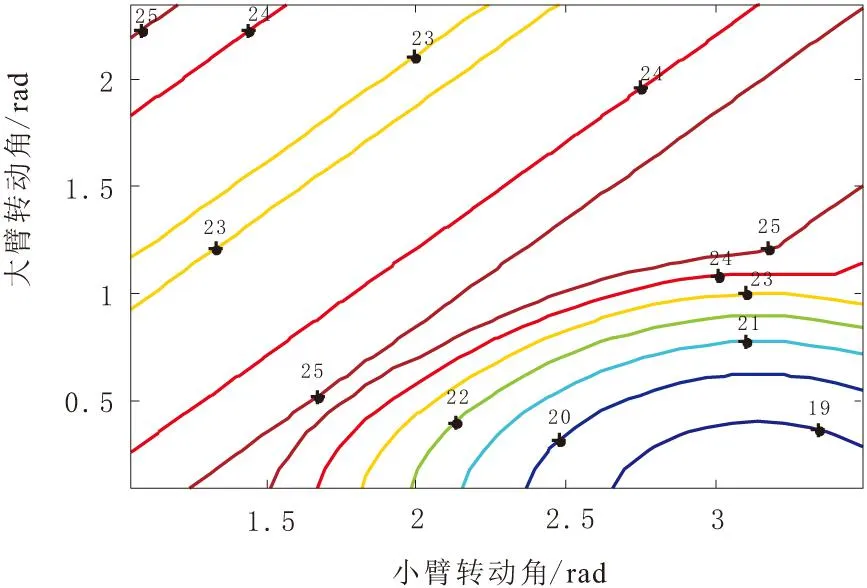
图10　优化前振动特性

6结束语

结合高速码垛机器人高速、高加速度、大负载的工作特性，考虑关节柔性的影响，提出了一种高速重载码垛机器人的动力学性能优化方法。首先建立了刚柔耦合动力学模型，运用Adams分析了关节柔性对系统的影响，并验证了动力学模型的正确性。然后进行了振动模态分析并进行了受迫振动仿真，验证了振动分析结果。进行了轨迹规划，提出了一种基于最低固有频率和力矩峰值为优化目标的动力学优化方法。利用该方法对高速重载码垛机器人进行了优化，优化结果表明，最低阶固有频率指标提升了11.4%，力矩峰值指标下降了13.7%，即该方法有效地提高了机器人的动力学性能。

参考文献：

LI Q，ZHANG W J，CHEN L.Design for control-A concurrent engineering approach for mechatronic systems design .Ieee-asme T Mech, 2001, 6(2):161-9.

KHATIB O.Inertial properties in robotic manipu lation:an object-level Framework .The International Journal of Robotics Research, 1995, 14(1):19-36.

BOWLING A, KHATIB O. The dynamic capability equations: a new tool for analyzing robotic manipulator performance . Robotics, IEEE Transactions on, 2005, 21(1): 115-23.

Sivanandam S N, Deepa S N. Introduction to genetic algorithms .Springer Publishing Company Incorporated, 2007.

Coello Coello C A. Evolutionary multi-objective optimization: a historical view of the field . Computational Intelligence Magazine, IEEE, 2006, 1(1): 28-36.

Saravanan R, Ramabalan S, Ebenezer N, et al.An evolutionary multi-criteria design optimization of robot grippers . Applied Soft Computing, 2009, 9(1):159-172.