外骨骼机器人系统中人体下肢关节力矩动态解算

，，，

(哈尔滨工业大学机器人技术与系统国家重点实验室 哈尔滨 150001)

Dynamic Solution of the Lower Extremity Joint Torques in Man-machineSystem of Lower Extremity Exoskeleton

GUO Wei，YANG Congwei，DENG Jing，ZHA Fusheng

(State Key Laboratory of Robotic and System，Harbin Institute of Technology，Harbin 150001，China)

外骨骼机器人系统中人体下肢关节力矩动态解算

郭伟，杨丛为，邓静，查富生

(哈尔滨工业大学机器人技术与系统国家重点实验室 哈尔滨 150001)

Dynamic Solution of the Lower Extremity Joint Torques in Man-machineSystem of Lower Extremity Exoskeleton

GUO Wei，YANG Congwei，DENG Jing，ZHA Fusheng

(State Key Laboratory of Robotic and System，Harbin Institute of Technology，Harbin 150001，China)

摘要：利用下肢外骨骼关节位移传感器及惯性导航单元采集人体运动信息，计算获得下肢髋、膝关节的相对角度以及躯干的姿态和加速度，通过动力学逆解实时解算穿戴者运动所需的关节驱动力矩。在此过程中，利用人体五杆模型，对人体下肢的运动进行了运动学和动力学分析，通过Matlab/Simulink软件编程求解，得到了人体下肢关节在连续步态周期内关节力矩的变化，通过对比计算获得的支撑踝关节力矩值与足底力传感器实测值，证明了关节力矩求解方法的正确性，保障了外骨骼机器人能够根据此力矩对穿戴者提供助力。

关键词：下肢外骨骼；关节力矩；动力学；Matlab/Simulink

中图分类号：TP242．3

文献标识码：A

文章编号：1001-2257(2015)10-0071-05

收稿日期：2015-05-21

Abstract：The method uses joint displacement sensors and inertial navigation unit on lower extremity exoskeleton to collect human motion information. Gets the relative angle of hip，knee and the posture and acceleration of torso. With inverse dynamics real-time calculating the joint driving torque of the wearers. In the procedure，with the 5-bar human model the kinematics and dynamics of human limb’s movement were analyzed. By Matlab / Simulink programming to obtain the curve of the joint torque of human lower limb joints in successive gait cycle. In order to prove the Correctness of the result，compare the joint torque of supporting leg ankle solved by lagrange dynamics equations with the ankle torque which was calculated by the plantar force measured during the experiment，the feasibility of the solving method was proved. Exoskeleton robot assiste the wearer with the torques information.

作者简介：郭伟(1965-)，女，黑龙江哈尔滨人，教授，研究方向为微小型及仿生足式机器人；杨丛为(1991-)，男，安徽涡阳人，硕士研究生，研究方向为外骨骼机器人。

Key words：lower extremity exoskeleton；joints torque；dynamics；Matlab/Simulink

0引言

目前，最具有代表性的外骨骼机器人是加州大学伯克利分校开发的下肢骨骼服BLEEX和日本筑波大学研发的HAL。

利用人体下肢关节力矩信息对不同环境中下肢的运动步态特征分析已见于诸多文献。郝智秀等通过求解下肢关节力矩分析了不同足地界面对三维步态特征的影响，张瑞红等对不同路况下步态特征进行研究，韩亚丽、王兴松对不同速度以及不同负重下人体下肢关节运动进行研究，以上研究表明，下肢关节力矩的变化体现出了丰富的人体运动步态特征信息，因此对人体下肢关节力矩的求解可作为获取穿戴者运动意图的一种途径。

在以往的研究中，研究者建立的是人机系统统一的动力学模型，对其求逆解作为关节目标驱动力矩，再根据穿戴者的生理信号，例如EMG、EFG等信号，对穿戴者的运动趋势做出预测，并没用利用人体下肢关节力矩直接作为运动意图感知的方式，然而受到EMG、EFG传感器的不稳定性影响，该方法的使用范围受到很大程度的限制。为了克服这种控制策略的局限性，提出一种基于人体下肢关节力矩求解与预测的人体运动意图感知的方法，在本文以实时获得人体下肢关节力矩为目标开展研究，为外骨骼的主动助力打下基础。

1模型的建立及关节坐标定义

人体下肢运动自由度包括大腿屈伸、外旋内旋、外展内收；小腿屈伸；足屈伸、外翻内翻，生物力学仿真及实验研究显示在人体矢状面内运动消耗的功率相对于额状面和水平面最大，因此可将对人的三维运动简化为较为简单的平面运动。五杆模型常用于对步行步态的运动学和动力学问题研究，其优点在于无需考虑其在额状面内侧向的步态稳定性。在模型中忽略了人的头部以及手臂在运动过程中的影响，将人体上半身简化为一根刚性杆件。每条腿被简化为通过与矢状面垂直的铰链关节相连接的两根刚性杆件，并将足与小腿固连，假设在步行过程中模型仅仅通过小腿刚性杆件的端部与地面接触。

将人体简化为五杆模型后，即可将人体各环节视为刚体杆件处理，要对人体的运动进行分析，需要确定各杆件的位姿，为了定义各杆件的位姿，先要确定各杆件的局部坐标系，并通过坐标系描述各杆件的几何关系，人体环节的局部坐标系定义如图1所示。

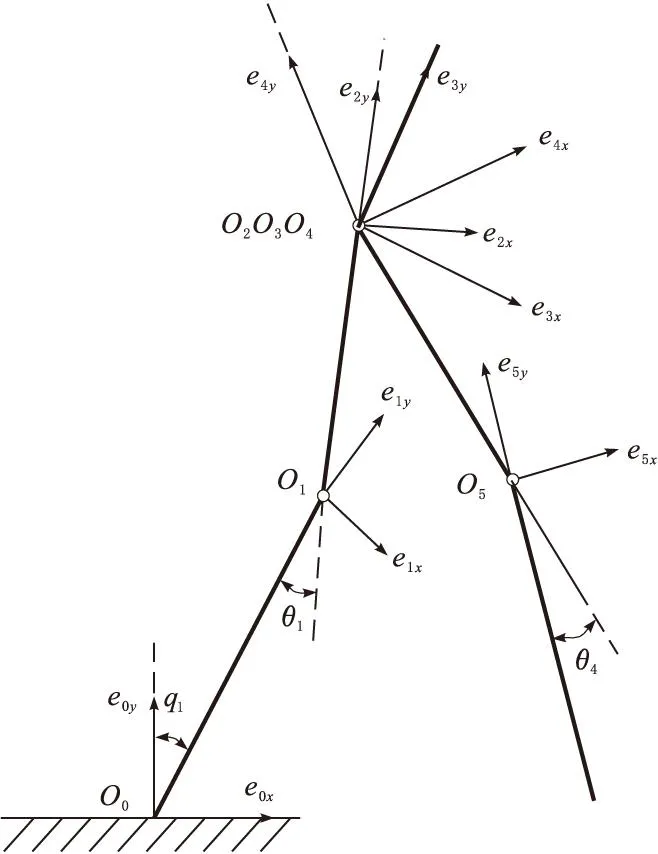
图1　坐标系建立

牵连坐标系定义在支撑腿脚跟着地处，e0x与脚面平行，从踝关节指向脚尖，e0y垂直于脚面。牵连坐标系确定人体在平面中的位置，但不能表征人体姿态，而其他局部坐标系则用于确定人体位姿。

所有局部坐标系的X轴均垂直所在环节，指向运动的正前方。

2人体特征参数与运动学分析

2.1　特征参数获取

由于每个穿戴者下肢和躯干的几何参数及惯性参数难以直接测量，但是这些参数符合统计学规律，可使用回归方程并根据使用的身高、体重计算人体环节的各几何参数及惯性参数值。

参考文献中给出了计算中国成男性人体惯性参数的回归方程系数，可建立如式(1)所示的回归方程，据此编写求解五杆模型中躯干、左右大腿、左右小腿的质量、质心位置及通过质心位置在额状面的转动惯量的归一化函数，函数中，将人的头部、左右手臂的质量归入到躯干中，此时，躯干的质心位置由质心式(2)计算、过新质心的转动惯量由平行轴定理式(3)计算，足的质量并入小腿，小腿杆的质心位置亦按式(2)计算，将足的转动惯量忽略。实验时只需输入外骨骼穿戴者的身高、体重、躯干长、大腿长等可直接测量的信息，即可获得五杆模型中杆件的特征参数。

Y=B0+B1X1+B2X2+B3X3+…

(1)

(2)

(3)

Jn为新位置处的转动惯量，Jyi为原环节对其质心的转动惯量，mi为原环节的质量，di为原环节的质心到新质心的距离。

例如穿戴者的身高为1.720m，体重为70kg时，求得的特征参数如表1所示。

表1五杆模型中的特征参数

特征环 节躯 干左右大腿左右小腿质量/kg39.19659.66475.6681质心位置/m0.21910.23640.2149惯量/kg·m27.70580.13630.0178

其中，躯干的质心位置起测点为五杆模型中躯干杆的最低点；左右大腿的质心位置起测点为相应的膝关节处；左右小腿的质心位置起测点为相应的踝关节处。

2.2　人体关节角度定义

为了准确的求解人体运动时的关节力矩，需要对人体运动时的关节角度进行合适的定义，避免在双腿支撑相与摆动相交替时出现混乱。相邻两杆件间的相对角度为关节相对角度，用θ1～θ4表示；θ1为支撑腿膝关节角度；θ2为支撑脚髋关节角度；θ3为摆动腿膝关节角度；θ4为摆动腿髋关节角度。

杆件与竖直方向的夹角为杆件的绝对角度，用q1～q5表示；q1为支撑腿小腿的绝对角度；q2为支撑腿大腿的绝对角度；q3为上肢绝对角度；q4为摆动腿大腿绝对角度；q5为摆动腿小腿的绝对角度。绝对角度及相对角度定义如图2所示。

图2　关节角度定义

关节相对角度，能够直接表征关节转动角度的大小，可用外骨骼上的角度传感器直接测量得出，而绝对角度方便描述人体上重要点的运动学空间坐标，但绝对角度不是都能测量得到，只有固定了惯性导航器件的躯干，可以获得上肢杆件的相对地面的姿态信息及加速度变化，其他杆件的绝对角度，可以用1个上肢姿态和4个相对角度求解得到。

绝对角度和相对角度向量为：

(4)

2个向量空间满足关系为：

(5)

(6)

外骨骼具有和穿戴者相同的运动轨迹，由外骨骼上的传感器可获取的人体的运动信息。如图3所示为平地行走过程中的上肢绝对角度信息，各关节相对角度如图4所示。

图3　躯干绝对角度

图4　髋关节、膝关节相对角度

由图3可以看出，平地行走过程中躯干相对竖直方向的角度变化较小，在±2°的范围内变化，这是人体行走时躯干的正常摆动，其中正值代表躯干前倾，负值代表躯干后仰。由图4可知，髋关节的角度范围在-10°～20°的变化，当大腿前屈了为正角，后伸时为负角；膝关节的运动范围在-50°～0°，当小腿与大腿在同一直线时为0°。这些角度的变化均在正常的关节角度范围内，且符合人在平地行走时关节角度的变化规律。

3动力学模型建立及实时求解过程

3.1　动力学模型

多刚体系统的动力学求解方法主要有拉格朗日法和牛顿-欧拉法。拉格朗日法是根据全部杆件的动能和势能求出拉格朗日函数，导出刚体各杆件的运动方程。这种方法只需速度而不必求各杆件的内作用力，直接求出关节的驱动力矩，是一种比较清晰简便的方法。牛顿-欧拉法在运用时需要求解杆件之间的内力，并消去内力，对于较复杂的系统，此种分析方法十分复杂和麻烦。

主要研究五杆模型的动力学逆解，即给出各关节的位移、速度、加速度，求解关节驱动力(驱动力矩)，可表示为式(7)。针对单腿支撑相建立模型进行分析，五杆模型中每根杆具有3个自由度，可以理解为杆件质心在平面内的运动以及杆件绕质心的转动，根据杆件之间的连接关系，可确定在单腿支撑相，五杆模型系统具有7个自由度，在双腿支撑相具有5个自由度。模型相对复杂，因此选择使用拉格郎日法处理动力学问题。

(7)

在利用拉格朗日函数建立动力学模型时，需要定义系统的广义坐标，由于主要的求解目标是关节力矩，因此考虑选用4个关节间的相对角度、支撑相小腿的绝对角度，以及支撑脚的位置坐标作为广义坐标。摆动腿的踝关节作为一个随动关节，足部质量已算入小腿杆。在求解时用绝对角度去求解环节质心位置的坐标更加方便，绝对角度描述人体环节质心的运动学空间坐标。

在单腿支撑相中，质心位置为：

(8)

lj为杆件长度，di为杆件质心长度。

势能为：

(9)

动能为：

(10)

拉格朗日函数为：

L=K-P

(11)

则，各关节广义力矩为：

(12)

求解时，使用相对角度表示绝对角度，则可直接求出下肢关节力矩。

3.2　Matlab/Simulink关节力矩求解

完成动力学模型的建立后，利用Matlab软件对关节力矩进行求解，而以往的动力学模型中使用绝对角度进行求解，求得的结果并不是关节力矩，仍需根据牛顿第三定律进一步求解，在编程时，用相对角度表达绝对角度，求得拉氏函数后对相对角度求微分(偏微分)，可直接得到人体髋关节、膝关节力矩。

考虑到实际外骨骼机器人系统中，7个广义坐标中的支撑相小腿的绝对角度以及支撑脚的位置坐标，均是无法测量得到的，而这3个量可以由位于背部的惯性导航器件测量得出的量，即由人体上肢的倾斜角度、背部的绝对位置坐标，结合相对角度和人体尺寸进一步推导，由几何关系计算得到。

由式(8)、(9)、(10)可推导出由相对角度表示人体环节质心位置表达式(8)，质心水平坐标表达式对广义坐标求解雅克比矩阵，如式(13)所示，故人体环节在笛卡尔坐标系下各环节质心速度计算如式(14)。推导出环节质心的速度公式后，即可计算出系统的动能、势能，进而得出拉格朗日函数。

(13)

(14)

由式(12)，分别求拉氏函数对广义坐标、广义速度的雅可比矩阵，得到下肢关节力矩关于广义坐标及其一二阶倒数的函数表达式。再Matlab/Simulink仿真求解部分包含三部分内容，分别完成支撑腿判断、广义坐标值确定、拉格朗日动力学求解功能。

4结果验证与分析

关节力矩求解的结果如图5所示。

图5　关节力矩求解结果

通过图5可以看出，求解出的踝关节力矩的峰值最大(-150 N·m)，出现在支撑相末期，在摆动时，踝关节力矩很小。髋关节和膝关节的力矩峰值均约为80 N·m。可以发现，左腿和右腿的力矩具有相同的变化趋势，但有相位差，该变化趋势也符合人体运动的规律[10]，因此该结果可取，为进一步验证结果的正确性，将利用拉格朗日动力学方程求解出的支撑腿脚踝处在支撑时的关节力矩的变化与实验时用力台测取的足底力计算出的踝关节力矩对比，如图6所示，二者具有相同的变化趋势，并且大小相差在一定的误差范围，证明了求解过程的正确性，由于关节力矩是由统一拉格朗日能量函数对广义坐标及广义坐标的一阶导求偏微分运算得出，广义坐标作为系统的输入已在前文说明其正确性，因此当支撑踝关节的力矩求解正确时，其他关节的力矩亦可视为正确解。

图6　支撑踝关节力矩对比

5结束语

解决了下肢外骨骼人机系统中，动态求解人体下肢关节力矩的问题，利用人体五杆模型，建立拉格朗日动力学方程求解出人体下肢的关节力矩在连续周期的变化，将利用拉格朗日动力学方程求解出的支撑腿脚踝处在支撑时的关节力矩的变化与实验时用力台测取的足底力计算出的踝关节力矩对比，验证求解过程的正确性。与以往的研究相比，使用关节相对角度求解关节力矩，可直接得到人体下肢关节力矩；利用下肢外骨骼系统对人体下肢关节力矩进行动态求解，为外骨骼机器人获取人体运动意图提供了一种方法。

顾文锦，朱宇光，杨智勇，等. 下肢骨骼服全过程运动控制研究. 控制工程，2011，18(2)：290-293.

郝智秀，周吉彬，金德闻，等. 不同足地界面对人体三维步态的影响. 清华大学学报(自然科学版)，2006，46(8)：1388-1392.

张瑞红，金德闻，张济川，等. 不同路况下正常步态特征研究. 清华大学学报(自然科学版)，2000，40(8)：77-80.

韩亚丽，王兴松. 人体行走下肢生物力学研究.中国科学(科学技术)，2011，41(5)：592-601.

张佳帆，陈鹰，杨灿军. 柔性外骨骼人机智能系统. 北京：科学出版社，2011.

柴虎. 下肢外骨骼机器人跟随系统的研究. 广州：南方医科大学，2013.

Racine J L.Control of a lower extremity exoskeleton for human performance amplification .Berkeley：University of California，Berkeley，2003.

刘静民. 中国成年人人体惯性参数国家标准的制定 . 北京：北京体育大学，2004.

蔡自兴. 机器人学. 北京：清华大学出版社，2009.

[10]Andrew Chu，Kazerooni H，Adam Zoss. On the biomimetic design of the berkeley lower extremity exoskeleton (BLEEX)//International Conference on Robotics and Automation，Barcelona，Spain，2005.