四旋翼两栖机器人姿态求解与控制

，，，，，，3，，

(1.中国科学院合肥物质科学研究院先进制造技术研究所，江苏 常州 213164；

2．电子科技大学自动化系，四川 成都 611731；3. 中国科学技术大学自动化系，安徽 合肥 230027)

Attitude Solving and Control of an Amphibious Robot Based on Four-rotor

LI Tao1，WEI Qiang2，FU Long1，LUO Minzhou1，CHEN Saixuan1，WANG Meiling1，3，LIU Xiao1，ZHUANG Xiaoming1

(1．Institute of Advanced Manufacturing Technology，Hefei Institute of Physical Science CAS，Changzhou 213164，China；

2．Department of Automation of University of Electronic Science and Technology of China，Chengdu 611731，China；

3. Department of Automation of University of Science and Technology of China，Hefei 230026，China)

四旋翼两栖机器人姿态求解与控制

李涛1，魏强2，付龙1，骆敏舟1，陈赛旋1，王美玲1，3，刘效1，庄晓明1

(1.中国科学院合肥物质科学研究院先进制造技术研究所，江苏 常州 213164；

2．电子科技大学自动化系，四川 成都 611731；3. 中国科学技术大学自动化系，安徽 合肥 230027)

Attitude Solving and Control of an Amphibious Robot Based on Four-rotor

LI Tao1，WEI Qiang2，FU Long1，LUO Minzhou1，CHEN Saixuan1，WANG Meiling1，3，LIU Xiao1，ZHUANG Xiaoming1

(1．Institute of Advanced Manufacturing Technology，Hefei Institute of Physical Science CAS，Changzhou 213164，China；

2．Department of Automation of University of Electronic Science and Technology of China，Chengdu 611731，China；

3. Department of Automation of University of Science and Technology of China，Hefei 230026，China)

摘要：介绍了一种基于四旋翼驱动的两栖移动机器人。首先简要介绍了该机器人的机械结构与控制及传感系统，并介绍了机器人由四旋翼机构提供动力，并通过对4个旋翼的转动速度和方向进行配置，从而实现在空中飞行或在地面滚动的原理。然后，采用四元数方法对该两栖机器人进行了姿态求解，在此基础上，基于PID算法开发了机器人的飞行控制算法，并进行了相应的仿真。最后通过实验验证了该两栖机器人能够实现预期的两种运动模式，即空中飞行和地面滚动。该机器人提高了传统只具有单一运动模式的移动机器人的环境适应能力。

关键词：移动机器人；四旋翼机构；两栖机器人；姿态求解；运动控制

中图分类号：TP242

文献标识码：A

文章编号：1001-2257(2015)10-0062-05

收稿日期：2015-06-16

基金项目：中国科学院合肥物质科学研究院院长基金青年火花项目(YZJJ201323)

Abstract：This paper mainly introduces the attitude solving and control of an amphibious robot based on four-rotor mechanism. Firstly，it introduces the mechanism，control and sensor system，then it introduces the working principle that four-rotor works as actuator，and by configuring rotating velocity and direction of the four rotors，the robot can both fly in the air and rolling on the ground. Then，the attitude solving is carried out by using quaternion method，and then control algorithm is developed as based on PID algorithm，after then corresponding simulation is implemented. Finally，experiments are presented to verify that the robot can generate two motion modes，namely flying in the air and rolling on the ground，as expected. This amphibious robot enhances the environment adaptability of conventional mobile robots which just have a single motion mode.

作者简介：李涛(1984-)，男，安徽霍邱人，助理研究员，博士，研究方向为服务机器人；魏强(1992-)，男，安徽霍邱人，硕士研究生，研究方向为服务机器人。

Key words：mobile robot；four-rotor mechanism；amphibious robot；attitude solving；motion control

0引言

现有的移动机器人移动方式各异，常见的有轮式、腿式、蠕动及飞行等方式[1-]5]，它们的运动性能各有优点，但也存在着不足，主要表现在环境适应的局限性。受运动方式的限制，目前研制出的基于这些运动方式的移动机器人大多只适用于单一作业环境，即或地面、或水下、或空中。近年来也出现了少量的两栖机器人，如水陆两栖机器人[6-]7]，是以两栖动物蛇为仿生对象开发的机器人。

介绍了一种基于四旋翼的两栖机器人，通过创新机构设计，将四旋翼机构与柔性球壳机构集成到一起，该机器人既可以实现空中飞行，又可以实现地面滚动，且两种运动模式共用一套驱动系统。此外，当机器人在两种运动模式间来回切换时，在柔性球壳机构的保护下，可以有效地避免机器人因撞击而导致的损坏。

1机器人系统设计

机器人机械结构如图1所示，主要由四旋翼机构和柔性球壳机构耦合而成。四旋翼机构是机器人的动力来源，而球壳机构的作用是当机器人在空中飞行时作为保护装置，而在地面滚动时，球壳机构即作为保护装置又作为运动装置。四旋翼机构与球壳机构之间通过轴承连接，从而使得旋翼机构可以绕长轴相对于球壳机构进行转动。该四旋翼两栖机器人可以实现空中飞行和地面滚动两种运动方式，两种运动方式均由四旋翼提供动力，通过配置各旋翼的转速及转向，可以实现机器人在空中的上下、前后、左右飞行、侧向飞行及悬停等，也可以实现机器人在地面上的前后滚动及转向。

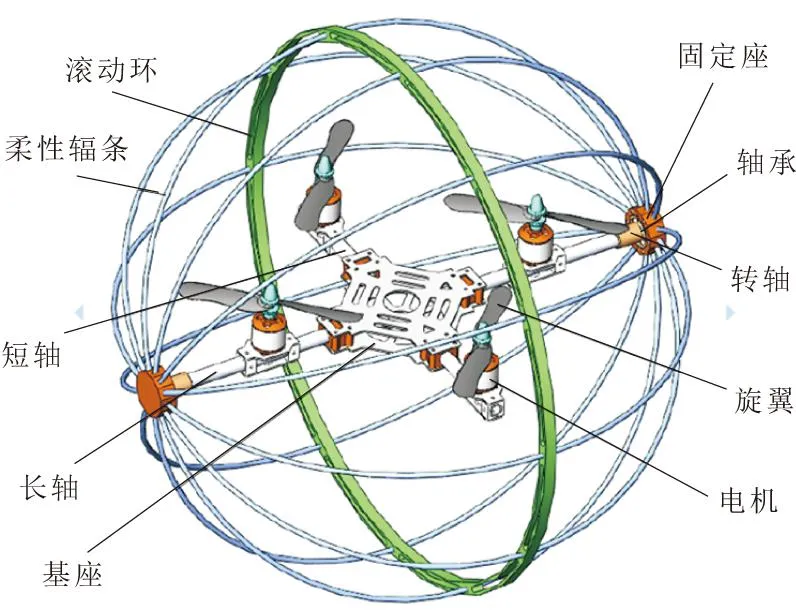
图1　机器人机械结构

两栖机器人是由旋翼提供的升力完成各项目标运动，依赖于对自身状态及旋翼的快速响应保持机身系统的稳定。两栖机器人的硬件系统主要包括飞行控制系统、导航系统、电源及动力系统、遥控及无线通信模块以及其他任务设备，两栖机器人控制系统的硬件结构如图2所示。其中飞行控制系统是整个系统的核心，用于收集传感器信息，解算飞行姿态输出PWM波，接收遥控信号及返回飞行信息等，导航系统用于采集飞行信息，将飞行信息上传到控制模块中，电源及动力系统为整个系统供电及为机体的飞行提供升力，遥控通过接收机向控制系统发送PPM信号，用于控制机器人的升降及调整机器人的飞行姿态，无线通信模块用于机器人返回飞行信息，监测机器人的飞行状态。其他任务设备可能含有摄像机等，用于机器人执行其他需要的任务。

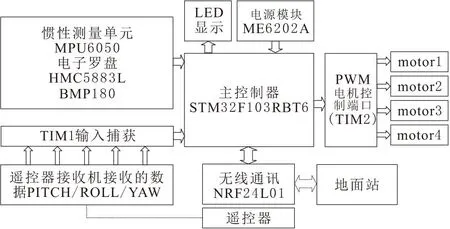
图2　两栖机器人控制系统的硬件结构

2机器人姿态求解

在四旋翼的导航系统中，首先设导航坐标系为OnXnYnZn，为了确定飞行器的导航参数并对其的位姿信息进行数学描述，采用载体坐标系ObXbYbZb，即在四旋翼上机器人上建立坐标系，原点选在四旋翼的中心，X轴沿四旋翼纵轴向前，Y轴沿四旋翼横轴向左，Z轴垂直于机体向上。设载体坐标系在初始时刻与导航坐标系重合，载体坐标系经过偏航方向、俯仰方向、横滚方向上3个角度的旋转后得到新的载体坐标系Ob′Xb′Yb′Zb′。

2.1　姿态角

设在某一坐标系下存在一向量R，用范数为1的四元数Q描述该坐标系的旋转R′，则有：

(1)

设有2个四元数A和B，其中A=a0+a1i+a2j+a3k，B=b0+b1i+b2j+b3k，设C=c0+c1i+c2j+c3k为A和B两四元数的乘积，即C= A·B，则有：

(2)

设Q=q0+q1i+q2j+q3k，且设

(3)

可由四元数得出姿态矩阵：

(4)

则可得姿态角：

(5)

对于任意旋转，可用一单位四元数Q=cos(θ/2)+ usin(θ/2)表示，其中u为单位向量。用Q描述导航坐标系到载体坐标系的旋转，则w=wg=QwbQ*，其中wg，wb分别为角速度在导航坐标系和载体坐标系的表述。因为Q为单位四元数，即Q·Q*=Q*·Q=1，所以有：

(6)

将上面的微分方程离散化便可由初始时刻四元数的值及各时刻的三轴角速率获得接下来各个时刻的四元数的值，便可由四元数矩阵获得当前的载体姿态。

2.2　基于陀螺仪、加速度计、磁力计的姿态求解

两栖机器人配备了陀螺仪、加速度计和磁力计。通过陀螺仪得出3个轴上的角速度wb=[wbxwbywbz]，使用式(6)的离散形式由初始四元数不断以角速度矩阵更新得出实时的四元数，再由式(5)便可求出当前载体的姿态角。需要说明的是单纯使用加速度计无法提取到偏航方向的角度，而磁力计的引入则能解出偏航方向的角度变化。由于单个磁力计在测量过程中存在着误差，故使用多传感器进行姿态融合，得到较为精确的姿态数据。基于PI调节的姿态融合的基本思想为以陀螺仪的数据不断累加解出当前姿态矩阵为基础，以加速度计与磁力计作为反馈，通过姿态矩阵得出理想输出并与实际输出的向量积作为误差，通过PI调节加至陀螺仪的累加过程中进行数据融合不断更新四元数。将导航坐标系的理论加速度向量[00g]经过四元数旋转矩阵转换至载体坐标系上，利用载体上加速度计实际的输出值与转换后的理论值做向量积误差输入到PI控制器上，经过PI控制器补偿到陀螺仪上。

使用上述方法得出的解出的静态漂移的姿态角如图3所示。从图中可以看出基于上述方法解算出的姿态角静态精度为0.2°且解算速度可以达到2 ms一次，能够满足飞行器的飞行要求。四旋翼飞行器是一个强耦合、欠驱动、非线性的控制系统，对其进行有效准确且稳定的控制是四旋翼飞行器设计中一个很大的难点。虽然四旋翼飞行器有4个电机输入，但是却要控制6个自由度的输出，分别为平移的3个自由度和旋转3个自由度，再加上四旋翼飞行过程中旋翼间存在相互影响和干扰就造成了四旋翼在控制上具有强耦合、非线性等的特点。本章将简单介绍应用于四旋翼上的控制方法，并基于以上建立的简化模型进行控制仿真和软件设计。

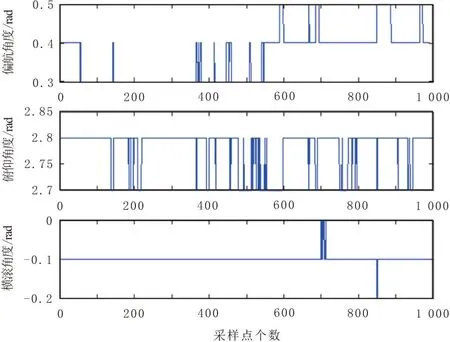
图3　静态漂移的姿态角

3机器人姿态控制

控制模型的不确定性以及存在的外界干扰等都会增加姿态控制的复杂度。该机器人应用了经典的PID控制策略，该种控制方法的控制结构较为简单，适应性强，鲁棒性好，且不需要预先知道被控对象的确切模型，也能达到较好的控制效果。在以上建立的动力学模型及PID控制的基础上，将四旋翼飞行器的控制算法分成两个回路，即为姿态控制回路与位置控制回路，四旋翼控制模型如图4所示。

图4　四旋翼控制模型

姿态回路是四旋翼能够稳定飞行的基本回路，其是位置控制回路的控制前提，决定了飞行器的控制品质，其具体作用为控制飞行器的飞行姿态，使各姿态角与设定的姿态角一致。姿态控制回路有3个控制量分别为俯仰角φ、横滚角θ、偏航角ψ，忽略各个姿态角间的耦合关系，对3个角分别进行独立的PID控制。

由上面推导得姿态的动力学模型为：

(7)

由动力学方程的推导得，u2，u3，u4与电机转速的平方成正比，分别以u2，u3，u4为控制量，则其有如下的控制形式：

(8)

由控制方程与系统的动力学模型对姿态环进行Simulink仿真，仿真参数如下：Iφ=Iθ=0.004 9 kg·m2，Iψ=0.008 8 kg·m2。因为在四旋翼的稳定飞行过程中不可能存在着很大的横滚角和俯仰角的变化，因此该仿真是在机体小角度旋转下进行的，横滚角的仿真结果如图5所示。此时通道的比例增益为3，积分增益为0.08，微分增益为2。仿真设计的阶跃的稳定值为0.1 rad，换成角度值约为6°，由图中可以看出，仿真的超调量小于0.05 rad，转换成角度值小于3°，满足四旋翼小角度变化的要求。虽然仿真中在0.08 s左右才达到预定值0.1 rad，但是可以看出由于Y轴的变化范围较小，在远小于0.08 s的时间内角度的调节就已经达到了可接受的范围内，即可视为稳定。

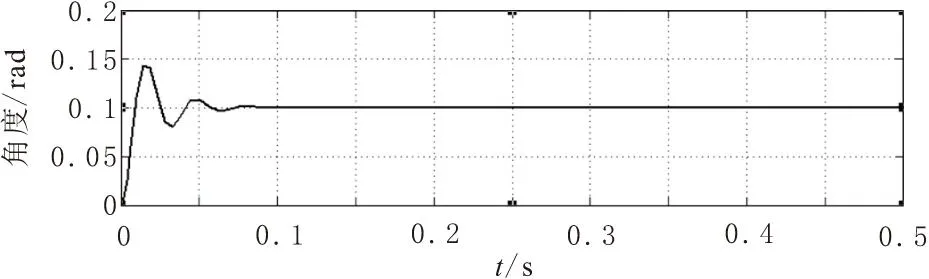
图5　横滚角的仿真结果

俯仰角的仿真结果如图6所示。同横滚通道一样，俯仰通道的比例增益为3，积分增益为0.08，微分增益为2。得出的仿真结果与横滚角的仿真结果类似，说明了四旋翼的结构具有对称性。

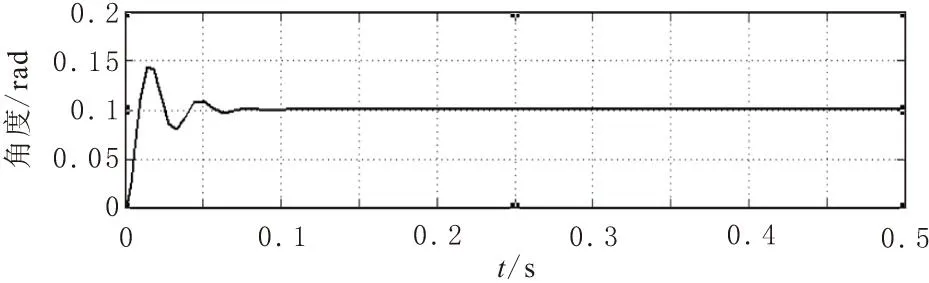
图6　俯仰角的仿真结果

偏航角的仿真结果如图7所示。仿真偏航通道时的比例增益为5.8，积分增益为0.05，微分增益为2.5。其角度的单位也为弧度制，超调量小于3°，调节时间小于0.05 s，满足四旋翼的飞行要求。

图7　偏航角的仿真结果

在做姿态环仿真的同时通过Z轴的动力学方程还对机体的高度进行了控制，仿真结果如图8所示。图中给定值为10 m，可以看出超调量小于2 m，调节时间约为2 s，仿真的结果在实际飞行中可以接受。

图8　Z轴高度仿真结果

4实验验证

在理论分析与机器人系统设计的基础上，加工制作了实验样机，并进行了实验。实验包括两部分，一部分为机器人的飞行测试，主要针对四旋翼机器人在室外的平稳飞行，自主起飞进行试验，以证明机器人能够实现前文中所述的姿态控制，即悬停、上升、下降、前进、后退、左右侧飞以及滚转等；另一部分为机器人的地面滚动测试，主要是验证机器人能够实现在指定的起始点与目标点间做可控的来回滚动以及转向的试验。通过以上两部分的测试来验证机器人分析和设计的有效性及合理性。

图9为四旋翼在室外进行的飞行试验，机器人可以保持较为平稳的飞行姿态。试验时发现当油门信号较小时，机体会存在些许振荡，需要一定时间才能平稳下来，当油门信号较大时，机体能够在很短的时间内稳定下来。综合飞行可能室外环境存在风力等的干扰，当机体油门信号较小时由于调节的力度不够大使得机体稳定需要较长的时间，当油门信号较大时由于调节力较大可以很快使得机体稳定。此外，在室外飞行测试过程中还对四旋翼机器人外壳的保护作用进行了测试，测试过程中，在10 m左右的高度下人为使机器人失去控制信号从而模拟意外掉落，当机器人撞击地面时，由于弹性球壳机构的保护作用，机器人从地面小幅弹起几次而并没有损坏，证明了外壳的设计起到了预期的保护作用。

图9　四旋翼室外飞行试验

两栖机器人滚动试验如图10所示。试验中，事先给定机器人的运动的起点A、中转点B和终点C，然后发送控制命令使机器人先从A点滚动到B点，再由B点滚动到C点。实现了该机器人在地面上朝着目标点的前进和后退滚动，同时实现了转向运动，从而验证了机器人结构设计的合理性。

图10　机器人的地面滚动试验

5结束语

介绍了一种既可以实现空中飞行又能够实现地面滚动的两栖移动机器人，通过将四旋翼机构和柔性球壳机构有效耦合，实现了通过四旋翼对两种运动模式的驱动。在姿态角求解和姿态控制的基础上，通过开发试验样机进行试验，改进了设计中存在的不足，实现了对机器人的有效控制，实现了预计的功能。该两栖机器人改进了传统只具备单一运动模式的移动机器人的环境适应性。

参考文献：

Ziv N，Lee Y，Ciaravella G. Inline skating motion generator with passive wheels for small size humanoid robots // 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics Montréal，Canada，2010：1391-1395.

王扬威，王振龙，李健. 仿生机器鱼研究进展及发展趋势.机械设计与研究，2011(02)：22-25.

Hashimoto K，Hosobata K，Sugahara Y，et al. Realization by Biped Leg-wheeled Robot of Biped Walking and Wheel-driven Locomotion //International Conference on Robotics and Automation，Barcelona，Spain，2006：2970-22975.

Carbone G，Suciu M，Ceccarelli M,et al. Design and simulation of Cassino hexapode walking machine . International Journal of Mechanics and Control，2009，10(2)：27-34.

侯宇，方宗德，孔建益，等.仿生扑翼飞行微机器人研究现状与关键技术. 机械设计，2008，25(7)：1-4.

蔡舒文，饶进军，肖辅龙.仿蜥蜴水面机器人脚掌设计.机械设计与研究，2012，28(1)：22-25.

Tesch M，Lipkin K，Brown I. Parameterized and scripted gaits for modular snake robots . Advanced Robotics，2009，23(9)：1131-1158.