基于SST湍流模型的圆盘空化器超空泡特性仿真分析
基于SST湍流模型的圆盘空化器超空泡特性仿真分析
侯保新,支希哲,刘永寿,刘伟
(西北工业大学力学与土木建筑学院,陕西西安710129)
摘要:基于全空化模型和SST k-ω湍流模型,对圆盘空化器的空化流动进行了仿真。首先,分析了平头回转体表面的压力分布,所得结果与Rouse和McNown的试验结果符合良好,验证了文中数值方法的有效性。其次,计算得到了不同空化数下无攻角圆盘空化器的超空泡形态特性和阻力特性,并与经验公式进行比较,二者具有良好的一致性。最后,对带攻角圆盘空化器进行了仿真,分析了攻角对超空泡形态特性和流体动力特性的影响。研究表明空化数和攻角都对超空泡的主要尺寸有影响,而攻角还会对超空泡的对称性和回射流现象产生显著的影响,此外攻角对圆盘空化器的流体动力特性也有比较大的影响,尤其是对升力系数有着直接的影响。研究结果为圆盘空化器在水下航行体上的应用提供了参考。
关键词:SST湍流模型;超空泡形态;流体动力;空化数;攻角
水下航行体在水中运动时,其阻力远大于在空气中运动时的阻力,且其阻力与速度的平方成正比,因此用常规方法难以有效提升水下航行体的速度[1]。超空泡技术是一种革命性的减阻方法,可使运动阻力减少90%,从而实现水下航行体的超高速飞行[2]。基于超空泡技术,俄罗斯研制了“暴风”超空泡鱼雷,其速度可以达到100 m/s,而美国实施了机载快速灭雷系统,并通过实验研究证实可以使超空泡射弹的速度达到1 000 m/s的量级[3]。
成功利用超空泡技术的关键是使航行体周围产生稳定可控的超空泡。位于航行体头部的空化器是诱导产生超空泡的关键部件,其形状和尺寸不仅决定了超空泡产生的难易程度,还决定了超空泡的形态。同时由于空化器是和水接触的主要部位,因而其对航行体的流体动力特性也有着决定性的影响。因此对空化器的研究具有重要的意义。作为空化器的一种,圆盘空化器具有对超空泡形态控制性明显的特点,而且圆盘绕流的流场是轴对称的,只有沿圆盘轴线方向的流体动力,因此有利于航行体的稳定航行。
随着空化理论和计算方法的不断发展,数值方法已经成为研究空化问题的重要手段。目前,研究空化的数值方法主要是求解雷诺平均N-S方程,而由于雷诺应力的出现,导致该方程不再封闭,因此需要补充湍流模型使其封闭。当前应用最多的是标准k-ε湍流模型,然而该模型适合于模拟充分发展的湍流流动,不能用于近壁区的流动模拟,并且模型中的湍流尺度是未知的,使其对湍流的模拟有一定的缺陷[4]。为了更准确模拟湍流,F.R.Menter基于k-ε湍流模型和k-ω湍流模型提出了SST k-ω湍流模型,简称SST湍流模型。该模型保留了k-ω模型的近壁面特性和k-ε模型对来流条件不敏感的优点,并计入了湍流切应力输运的影响,使其可以成功地处理分离流动。此外,还具有能够适应逆压梯度变化的流动现象,无须使用比较容易失真的黏性衰减函数就能精确地模拟边界层现象等优点[5]。
本文利用商业CFD软件Fluent 6.3,采用SST湍流模型对圆盘空化器的空化流动进行仿真,并分析空化数和攻角对其超空泡形态特性和流体动力特性的影响规律,从而为圆盘空化器的进一步研究提供一定的参考依据。
1 数学模型
1.1空化模型
空化流场中包含水、水蒸气和非凝结性气体,它们之间的相互关系由空化模型给出,在Fluent 6.3中采用的空化模型是由A.K.Singhal等人[6]提出的全空化模型。此模型考虑了蒸气泡的形成和运输,压力和速度的不规则波动,液体中非凝结性气体等因素的影响。其相变率表达式为:
当p<Pv时,
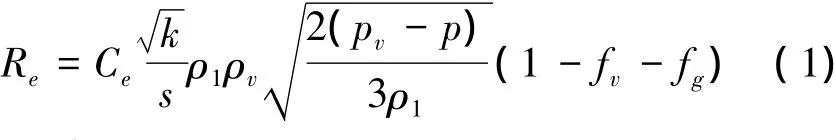
当p>Pv时,
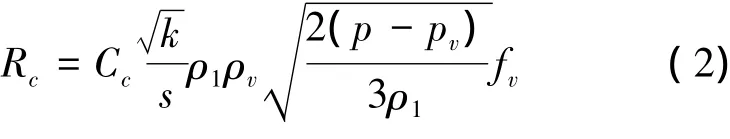
式中: Re和Rc分别为水蒸气的产生率和凝结率,Ce和Cc分别为经验常数,Ce= 0.02,Cc= 0.01,k为局部湍动能,s为水的表面张力系数,ρl和ρv分别为水和水蒸气的密度,p为局部静压,Pv为液体的饱和蒸汽压,fv和fg分别为水蒸气和非凝结性气体的质量分数。
1.2湍流模型
F.R.Menter[7]基于k-ε湍流模型和k-ω湍流模型,并引入Bradshaw假设,提出了SST k-ω两方程湍流模型。模型方程如下:
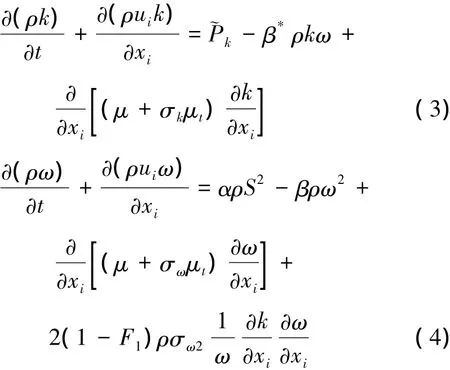
其中,混合函数F1定义如下:

涡黏系数定义为:
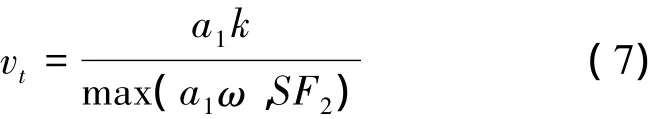
式中,a1= 0.31,混合函数F2定义如下:
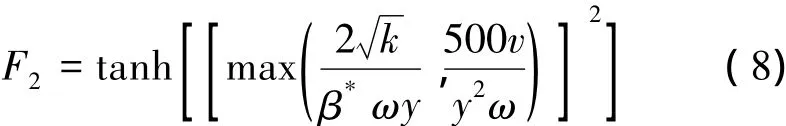
模型中常数的取值为Fluent中的默认值。
2 计算模型
本文采用数值方法对圆盘空化器的空化流动进行模拟,来分析空化数和攻角对其超空泡形态特性和流体动力特性的影响规律,其中圆盘的直径Dn= 100 mm。计算域的前方和外侧设为速度入口,尾部设为压力出口,其中前方边界和外侧边界距离空化器20 Dn,计算域的总长度为100 Dn。划分网格时,在空化流动的核心区域采用了加密的网格,而在远离核心区域的地方适当放宽了网格的尺寸,并且全部采用结构化网格,以保证计算的精度和提高计算的效率。
模拟过程中,圆盘空化器的空化流动是定常的,并采用了混合物模型和隐式的压力基解算器。由于模型中包含了气相和液相,并且两相之间存在质量交换,因此启用了全空化模型。而用来封闭雷诺平均N-S方程的湍流模型采用了SST湍流模型。压力与速度的耦合求解采用SIMPLEC算法,压力梯度项的离散采用PRESTO!格式。
3 仿真结果与分析
在分析空化现象时,空化数是衡量流体空化程度的一个重要的无量纲相似参数,其定义为:
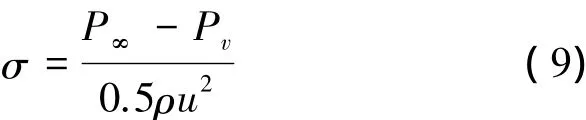
式中,P∞为无穷远处流体静压,Pv为空泡内静压,计算时设为流体的饱和蒸气压,ρ为流体密度,u为来流速度。
3.1仿真模型验证
Rouse和McNown[8]对轴对称回转体进行了一系列的试验,并测量了其表面压力,为以后的研究提供了重要的参考依据。本文利用所建立的数值方法对平头回转体进行仿真,计算了其在空化数为0.3时的空化流动,此时以回转体直径为特征长度的雷诺数为2.56×106。通过处理得到了该回转体表面的压力分布,将其与Rouse和McNown的试验结果进行比较,如图1所示。

图1 平头回转体表面压力分布
由图可知,本文的计算结果与Rouse和McNown的试验结果符合良好,能比较准确地反映出平头回转体发生空化时的表面压力分布,表明了本文数值方法在预测空化方面的有效性。
3.2二维无攻角圆盘空化器仿真
在无攻角运动状态下,圆盘空化器的计算模型是轴对称的,因此将其简化为二维轴对称模型,这样可以极大的缩短模型的计算时间。同时为提高计算精度,在划分网格时,全部采用四边形结构化网格,而不是采用容易影响空泡界面光滑性的非结构化网格。模型共划分了65 110个结构化四边形网格。
本文通过将空化数转化为速度的参数,进而设定来流边界的速度,研究了空化数范围为0.06~0.15时圆盘空化器的空化流动。在该范围内,以圆盘直径为特征长度的雷诺数均大于3.6×106。表1列出了不同空化数下模型的仿真结果,其中包括表征超空泡形态的主要参数,即超空泡最大长度和超空泡最大直径,以及圆盘空化器的阻力系数。
P.R.Garabedian[9]基于势流理论,通过求解轴对称流函数,给出了小空化数下圆盘空化器超空泡最大长度和最大直径的渐进解,其经验公式为:
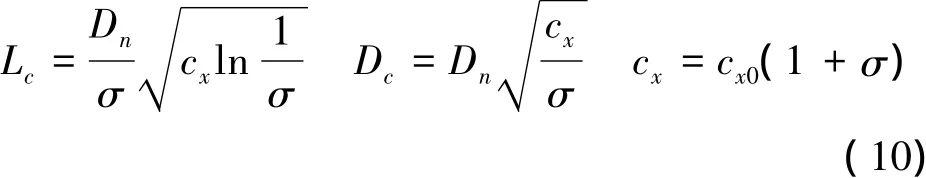
式中,Lc为超空泡最大长度,Dc为超空泡最大直径,cx为圆盘空化器的阻力系数,cx0= 0.827,为圆盘空化器在空化数为零时的阻力系数。
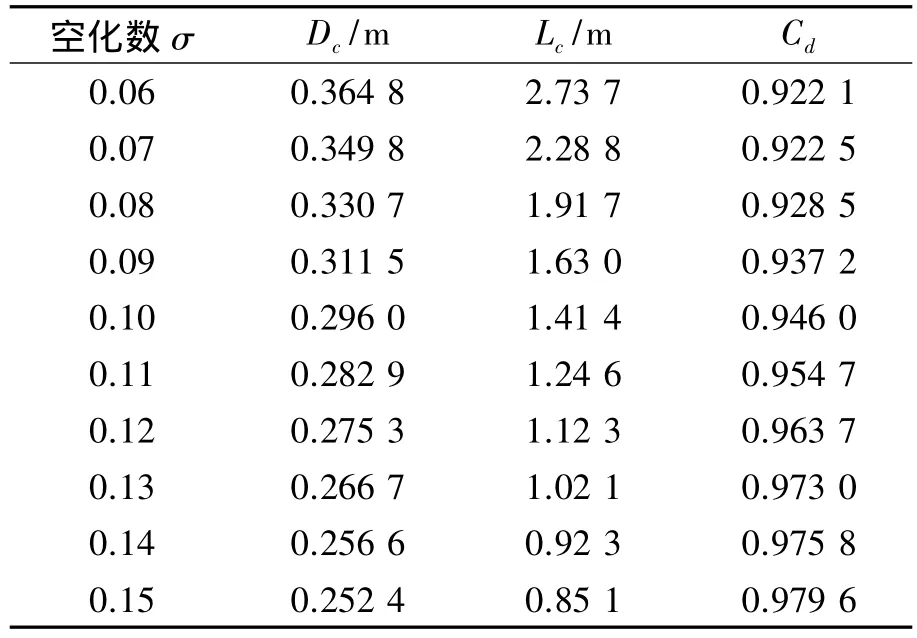
表1 无攻角圆盘空化器仿真结果
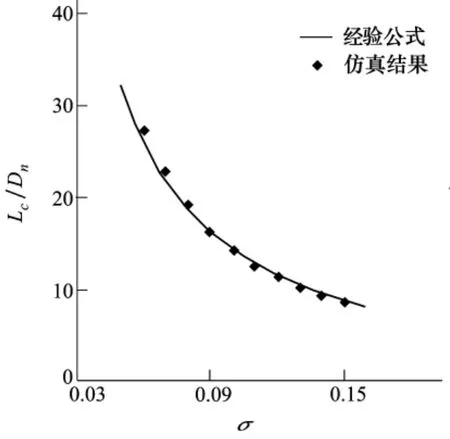
图2 超空泡最大长度随空化数的变化
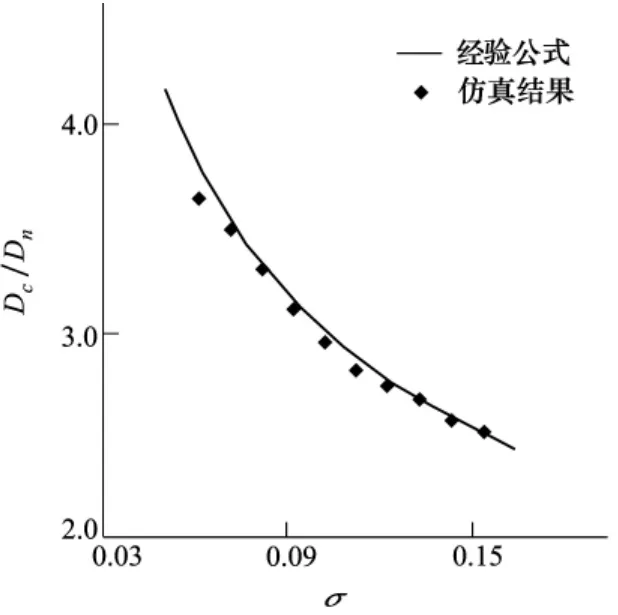
图3 超空泡最大直径随空化数的变化
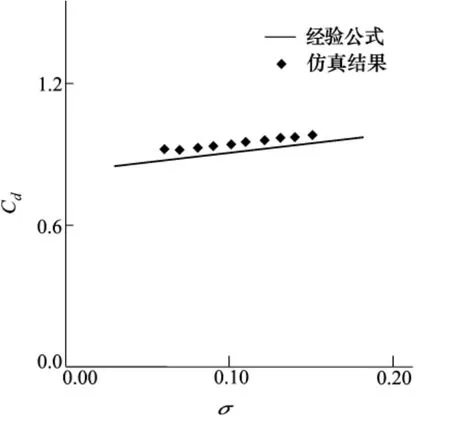
图4 空化器阻力系数随空化数的变化
对超空泡最大长度和最大直径进行无量纲处理,并将所得结果与经验公式进行比较,如图2、图3所示。由图可知,随着空化数的增大,超空泡的最大长度和最大直径逐渐减小,且空化数较小时变化更为明显。图4给出了圆盘空化器的阻力系数随空化数的变化。由图可知,空化器的阻力系数随着空化数的增大而增大,且近似为线性的增加。从图中不难看出仿真计算的结果与经验公式非常接近,即使在空化数较小时二者之间略有不同,但其误差均在精度控制范围内,表明二者具有良好的一致性,从而进一步验证了本文数值方法的可靠性。
3.3三维带攻角圆盘空化器仿真
水下航行体在水中运动时会受到一定的浮力作用,而由于超空泡的出现,其所受的浮力要小于重力。为了维持航行体的平衡,使空化器具有一定的攻角,从而产生一定的升力是有必要的。
空化器的攻角定义为其轴线与来流方向的夹角。本文通过设定来流边界条件来控制空化器的攻角,研究了攻角范围为0°~20°时圆盘空化器的空化流动。其中来流速度的大小均为50 m/s,所对应的空化数为0.079 3。在研究中,空化器和流场不再具有轴对称特性,因此需要建立全流场的三维计算模型,并利用三维求解器进行求解。然而计算模型相对于空化器的运动平面是对称的,因此只建立一半的三维计算模型。计算网格全部采用六面体结构化网格,网格数为1 057 810。
图5给出了不同攻角下圆盘空化器生成超空泡的水蒸气体积分数云图。从图中可以看出,无攻角圆盘空化器所生成的超空泡是对称的,并且产生了十分明显的回射流。当空化器以不为零的攻角运动时,生成的超空泡不再具有对称性,且随着攻角的增大,超空泡的不对称性越来越明显,而回射流现象则越来越不明显,直至消失。
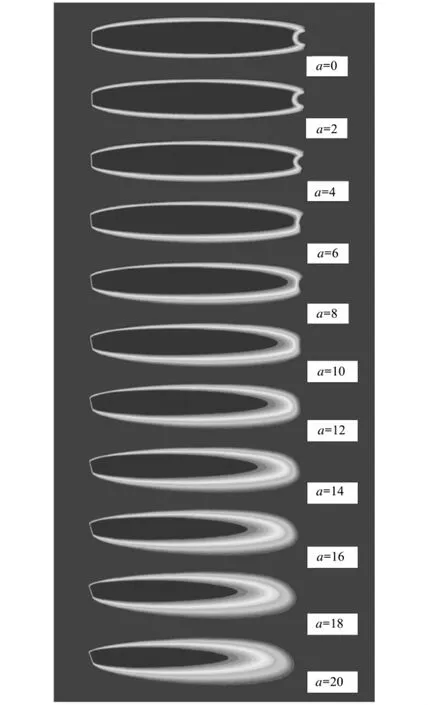
图5 不同攻角下圆盘空化器生成超空泡的水蒸气体积分数云图
图6、图7、图8分别给出了不同攻角下超空泡的最大长度、最大直径和长细比(K=Lc/Dc)。从图中可以看出,超空泡的最大长度和最大直径均随着攻角的增大而逐渐减小,超空泡的长细比先是随着攻角的增大有小幅度增大,而后随着攻角的增大亦逐渐减小。
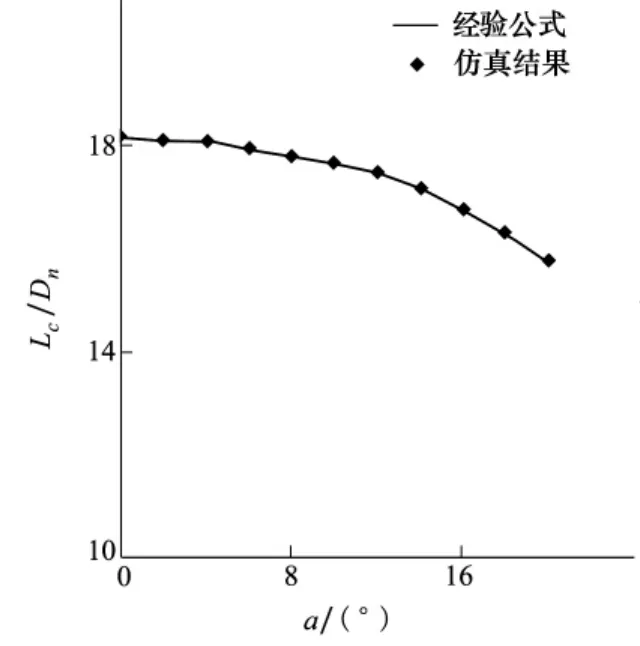
图6 超空泡最大长度随攻角的变化
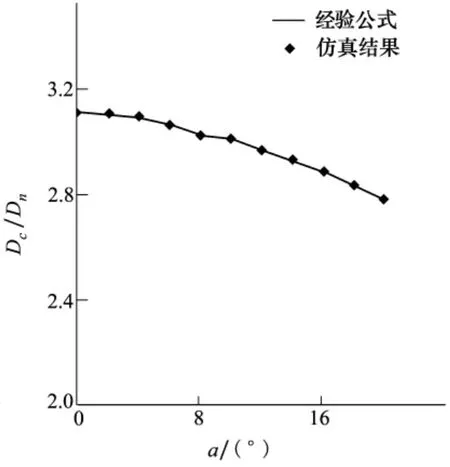
图7 超空泡最大直径随攻角的变化
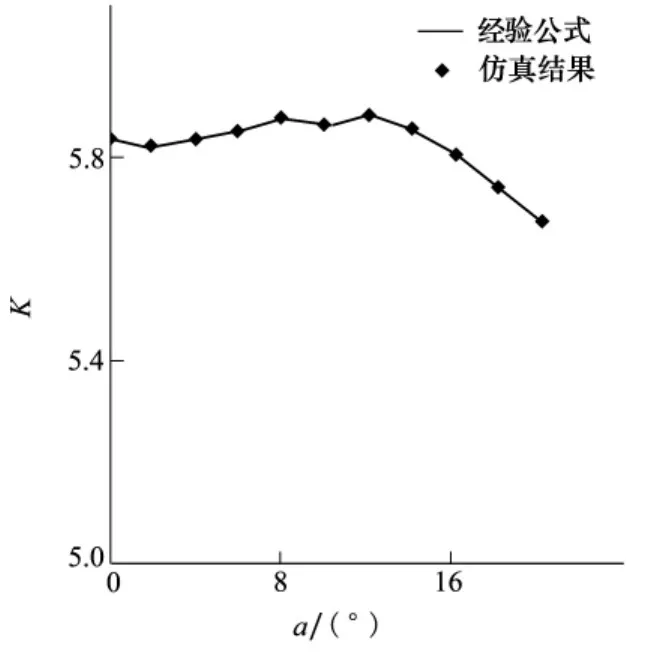
图8 超空泡长细比随攻角的变化
图9、图10、图11分别给出了不同攻角下圆盘空化器的阻力系数、升力系数和升阻比(Ck= Cl/ Cd)。从图中可以看出,攻角对圆盘空化器的流体动力特性有比较大的影响,尤其是对升力系数有着直接的影响。在研究的攻角范围内,空化器的阻力系数随着攻角的增大而逐渐减小,且减小幅度有增大的趋势,这对超空泡的减阻是非常有利的;其升力系数随着攻角的增大而近似线性的增大,因此在应用中可以根据实际需要调节空化器的攻角,以获得适当的升力;其升阻比随着攻角的增大而逐渐增大。
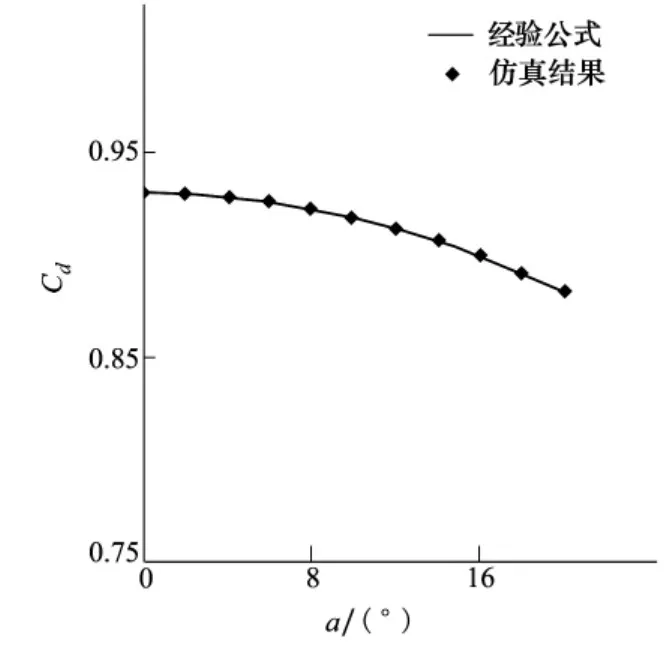
图9 空化器阻力系数随攻角的变化
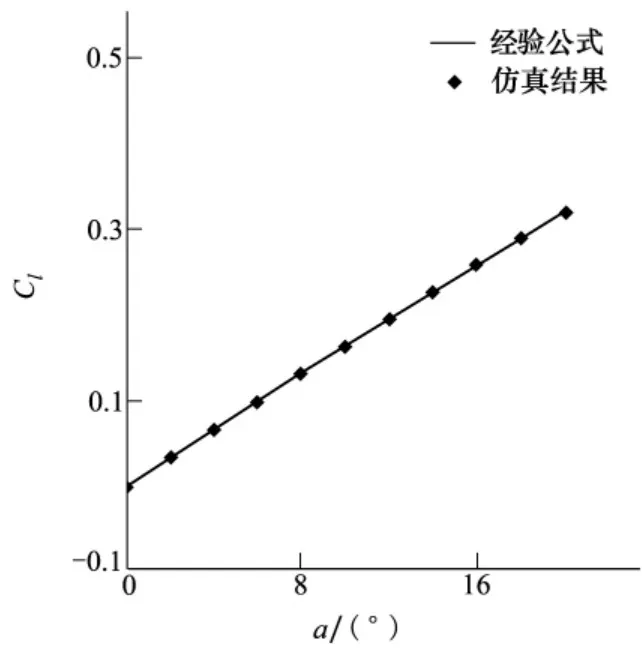
图10 空化器升力系数随攻角的变化
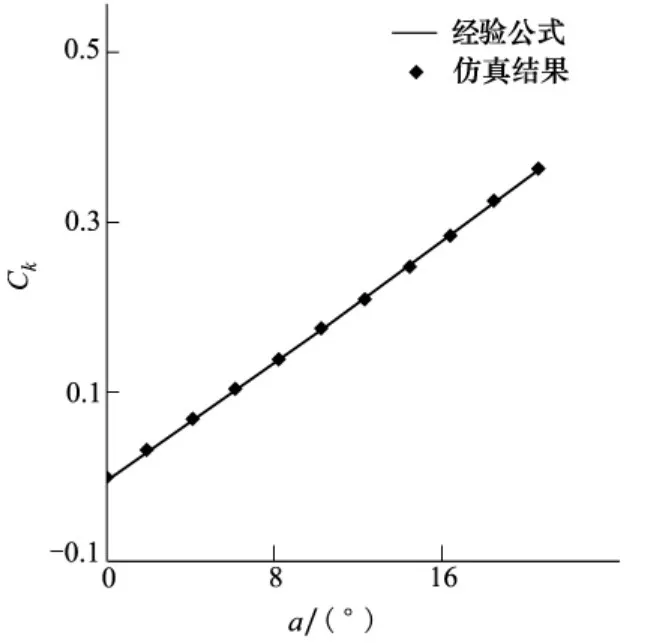
图11 空化器升阻比随攻角的变化
4 结论
1)对平头回转体进行仿真,并分析其表面的压力分布,所得结果与Rouse和McNown的试验结果符合良好,表明了本文数值方法在预测空化方面的有效性。
2)无攻角圆盘空化器在水下运动时,生成超空泡的最大长度和最大直径均随着空化数的增大而减小,其阻力系数随着空化数的增大而增大。将仿真结果与经验公式进行比较,二者具有良好的一致性,进一步验证了本文数值方法的可靠性。
3)空化器的攻角会对超空泡的尺寸和形状产生影响。超空泡的最大长度和最大直径均随着攻角的增大而减小,其长细比随着攻角的增大则先增大后减小。在攻角的作用下,超空泡不再是对称的,其不对称性随着攻角的增大越来越明显,而尾部回射流现象随着攻角的增大越来越不明显,直至消失。
4)空化器的攻角对其流体动力特性有比较大的影响,尤其是对升力系数有着直接的影响。在研究的攻角范围内,其阻力系数随着攻角的增大而减小,其升力系数和升阻比随着攻角的增大而增大。
参考文献:
[1]颜开,褚学森,许晟,等.超空泡流体动力学研究进展[J].船舶力学,2006,10(4) : 148-155 Yan Kai,Chu Xuesen,Xu Sheng,et al.Research Progress of Supercavitation Hydrodynamics[J].Journal of Ship Mechanics,2006,10(4) : 148-155 (in Chinese)
[2]曹伟,魏英杰,王聪,等.超空泡技术现状、问题与应用[J].力学进展,2006,36(4) : 571-579 Cao Wei,Wei Yingjie,Wang Cong,et al.Current Status,Problems and Applications of Supercavitation Technology[J].Advances in Mechanics,2006,36(4) : 571-579 (in Chinese)
[3]杨莉,张庆明.超空泡技术的应用现状和发展趋势[J].战术导弹技术,2006(5) : 6-10 Yang Li,Zhang Qingming.Current Application and Perspectives on Supercavitation Technology Research[J].Tactical Missile Technology,2006(5) : 6-10 (in Chinese)
[4]Shih T H,Liou W W,Shabbir A,et al.A New k-ε Eddy Viscosity Model for High Reynolds Number Turbulent Flows[J].Computers Fluids,1995,24(3) : 227-238
[5]Menter F R,Kuntz M,Langtry R.Ten Years of Industrial Experience with the SST Turbulence Model[J].Turbulence,Heat and Mass Transfer,2003(4) : 625-632
[6]Singhal A K,Athavale M M,Li H,et al.Mathematical Basis and Validation of the Full Cavitation Model[J].Journal of Fluids Engineering,2002,124(3) : 617-624
[7]Menter F R.Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications[J].AIAA Journal,1994,32(8) : 1598-1605
[8]Rouse H,Mcnown J S.Cavitation and Pressure Distribution,Head Forms at Zero Angle of Yaw[R].Iowa City: State University of Iowa,1948
[9]Garabedian P R.Calculation of Axially Symmetric Cavities and Jets[J].Pacific Journal of Mathematics,1956,6(4) : 611-684
Numerical Simulation on Supercavity Characteristics of Disc Cavitator Based on SST Turbulence Model
Hou Baoxin,Zhi Xizhi,Liu Yongshou,Liu Wei
(Department of Engineering Mechanics,Northwestern Polytechnical University,Xi'an 710129,China)
Abstract:Based on the full cavitation model and SST k-ω turbulence model,the cavitating flow of disc cavitator is simulated with commercial CFD code Fluent 6.3.First,results are presented for the pressure distribution on the surface of an axisymmetric blunt body and they show good agreement with the experimental data of Rouse and Mc-Nown,which,we believe,validates the effectiveness of the proposed numerical method.Next,the characteristics of supercavity shape and drag of disc cavitator for zero attack angle are obtained for different cavitation numbers; these are used to analyze the impact of cavitation number on cavitating flow.The results are compared with the empirical formula and they show good consistency.Lastly,the cavitating flow of disc cavitator with variable attack angle is simulated and the impact of attack angle on the characteristics of supercavity shape and hydrodynamic is analyzed.Studies show preliminarily that: (1) both cavitation number and attack angle have an effect on the main dimensions of supercavity and the attack angle also has a significant effect on the symmetry and reentrant jet phenomenon; (2) the attack angle has a relatively large effect on the hydrodynamic characteristics of disc cavitator and especially it has a direct effect on the lift coefficient.These results,we believe,are valuable in the application of disc cavitator to submerged moving bodies.
Key words:angle of attack,cavitation,computational efficiency,computational fluid dynamic,computer simulation,computer software,drag,drag coefficient,efficiency,experiments,hydrodynamics,lift,lift drag ratio,mathematical models,mesh generation,pressure distribution,turbulence models; cavitation number,SST turbulence model,supercavity shape
作者简介:侯保新(1989—),西北工业大学硕士研究生,主要从事水下航行体空化特性研究。
收稿日期:2014-09-12基金项目:高等学校学科创新引智计划项目(B07050)与陕西省自然科学基础研究计划(2013JM6011)资助
文章编号:1000-2758(2015) 02-0259-06
文献标志码:A
中图分类号:TJ63

