基于变增益互补滤波的FADS/INS融合方法*

肖地波, 蒋保睿, 张 勇, 王志强, 林 茜

(1.成都信息工程大学 自动化学院，四川 成都 610225；2.南京航空航天大学 无人机研究院，江苏 南京 211106；3.湖南华南光电集团有限责任公司，湖南 常德 415005)

0 引 言

嵌入式大气数据传感(flush air data sensing,FADS)系统无突出飞行器表面外的部件，能够用于高超声速、隐身等现代先进飞行器，同时，整个系统无机械活动部件，降低了维护时间和成本[1]，被认为最有前景的攻角和侧滑角等大气数据测量系统之一。近年来，FADS相关研究主要集中在气动模型和解算[2,3]、校准[4]、FADS系统设计和测试[5]、故障检测和容错[6]、误差分析[7]等。目前,主要的研究集中于对解算过程进行改进[8]、与其他信号源信息融合[9～15]等方面。

由于FADS在机动飞行时存在压力测量延迟，而惯性导航系统(inertial navigation system,INS)能够快速响应飞行器姿态变化，与FADS形成良好的互补，因此经常将二者融合解算。按照信息融合的层次，FADS/INS融合方法可以分为两类：一类是决策层的融合，如在X—34再入过程中，采用互补滤波器来融合FADS侧滑角和INS侧滑角，以降低高速再入过程中侧风影响[10]，采用偏差滤波器来融合FADS攻角和INS攻角[11]，这类算法简单容易实现，但由于机动飞行和巡航时对滤波器参数需求相互矛盾，导致难以在整个飞行阶段维持高精度；另一类是数据层的融合，这类方法主要是建立观测模型，采用卡尔曼滤波方法来估计一些大气数据信息，如肖地波等人融合FADS和INS来估计大气风，再结合INS数据获得攻角和侧滑角[12,13]；Karlgaard C D等人融合FADS、INS和先验的大气模型信息来实时估计大气数据[14]；Hove等人融合FADS和INS在飞行后重构大气数据[15]。这类方法采用高阶滤波模型时精度高，但计算复杂度也高，低阶模型则精度迅速下降。

本文在这些研究的基础上，提出一种改进的变增益互补滤波方法来融合FADS攻角/侧滑角和INS攻角/侧滑角，采用低阶滤波器实现整个飞行阶段的攻角/侧滑角高精度估计，兼顾了计算复杂度和攻角/侧滑角估计精度。

1 基于互补滤波的FADS/INS融合特点

1.1 INS攻角和侧滑角测量原理及特点

在不考虑风速的情况下，利用INS的速度信息，可以计算惯性攻角αINS和侧滑角βINS

(1)

式中UB，VB，WB为惯性速度在机体坐标系X，Y，Z三轴上的分量。

惯性攻角是惯性速度的函数，无风时，惯性攻角的误差主要惯性测量器件引起，惯性测量器件(如陀螺仪)的误差可以通过一阶马尔可夫过程来建模

Vk=βINSVk-1+δINS,k

(2)

式中V为INS速度，βINS和δINS分别为马尔可夫过程相关系数和白噪声标准差。

INS系统能够迅速响应飞行器自身姿态变化(如爬升、下降等)引起的攻角/侧滑角变化。但如果存在阵风或大气紊流，INS不能及时响应阵风和紊流等气流改变导致的攻角/侧滑角变化。因此，在机动飞行时，自身状态变化的影响站攻角/侧滑角变化的主要部分，INS能够及时响应这种变化，误差相对较小；而稳态飞行时，飞行器攻角/侧滑角的改变主要是由于气流状态变化造成的，INS不能及时响应，因而误差较大。

1.2 FADS攻角和侧滑角测量原理及特点

FADS在飞行器表面(通常在飞行器头部)布置一系列测压孔，通过引气管路将压力引入飞行器内部的压力传感器，由压力传感器测得各测压孔处压力，再反过来求解攻角和侧滑角。本文研究的FADS系统测压孔布局如图1所示。

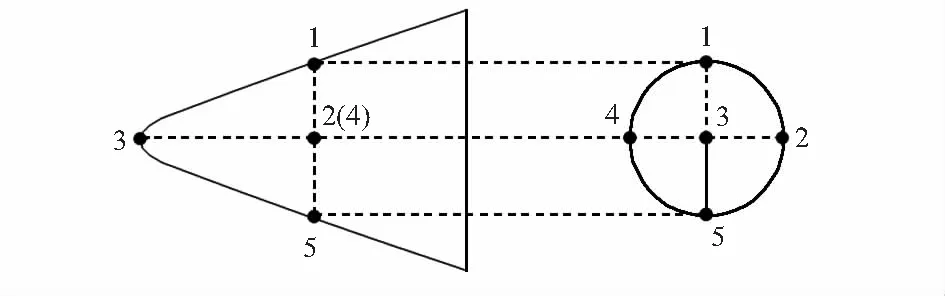
图1 FADS测压孔布局

对于图 1所示的FADS布局，可以采用三点法来求解攻角和侧滑角[2]

(3)

上式中符号A,B,A′,B′,C′的具体表达式见参考文献[2]，此处不再赘述。

测压孔通过引气管路与压力传感器相连，压力传播时造成的误差是FADS的主要误差之一，压力在引气管路中间的传播过程可以建模为1个二阶系统[12]

(4)

式中P0,i为第i个测压孔处飞行器表面压力，PL,i为对应测压孔压力传感器处的压力，ωn为自然频率，ζ为阻尼比，其具体表达式见参考文献[12]。

压力测量误差是FADS系统的另一个重要误差，飞行器表面压力与自由流的偏差，产生的机理较为复杂，测量噪声的产生机理也比较复杂[16]，考虑到误差中包含稳态分量和白噪声分量，此处将该误差和压力测量误差合并通过一阶马尔科夫过程来建模

P=PT+ΔP，Δ=rΔP+ωP

(5)

式中P为FADS测得的压力值，PT为真实压力，ΔP为马尔科夫过程误差，r为马尔科夫相关系数，ωP为压力测量白噪声。

1.3 FADS/INS互补滤波原理

从以上分析过程可以看出，INS在机动飞行时能够及时响应攻角/侧滑角的变化，稳态飞行时则存在较大误差；FADS在稳态飞行时误差较小，而在机动飞行时由于压力传播延迟导致存在较大的误差，二者正好互补，可以通过互补滤波来融合FADS攻角/侧滑角和INS攻角/侧滑角。FADS攻角通过一个低通滤波器，以利用其精确的稳态分量；INS攻角通过一个高通滤波器，以利用其及时响应的攻角/侧滑角动态变化，再进行叠加，输出攻角为

(6)

互补滤波器滤波常数τ对输出有明显影响，τ越大，FADS迎角分量越少的计入了融合后的输出结果，惯性迎角分量越多的计入了融合后的输出结果。因此，当飞行器机动飞行时，τ可选得大一些，平飞时，τ可选得小一些。

2 变增益互补滤波算法设计

2.1 固定增益互补滤波方法分析

根据式(6)所示的互补滤波融合原理公式，将其离散化，可得滤波方程

(7)

式中 Δt为离散时间，在实际飞行器中，是系统采样时间，确定后为常值，常规的互补滤波采用固定的滤波常数τ，当τ分别取0.1,1,10时攻角输出如图 2(a)所示，图(b)为图(a)在65～70 s间曲线的局部放大。

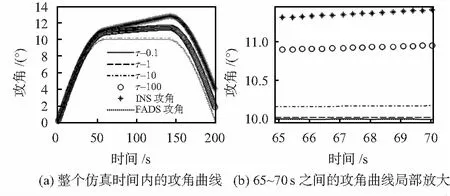
图2 不同τ时互补滤波输出攻角

从图 2可见，τ越大，越接近INS攻角；τ越小，越接近FADS攻角。FADS在机动飞行段的误差大，INS在稳态时误差大。因此，机动飞行时和巡航飞行时对滤波器参数的需求是不同的，为了保持整个飞行阶段的攻角输出精度，往往在两者之间进行折中。

2.2 变增益互补滤波算法

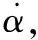
(8)

(9)

将式(8)和式(9)代入式(7)，可得攻角融合公式

(10)

这样，可知变增益互补滤波算法结构如图3所示。

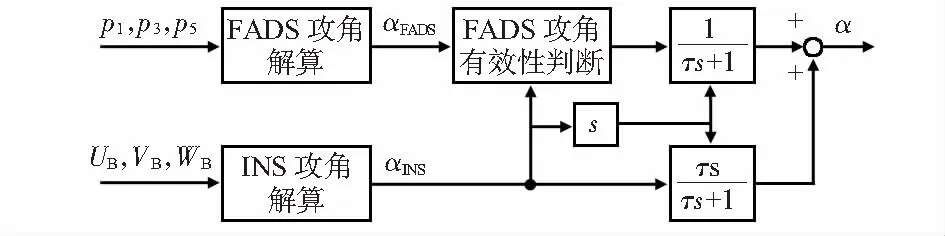
图3 攻角变增益互补滤波算法结构

具体计算过程为：1)根据第1,3,5号测压孔的压力数据，采用式(3)所示的三点法公式计算出FADS攻角;2)根据式(1)从INS系统测得的三轴速度UB、VB、WB和姿态中计算出惯性攻角;3)判断FADS攻角是否有效：考虑到FADS延迟如果过大可能导致其失去意义，根据INS攻角来判断FADS攻角是否仍然有效，如果式(11)成立则FADS攻角有效,式(11)表明，如果FADS攻角与上一时刻的攻角加上INS攻角变化量的偏差超过阈值ε，则认为FADS攻角失效;4)如果FADS攻角失效，以上一时刻的FADS攻角加上INS攻角变化量作为当前FADS攻角与INS攻角融合;5)根据式(9)计算惯性攻角的变化率，如果k=1，则用初始将滤波常数设为初值;6)根据式(8)计算出当前时刻滤波器的滤波常数;7)计算通过低通滤波器后的FADS攻角和高通滤波器后的INS攻角，并将二者叠加，输出融合后的攻角。式(11)如下

|αFADS,k-1+αINS,k-αINS,k-1-αFADS,k|≤ε

(11)

侧滑角的融合方法与攻角的类似，只是计算FADS侧滑角时根据第2,3,4号测压孔压力计算，其余完全相同，此处不再重复。

3 仿真与分析

假设飞行轨迹包括上升、平飞和下降过程，FADS压力测量误差采用式(5)所示的一阶马尔可夫过程来建模，压力传递延迟采用式(4)所示的二阶系统来描述；INS测量误差采用式(2)所示的一阶马尔可夫过程加惯性器件漂移误差来描述。FADS攻角、INS攻角、变增益互补滤波融合攻角如图4(a)所示，图(b)是图(a)在60～140 s间曲线的局部放大。

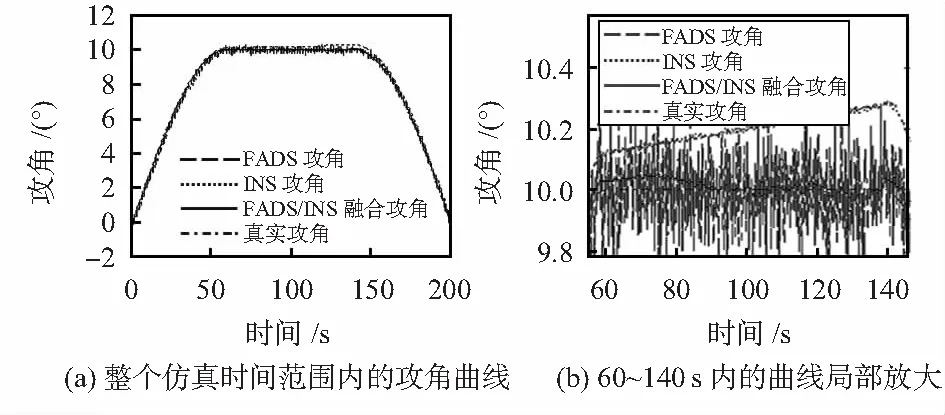
图4 变增益互补滤波融合攻角曲线

从图4中可以看出，变增益互补滤波融合方法得到的攻角能够反映整个飞行阶段内攻角的变化规律，误差较小。变增益互补滤波融合攻角误差曲线与FADS攻角误差曲线和INS攻角误差曲线，如图5(a)所示，变增益互补滤波器的滤波常数变化曲线如图5(b)所示。

从图5(a)中可以看出，在整个飞行阶段内，变增益互补滤波算法输出的攻角误差/侧滑角误差都小于FADS攻角/侧滑角误差，也小于INS攻角/侧滑角误差，说明了变增益互补滤波算法是有效的，能够同时保证巡航和机动阶段的攻角/侧滑角输出精度。从图5(b)中可以看出，在飞行开始阶段(上升过程中，攻角变化快)和结束阶段(下降阶段，攻角变化快)，滤波时间常数很大，并随着攻角变化而变化；而在巡航飞行阶段(攻角几乎不变)，滤波时间常数很小。说明了变增益互补滤波算法能够有效的根据飞行状态改变滤波器时间常数，达到改善输出精度的目的。

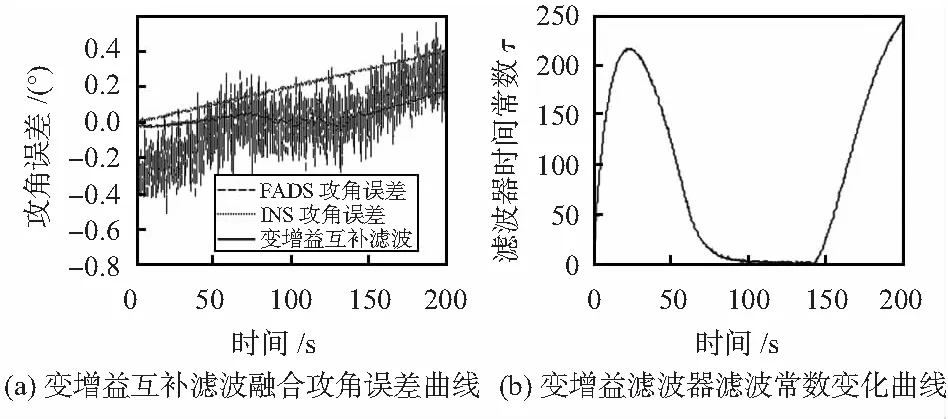
图5 变增益互补滤波融合攻角误差和滤波常数变化曲线

整个飞行轨迹上变增益互补滤波与常规固定增益互补滤波方法(滤波常数τ分别取1,50和500)得到的攻角/侧滑角误差曲线对比如图6所示，图(b)为图(a)在36～41 s间曲线的局部放大。从图6中可以看出，不论固定增益互补滤波的滤波常数取何值，变增益互补滤波的整体精度更好，误差不超过0.2°。对于侧滑角的仿真方法与攻角相同，得到的结论也类似，此处不再赘述。

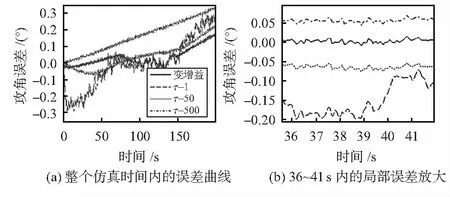
图6 变增益互补滤波与常规固定增益互补滤波得到的误差曲线比较

4 结 论

通过本文的研究可以得到以下结论：

1)变增益互补滤波方法能够利用FADS攻角/侧滑角中的低频成分和INS攻角/侧滑角中的高频成分来提高攻角/侧滑角测量精度；

2)在整个飞行阶段，变增益互补滤波能够根据当前的飞行状态自动调整滤波常数，以适应飞行状态变化；

3)基于变增益互补滤波的FADS/INS融合方法较传统的固定增益互补滤波，能够更好地保持整个飞行轨迹上的攻角/侧滑角测量精度。