基于二自由度模型驱动PID的CFB锅炉床温控制
吴丹丹 ,张丽香,贾建东,张培华 ,樊泽明
(1.山西大学 自动化系,太原 030013;2.中北大学 机械与动力工程学院,太原 030051;3.山西平朔煤矸石发电有限责任公司,朔州 036800;4.中电神头发电有限责任公司,朔州 036013)
循环流化床锅炉具有污染物排放少、燃料适应性广、燃烧效率高、易于实现灰渣综合利用等优点,在工业和商业领域得到广泛应用[1],特别是随着国内煤炭资源情况变化,国内越来越重视利用CFB技术燃用低热值燃料[2]。但是,由于循环流化床锅炉是一个分布参数时变、非线性、多变量紧密耦合的控制对象,且主汽压和床温之间存在强耦合关系,这给床温自动控制带来较大困难。循环流化床锅炉床温的稳定与否直接影响锅炉运行中的脱硫效率及氮氧化物的生成量。床温过低,不但使锅炉效率下降,而且使锅炉运行不稳定,容易灭火;床温过高,会使炉内脱硫效率下降,氮氧化物的产生量大大增加,同时容易造成炉膛内料床结渣,导致锅炉出力下降,甚至被迫停炉。因此,锅炉运行床温应控制在830℃~870℃之间为最佳[3]。综合以上因素可知,固定参数的常规控制器已经很难满足复杂多变的CFB锅炉燃烧控制系统的控制性能。因此,控制专家们一直在寻求新的控制策略。
模型驱动控制(MDC)的概念由Kimura在2000年的悉尼控制与决策国际会议上提出,并将模型驱动控制定义为采用过程模型作为控制器的主要组成部分,对被控过程实现自动控制。Masanori[4]等在2002年提出的二自由度模型驱动PID控制已经能够初步应用在大迟延、大惯性的系统中。基于模型驱动PID控制策略的应用研究还处在起步阶段:TDFMD PID被应用在CFB锅炉主蒸汽压力控制的仿真研究中,结果表明:此控制方法明显优于常规PID控制[5-6]。本文将TDFMD PID控制方法应用在复杂多变的CFB锅炉床温控制中,使控制性能大幅度提高。
1 CFB锅炉床温的动态特性
CFB锅炉床温受多种因素的影响,包括给煤量、煤质、一次风量、二次风量和循环灰量等等,其中影响较大的因素有给煤量、一次风量和循环灰量[1]。床温与主蒸汽压力是一对强耦合的变量,二者都是通过调节给煤量、一次风量来达到控制目的。考虑送风系统的频繁动作不利于整个系统的稳定,文献
[7]提出的“空气-床温”系统实现了蒸汽压力与床温的完全解耦。因此,本文主要考虑通过调节给煤量来控制床温。
在给煤量阶跃扰动下,现场辨识得到的床温被控对象的动态特性可近似用如下传递函数来描述[1]:
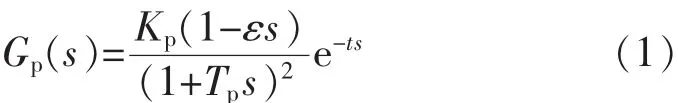
式中:Kp为静态增益;Tp为时间常数;t为延迟时间。ε值一般保持在12左右,基本保持不变,其他参数都随锅炉运行工况的不同而改变。当锅炉负荷在25%~100%范围内变化时,过程参数的变化范围Kp为 5~10;Tp为 100~200;t为 30 s~60 s。
图1为3种不同负荷下,控制对象的开环动态特性响应曲线,分析得知,当负荷变大时,控制对象的延迟时间和调节时间相应变大,控制难度也加大。大纯滞后的存在使开环系统相位滞后增大,幅值裕度和相位裕度减小,结果使得系统的稳定性降低、动态品质下降[8]。
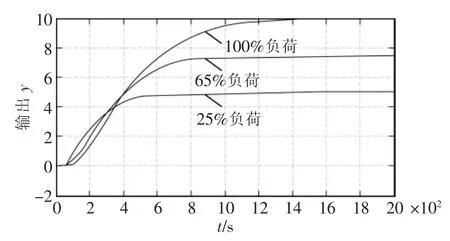
图1 开环动态特性响应曲线Fig.1 Response curve of the open loop dynamic characteristic
2 二自由度模型驱动PID控制系统
二自由度模型驱动PID控制系统的结构框图如图2所示,该系统由3大部分组成:设定值滤波器 Gf(s)、主控制器 Gm(s)和等效被控对象 G0(s)。 图中:r为设定值;e为系统偏差;v为主控制器输出;u为控制变量;d为干扰信号;y为被控量。下面分别介绍各组成部分的工作原理。
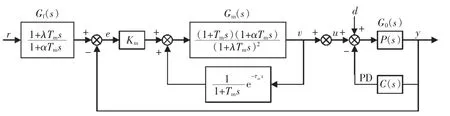
图2 TDFMD PID控制系统结构Fig.2 Block diagram of the TDFMD PID control system
2.1 等效被控对象G0(s)
如图2所示,等效被控对象G0(s)是由实际被控过程P(s)经过 PD反馈补偿环节C(s)补偿后的特性。经补偿后的被控过程变成带有迟延的一阶对象。等效被控对象(以v为输入,y为输出)的传递函数如式(2)所示。其中,K、T、τ分别为等效被控对象的静态增益、惯性时间常数和延迟时间。
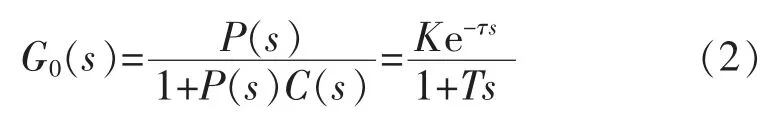
PD补偿器的传递函数为
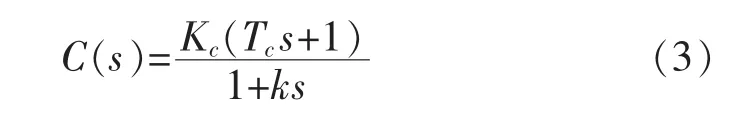
等效被控对象的增益K、惯性时间常数T和迟延 τ参数的取值取决于 C(s)的参数,即 K=Kc,T=Tc,k的取值一般在0.05~0.2之间。反馈补偿器的设计和等效被控对象的确定详见参考文献[5]。
2.2 主控制器Gm(s)
主控制器由增益Km、带有可调参数的二阶滤波器和带有时滞的一阶模型3个模块组成。这个带有时滞的一阶惯性环节的参数来自于等效被控对象G0(s)相对应的参数,即 Tm=T,τm=τ。 取 Km=1/K,则主控制器传递函数的推导过程为

通过调整式(4)中λ和α的值最大程度提高主控制器Gm(s)的控制性能。λ和α一般在0~1之间取值,当λ增大,响应速度变慢;λ减小,响应速度变快,同时也可能产生超调,降低鲁棒性。α对闭环系统的响应速度和稳定性的影响正好相反。
图2所示系统的开环传递函数(从偏差e到输出 y)为
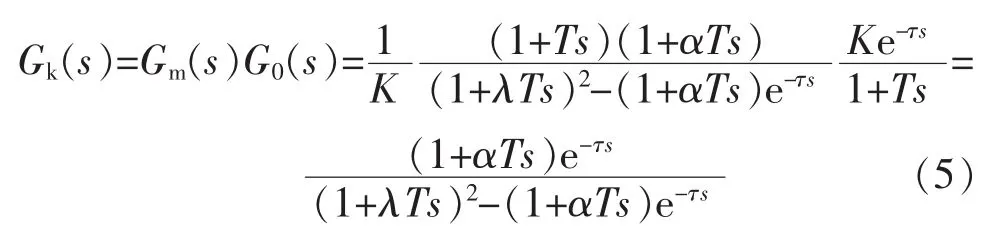
2.3 设定值滤波器Gf(s)
由于Tm=T,所以设定值滤波器的传递函数为
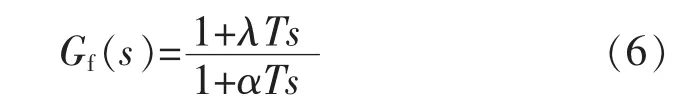
由式(5)和式(6)可得该控制系统的闭环传递函数为
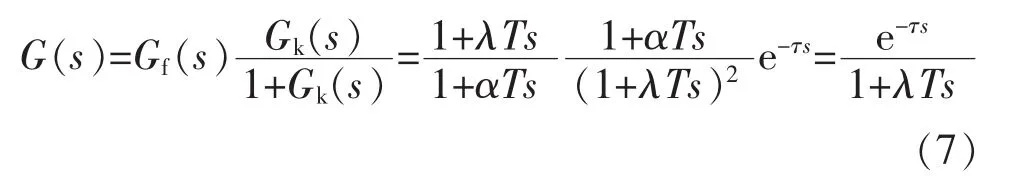
可见,设定值滤波器消去了系统中的一个零点和一个极点,使二阶系统变成了一阶系统,该一阶系统的稳态误差为零。显然,主控制器提高了控制系统的响应速度和抗干扰性能。
3 基于TDFMD PID的CFB锅炉床温控制系统仿真研究
以循环流化床锅炉床温为被控对象,采用Matlab软件对常规PID控制系统和TDFMD PID控制系统分别进行仿真试验。基于上文给出的给煤量扰动下床温被控对象的传递函数和各参数的变化范围,利用线性近似法,得到3种典型工况(25%负荷、65%负荷、100%负荷)下的传递函数如表1所示。

表1 3种典型工况下床温的近似传递函数Tab.1 Approximate transfer function of three kinds of typical operating conditions of the bed temperature
根据表1中的床温对给煤量的近似传递函数,得出常规PID控制系统的响应曲线如图3所示。
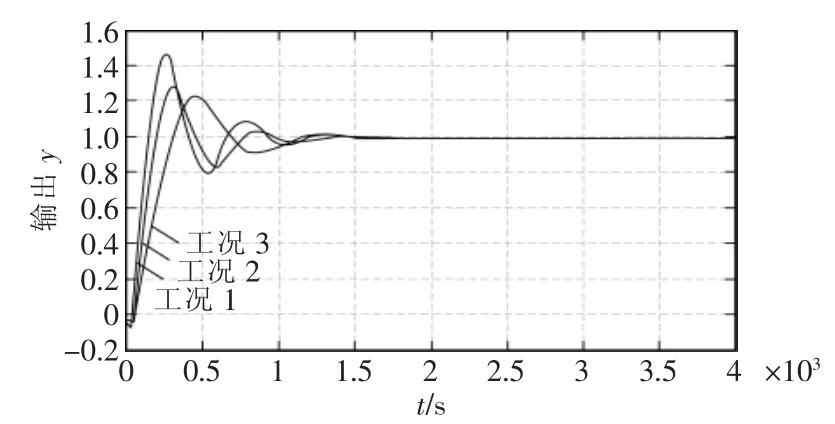
图3 常规PID控制系统的响应曲线Fig.3 Response curves of conventional PID control system
根据TDFMD PID控制系统的工作原理[9],求得3种工况下的过程传递函数的反馈补偿器C(s)及经补偿后的等效被控对象G0(s)如表2所示。

表 2 3 种工况下的 C(s)及 G0(s)值Tab.2 Values of C(s) and G0(s)in three kinds of working conditions
由TDFMD PID控制系统的设计、计算过程和参数整定方法[5]得到3种典型工况下各参数的值如表3所示。TDFMD PID控制系统的响应曲线如图4所示。
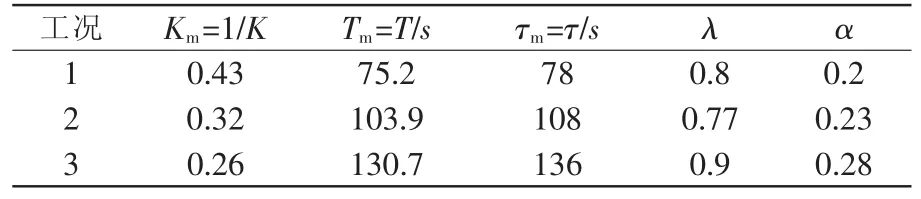
表3 TDFMD PID控制系统的参数设置Tab.3 Parameter setting of TDFMD PID control system
图3和图4比较可见,基于TDFMD PID的循环流化床锅炉床温控制系统,调节时间为1000 s左右,且几乎没有超调。而常规PID控制系统的调节时间在2000s左右,工况1下的超调量最大,可达45%。
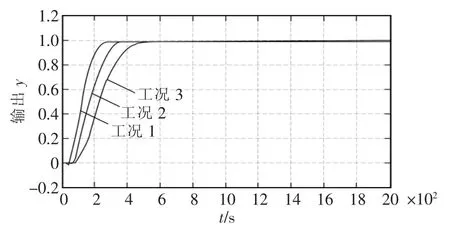
图4 TDFMD PID控制系统的响应曲线Fig.4 Response curve of TDFMD PID control system
当被控过程参数值变化5%(其他参数值都不变)时,3种工况下的过程参数值分别变为工况1,Kp1=5.25,Tp1=105,t1=31.5 s;工况 2,Kp2=7.875,Tp2=157.5,t2=47.25 s;工况 3,Kp3=10.5,Tp3=210,t3=63 s。
图5和图6分别是当过程参数变化5%时,常规PID控制系统和TDFMD PID控制系统的响应曲线。
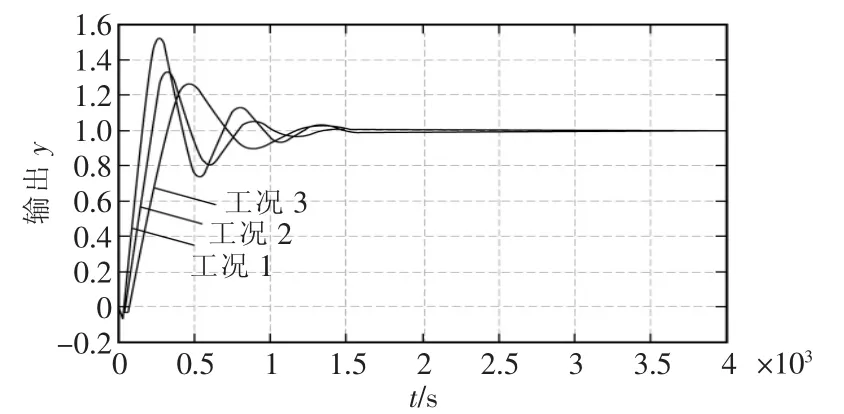
图5 过程参数变化5%时常规PID控制系统响应曲线Fig.5 Response curve of the conventional PID control system with the change of process parameters 5%
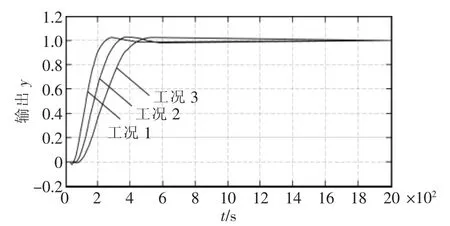
图6 过程参数变化5%时TDFMD PID控制系统响应曲线Fig.6 Response curve of TDFMD PID control system with the change of process parameters 5%
由图5和图6可知,当过程参数变化5%时,基于TDFMD PID的CFB锅炉床温控制系统的调节时间在700 s左右,出现很小的超调量;常规PID控制系统的调节时间由原来的1500 s变为2000 s,超调量也变大。显然,TDFMD PID控制系统较常规PID控制系统有很好的抗干扰能力、鲁棒性和实时跟踪能力,能满足当运行工况发生变化时,CFB锅炉床温的变化在设定值允许范围内波动的要求。
4 结语
由以上仿真可知,TDFMD PID控制系统的调节时间短,超调量小,当过程参数发生变化时,调节时间和超调量的变化幅度很小,具有很强的抗干扰能力和实时跟踪能力。该控制系统结构简单,参数易于调整,鲁棒性好,明显优于常规PID控制,能更好地满足CFB锅炉床温的控制要求。
[1]牛培峰.大型国产循环流化床锅炉燃烧过程智能控制系统应用研究[J].中国电机学报,2000,20(12):62-71.
[2]巩李明,胡国中,苏虎,等.CFB锅炉利用低热值燃料的选择[J].东方电气评论,2014,28(2):24-30.
[3]张栾英,李建强,谷俊杰,等.100 MW循环流化床锅炉床温控制策略[J].华北电力大学学报,2004,31(1):44-47.
[4]Masanori Y,Takashi S,Yasushi B.A two degrees of freedom PID control system,its features and applications[C]//2004 5th Asian Control Conference.Melbourne,Australia:Institute of Electrical and Electronics Engineers Inc,2004:456-459.
[5]张丽香,王晓伟,降爱琴.二自由度模型驱动PID控制系统参数整定方法及应用[J].南京理工大学学报,2014,48(4):476-480.
[6]沈霞,张丽香,王晓伟.基于TDOF MD PID的循环流化床锅炉主蒸汽压力控制系统研究[J].热力发电技术,2014,43(5):94-97.
[7]焦健.循环流化床燃烧控制系统解耦设计[J].东北电力技术,2004,25(5):1-3.
[8]林永君,管志敏,彭钢,等.基于自抗扰控制的循环流化床锅炉床温系统的研究[J].热能动力工程,2010,25(5):514-516.
[9]Yukitomo M,Baba Y,Shigemasa T,et al.A model driven PID control system and its application to chemical processes[C]//Pennsylvania,USA:Proceeding of SICE Annual Conference,2002(4):2656-2660.

