基于SVM的汽车涂装线设备故障诊断

叶永伟，任设东，陆俊杰，杨　超

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)

基于SVM的汽车涂装线设备故障诊断

叶永伟，任设东，陆俊杰，杨超

(浙江工业大学 特种装备制造与先进加工技术教育部重点实验室，浙江 杭州 310014)

摘要：针对汽车涂装线设备故障无法及时发现和排除的困难，提出基于支持向量机的汽车涂装线设备故障诊断方法.该方法采用统计学习理论中结构风险最小化原则，克服了传统渐进理论机器学习算法的不足，适用于有限样本下模式识别问题，使预测结果更准确.依据烘房加热系统监测参数和故障类型构建SVM分类器，并采用交叉验证网格搜索法寻优各分类器的核参数及惩罚参数，建立SVM故障诊断模型；将PCA降维后的样本参数进行充分仿真训练，仿真结果表明该方法能够有效地对设备故障进行分类.

关键词：故障诊断；支持向量机；参数寻优；加热系统

Fault diagnosis for automobile coating equipment based on SVM

YE Yongwei, REN Shedong, LU Junjie, YANG Chao

(Key Laboratory of Special Purpose Equipment and Advanced Manufacturing Technology, Ministry of Education,

Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:Aiming at the difficulty in discovering and eliminating the system faults of automobile coating equipment promptly, a new method of fault diagnosis based on SVM was proposed. The method was created by the structural risk minimization principle in the statistical learning theory, which overcame the weakness of the traditional learning method in asymptotic theory. And it was suitably used in pattern recognition with finite samples and made the output more precise. The classifiers were also structured according to the equipment monitoring parameters and fault types of the heating system. The optimal kernel parameters and punished parameters were searched by the cross validation grid search method in order to establish the SVM model for fault diagnosis. The samples of dimension reducing by the PCA were then taken into training in the model. It was finally reveals by the simulation experiment that it can successfully and precisely accomplish the fault diagnosis with the SVM method.

Key words:fault diagnosis; support vector machines; parameter optimization; heating system

汽车涂装设备运行参数空间重叠，维数大，具有耦合性，需对涂装线各设备运行状态进行监控并对潜在故障及时诊断以确保设备稳定运行.在支持向量机(Support vector machines，SVM)[1]基础上，设计一种基于SVM的设备故障诊断方法.SVM方法采用统计学习理论(Statistical learning theory，SLT)中结构风险最小化算法，尤其适合设备故障诊断中样本数据有限的情况[2]，它克服了传统学习方法易产生过学习状态或只能得到局部极值的缺陷，使测试结果更接近实际值[3].基于该方法，对汽车涂装线设备故障频发的问题进行研究，首先分析SVM模型结构和算法原理，以及模型核参数和惩罚参数对训练、预测精度的影响，并以烘房加热系统为例，构建SVM分类器进行仿真实验.同时，为验证PCA降维数据的可靠性，将原始监测数据与降维后数据对比试验.仿真结果验证了SVM方法在故障诊断中的有效性，同时也说明PCA降维的可行性.

1设备故障诊断方法

机械设备故障诊断主要包括以传感器监测技术和动态测试技术为基础的常规故障诊断，及以人工智能技术为核心的智能诊断[4-6].随着人工智能技术的发展，故障诊断智能化已成为主要的发展方向，并以专家系统和基于机器学习的诊断方法最具代表.专家系统能有效利用领域专家长期积累的经验建立知识库，采用智能算法模拟人类专家推理决策过程，从而实现对故障设备的诊断.专家系统存在的主要问题是领域知识获取难，运行速度慢[7].不同于专家系统依赖于经验知识库，机器学习方法能够从变化的环境中学习新知识，实现自身的发展[8].人工神经网络(ANN)作为机器学习的典型性算法，已经在故障诊断领域开展较多的研究并得到实际的应用.ANN不需要知识工程师总结、消化领域专家知识，只需将已解决的问题案例进行网络学习，并且具有较高的非线性、高度容错性及分布并行处理能力.但ANN算法基础是基于渐进理论的传统统计学，只有在样本数目趋于无穷时，预测性能才有理论上的保证，并且在训练过程中容易陷入局部最优.

基于统计学习理论发展起来的支持向量机克服了上述缺陷，与人工神经网络相比，支持向量机结构更简单，泛化能力强，更适合于解决故障诊断等实际有限样本问题.支持向量机的研究成果，已经广泛应用于模式识别、函数回归、概率估计等领域，并且自身仍在不断地发展中，主要包括[9-12]：针对传统SVM只处理二分类问题，研究分解法、决策树分类法等多状态分类方法，使SVM分类更具实用性；在标准SVM算法基础上，通过增加函数项、系数等方法，研究SVM变型算法，拓展SVM的应用范围；进一步研究核函数选择及核参数优化方法，提高SVM学习效率和测试精度.

2SVM理论模型及参数寻优

Vapnik等学者对统计学习理论(SLT)经过多年研究，系统分析了机器学习问题，于1995年全面总结其研究内容和思想.支持向量机(SVM)是在SLT基础上而发展的一种新的机器学习方法，应用于有限样本下函数分类及回归问题[13-14].在传统机器学习方法理论研究遭遇瓶颈时，以SLT为基础的支持向量机研究吸引了国内外学者的关注.

2.1SVM理论模型

假定大小为l的训练样本集{(xi,yi),i=1,2,…,l}，分为两类，即xi∈RN属于第1类，则yi=1，如果归于第2类，则yi=-1；如果存在分类超平面，即

w·x+b=0

(1)

使得

(2)

则称训练集线性可分，式中w·xi为向量w∈RN与xi∈RN的内积，并构造符号判断函数为

y(x)=sign(w·x+b)

(3)

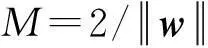
(4)

式中：C为惩罚参数，指定对错误分类的惩罚程度.对式(4)采用拉格朗日法求解二次规划问题，即

(5)

式中：αi，βi分别为拉格朗日乘子，求解拉格朗日优化算子，并带入式(4)得到最优化对偶问题，即

(6)

当所构建分类平面为非线性超平面时，需要引入非线性函数φ(·)，通过将样本集映射到高维线性特征空间，在该空间中构造超平面以得到最优化对偶问题和判别函数，即

(7)

式中:K(xi·xj)=φ(xi)·φ(xj)为核函数，判别函数为

(8)

2.2核参数及惩罚参数寻优

统计学习理论系统研究了各种类型指示函数集，总结了实际风险(实际误差)和经验风险(训练误差)之间的关系，即结构风险最小化原则为

R(w)≤Remp(w)+W(h/n)

(9)

式中：R(w)为实际风险；Remp(w)为经验风险；W(h/n)为误差置信区间；h为函数集VC维数；n为样本数.

结构风险最小化要求机器学习过程中协调经验风险和误差置信区间，提高学习泛化能力.也即当核函数过于复杂，虽然能使经验风险最小，但是增大了置信区间，使得实际风险反而变大.这也很好说明了为什么很多机器学习方法在样本训练时精度很高，甚至零误差，但是预测结果并不理想，出现机器过学习状态.因此，选择合适的核函数和核参数及惩罚参数是建立SVM分类器的关键.

常用核函数有多项式类型核函数、多层感知器类型核函数、傅里叶核函数及本研究将采用的高斯径向基核函数.大量试验证明高斯径向核函数的支持向量机具有良好的学习性能，在函数分类和回归问题中取得了良好效果[15].因此，本研究首先通过仿真实验分析核参数和惩罚参数对SVM训练和测试精度的影响.

高斯核函数表达式为

(10)

其中γ为核宽度系数.

仿真试验1以模式识别中典型的双螺旋数据进行学习，双螺旋数据由极坐标系下方程r=θ和r=-θ两条曲线相互缠绕而成.现以每条曲线上随机选取288个数据点，其中取96个样本点作为训练样本，其余作为测试样本.

采用高斯核函数支持向量机，通过调整核参数系数γ值，研究分析γ对分类器训练精度、测试精度及支持向量数目(NSV)的影响.同时为增加实验仿真对比度，采用标准C-SVC和Nu-SVC两类高斯核函数支持向量机算法进行对比仿真试验，得到如图1～3所示曲线图.

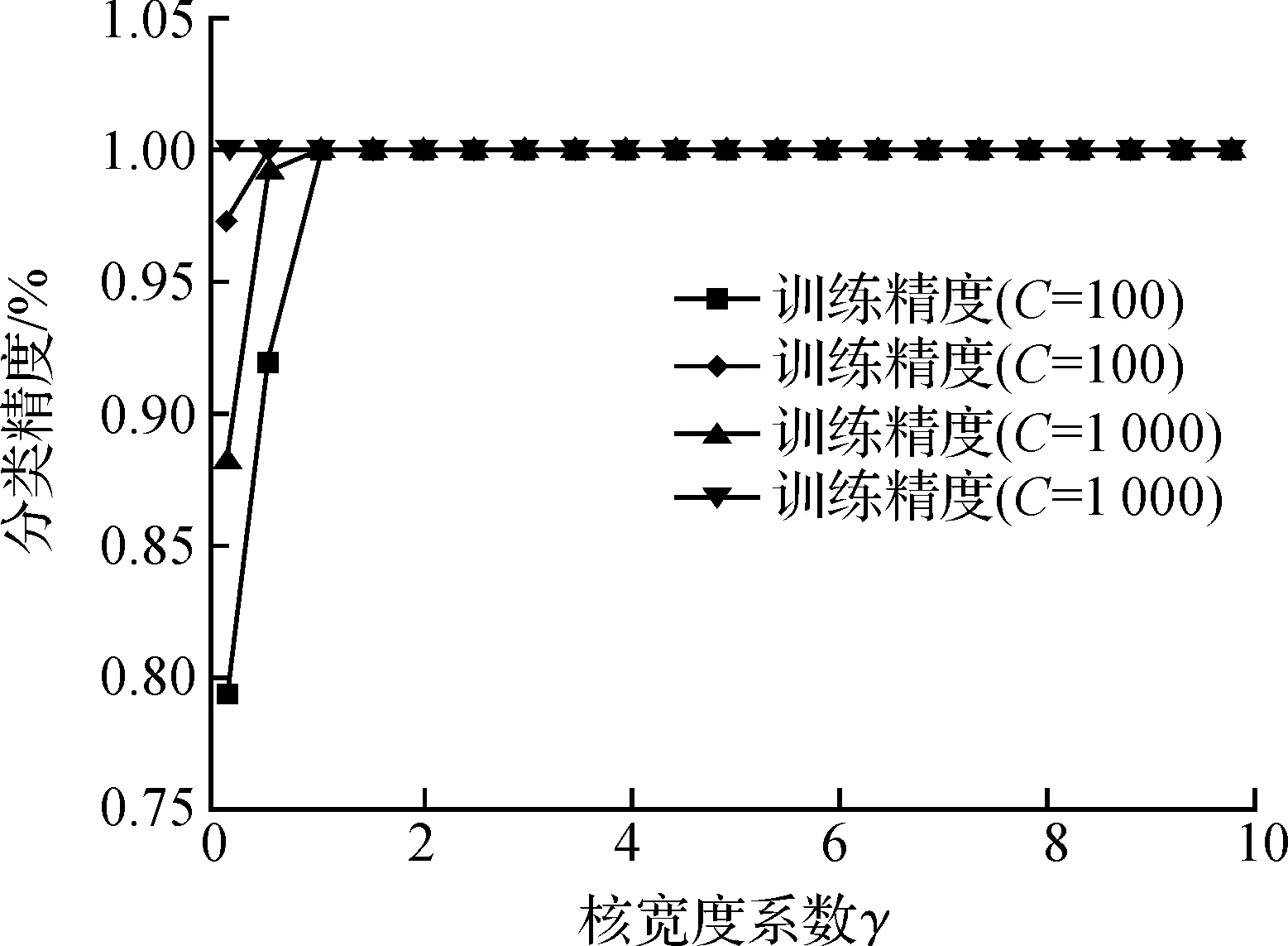
图1　训练精度和测试精度随γ变化曲线(C-SVC)Fig.1　Curves of Training and testing withγ(C-SVC)

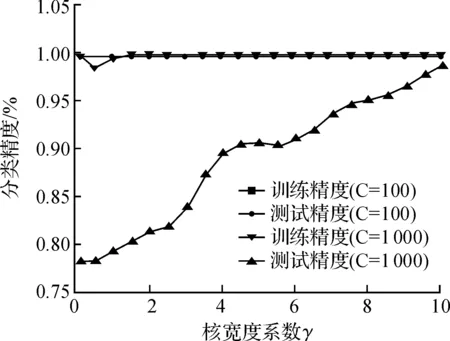
图2　训练精度和测试精度随γ变化曲线(Nu-SVC)Fig.2　Curves of Training and testing withγ(Nu-SVC)

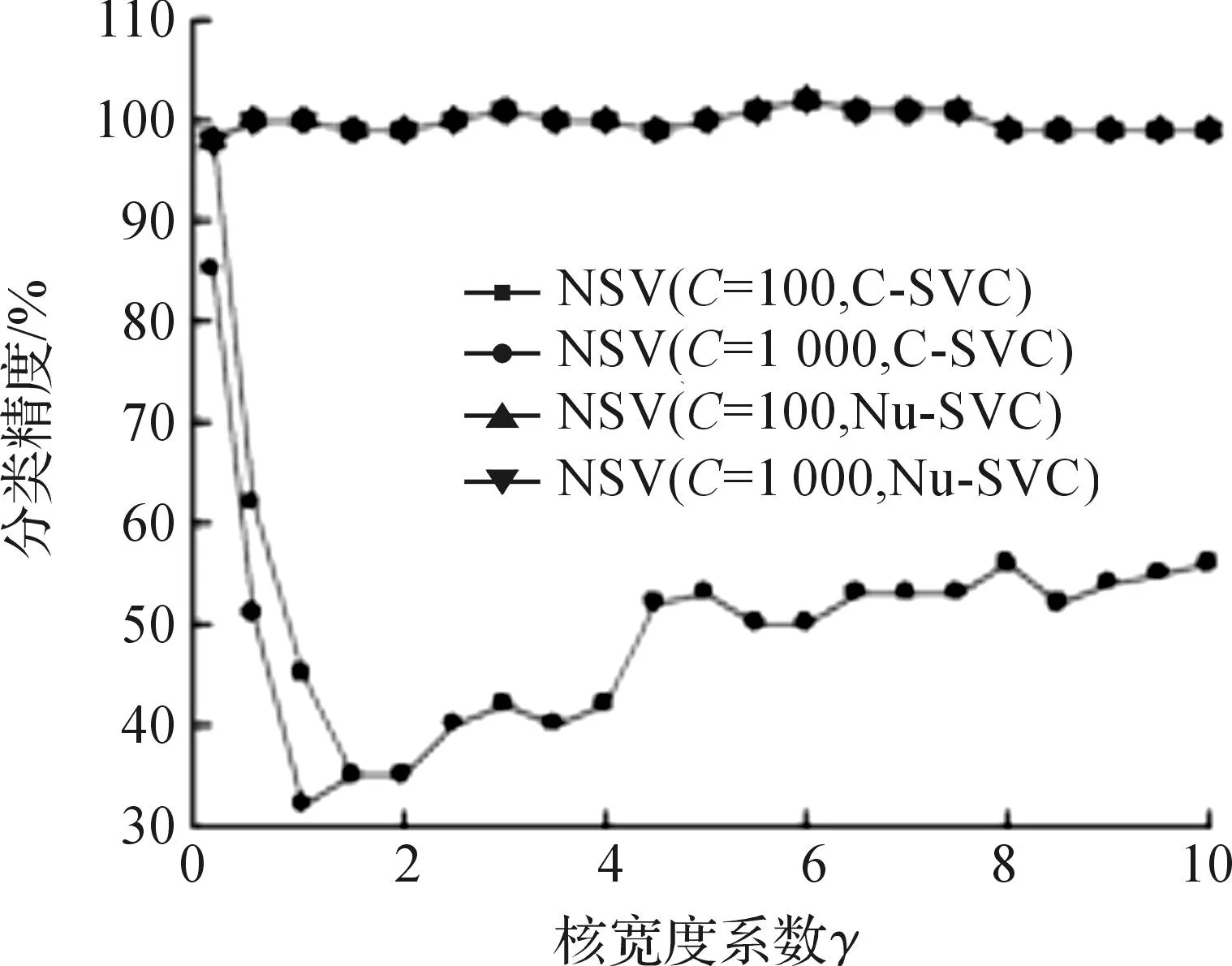
图3　支持向量数目随γ变化曲线(C-SVC和Nu-SVC)Fig.3　Curves of NSV withγ(C-SVC and Nu-SVC)

由图1，3知：在C-SVM算法中，当C=100，γ=0时，分类器训练精度80%左右，支持向量数目(NSV)接近100，推广能力不是很好；当γ取值接近1时，此时算法的训练精度和预测精度都较高，并且NSV接近30个左右，分类器具有较好的推广能力.

由图2，3知：Nu-SVM算法虽然预测精度不低，但其支持向量数目变化不大，100个左右，分类器的推广能力不如标准支持向量机.

仿真试验2仿真数据采用与仿真试验1中相同的样本集和核函数，通过调整惩罚参数C值，研究分析C对分类器训练精度、测试精度和支持向量数目的影响，得到图4～6仿真曲线.

图4　训练精度和测试精度随C变化曲线(C-SVC)Fig.4　Curves of Training and testing with C (C-SVC)

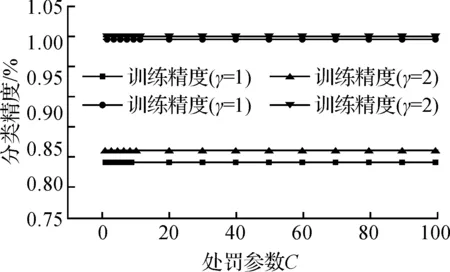
图5　训练精度和测试精度随C变化曲线(Nu-SVC)Fig.5　Curves of Training and testing with C (Nu-SVC)

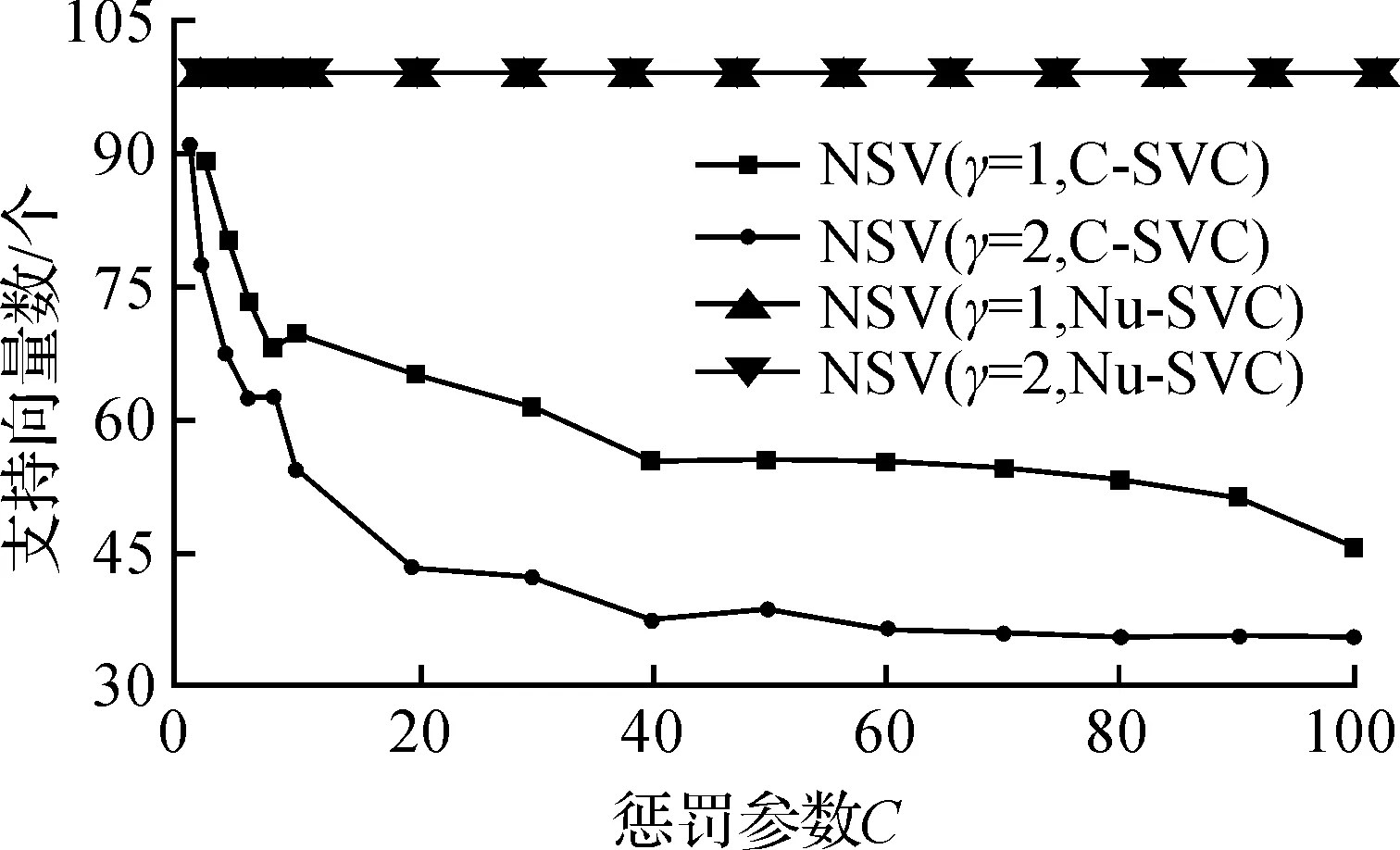
图6　支持向量数目随C变化曲线(C-SVC和Nu-SVC)Fig.6　Curves of NSV with C (C-SVC and Nu-SVC)

由图4，6知：C-SVC算法中γ取值的两种情况，其曲线变化趋势是一致的，当C取较小值时，训练精度不高，并且支持向量个数多；但随着C值增加，样本集训练和测试精度都基本可以达到100%，同时支持向量数值减小并趋于稳定.

由图5，6知：Nu-SVC算法中γ取值的两种情况下，其分类精度和NSV个数基本保持恒定状态，说明该算法的支持向量机对惩罚参数C不敏感，机器处于过学习状态，且算法泛化能力低.

统计学习理论针对SVM核参数γ和惩罚参数C的组合优化问题在理论上还没有形成一种全面的优化方案，在实际应用中，参数优化主要包括经验法、交叉验证法、网格搜索法、统计法、VC维法等寻优方法，笔者在SVM建模中采用交叉验证网格搜索法进行参数的寻优.

3SVM在烘房设备故障诊断中的应用

汽车涂装线烘房系统主要由燃烧加热、热风循环和废气处理三个子系统组成，以烘房系统中最关键的燃烧加热子系统为研究对象，建立起基于SVM的汽车涂装线烘房设备故障诊断模型，为涂装设备后续的故障诊断奠定基础.

3.1加热系统设备状态特征提取

叶永伟等对汽车涂装线特征参数进行了PCA降维研究[16]，通过PCA对样本参数进行处理后，将原17维输入样本约减为8个主成分，12维监测空间参数，降低了输入样本的维数，利于学习系统对故障类型正确分类.约减后的12维参数为：风机振动烈度(F1)，加热温度(TW)，轴瓦温度(T1)，风机出口压力(PS3)，调节阀压力(PS1)，风机转速(n1)，电机电流(I).其中，按照风机振动烈度大小，F1划分为F1.1(<0.4f，f为风机基频)，F1.2(0.4f～0.49f)，F1.3(0.5f)，F1.4(0.51f～0.99f)，F1.5(f)，F1.7(3f～4f).

根据专家经验库和现场设备运行状况，燃烧加热系统设备运行状态标定如下：

风机状态包括正常运行(S0)，转子动不平衡(S1)，转子转轴不对中(S2)，油膜出现涡动(S3)，动、静件碰摩严重(S4)；燃烧器状态包括正常运行(S5)，燃气阻塞(S6)，燃油系统故障(S7)；调节阀状态包括正常运行(S8)，调节阀阻塞(S9)；电机状态包括正常运行(S10)，电流脉动(S11)，共12个状态模式.

3.2SVM分类器构建

在最初分类问题上，支持向量机主要用于简单的二值分类问题，然而在机电系统故障诊断领域，故障征兆和类型通常不是简单的二值分类问题，是一个复杂的多类识别问题.研究采用一对余类的方法构建燃烧加热系统故障状态分类器.

一对余类分类器构造思想是将k种分类状态中第i类作为一类，其余k-1类视为另一类，将复杂的多类问题转化为简单的二值分类问题处理.因此对于烘房燃烧加热系统的12种状态，构造11个两类分类器的子分类器，将某一种状态样本和其余状态样本作为某一子分类器的两类输入，并用+1和-1标识其输出的两种状态结果，构建的分类器表示为SVM(n)，n=0，1，2，…，10.

3.3模型仿真与分析

现场实验测得120组数据样本，并对其进行PCA处理得到实测数据12维的前8个主成分数据样本.选取72组作为训练样本，每种状态6组；其余作为测试样本，每种状态4组样本，由于篇幅有限，部分数据样本如表1所示.同时，为了验证文献[16]PCA降维的有效性，仿真实验将原始监测17维参数及降维后的12维参数进行对比分析验证.

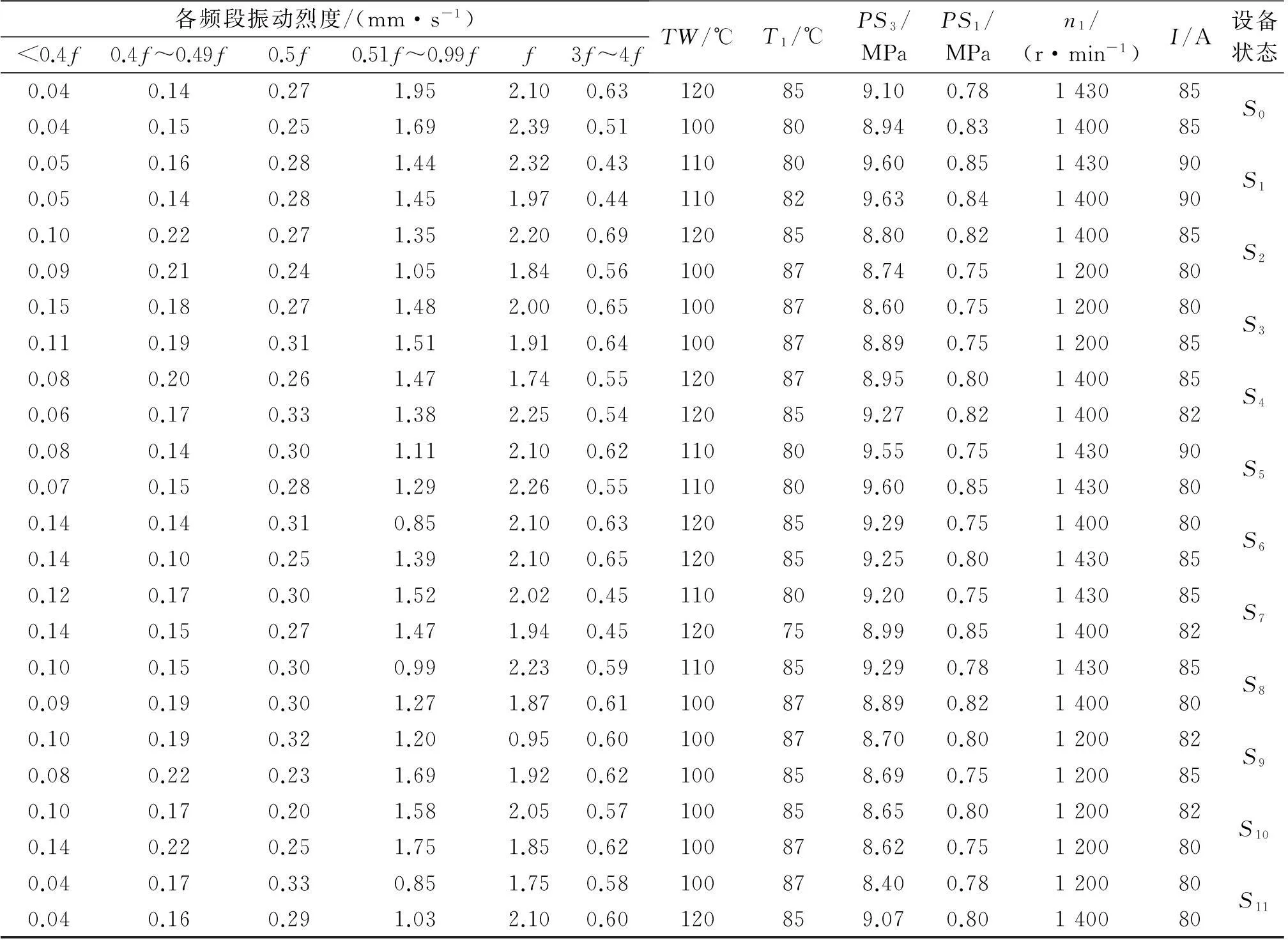
表1　烘房加热系统监测参数

3.3.1模型核参数及惩罚参数的确定

研究采用交叉验证网格搜索法确定核参数γ和惩罚参数C值，并采用指数增长方式，快速确定(C，γ)的范围，其大致范围为：C=2-5，2-3，…，215，γ=2-15，2-13，…，23.

将范围内数据两两配对，组成110个参数对，并对参数对进行V=110重交叉验证.即将样本集分为V个子集，将V-1个子集作为训练集，测试剩下的一个子集，这样每个子集都可以成为测试集，以预测样本集中的每个子集.该方法可以获得比较精确的(C，γ)，仿真实验得到如表2中各分类器的最优参数值.

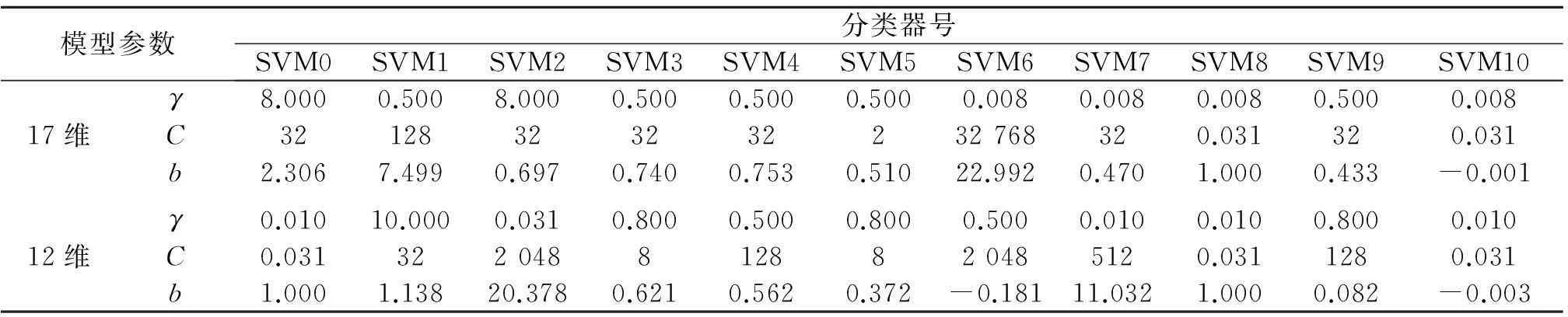
表2　分类器优化参数

3.3.2模型仿真实验与分析

确定各分类器核参数和惩罚参数后，建立基于SVM的多模式故障测试模型，将样本特征参数进行训练和测试，得到试验仿真结果.如图7所示为各分类器训练、测试精度仿真结果，及图8所示为各分类器的支持向量个数，图7，8中横坐标为表2中分类器号的缩写.

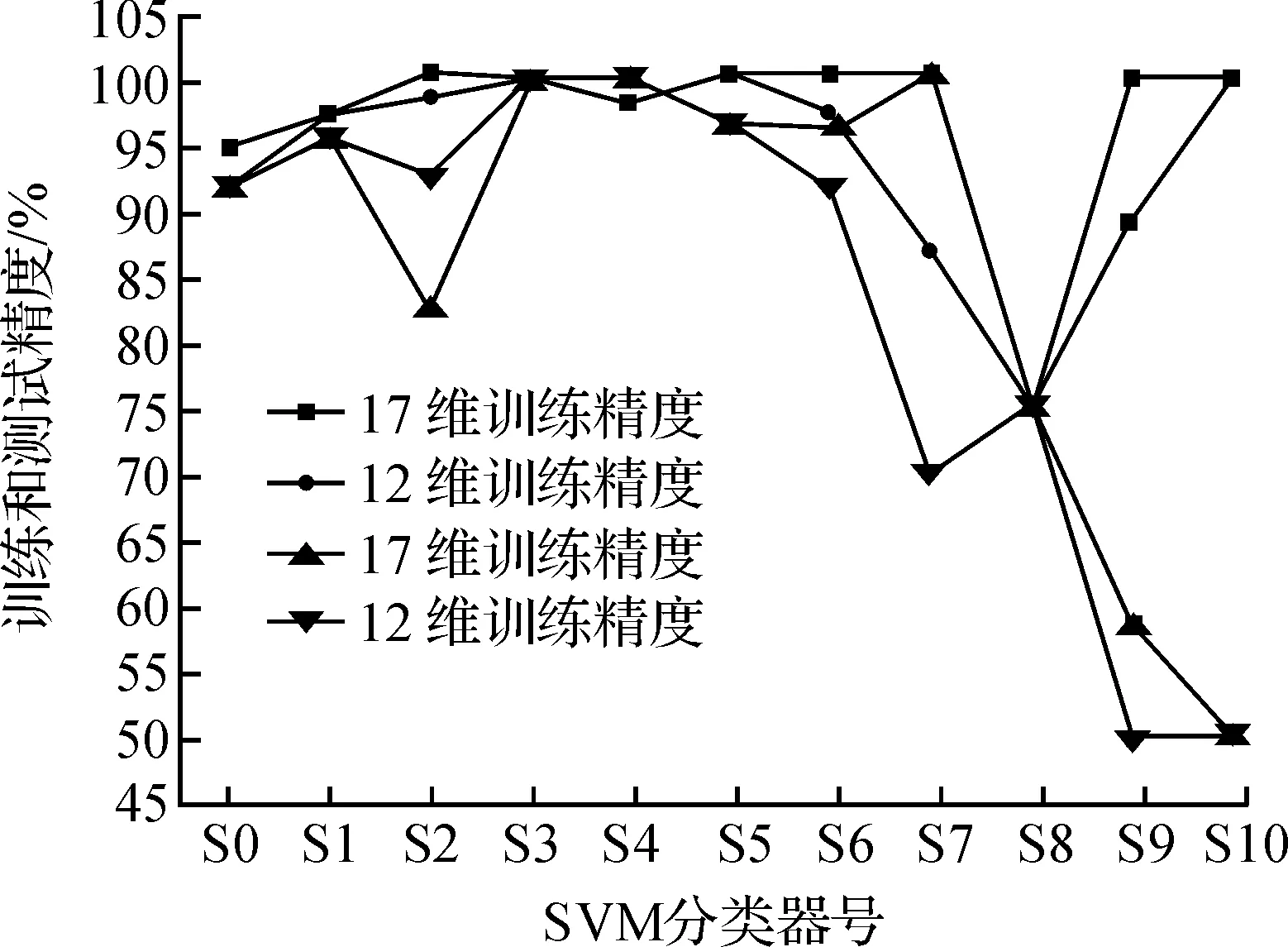
图7　各分类器训练和测试精度Fig.7　Training and testing precision of classifiers

图8　各分类器支持向量数Fig.8　NSV of classifiers

由图7知：监测参数空间17维和12维时样本训练精度基本一致，其精度达到85%以上，测试精度基本在75%以上；S2分类器(即SVM2)中，参数空间为12维的样本测试精度高于17维的样本测试效果，而随着样本数的减少，两者的测试分类精度都呈下降趋势.

在保证训练和预测精确度前提下，支持向量数少，则说明该分类器具有较好泛化能力.图8中，虽然分类器S6，S7的支持向量数目最小，但其对应的分类精度不高；而参数空间12维的S3分类器训练和预测精度都达到90%以上，同时支持向量数少，具有好的推广能力.

4结论

研究采用SVM方法建立汽车涂装线设备的故障诊断模型，并对烘房加热系统监测数据进行仿真训练，结果表明：利用交叉验证网格搜素法可以快速地确定各分类器的最优核参数γ和惩罚参数C，并且测试结果也表明了原始17维特征参数的分类准确率和经PCA降维后的12维参数的分类准确率相当，在SVM2中后者的准确率甚至超过了前者.因此，研究结果说明了SVM方法在设备故障分类中的可行性，同时验证了降维方法在预测模型中的正确性.此研究将为有限故障样本下的汽车涂装线设备故障诊断提供一种新的方法.

参考文献：

[1]张学工.统计学习理论的本质[M].北京：清华大学出版社，2000.

[2]袁胜发，褚福磊.支持向量机及其在机械故障诊断中的应用[J].振动与冲击，2007，26(11)：29-35.

[3]张学工.关于统计学习理论与支持向量机[J].自动化学报，2000，26(1)：36-46.

[4]张萍，王桂增，周东华.动态系统的故障诊断方法[J].控制理论与应用，2000，17(2)：153-158.

[5]周东华，胡艳艳.动态系统的故障诊断技术[J].自动化学报，2009，35(6)：748-758.

[6]李红卫，杨东升，孙一兰，等.智能故障诊断技术研究综述与展望[J].计算机工程与设计，2013，26(2)：632-637.

[7]李增芳.基于人工智能和虚拟仪器技术的发动机故障诊断专家系统研究[D].杭州：浙江大学生物系统工程与食品科学学院，2004.

[8]THUKARAM D, KHINCHA H P, VIJAYNARASIMHA H P. Artificial neural network and support vector machine approach for locating faults in radial distribution systems [J]. IEEE Transaction on Power Delivery，2005，20(2)：710-721.

[9]罗亦泳，张豪，张立亭.基于遗传支持向量机的多维灰色变形预测模型研究[J].浙江工业大学学报，2010，38(1)：79-83.

[10]常甜甜.支持向量机学习算法若干问题的研究[D].西安：西安电子科技大学应用数学系，2010.

[11]顾亚祥，丁世飞.支持向量机研究进展[J].计算机科学，2011，38(2)：14-17.

[12]丁世飞，齐丙娟，谭红艳.支持向量机理论与算法研究综述[J].电子科技大学学报，2011,40(1)：2-10.

[13]YANG Xiaowei, TAN Liangjun, HE Lifang. A robust least squares support vector machine for regression and classification with noise[J]. Neurocomputing，2014，140(9)：41-52.

[14]PANTELIS B, SERGIOS T, CHARALAMPOS M, et al. Complex support vector machines for regression and quaternary classification[J]. IEEE Transactions on Neural Networks and Learning System, 2015，26(6)：1260-1274.

[15]林升梁，刘志.基于RBF核函数的支持向量机参数选择[J].浙江工业大学学报，2007，35(2)：163-167.

[16]叶永伟，刘志浩，黄利群.基于PCA的汽车涂装线设备信号特征提取[J].仪器仪表学报，2011，32(10)：2363-2370.

(责任编辑：刘岩)

文章编号：1006-4303(2015)06-0670-06

中图分类号：TP391

文献标志码：A

作者简介：叶永伟(1964—)，男，浙江义乌人，副教授，主要从事机电系统智能控制方向研究，E-mail: yyw@zjut.edu.cn.

基金项目：浙江省自然科学基金资助项目(LY12E05025)

收稿日期：2015-09-17