混凝土氯离子扩散系数预测的两步解析法

周欣竹，张　坚，郑建军，章丹王

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

混凝土氯离子扩散系数预测的两步解析法

周欣竹，张坚，郑建军，章丹王

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

摘要：针对现有混凝土氯离子扩散理论模型的不足，提出了混凝土氯离子扩散系数预测的两步解析法.将混凝土看成一种是由骨料、水泥石基体和界面组成的三相复合材料，基于非均匀界面模型，估算出水泥石基体和界面的水灰比、水化度和氯离子扩散系数，然后根据微分有效介质方法，提出了混凝土氯离子扩散系数的简单解析解.做了一组混凝土氯离子扩散试验，通过与试验结果比较初步证实了所提出的两步解析法的有效性.最后通过敏感性分析量化了影响混凝土氯离子扩散系数的两个主要因素，结果表明：随着水灰比增大或骨料体积分数减小，混凝土氯离子扩散系数增大.

关键词：混凝土；氯离子扩散系数；两步解析法；界面；水灰比；骨料体积分数

A two-step analytical method for predicting the chloride diffusivity of concrete

ZHOU Xinzhu, ZHANG Jian, ZHENG Jianjun, ZHANG Danwang

(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:In view of the defects in existing theoretical models for the diffusion of chloride ions in concrete, a two-step analytical method is presented in this paper for the chloride diffusivity of concrete. Concrete is considered to be a three-phase composite material, composed of aggregates, bulk cement paste, and interfacial transition zone (ITZ). Based on an inhomogeneous ITZ model, the water/cement ratios, degrees of hydration, and chloride diffusivities of bulk cement paste and ITZ are estimated. According to the differential effective medium approach, an simple analytical solution for the the chloride diffusivity of concrete is then derived. A diffusion test of concrete was conducted. The validity of the developed two-step analytical method is verified in comparison with the experimental results. Finally, two main factors that affect the chloride diffusivity of concrete are quantified through a sensitivity analysis. The results show that the chloride diffusivity of concrete increases as the water/cement ratio increases or the aggregate volume fraction decreases.

Key words:concrete; chloride diffusivity; two-step analytical method; ITZ; water/cement ratio; aggregate volume fraction

氯盐环境中钢筋混凝土结构的失效主要归结为氯离子扩散引发内部钢筋锈蚀，因此，决定钢筋混凝土结构服役寿命的一个关键因素是混凝土氯离子扩散系数[1-3].从微观结构水平上看：混凝土是一种典型的多尺度、多相及多孔材料，它包括各种尺度的孔隙结构、水化产物、缺陷与裂缝、未水化水泥颗粒和粗细骨料[4]，氯离子通过孔隙和裂缝进入到混凝土内部，一旦钢筋表面的氯离子含量达到临界值，钢筋开始生锈.目前，测定混凝土氯离子扩散系数的主要方法包括RCM法、电量法、NEL法和自然扩散法，试验测定不仅要求一定的试验装置，而且需要较长的时间.混凝土氯离子扩散系数的理论预测基于Fick第二定理[5]，主要方法包括一般有效介质方法[6]、微分有效介质方法[7]和复合圆模型[8-9]等，前两种方法主要适用于两相介质，而实际混凝土还应该考虑骨料与水泥石基体之间的界面层[8]，第三种模型虽然可以处理界面层，但界面层氯离子扩散系数往往通过试验数据反算而获得，不便于工程应用.

在前人工作的基础上，笔者先根据混凝土界面微观结构模型估计水泥石基体和界面层氯离子扩散系数，再应用微分有效介质近似方法导出混凝土氯离子扩散系数，在笔者方法的有效性得到试验结果的初步证实后，评价了两个主要因素对混凝土氯离子扩散系数的影响.

1水泥石基体和界面孔隙率

1.1水泥石基体和界面水灰比

在预测混凝土氯离子扩散系数时，通常将界面层看成是有别于水泥石基体和骨料的独立相.尽管从统计的观点来看，水泥石基体中的水泥颗粒分布均匀，但由于骨料边壁效应的存在，界面层上的水泥颗粒分布呈现明显的不均匀性，形成一个低强度、高孔隙率、具有一定梯度分布的区域.对于普通混凝土，界面层厚度h一般在0.01～0.05 mm之间，取其均值0.03 mm.根据Zheng等的界面层模型[10]，界面层上离骨料表面x处的水泥颗粒分布密度f(x)可表示成

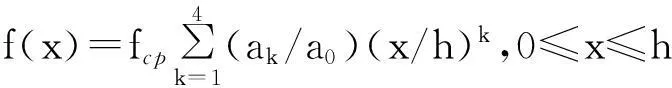
(1)

式中：fcp为水泥石基体的水泥颗粒分布密度，它可以通过界面层和水泥石基体中水泥体积之和等于混凝土中水泥总体积而求得；经验系数ak(k=1,2,3,4)通过与试验结果比较而获得，它们与混凝土总体水灰比(w/c)0之间的关系[7]为

a1=4.670-5.228(w/c)0

(2)

(3)

(4)

(5)

而a0为上述四个经验系数之和.这样，水泥石基体的水灰比(w/c)cp为

(6)

式中ρc为水泥密度.界面层中任一点x处的局部水灰比(w/c)itz为

(7)

这样，界面层的平均水灰比(w/c)itz,a为

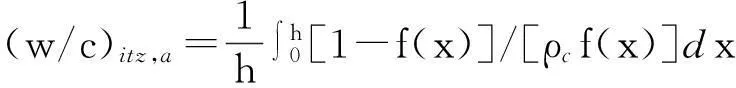
(8)

1.2水泥石基体和界面孔隙率

根据试验结果[11]，水泥石水化度与水灰比(w/c)和养护时间t的关系为

α=(8.63ln(t)+68.3)exp[-(0.923ln(t)+

10.1)/(w/c)]

(9)

这样，水泥石基体的水化度αcp和界面区水化度αitz分别为

αcp=(8.63ln(t)+68.3)exp[-(0.923ln(t)+

10.1)/(w/c)cp]

(10)

αitz=(8.63ln(t)+68.3)exp[-(0.923ln(t)+

10.1)/(w/c)itz,a]

(11)

根据Powers模型[12]，水泥石孔隙率可以表示成水灰比(w/c)和水化度α的函数，即

(12)

则水泥石基体和界面层的孔隙率φcp和φitz分别为

(13)

(14)

2混凝土氯离子扩散系数

根据Garboczi和Bentz模型[13]，水泥石氯离子扩散系数D可以表示成

D=D0[0.001+0.07φ2+

1.8H(φ-φc)(φ-φc)2]

(15)

式中：φc为临界孔隙率，取0.18；D0为孔溶液氯离子扩散系数；H(x)为阶跃函数，当x>0时，H=1，否则H=0.这样，水泥石基体和界面层的氯离子扩散系数Dcp和Ditz分别为

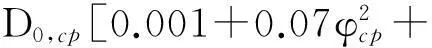
1.8H(φcp-φc)(φcp-φc)2]

(16)

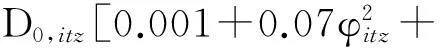
1.8H(φitz-φc)(φitz-φc)2]

(17)

式中D0,cp和D0,itz分别为水泥石基体和界面层孔溶液氯离子扩散系数.根据Garboczi和Berryman提出的微分有效介质方法[7]，混凝土氯离子扩散系数[14]为

(18)

式中系数a，b，c与骨料体积分数Vagg之间的关系为

a=0.456-0.50Vagg

(19)

b=4.69-5.04Vagg

(20)

c=-0.129+1.06Vagg

(21)

这样，就可以根据式(18)计算混凝土氯离子扩散系数.

3试验验证与讨论

3.1氯离子扩散试验

为了验证上述两步解析法的有效性，我们设计并完成了一组不同骨料体积分数的混凝土氯离子扩散试验.该试验采用浙江钱潮水泥厂生产的P·O 42.5普通硅酸盐水泥.细骨料选用河砂，表观密度为2 630 kg/m3，含水率为0.30%，吸水率为1.41%.粗骨料选用碎石，表观密度为2 750 kg/m3，含水率为0.30%，吸水率为1.13%.粗、细骨料尺寸采用富勒级配，最大骨料尺寸为19 mm，最小骨料尺寸为0.15 mm.搅拌水取自pH值为6.5的市区自来水，养护水采用饱和Ca(OH)2溶液.为减少其他杂质对混凝土氯离子扩散的影响，采用NaCl质量分数≥98.5%的精制盐来配制饱盐盐水.混凝土水灰比为0.55，骨料体积分数分别为0，0.55，0.65，0.75.采用圆柱形试件，试件尺寸为φ100 mm×100 mm.试件浇筑完成后先在温度为(20±5) ℃的环境中静置1～2 d，拆模后立即将试件浸没在盛有Ca(OH)2饱和溶液的水池中，养护温度为(20±2) ℃，养护时间为28 d.试验中采用NEL法测定混凝土氯离子扩散系数[15].

3.2理论预测与试验结果比较

根据上述方法所测得的混凝土氯离子扩散系数见图1.在应用式(18)计算混凝土氯离子扩散系数时，水泥石基体和界面层孔溶液氯离子扩散系数需要通过试验校正获得.当骨料体积分数为零时，所测得的水泥石氯离子扩散系数为9.4 μm2/s，通过反算求得水泥石基体孔溶液氯离子扩散系数为140 μm2/s.当骨料体积分数为0.55时，所测得的混凝土氯离子扩散系数为6.3 μm2/s，通过反算求得界面层孔溶液氯离子扩散系数为509 μm2/s.有了这两个参数就可以利用式(15)计算混凝土氯离子扩散系数，结果如图1所示.从图1可以看出：理论预测与试验结果良好吻合，当骨料体积分数为0.65和0.75时，它们之间的相对误差分别为1.61%和0.87%.因此，笔者所提出的混凝土氯离子扩散系数预测方法的有效性得到试验结果的初步验证.

3.3影响因素分析

由上述理论分析可知：影响混凝土氯离子扩散系数的主要因素包括水灰比和骨料体积分数，设D0,cp=140 μm2/s，D0,itz=509 μm2/s，由式(18)给出混凝土氯离子扩散系数与骨料体积分数之间的关系，结果如图2所示.该图表明，当骨料体积分数一定时，水灰比越大，混凝土氯离子扩散系数也越大，这是因为水灰比越大，水泥石基体和界面层中的孔隙率越大，氯离子越容易在混凝土中扩散.当水灰比从0.35增大到0.65时，骨料体积分数为0.55，0.65，0.75的混凝土氯离子扩散系数分别增大50%，59%，68%.图2还表明：当水灰比一定时，骨料体积分数越小，混凝土氯离子扩散系数越大，这主要归结于骨料的稀释效应和骨料边界的曲折性.当骨料体积分数从0.75减小到0.55时，水灰比为0.35，0.45，0.55，0.65的混凝土氯离子扩散系数分别减小36%，30%，24%，21%.

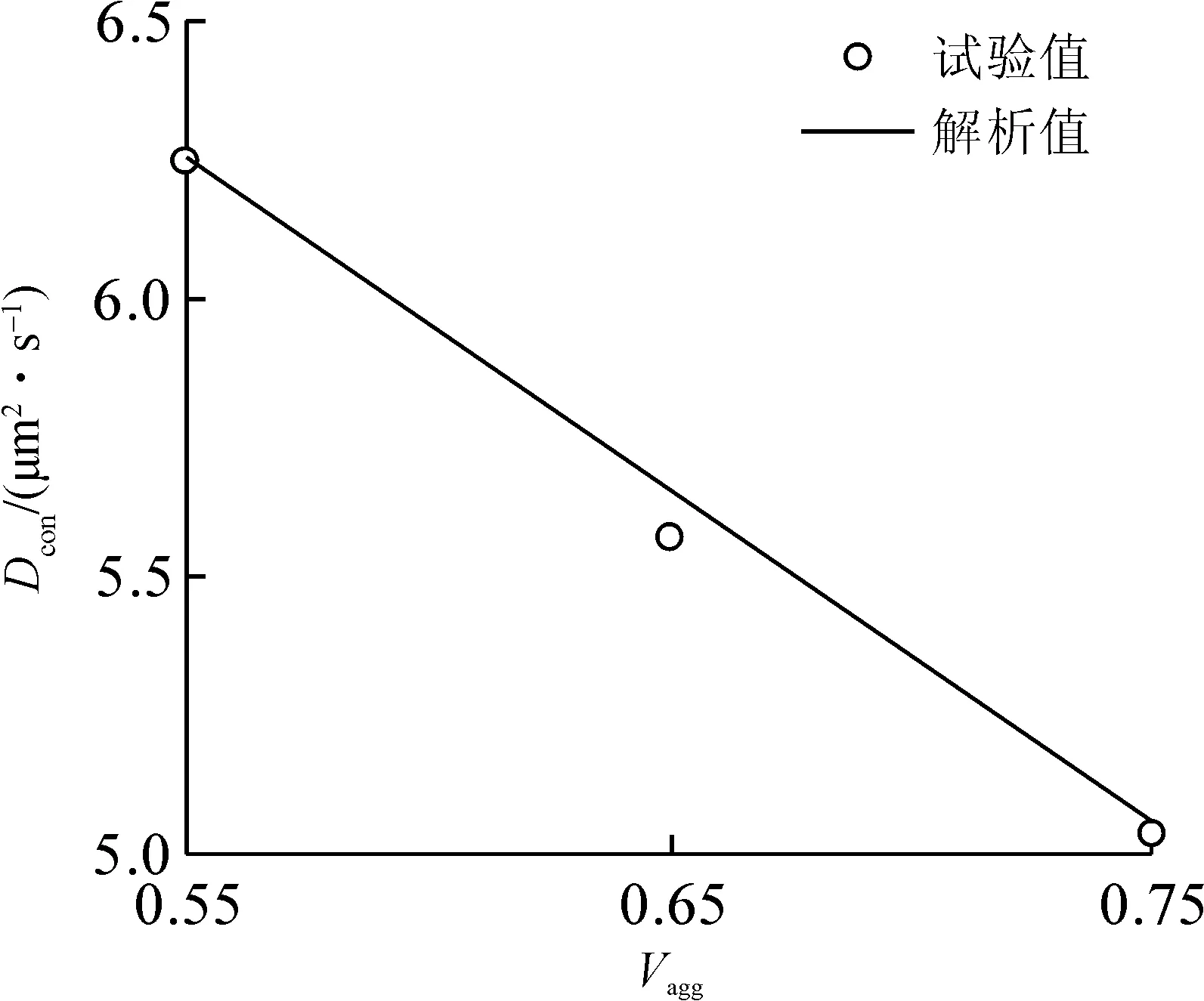
图1　理论预测与试验结果比较Fig.1　Comparison between theoretical predictions and experimental results

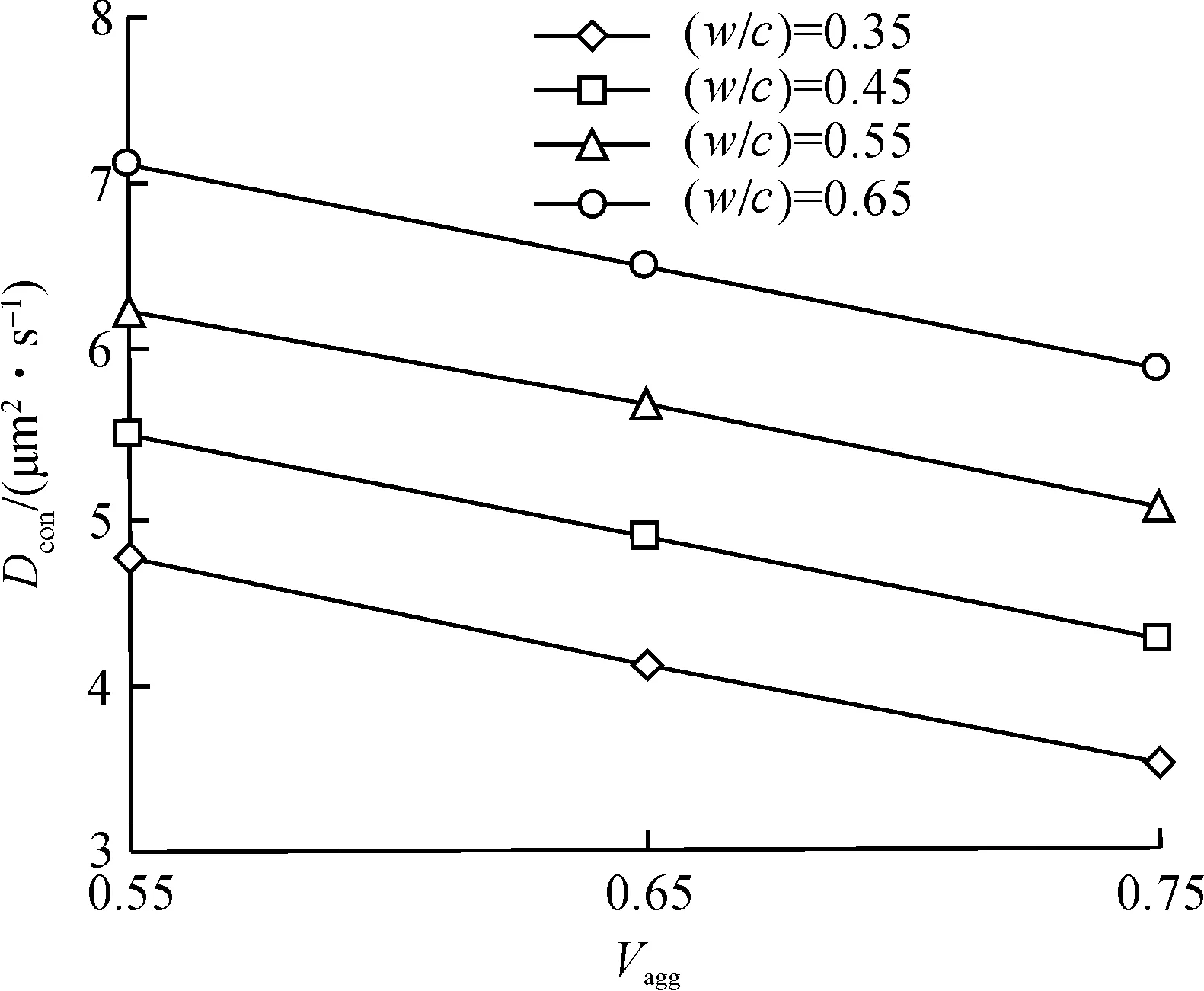
图2　不同水灰比混凝土氯离子扩散系数与骨料体积分数的关系Fig.2　Relationship between chloride diffusivity and aggregate volume fraction of concrete with different water/cement ratios

4结论

通过研究得出：1) 将非均匀界面模型与微分有效介质方法相结合，导出了混凝土氯离子扩散系数预测的两步解析法.2) 解析法与笔者试验结果良好吻合，该方法的有效性得到初步证实.3) 敏感性分析表明，混凝土氯离子扩散系数随着水灰比的增大而增大，当水灰比从0.35增大到0.65时，骨料体积分数为0.55，0.65，0.75的混凝土氯离子扩散系数分别增大50%，59%，68%，但骨料体积分数越大，混凝土氯离子扩散系数越小，当水灰比为0.35，0.45，0.55，0.65时，骨料体积分数为0.75的混凝土氯离子扩散系数比骨料体积分数为0.55的混凝土氯离子扩散系数分别小36%，30%，24%，21%.

参考文献：

[1]BENTZ D P, GARBOCZI E J, LAGERGREN E S. Multi-scale microstructural modeling of concrete diffusivity: identification of significant variables[J]. Cement, Concrete and Aggregates,1998,20(1):129-139.

[2]周欣竹,张海龙,郑建军.钢筋混凝土梁承载力退化的试验研究[J].浙江工业大学学报,2014,42(6):655-659.

[3]王建东,张俊芝,沈妙金,等.关于人工气候环境下混凝土梁中氯离子侵蚀规律的研究[J].浙江工业大学学报,2010,38(6):625-628.

[4]SUN Guowen, ZHANG Yunsheng, SUN Wei, et al. Multi-scale prediction of the effective chloride diffusion coefficient of concrete[J]. Construction and Building Materials,2011,25(10):3820-3831.

[5]SERGI G, YU S W, PAGE C L. Diffusion of chloride and hydroxyl ions in cementitious materials exposed to a saline environment[J]. Magazine of Concrete Research,1992,44(158):63-69.

[6]OH B H, JANG S Y. Prediction of diffusivity of concrete based on simple analytic equation[J]. Cement Concrete Research,2004,34(3):463-480.

[7]GARBOCZI E J, BERRYMAN J G. New effective medium theory for the diffusivity or conductivity of a muti-scale concrete microstructure model[J]. Concrete Science and Engineering,2000,2(6):88-96.

[8]ZHENG Jianjun, ZHOU Xinzhu. Prediction of the chloride diffusion coefficient of concrete [J]. Materials and Structures,2007,40(7):693-701.

[9]梁云滢,郑建军,丁建江.混凝土氯离子扩散系数预测的三相复合圆—格构模拟方法[J].浙江工业大学学报,2010,38(2):207-211.

[10]ZHENG Jianjun, WONG H S, BUENFELD N R. Assessing the influence of ITZ on the steady-state chloride diffusivity of concrete using a numerical model[J]. Cement and Concrete Research,2009,39(9):805-813.

[11]LAM L, WONG Y L, POON C S. Degree of hydration and gel/space ratio of high-volume fly ash/cement systems[J]. Cement and Concrete Research，2000,30(2000):747-756.

[12]HANSEN T C. Physical structure of hardened cement paste: a classical approach[J]. Materials and Structures,1986,19(6):423-436.

[13]BENTZ D P, GARBOCZI E J. Percolation of phases in a three-dimensional cement paste microstructure modal[J]. Cement and Concrete Research,1991,21(2/3):325-344.

[14]SONG H W, JANG J C, BYUN K J. An estimation of diffusivity of silica fume concrete[J]. Building and Environment,2007,42(3):1358-1367.

[15]LU Xinying. Application of the Nernst-Einstein equation to concrete[J]. Cement and Concrete Research,1997,27(2):293-302.

(责任编辑：陈石平)

文章编号：1006-4303(2015)06-0695-04

中图分类号：TU528.1

文献标志码：A

作者简介：周欣竹(1966—)，女，江苏南京人，教授，研究方向为混凝土材料与结构耐久性，E-mail：xzzhou66@hotmail.com.

基金项目：国家自然科学基金资助项目(51379188)

收稿日期：2015-03-27