RC Z形柱框架节点拟静力试验有限元分析

2016-01-19 10:32崔钦淑郭颜恺

浙江工业大学学报 2015年6期

崔钦淑，郭颜恺

(浙江工业大学建筑工程学院，浙江杭州 310014)

崔钦淑，郭颜恺

(浙江工业大学建筑工程学院，浙江杭州 310014)

摘要：基于钢筋混凝土Z形截面柱框架节点低周反复加载试验结果，运用有限元软件ANSYS14.5对其进行非线性模拟.针对Z形柱框架节点本身形状相对规整且内部配筋构造相对复杂的实际情况，根据配筋的实际位置，采用直接生成建模方式建模.利用不同ANSYS的弹塑性材料MKIN模型及MISO模型与不同的混凝土的本构关系Hongnestad模型、Rush模型、Sargin模型进行组合来分别模拟混凝土的材料特性，以研究不同的钢筋混凝土材料模型对模拟结果的影响.研究表明：MKIN+Sargin的组合模拟结果与试验结果吻合较好，此外不同的收敛精度控制对模拟结果也有一定的影响.

关键词：钢筋混凝土Z形柱；框架节点；ANSYS；本构关系；材料模型

Finite element analysis of quasi-static test of Z-shaped column

joints of RC frames

CUI Qinshu, GUO Yankai

(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:Based on the test results of the Z-shaped column joints of RC frames subjected to low cycle repeated loading, the nonlinear modeling is conducted with ANASYS14.5 software. Since the Z-shaped column joint of frames has a relatively regular shape but comparatively complicated internal reinforcements, the computational model is directly built according to the actual locations of steel bars. The material properties of concrete are modeled using the elasto-plastic MKIN and MISO models with the Hongnestad, Rush, and Sargin constitutive relationships provided by ANASYS to study the effect of different models of RC on the numerical results. It is shown that the numerical results given by the elasto-plastic MKIN model with the Sargin constitutive relationship are in good agreement with the test results. In addition, the control of accuracy and convergence has a certain influence on the numerical results.

Key words:RC Z-shaped column; frame joint; ANSYS; constitutive relationship; material model

随着计算机技术的迅速发展，利用计算机有限元计算模拟逐渐成为科研的一种有效手段，而且可以有效节约试验材料用量.ANSYS是目前应用较为广泛的有限元模拟软件，在建筑工程领域也有较为广泛的应用.然而钢筋混凝土结构，由于混凝土材料的特殊性，使其力学性能较为复杂，给现实有限元模拟研究也带来了极大的困难性，往往混凝土材料的准确模拟决定了其结果的准确性.国内、外有较多研究者做过相关方面的有限元模拟[1-4]，但并未系统的研究不同的混凝土本构与材料模型组合对试验结果的影响，而且对于异形柱框架节点结构本身钢筋配置的复杂性，选择合理的建模方式与混凝土本构模型，也就决定了其研究结果的可靠性与准确性.

笔者针对不同的ANSYS弹塑性材料模型及不同的混凝土本构关系的组合对混凝土材料特性进行一定的模拟，根据不同模拟结果与试验结果进行对比，找出与试验结果最为吻合的模拟模型，并通过骨架曲线，有限元应力云图等验证模拟的准确性、可靠性.可为相关钢筋混凝土异形柱节点试件的ANSYS模拟参数设置提供参考.

1试验概况

1.1试件设计

取文献[5]中的节点2(JD2)为研究对象，JD2的肢高肢厚比为3∶1，翼缘高厚比为2∶1.混凝土强度等级为C30(fc=17.19 MPa，Ec=2.85×104MPa)，梁、柱箍筋为HPB235，纵筋为HRB400，混凝土的立方体抗压强度及钢筋的材料性能按GB/T 50152—2012《混凝土结构试验方法标准》[6]实测.根据试验目的要求，将试验试件尺寸按照相似理论，将其进行1/2的比例进行缩小.缩小后柱截面尺寸肢高300 mm，肢厚100 mm，翼缘高200 mm，翼缘厚100 mm，梁截面尺寸为100 mm×275 mm.钢筋的材料试验结果均值，如表1所示.

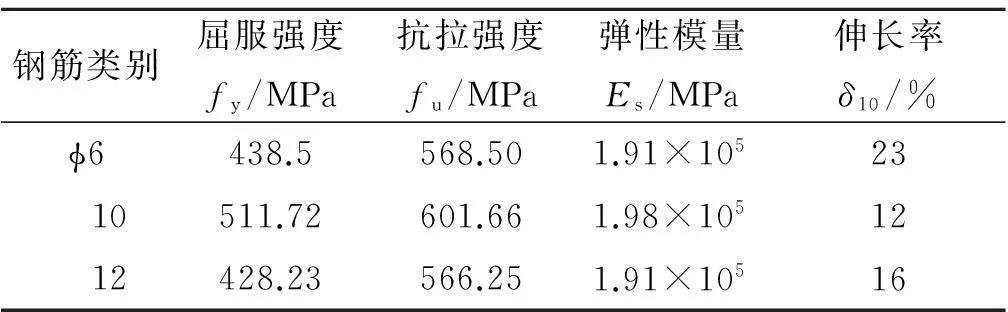
表1　钢筋材料试验结果均值

1.2加载装置及加载制度

试验利用电液伺服加载试验机进行低周往复加载，来模拟地震作用对Z形柱框架节点试件抗震性能的影响，即采用拟静力试验方法.根据(JGJ 101—1996)《建筑抗震试验方法规程》[7]，采用荷载—位移双控制的加载制度.首先利用千斤顶在柱底端施加恒定轴压力，使其达到所需的轴压比，然后再在梁端加载点利用拉压作动器同步施加反复竖向荷载，以梁端一根纵向钢筋达到屈服应变时的梁端位移，作为屈服位移.在试件屈服前的弹性阶段，采用荷载控制加载，但当试件屈服后，由于梁端塑性铰的形成，力与变形之间不再是协调的线性关系，故改用位移控制加载，并且一直加载到荷载下降为峰值荷载的85%，即Pu=0.85Pmax，此时认为试件已破坏，对应的位移即为极限位移Δu.试件的试验滞回曲线，如图1所示.

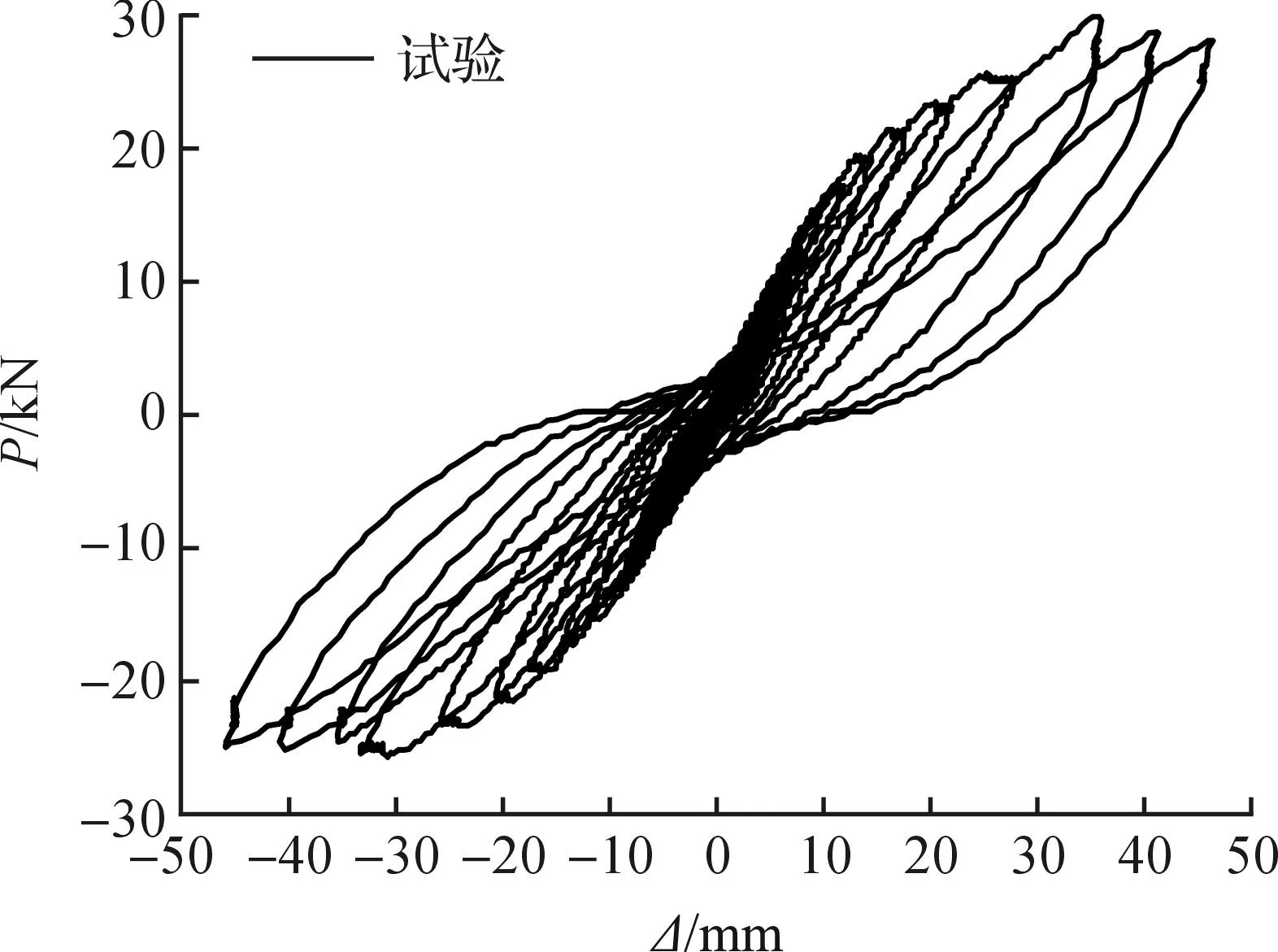
图1　试验实测滞回曲线图Fig.1　Experimental hysteresis curve

2有限元模拟

2.1模型建模方式

对于要模拟的RC Z形柱框架节点试件，ANSYS可以用两种方法来生成模型：实体建模和直接建模.

对于实体建模，则需要首先确定模型的几何边界，利用ANSYS的命令将Z形柱部分，框架节点两端梁部分分别建出，利用布尔运算进行组合，然后利用切分操作(实际切而不分)切分出不同钢筋的具体位置，设置不同部分钢筋的相应材料属性，并对钢筋单元的大小及形状进行控制，进行钢筋的网格划分，最后设置混凝土的网格尺寸大小划分网格.

对于直接建模，根据模型的形状尺寸，事先编号所需建立模型的诸多节点，并对其进行相应规律性编号，然后将相应的节点进行E(单元生成命令)指令，生成所需的钢筋单元与混凝土单元.

对于庞大或复杂的模型，尤其是对三维实体模型，实体建模更为合适，相对数据处理会少一些，但在模型生成时会需要大量CPU处理时间，而且在处理网格划分可能出现失败.对于中小型、简单的模型，直接生成较为方便，操作者对几何形状及每个单元与节点都有完全的把控.

对于要模拟的Z形柱框架节点，采用直接生成建模方式，因为对于该试件，规模相对较小，但需要分析内部钢筋等细部受力情况，如果采用实体建模，需要切分出所有纵筋以及箍筋的位置，而且网格划分也易出错，与直接建模相比占用大量CPU处理时间，故采用直接生成建模方式，相对准确而不易出错.

2.2Z形柱节点ANSYS计算模型

根据上述试验试件尺寸，建立与上述试件尺寸、配筋等完全一致的ANSYS有限元模型.采用直接生成方式建模，混凝土采用钢筋混凝土工程中最常用的solid 65单元，该单元为3D加筋实体单元，用于模拟无筋或加筋的3D实体单元，具有受拉开裂和受压破碎的性能，其梁单元尺寸为10 mm×10 mm×80 mm，柱单元尺寸为20 mm×20 mm×40 mm，节点加密区单元尺寸为20 mm×20 mm×10 mm；钢筋采用link180单元，该三维杆单元在杆轴的方向为拉压单元，单元的每个节点有三个自由度：沿着节点坐标系X，Y，Z三个方向的平动位移，具有塑性、蠕变、旋转、大变形和大应变等功能.建模所用数据严格按照试验数据采用，有限元模型如图2所示.

模型建立后在模型柱上端约束截面的两个水平方向自由度，即UX，UY自由度，UZ方向施加柱端压力，使其达到相应试验所需的轴压比，柱底端截面施加三个方向的约束，即约束UX，UY，UZ(自由度，将左、右梁加载点截面的所有节点进行UZ方向的耦合，将耦合点作为试验时的加载点，然后按实际试验加载时的梁端位移变化在梁两端进行低周往复加载.为了使模拟结果能较好收敛，加载过程始终采用位移加载控制，且每一荷载步加载位移大小严格按照该试件试验过程中每一荷载步的位移大小进行相应的加载，而且位移控制加载较力控制加载能更好的帮助收敛且模拟出下降段[8].

2.3材料屈服准则与破坏准则

混凝土常用的本构关系[9]有美国学者提出的Hongnestad模型，其表达式为

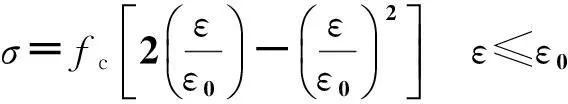
(1)

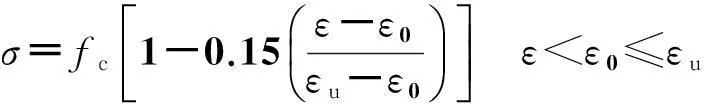
(2)

德国Rush建议的模型，下降段用水平段代替：

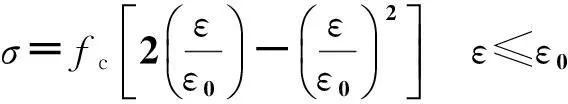
(3)

水平段σ=fcε<ε0≤εu

(4)

1964年Saenz提出一个关于σ-ε曲线的公式，之后Sargin对该公式进行改进，即

(5)

式中：A=E0/Es，E0为混凝土初始弹性模量，Es=σ0/ε0为应力峰值时的割线模量；k3=σ0/ε0为侧限对强度的影响系数，取k3=1时，适合于无侧向约束的素混凝土；D为主要影响下降段的参数，D越小，其下降段越为明显.

混凝土破坏准则采用五参数Willam-Warnke准则，其中张开裂缝传递系数取0.5，闭合裂缝传递系数取0.95，为得到较准确的计算结果关闭压碎功能.为使计算更易收敛，选择solid65单元的KEYPOT选项，令KEYPOT(1)=1，即不考虑形函数的附加项；令KEYPOT(7)=1，即考虑开裂后的拉应力释放系数，慢慢释放拉应力以帮助收敛[8].ANSYS中常用的弹塑性材料模型有双线性随动强化模型BKIN，多线性随动强化模型MKIN与KINH，双线性等向强化模型BISO、多线性等向强化模型MISO.在ANSYS14.5中，MISO模型如果定义混凝土下降段，则会提示错误，故将MISO与Rush模型相结合，组合形式如表2所示.

钢筋采用理想的弹塑性模型(双线性随动强化模型BKIN)，如图3所示.

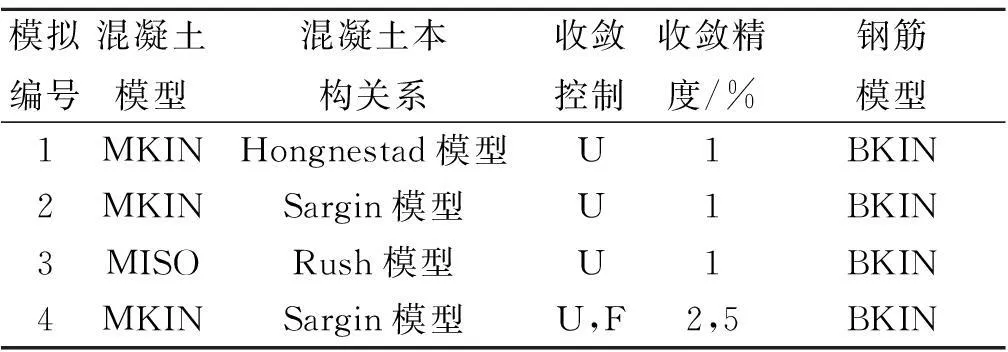
表2　分析模型表

模拟结果显示：在用MISO+Rush模拟时试件并未达到荷载极限位移值便已发生破坏，且极限荷载值也小于试验极限荷载值，而对于其它三种模拟情况，其极限位移与试验模拟大致相符，其模拟极限荷载都不同程度大于试验极限荷载，究其原因是因未充分考虑钢筋混凝土之间的滑移，以及软件默认混凝土为理想弹塑性材料所致.

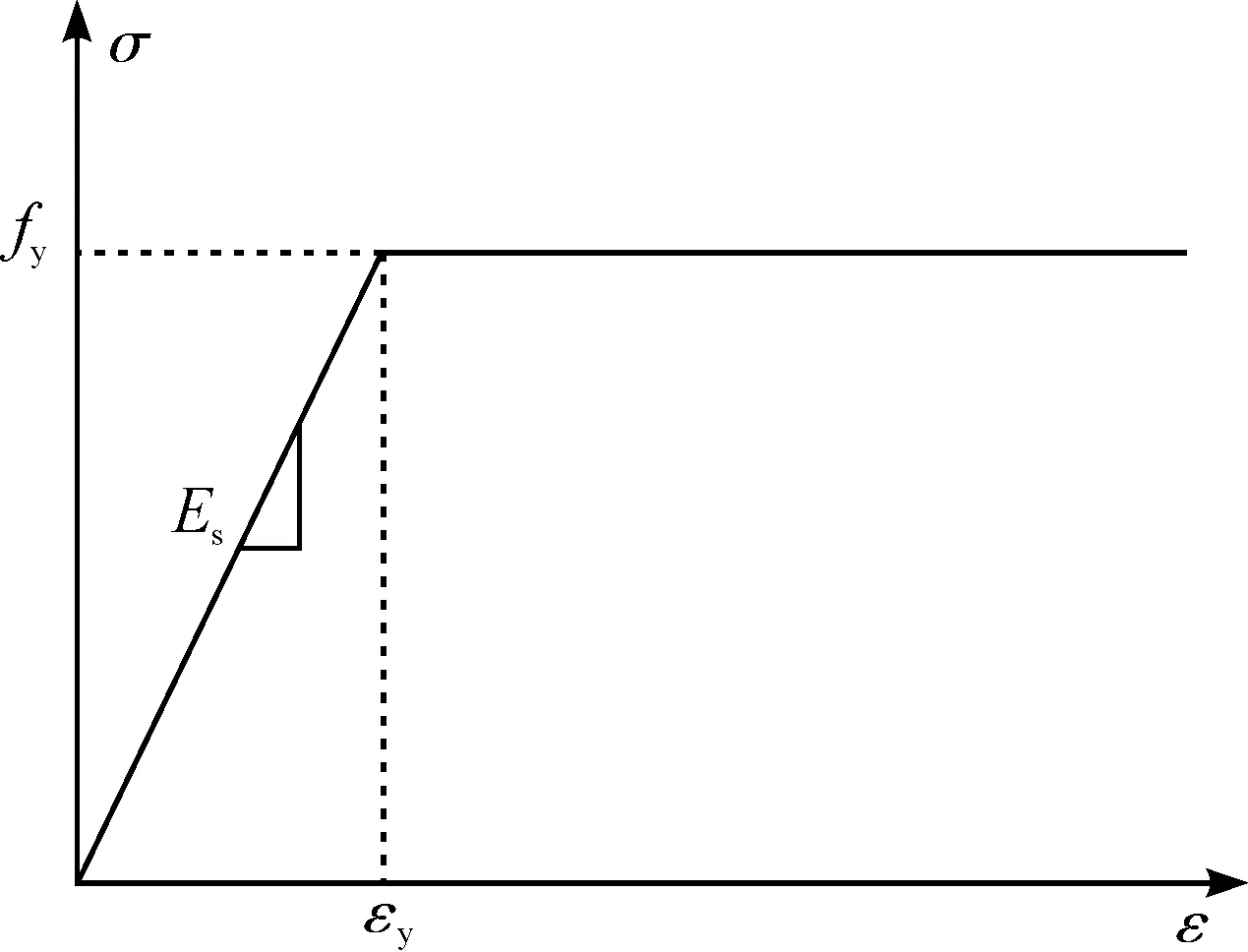
图3　钢筋的本构模型Fig.3　Constitutive model of steel bar

2.4有限元结果分析

根据试验与有限元模拟结果绘制相应的骨架曲线，如图4所示.模拟编号4与试验骨架曲线对比，如图5所示.

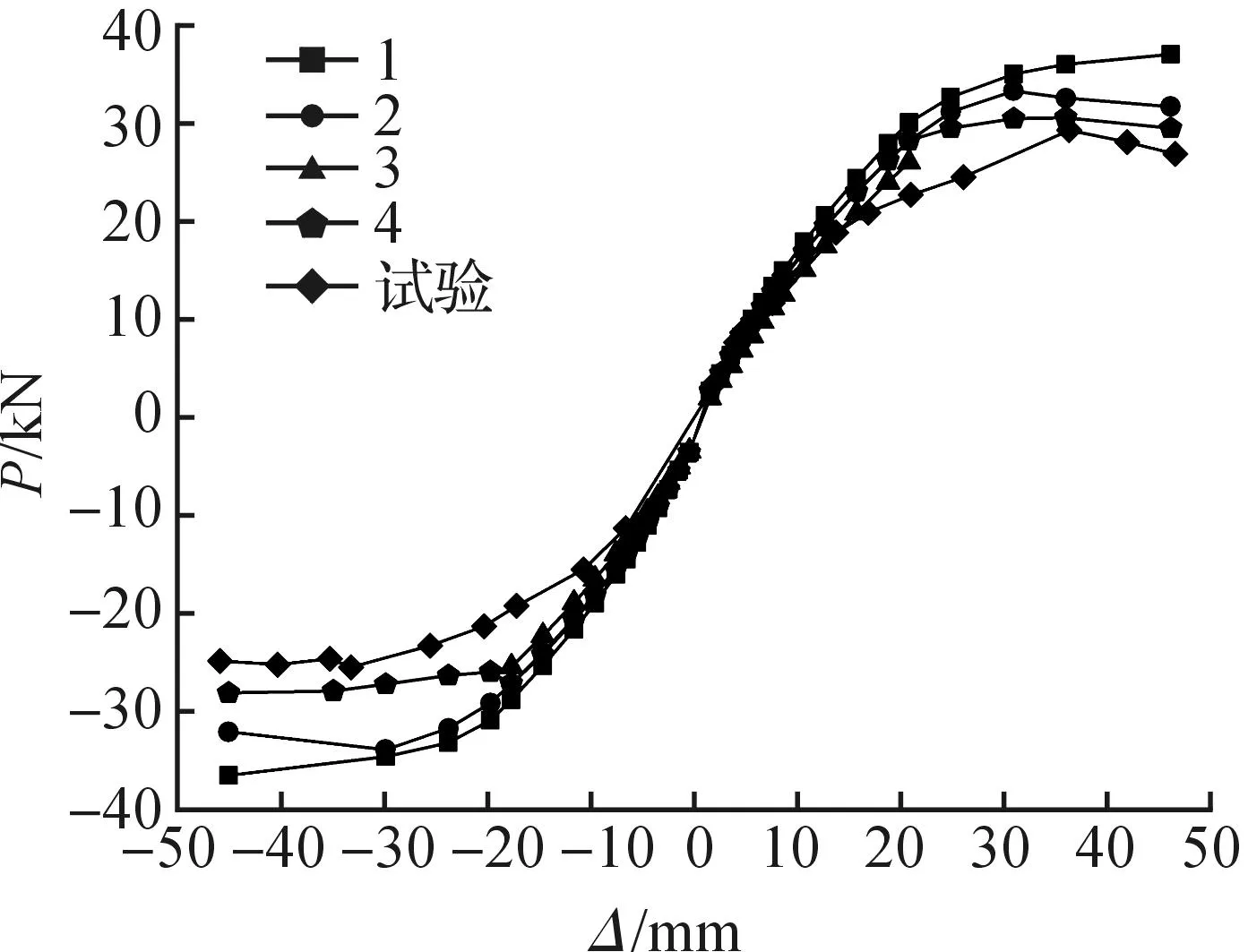
图4　骨架曲线对比分析图Fig.4　Comparative analysis of skeleton curves

图5　模拟4与试验骨架曲线对比图Fig.5　Comparison of simulation and test of skeleton curves

从图4可看出：模拟编号1，2，4的骨架曲线与试验骨架曲线的变化趋势大体一致.由图5可知模拟编号4与试验结果吻合较好.由于模拟时完全按照试验加载的位移进行加载控制，故对于模拟结果的准确性，利用梁端屈服荷载值与梁端极限荷载值两项进行比较，其中对于屈服荷载值，通过对骨架曲线采用能量等值法[5]求得其屈服点，从而确定其屈服荷载，对比如表3所示.

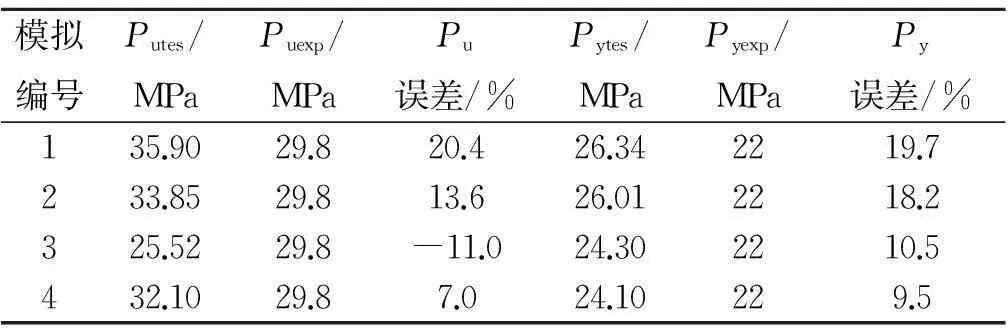
表3　ANSYS模拟与试验实测极限荷载值、屈服荷载值对比1)

注：1)Putes，Puexp，Pytes，Pyexp，分别为有限元模拟极限荷载值、试验极限荷载值、有限元模拟屈服荷载值及试验屈服荷载值.

针对误差相对较小的模拟编号4与试验结果做进一步的对比，绘制其结构变形图如图6所示，钢筋应力图，如图7，8所示.

图6　结构变形图Fig.6　Deformation of the structure

图7　纵筋应力云图Fig.7　Stress cloud of longitudinal reinforcement

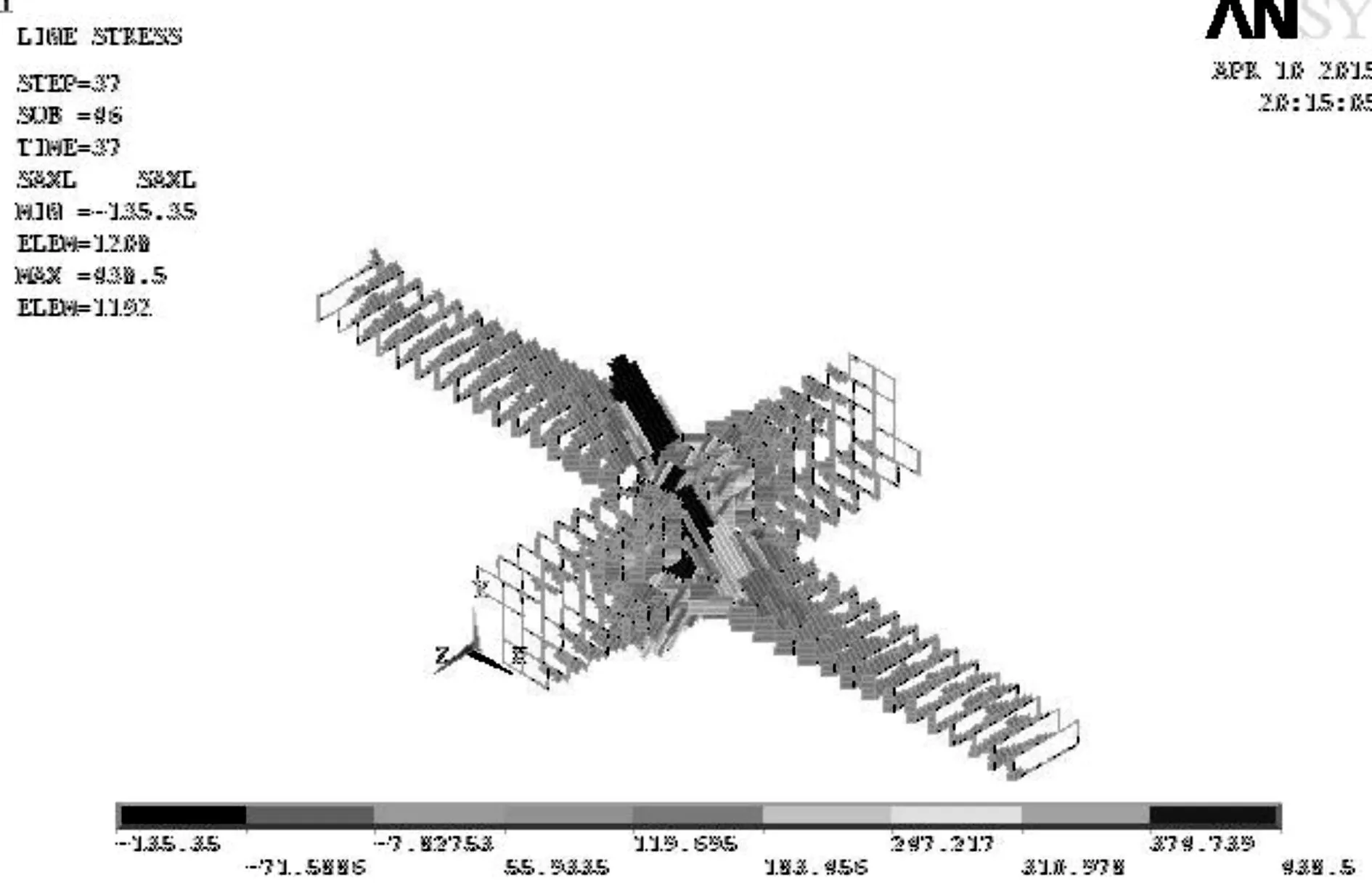
图8　箍筋应力云图Fig.8　Stress cloud of stirrup

从图7，8中可以看出：其箍筋与纵筋的应力在加载到最后荷载步时，其梁纵筋在节点附近的强度达到了最大值522.79 MPa，根据实测表1中纵筋抗拉强度约为566.25 MPa，屈服强度约为428.23 MPa，从云图可看出在梁与翼缘相交处钢筋达到屈服，而节点附近箍筋模拟其最大强度为438.5 MPa，从箍筋云图中也可看出节点中翼缘处的箍筋达到屈服强度438.5 MPa，而腹板中的箍筋没有屈服，与试验测试结果大致相符.

由于混凝土选用的多线性随动强化MKIN模型，此模型适用于Mises屈服准则，故绘制von Mises应力.从图9中可观察到：节点核心区翼缘混凝土达到了试验测得的混凝土轴心抗压强度，而从图10中可以看出：最终裂缝在节点核心区扩展，试验中试件的节点核心区翼缘混凝土保护层剥落，节点翼缘箍筋屈服后，承载力快速降低，也可验证有限元模拟的准确性.

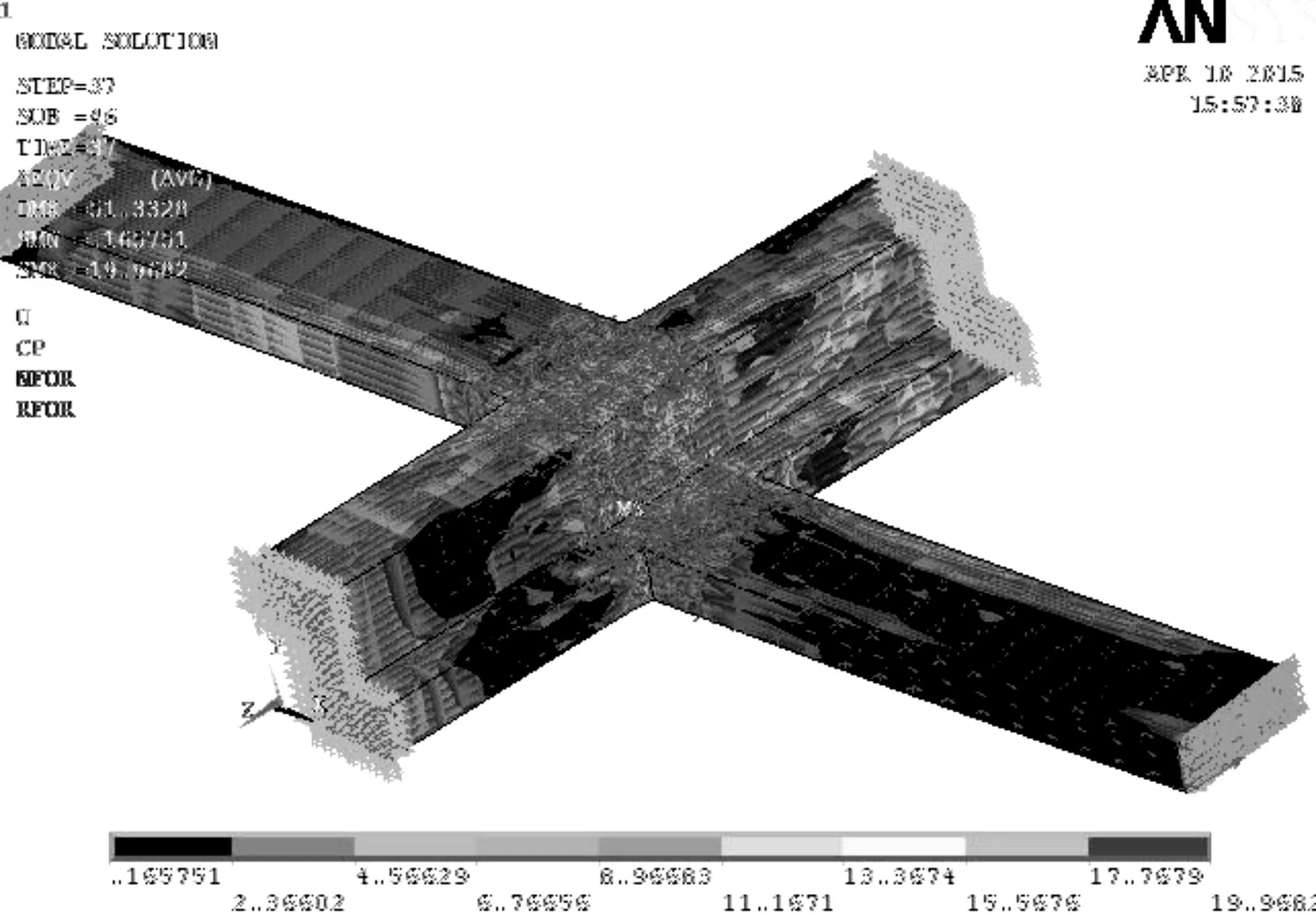
图9　Von Mises应力Fig.9　Von Mises stress

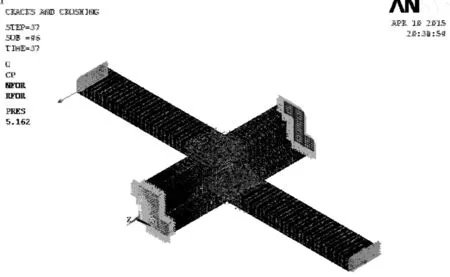
图10　节点裂缝图Fig.10　Crack graph of the joint

3结论

对于钢筋混凝土Z形柱框架节点拟静力试验有限元模拟，利用直接生成建模的方式较为方便、准确，其建模过程也相对简单，模型生成较为容易.使用多线性随动强化模型MKIN来模拟Z形柱框架节点的混凝土材料，并且利用Sargin的混凝土本构关系来定义Z形柱框架节点混凝土的应力-应变曲线，其对Z形柱框架节点的模拟结果吻合较好.对于收敛准则的控制，采用位移与力同时控制的收敛准则，可以较为准确模拟出Z形柱框架节点试件真实的试验过程，研究结果可为混凝土异形柱框架节点结构分析提供参考.

参考文献：

[1]洪健.基于ANSYS的混凝土框架非线性分析[D].广州：中山大学，2009.

[2]赵滇生，张蕾春，杨德桔，等.不等肢L形截面型钢钢筋混凝土异形柱极限承载力的试验研究[J].浙江工业大学学报，2010，38(6)：638-642.

[3]OKAMURA H, MAEKAWA K. Nonlinear analysis and constitutive methods of reinforced concrete [M]. Tokyo：University of Tokyo，1991.

[4]苏友文，马倩雯，李超飞，等.二次受力下预应力碳纤维布加固混凝土梁抗弯性能研究及数值分析[J].浙江工业大学学报，2014，42(4):378-387.

[5]崔钦淑，杨俊杰，康谷贻.钢筋混凝土Z形截面柱框架节点抗震性能试验研究[J].建筑结构学报，2012，33(6)：86-95 .

[6]中华人民共和国住房和城乡建设部.GB/ T 50152—2012混凝土结构试验方法标准[S].北京：中国建筑工业出版社，2012.

[7]中国建筑科学研究院.JGJ 101—1996建筑抗震试验方法规程[S].北京：中国建筑工业出版社，1997.

[8]江见鲸，陆新征. 混凝土结构有限元分析[M]. 北京：清华大学出版社，2005.

[9]王新敏. ANSYS工程结构数值分析[M]. 北京：人民交通出版社，2007.

(责任编辑：陈石平)

文章编号：1006-4303(2015)06-0690-05