GTN损伤模型的算法研究及试验验证

王效贵,李晓叶

(浙江工业大学 机械工程学院，浙江 杭州 310014)

GTN损伤模型的算法研究及试验验证

王效贵,李晓叶

(浙江工业大学 机械工程学院，浙江 杭州 310014)

摘要：基于GTN细观损伤本构理论，引入了塑性极限载荷模型，将完全隐式积分算法与隐式有限元计算相结合，建立了相应的数值积分算法.通过编写用户自定义材料子程序(UMAT)，实现了修正的GTN模型在有限元软件ABAQUS中的应用.通过缺口圆棒试样损伤与断裂的数值模拟，对修正的GTN模型进行了验证，并分析了缺口圆棒试样的裂纹萌生点位置，裂纹扩展情况及应力三轴度的变化.数值预测与试验结果吻合较好，表明修正的GTN模型可以有效的描述材料的损伤和断裂现象.

关键词：GTN模型；数值算法；损伤断裂；有限元法

Algorithm study and experiment validation of GTN damage model

WANG Xiaogui, LI Xiaoye

(College of Mechanical Engineering, Zhejiang University of Technology, Hangzhou 310014, China)

Abstract:The corresponding numerical integral algorithm is established by adding the plastic limit load model into the GTN mesoscopic damage constitutive model and combining the fully implicit integration algorithm and the implicit finite element. It is implemented in the finite element software ABAQUS by using the user material subroutine (UMAT). The modified GTN model is verified by simulating the damage and fracture of notched round bar. The crack initiation site and propagation path, and the change of stress triaxiality were analyzed. The numerical predications are in good agreement with the experimental observations. It also shows that the modified GTN mesoscopic damage model can effectively reveal the damage behavior and predict the fracture of the material.

Key words:GTN model; numerical algorithm; damage and failure; finite element method

损伤和断裂是工程材料的常见失效模式.材料中的夹杂物或二相粒子与基体的脱粘或自身开裂，将会引起孔洞的形核、长大及聚合，最终形成一定尺度的宏观裂纹，这是导致材料失效的根本原因.近年来，很多学者采用不同方法对损伤断裂问题展开研究.刘俊新[1]等采用三维重建技术研究了泥页岩盖层在载荷作用下的裂纹扩展与演化规律；蔡增伸[2]等通过力控制法对金刚石膜的断裂韧性进行了研究.苏彬[3]等自行设计实验装置研究了循环载荷作用下的微动疲劳特性和裂纹位置.

目前应用最为广泛的损伤模型是GTN模型，它是一种以孔洞体积分数为损伤变量反映材料内部微小缺陷的损伤模型，基于这一模型国内外学者取得了诸多研究成果.Vadillo[4]等通过数值算法研究了GT模型中的损伤参数q1和q2，发现这两个参数并不是常数，而是与应力三轴度和初始孔隙率相关的变量；邢佶慧[5]等通过数值模拟的方法，分析了初始孔洞体积分数，孔洞形核体积分数及材料失效时的孔洞破坏体积分数对断裂失效的影响.由于原Gurson模型没有考虑不连续孔洞的影响，不能预测孔洞之间的颈缩现象.因此，笔者基于GTN细观损伤理论，引入塑性极限载荷模型，采用Ramberg-Osgood硬化准则，从数值积分算法着手，模拟高导无氧铜(OFHC)材料的损伤演化和断裂失效过程，并与试验作对比，验证其可行性.

1GTN模型的算法研究及数值实现

GTN模型的屈服函数[6]表示为

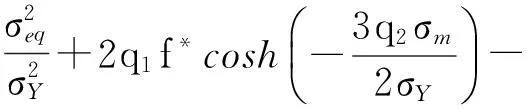
1-(q1f*)2

(1)

式中：σeq为宏观Mises等效应力；σm为宏观静水应力；σY为流动应力；q1和q2为损伤参数；f*为孔洞体积分数函数，定义为

(2)

式中：f为孔洞体积分数；fc为开始聚合时的临界孔洞体积分数；ff为材料断裂时的临界孔洞体积分数.

由于原Gurson模型不能预测孔洞之间的颈缩现象，因此在GTN模型中引入塑性极限载荷模型来描述这一现象.该模型给出的轴对称球形孔洞聚合公式[7-8]为

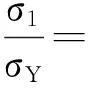
(3)

式中：Rr为球形孔洞的当前半径；L为单胞的当前长度；σ1为最大主应力.

OFHC在塑性屈服后，表现出轻微的硬化现象，为了反映这个现象，采用Ramberg-Osgood硬化准则，其曲线关系为

(4)

式中：σ0为初始屈服应力；ε0为初始屈服应变；k为硬化系数；ρ为硬化指数.

根据Aravas[9]提出的向后Euler完全隐式积分算法，更新应力应变关系.n表示增量步，为方便书写，省略下标n+1.假设给定的应变增量全为弹性应变增量，计算弹性试应力

σtrial=σn+C：Δε

(5)

式中：C为四阶弹性模量；Δε为总的应变增量.

根据关联流动准则，更新n+1增量步时的宏观塑性应变增量为

(6)

(7)

根据Hook定律，结合式(5，6)，得到n+1增量步时的宏观柯西应力为

σ=σtrial-KΔDmI-2GΔDeqN

(8)

式中：G为剪切模量；K为体积模量.将式(8)分别映射到I和N方向，得到当前时刻的宏观静水应力和宏观等效应力为

(9)

因此，宏观柯西应力又可表示为

(10)

Δf=(1-f)ΔDm+

(11)

(12)

将式(4，9，11，12)代入式(1)，得到n+1增量步时的屈服函数为

F(ΔDeq,ΔDm)=0

(13)

(14)

根据式(7，13，14)推导一致切线刚度矩阵T，得到

(15)

式中：Mijkl的表达式见文献[9]，Jijkl=(δikδjl+δilδjk)/2.

根据以上推导的离散公式，下面给出修正的GTN模型在用户子程序(UMAT)中的实现流程图，如图1所示.

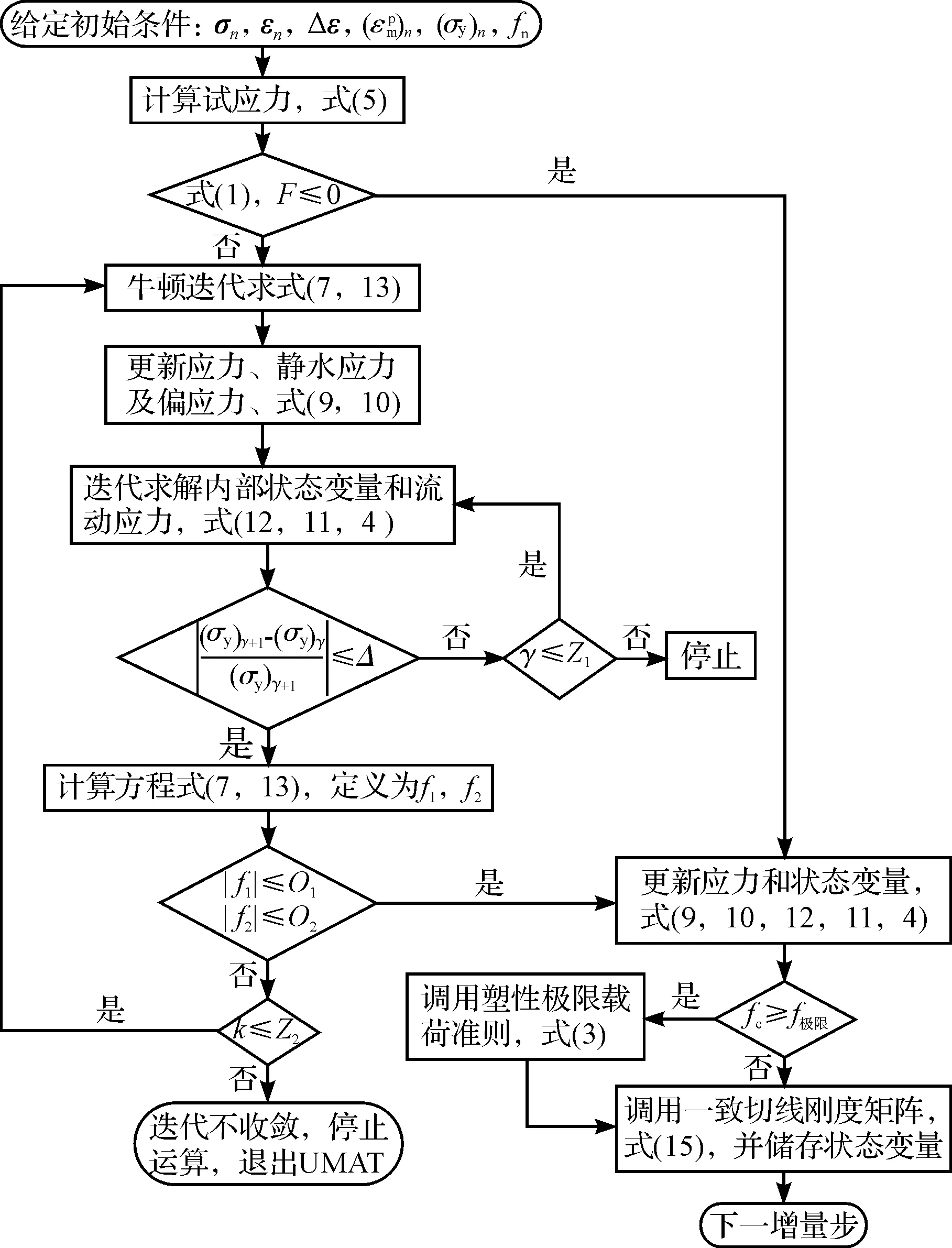
图1　流程图Fig.1　Flow chart

2单轴拉伸试验

缺口圆棒试样的单轴拉伸试验是研究韧性金属材料损伤断裂的最好方法，因此，采用如图2所示的高导无氧铜光滑和缺口圆棒试样，进行单轴拉伸试验.光滑试样标距段的直径为10mm.缺口试样有三个重要几何参数，分别为缺口宽度d、缺口半径r和净断面直径D，实测数据如表1所示.采用RG4100微机控制电子万能试验机，在室温状态下完成单轴拉伸试验.试验采用位移控制，引伸计的标距为20mm.光滑试样的位移加载速率为0.3mm/min.基于不同缺口尺寸，试样φ6r1，φ6r2，φ8r1，φ8r2的位移加载速率分别为0.05，0.08，0.10，0.15mm/min.试验完毕后，测量缺口部位的d和D，结果列于表1.由表1中的断面收缩率可以看出：净断面直径越大，断面收缩率越大；同一种净断面直径，缺口半径越大，断裂收缩率越大.

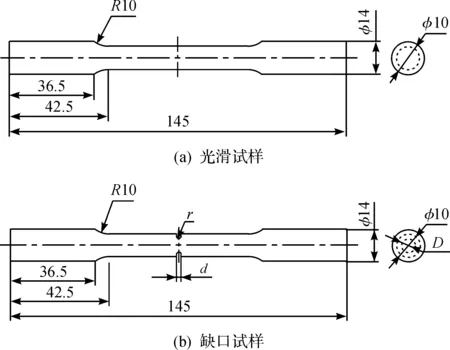
图2　单轴拉伸试样Fig.2　Uniaxial tensile specimens

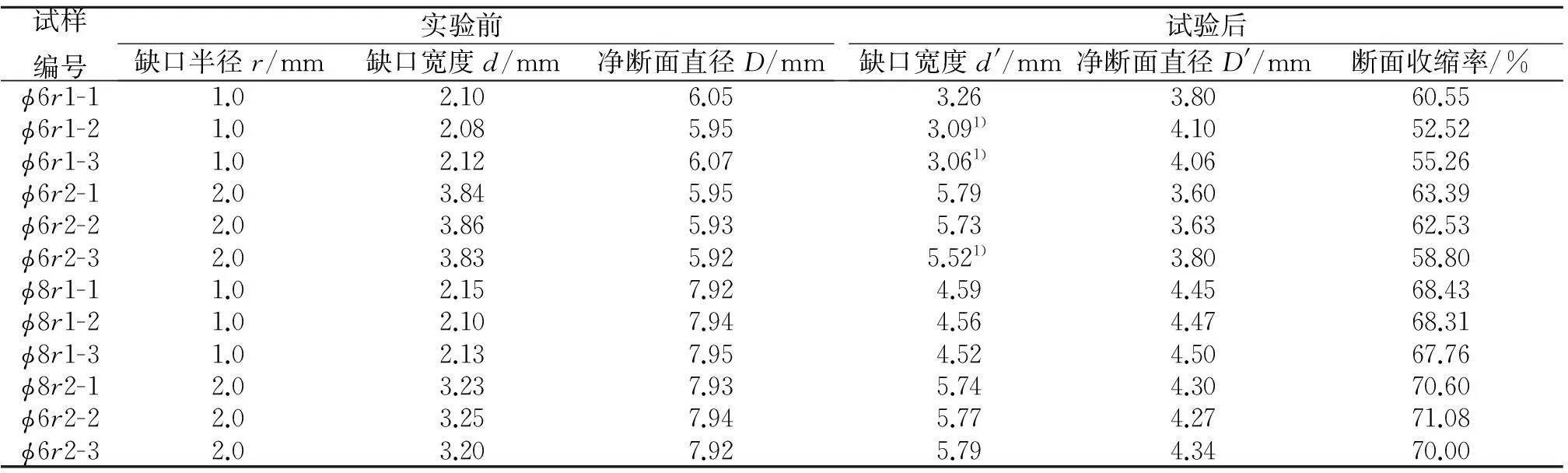
试样编号实验前缺口半径r/mm缺口宽度d/mm净断面直径D/mm试验后缺口宽度d'/mm净断面直径D'/mm断面收缩率/%ϕ6r1-11.02.106.053.263.8060.55ϕ6r1-21.02.085.953.091)4.1052.52ϕ6r1-31.02.126.073.061)4.0655.26ϕ6r2-12.03.845.955.793.6063.39ϕ6r2-22.03.865.935.733.6362.53ϕ6r2-32.03.835.925.521)3.8058.80ϕ8r1-11.02.157.924.594.4568.43ϕ8r1-21.02.107.944.564.4768.31ϕ8r1-31.02.137.954.524.5067.76ϕ8r2-12.03.237.935.744.3070.60ϕ6r2-22.03.257.945.774.2771.08ϕ6r2-32.03.207.925.794.3470.00

注：1) 为在单轴拉伸试验中材料没有拉断.

由光滑试样单轴拉伸试验得到的真实应力—应变曲线，如图3所示.由弹性阶段的斜率，得到OFHC的弹性模量为E=108 GPa.基于国标GB/T 228.1—2010，确定初始屈服应变为ε0=0.026 85，且满足σ0=Eε0，屈服极限为σy=290 MPa，强度极限为σu=314 MPa.OFHC在塑性屈服后，表现出轻微的硬化现象.采用公式(4)给出的Ramberg-Os-good硬化准则，曲线拟合后得到硬化系数为k=0.75和硬化指数为ρ=27.

图3　光滑圆棒试样的真实应力—应变曲线Fig.3　True stress-strain curves of smooth round bar specimens

由缺口试样单轴拉伸试验得到的载荷—位移曲线如图4所示.对每种缺口试样进行3次重复试验，获得的载荷—位移曲线具有很好的一致性.试验曲线分成三个阶段：第一，试验开始到载荷最大值，这一期间载荷快速增大，而材料的变形程度非常小；第二，载荷最大值到裂纹萌生点(拐点)，当达到最大载荷时孔洞开始聚合，材料承载能力逐渐减弱，同时缺口半径处出现颈缩现象，纵向变形快速增大；第三，裂纹萌生点到材料断裂失效，随着裂纹的萌生和扩展，损伤演化程度加快，载荷急剧降低，材料承载能力下降，最终导致断裂破坏.图4可以看出：缺口试样的净断面直径越小，材料的断裂失效出现的越早；同一种净断面直径，缺口半径越小，断裂破坏产生的越快；净断面直径越大，载荷—位移曲线中峰值越高.

图4　缺口试样的载荷—位移曲线Fig.4　Load-Displacement curves of notched specimens

3算例及讨论

3.1有限元模型

建四分之一轴对称有限元模型，如图5所示.边界条件的施加分为3部分：在左端面，施加轴向位移载荷，试样φ6r1，φ6r2，φ8r1，φ8r2的位移大小分别为0.6，0.75，1.5，1.5 mm；在右端面，施加y向对称位移约束；在x=0对称面上，施加x向对称位移约束.为了能够很好地模拟缺口根部区域较大的塑性应力应变梯度，将该区域的网格细化，最小网格尺寸为0.1 mm.为了提高计算速度，远离缺口区域的网格尺寸为0.2 mm.采用嵌入GTN模型的有限元软件ABAQUS，选用八节点轴对称缩减积分单元(CAX8R)，进行数值模拟断裂预测.

图5　缺口圆棒试样的有限元模型Fig.5　FEA model of notched specimens

3.2GTN模型的参数确定

由于GTN损伤模型中的体胞是假设的，因此f0的取值需根据模拟结果和试验数据对比而确定.以试样φ6r1-1为研究对象，当给定的f0能够使数值模拟结果和试验数据基本相吻合时，则认为此时的f0即为要确定的初始孔隙率，最终确定f0=0.001.文献[4]给出了损伤参数q1和q2随应力三轴度的变化图，依据给定的关系图，可以初步确定损伤参数q1和q2，由于不同材料的实际损伤情况并不一致，因此根据数值预测结果和试验数据进一步修正，最终得到q1=1.2，q2=0.8.根据本试验的实际情况，结合文献[5]中介绍的方法，最终确定fN=0.004 5，ff=0.4.

3.3结果与讨论

根据确定的损伤参数，将修正的GTN模型嵌入ABAQUS软件进行断裂预测，分析缺口圆棒试样裂纹萌生点位置和扩展情况，以及应力三轴度的变化.

3.3.1裂纹萌生点位置及扩展路线的预测

图4展示了缺口试样裂纹萌生点和裂纹扩展路线，图4中的黑点代表裂纹萌生点位置.可以清楚的看到：裂纹萌生最早产生于缺口试样的中心位置附近，随后向缺口试样的尖端方向逐渐发展，随着塑性变形的增大，裂纹快速扩展并贯通缺口根部，最终造成材料的断裂失效.这是因为，由于塑性变形的增大，孔洞体积分数也随之增加，当达到塑性极限载荷时，微孔洞开始聚合，孔洞体积分数逐渐由f变成f*，并急剧增大，当f*增加到一定程度时，缺口试样的中间部位裂纹开始萌生.随着裂纹的快速长大和扩展，载荷急剧下降，材料的承载能力降低，当f*增加到材料断裂的临界值时损伤失效产生.

从图4中的试验和数值模拟曲线看到：裂纹萌生点位置的数值预测与试验结果较为接近，裂纹扩展路线的预测结果与试验曲线趋势基本一致.表明修正的GTN模型能够模拟缺口圆棒试样的断裂失效特征，验证了该模型的有效性，该方法的合理性和可行性.

3.3.2应力三轴度的变化

应力三轴度定义为平均应力与等效应力的比值，它是影响韧性材料断裂的一个重要因素，通常根据试样最小横截面来评估.图6给出最大载荷条件下应力三轴度的变化过程，图7给出裂纹萌生点附近应力三轴度的变化过程.

以上四幅图显示，净断面直径相同，缺口半径越小，最小横截面上的应力三轴度越大；应力三轴度通常在缺口试样的中间部位最高，在自由边附近最低.由3.3.1节知道：裂纹萌生最早发生于缺口试样中心部位附近，随着塑性变形的增大，加剧了缺口试样中心位置的裂纹萌生扩展，从而导致缺口根部的孔洞体积分数快速增大.由GTN模型的屈服函数可以知道，当孔洞体积分数增大到一定程度时，平均应力远大于等效应力，因此出现了上图所述规律.比较图6,7看到：同一种缺口结构，图7中的应力三轴度要比图6中的偏大.这是因为，当达到塑性极限载荷时微孔洞刚开始聚合，裂纹萌生并没有完全开始，孔洞体积分数相对较小，此时等效应力所起的作用比平均应力大，应力三轴度较小.而在裂纹萌生点附近，由于塑性变形的增大，加剧了裂纹萌生和快速扩展，导致此时的孔洞体积分数比最大载荷工况下更大，平均应力的影响远远大于等效应力，所以应力三轴度较大.同时还可以发现，同一种缺口半径，净断面直径越小，应力三轴度越大.这是因为净断面直径越小，此处的应力集中对损伤断裂的影响更加敏感而造成.

图6　最大载荷下应力三轴度沿最小截面的变化Fig.6　Variations in stress triaxiality along minimum section corresponding to maximum load

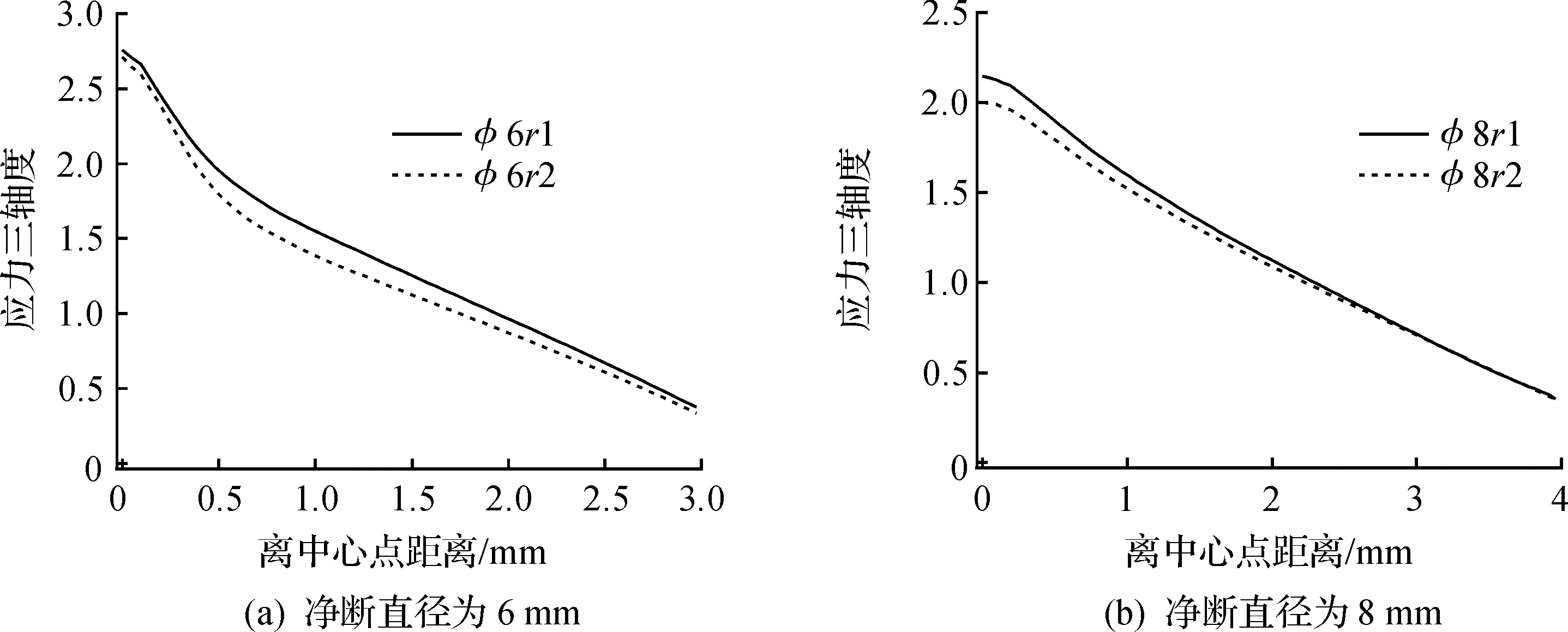
图7　裂纹萌生下应力三轴度沿最小截面的变化Fig.7　Variations in stress triaxiality along minimum section corresponding to crack initation

图4中的试验曲线显示：试样从早到晚的断裂情况依次是φ6r1，φ6r2，φ8r1，φ8r2.观察图6，7发现：应力三轴度由大到小的顺序是φ6r1，φ6r2，φ8r1，φ8r2.而应力三轴度越大，孔洞体积分数的增加就越急剧，裂纹萌生和扩展速度越快，断裂破坏产生的就越早.因此GTN模型的模拟结果和试验结果吻合良好.

4结论

采用嵌入修正的GTN模型的有限元软件ABAQUS进行断裂模拟，得出以下几点结论：1) 通过对缺口圆棒试样裂纹萌生点位置和扩展路径的分析发现，裂纹萌生首先产生于缺口试样的中部，而不是缺口试样的尖端.一旦裂纹萌生，载荷急剧下降，材料的承载能力快速降低.2) 应力三轴度的分析表明，缺口试样的中间位置应力三轴度最大，自由边附近最低.随着塑性变形的增加，孔洞体积分数急剧增大，加剧了裂纹的萌生和长大，从而导致缺口试样中间部位的塑性应变最大，应力三轴度也最大，因此断裂失效最早发生.3) 缺口试样的模拟结果与试验结果吻合较好，验证了修正的GTN模型具有预测材料断裂行为的可行性.

参考文献：

[1]刘俊新，杨春和，冒海军，等．基于CT图像处理的泥页岩裂纹扩展与演化研究[J]．浙江工业大学学报，2015，43(1)：66-72．

[2]蔡增伸，蒋政，王从贤，等．测定金刚石膜断裂强度及断裂韧性的力控制法研究[J]．浙江工业大学学报，2000，28(3)：216-219．

[3]苏彬，邢海军，赵颖娣，等．循环载荷应力比对微动疲劳特性的影响[J]．浙江工业大学学报，2011，39(4)：445-448．

[4]VADILLO G, FERNANDEZ-SAEZ J. An analysis of Gurson model with parameters dependent on triaxiality based on unitary cell[J]. European Journal of Mechanics. A: Solids，2009，28(3)：417-427．

[5]邢佶慧，史一剑，刘文涛，等．建筑钢材GTN损伤模型参数识别[J]．建筑结构学报，2014，35(4)：149-154．

[6]TVERGAARD V, NEEDLEMAN A. Analysis of the cup-cone fracture in a round tensile bar[J]．Acta Metallurgica，1984，32(1)：157-169．

[7]THOMASON P F. Ductile fracture of metals[M]．Oxford：Pergamon Press，1990．

[8]PARDOEN T, HUTCHINSON J W. An extended model for void growth and coalescence[J]．Journal of Mechanics and Physics of Solids，2000，48(12)：2467-2512．

[9]ARAVAS N. On the numerical integration of a class of pressure-dependent plasticity models[J]．International Journal for numerical methods in engineering，1987，24(7)：1397-1416．

[10]CHU C C, NEEDLEMAN A. Void nucleation effects in biaxially stretched sheets[J]．Journal of Engineering Materials and Technology，1980，102(3)：249-256．

(责任编辑：陈石平)

文章编号：1006-4303(2015)06-0660-06

中图分类号：TG146.1

文献标志码：A

作者简介：王效贵(1973—)，男，山东青州人，教授，研究方向为结构完整性，E-mail：hpcwxg@zjut.edu.cn.

基金项目：国家自然科学基金资助项目(51175469)

收稿日期：2015-05-04