基于泊松方程的图像修复与融合的研究

基于泊松方程的图像修复与融合的研究

高 丰 誉

(福建师范大学 福清分校，福建 福清 350300)

摘要：提出了采用泊松方程的图像融合算法用于实现数字图像的简单修复和无缝拼接；在图像欲修复和融合区域通过解泊松方程在梯度映射下来构建图像；利用MFC和MATLAB进行仿真，比较实际修复和融合的例子与结果，探讨了方法的实际应用效果；实验结果表明：基于泊松的图像编辑方法可以较好地实现图像的简单修复和背景颜色较为单一的彩色图像的融合。

关键词：图像融合；泊松方程；梯度场

doi:10.16055/j.issn.1672-058X.2015.0012.004

收稿日期：2015-06-01；修回日期：2015-07-10.

作者简介：高丰誉(1988-)，女，福建福清市人，助理实验师，硕士，从事图像处理研究.

中图分类号：TN911文献标志码：A

图像拼接是将两幅或两幅以上的图像通过配准和融合形成单幅宽视场图像或动态远景图。目前，图像拼接技术主要应用于虚拟现实[1]、数字视频[2]、卫星遥感[3]、医学图像分析[4]等领域。图像融合则是消除图像拼接痕迹的关键技术和重要步骤，是为了确定重叠的区域内每个像素的取值。图像融合技术要求满足色度和亮度一致、拼接痕迹不明显、无鬼影、无拼接黑边等要求。Patrick P 等[5，6]于2003年提出了基于泊松方程的图像编辑方法，在重叠区域内利用图像梯度场进行引导插值，求解区域内梯度和的最小值，并利用泊松方程进行求解。利用泊松方程应用于图像的简单修复和融合[7，8]，使用MFC和MATLAB进行仿真，发现方法在一定范围内有一定的适用效果。

1基于泊松方程的图像内插算法

1.1泊松方程

如图1所示，S代表原始的图像区域，Ω代表着图像的空缺区域，∂Ω为Ω的边界，f为Ω区域内的图像数据值，f*为S区域内的图像数据值，为了保证平滑过渡需要保证区域内有S区和Ω对应的值相同，即：

(1)

同时为了保证区域内的变化也具有平滑性，需要满足区域内梯度变化最平缓，即区域内梯度和最小，寻找在区域内的解f满足一定边界下的泊松方程：

(2)

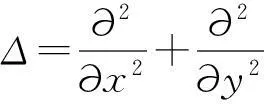
1.2图像填充

图1　相关概念

图2　指导梯度场

(3)

(4)

同样为了保证图像的平滑过渡并与目标图像有相同的轮廓，需要满足区域内融合后图像与原始图像有着最接近的梯度信息，即：

(5)

(6)

即求解方程：

(7)

1.3离散实现

对于一般的数字图像处理，函数为离散的，因此拉普拉斯求解可以用模板的方式来进行，在离散数据中选用的拉普拉斯算子为

(8)

对于函数的求解来说f是未知量，而g是已知量，为欲粘贴的图像。可以很直接地先求出g的拉普拉斯变换Δg。对于f的拉斯变换则需要分情况讨论：

(1) 假设p为Ω上的某个点，q为其对应的上下左右4个邻域的点，假定p的四邻域为Np，即：q∈Np，若Np∈Ω，则可得到：

(9)

这里Δgp为与fp对应的欲填充图像g上的点的拉普拉斯变换值。

(2) 假定Np∩∂Ω≠∅时，则式子表示为

(10)

利用式(9)、(10)便可以得到n(n为Ω内像素点的个数值)个线性方程，利用这些线性方程，就可以得到Ω内所有点的值，实现泊松方程的解。

2实验及结果分析

实验使用MFC来实现程序的编写同时利用MATLAB来实现所有的计算操作。首先调用Spalloc函数创建一个稀疏矩阵空间，并利用bicg来求解最后的泊松方程，最后使用MATLAB自带的编译器将程序编译成可执行的文件。采用文件传递的方式实现MATLAB与MFC程序间的参数传递。

2.1图像的修复

利用图像的平滑过渡可以实现简单的图像修复，图3(a)中的白色区域为图像的破损区域。进行这个修复使用的是原始图像本身，只需要在纯色图像上选取一个破损区域形状接近的图像，如图3(b)，将它作为源文件移入目标文件将破损区覆盖，如图3(c)，然后进行融合就可以实现修复。从图3(d)可以看出破损区域得到很好的平滑过渡，基本实现了修复的目的。

图3　简单图像修复

由于这里破损区域比较平滑，纹理较少，因而与纯色图像融合能够得到较好效果的修复。对于有较明显纹理的区域，如图4(a)，这时如果采用前面的修复方法，得到图4(b)的结果，可见融合后的区域与周围的区域有较为明显的差异。对于修复区域纹理比较丰富的情况，可以在其附近选取掩膜来实现对破损区域的修复，如图4(c)所示，可见得到的修复效果，如图4(d)，明显优于图4(b)。

图4　具有纹理特性的图像修复

2.2图像的黏贴融合

当目标图像与黏贴图像背景均匀且颜色相近的，如图5(a)和图5(b)，两图中天空的背景颜色基本相同，融合过程中的颜色过渡能很好的进行，使得融合后能得到较为理想的效果，如图5(b)，可以发现二者能很好地得到衔接，不会出现有任何突兀的感觉。

图5　背景颜色接近的图像黏贴

当粘贴图像与目标背景之间存在着一定的纹理差距，如图5(c)，从图5中明显可以看到：在老鹰的翅膀部位，由于背景的一致性实现了很好的融合；而在老鹰头部，由于云层的存在使的背景差异瞬时被拉大，原本有明显轮廓的云层被平滑化，使得拼接的效果大打折扣。

当粘贴图像和目标图像背景都相对均匀，但亮度差异较大，如图6(a)和图6(b)，由于图6(a)的背景相对较暗，经过融合后整个图像的亮度被极大提高，形成类似于曝光的场景，如图6(b)所示。同时粘贴图像和目标图像的背景颜色存在着较大的差异，经过融合后可以发现景物的颜色都被染上了蓝色的色调，黏贴图像的颜色出现了较大的改变。

图6　亮度和背景颜色差异较大的图像黏贴

3总结

介绍了基于泊松方程的图像修复和融合技术，它能够实现简单的图像修复和图像无缝拼接。讨论了它的适用情况和实际图像处理后的结果。若目标图像纹理较强或背景颜色与欲黏贴的图像差异较大，则得到的合成图像存在一定的拼接赝像。

参考文献：

[1] SZELISKI R.Video Mosaics for Virtual Environment[J].IEEE Computer Graphics and Applications，1996，16(2):22-30

[2] TOM R，MARK B C C.Implemen Ting Advanced Image Processing Technology in Sensor Systems for Security and Surveillance[C].Optics and Photonics for Counterterrorism and Crime Fighting III Proc of SPIE，2007

[3] LAURIE G.Automation Technology with IKONOS Satellite Imagery[C]∥Sensors Systems and Next-Generation Satellites V Proceedings of SPIE，2001

[4] LOEWKE K，CAMARILLO D W，PIYAWAT D，et al.Real-time iMage Mosaicing with a Hand-held Dual-axes Confocal Microscope[C].Progress in Biomedical Optics and Imaging Proc of SPIE，2008

[5] PEREZ P，GANGNET M，BLAKE A.Poisson image editing[J].ACM Transaction on Graphics，2003，22(3):313-318

[6] FATTAL R，LISCHINSKI D，WERMNAN M.Gradient Domain High Dynamic Range Compression[J].ACM Transaction on Graphics，2002，21(3):249-256

[7] 敬忠良，肖刚，李振华.图像融合——理论与应用[M].北京:高等教育出版社，2007

Research on Completion Fusion of an Image Based on Poisson Equation

GAO Feng-yu

(School of Electronics and Information Engineering，Fuqing Branch of

Fujian Normal University，Fujian Fuqing 350300，China)

Abstract：This paper proposes Poisson equation based image fusion algorithm for the implementation of uncomplicated completion and seamless splicing of digital image. This method constructs image reconstructed from the gradient map via the solving Poisson equation in the field of images needing to be completed and fused and uses MFC and MATLAB to process the simulation. This paper compares the examples and results of practical completion and fusion and discusses the real application effect. Experiment result shows that the image editing method based on Poisson equation can relatively better implement the uncomplicated completion of the image and the fusion between single background color images.

Key words： image fusion; Poisson equation; gradient field