遗传算法优化模糊PI的网侧变流器的控制

张 蕾，刘小河

（北京信息科技大学 自动化学院，北京 100192）

随着近几十年风力发电技术的快速发展，相对传统的恒速恒频发电技术已经逐渐被对风能利用更高效的变速恒频风力发电技术所替代。在变速恒频风力发电系统中，双馈电机已经成为主流机型，而在双馈风力发电系统中，网侧变流器的主要功能是实现网侧输入功率因数和保持直流环节稳定，从而保证机侧变流器甚至于整个双馈系统的可靠工作[1]。因此，对于网侧变流器的控制十分关键。

目前，传统的DFIG网侧PWM变流器的控制器都采用经典的比例积分（PI）控制，但PI控制抗扰动性能有些不足，尤其在电网波动的情况下，其系统的动态性能和鲁棒性有些缺陷。近年来，也有很多新的控制方法被陆续提出[2]。文献[3-4]先将正负序电流分离后接着进行双闭环PI控制；文献[5-6]基于变结构的滑模控制理论提出了新的控制方法，系统的鲁棒性得到很大提高，但滑模控制产生抖振现象也是一个重要的不稳定因素；文献[7]利用定频模型预测控制的方法实现对参考电流的准确跟踪。

本文在基于传统方法的基础上，提出基于遗传算法优化的模糊PI控制方法，来提高系统的动态性能，其基本思想为，对模糊控制器的隶属度函数用遗传算法进行寻优，将优化后的模糊PI控制器应用到电压外环和电流内环，同时利用负载电流的前馈补偿，提高系统的抗干扰能力。

1 DFIG网侧PWM变流器模糊控制器的设计

1.1 网侧变流器模糊控制器的设计

1）电流内环控制器设计

由于d轴与q轴电流的对称性，因此以d轴为例设计控制器。整流器用代替，考虑到典型Ⅰ型系统抗干扰能力较差以及电动势扰动对输出的影响，所以这里采用了抗干扰性能强的典型Ⅱ型系统设计。Ts为内环电流采样周期，KPWM为等效增益系数，L为电网进线电感，R为电网进线电阻，τi=L/R。电流内环控制框图如图1所示。

图1 d轴电流结构Fig.1 Diagram of d-axis current structure

可推出电流内环开环传递函数为

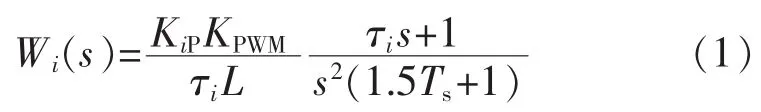
可得

由上式得到比例和积分增益

2）电压外环控制器设计

为了便于对电压外环的分析，可以把电流内环按典型I型系统等效为

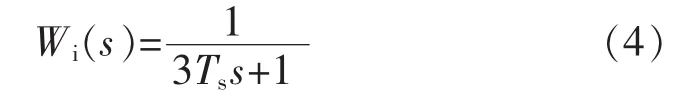
查阅文献[8]可知直流侧的电流Idc和交流电流的有效值Im之间的关系为

电压外环控制结构如图2所示。

图2 电压外环结构Fig.2 Voltage outer structure diagram

τu为电压采样时间常数；Tu为比例调节系数；Ku为积分增益。τu和 Ts合并等效为 Teu=τu+3Ts，可得电压外环开环传递函数为

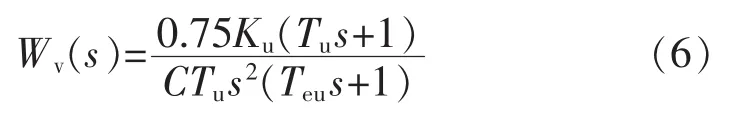
根据典型Ⅱ型系统的参数关系，令Tu=hTcm得：

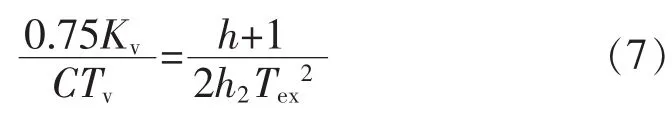
一般工程上h=5，可得PI调节参数为

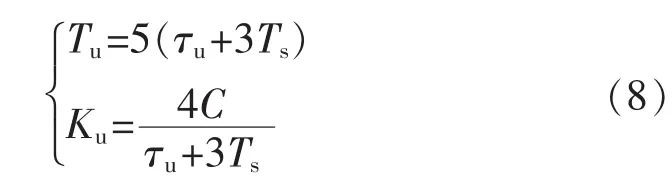
在实际调试过程中需要对参数适当修改，以达到要求。

1.2 模糊控制器的设计

传统双闭环控制系统中PI参数是恒定的，但在实际风力发电系统中，系统模型会随着条件变化而变化，PI参数如果保持不变，系统动态性能就会变差，模糊控制对数学模型要求不高，鲁棒性较好。因此将模糊控制器引入网侧变流器的电流内环和电压外环，与PI控制器结合。偏差比较大时，先用模糊控制的方法，使系统较快稳定；偏差比较小时，利用PI控制消除稳态误差。控制框图如图3所示。

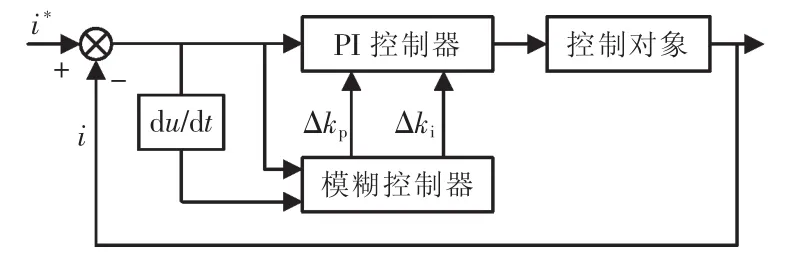
图3 模糊PI控制Fig.3 Fuzzy PI control block

以电流的dq分量为例，采用双输入双输出系统，输入量为电流的偏差e和电流的偏差变化率Δe，输出为 PI参数的变化量 Δkp、Δki。 则 PI控制器输出参数为

kp′、ki′为预整定值。

本文模糊论域采取7个，中间5个子集采用三角形隶属度函数，最左NB选取了Z型函数，最右PB选取了S型隶属度函数，采取实数编码的方式进行编码。示意图如图4所示。

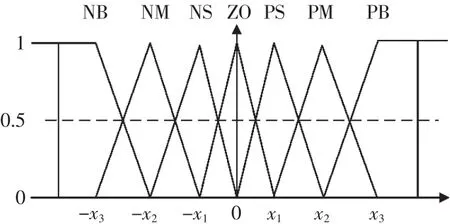
图4 模糊划分示意Fig.4 Fuzzy partition schematic

根据实验以及专家经验指定的模糊规则表1所示。

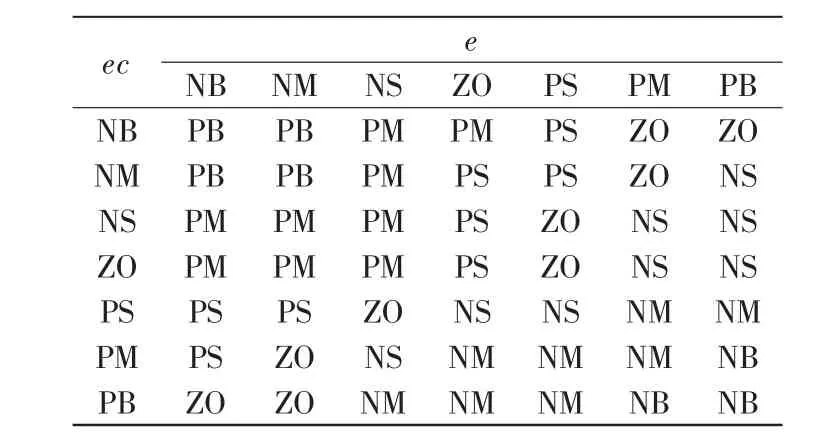
表1 Kp的模糊规则表Tab.1 Fuzzy rule table of Kp

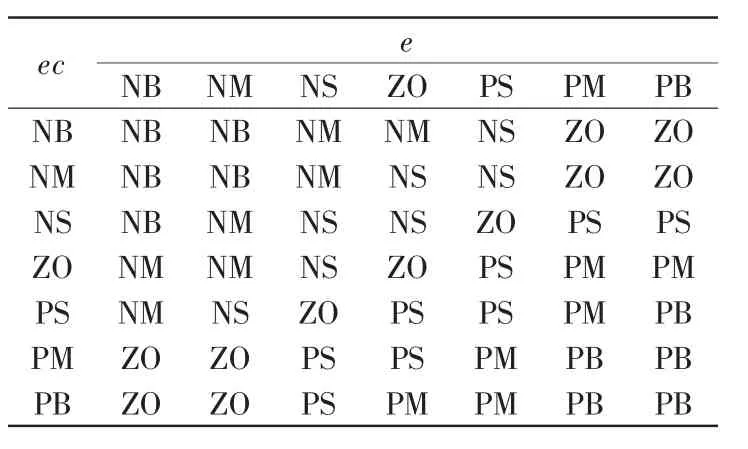
表2 Ki的模糊规则表Tab.2 Fuzzy rule table of Ki

2 基于遗传算法优化的模糊PI控制器的设计

2.1 遗传算法对模糊PI控制器的优化

遗传算法对于模糊控制器一般都是针对其数据或规则库来进行的，通常是把系统的某些重要的性能指标作为标准，通过一系列遗传搜索得到最优的隶属度函数、模糊控制规则、量化因子等。这里是对隶属度函数进行了优化[9]。

2.2 遗传算法优化过程设计

1）隶属函数的编码

一般情况下，对隶属度函数论域的划分是均匀的，但是在实际控制中对模糊论域的划分采用不均匀划分的方法，更可以满足系统在不同阶段的要求。

模糊子集顶点的横坐标值，左右2个端点到顶点的距离决定了隶属度函数的形状。为了减少参数数量，选取了左右对称的隶属度函数，要优化的参数是底边端点间的距离。

2）适应度函数函数的选择

系统的控制设计必须满足系统的性能指标，因此可以将性能指标作为适应度函数。这里的约束条件选取了系统的控制量、超调量和系统误差，以式（6）作为目标函数：

式中：u（t）为控制器输出；e（t）为系统误差；e1（t）为被控对象在 t此刻和（t-1）时刻输出值之差；ω1、ω2、ω3为权值，这里分别取0.98、0.001和2，以便压制系统超调量。

因为一般遗传算法要求适应度为最值，所以要对适应度函数进行转化，求取最大值。目标函数取为

3）选择操作

轮盘赌法可以提高搜索效率，因此先利用这种方法进行选择，然后将最佳个体复制到子代中，其余个体按适应度所占的比重进行交叉运算。

4）交叉和变异

标准的遗传算法采用固定值作为交叉和变异操作的概率值，缺点是不能满足算法在寻优不同阶段的不同要求。在算法初期，个体之间差异大，大一点的交叉概率和小一点的变异概率较为合适。后期随着个体之间的差异逐渐减小，应该适当降低交叉概率，加大一点变异概率，以确保最优个体被保留。因此，采用自适应的交叉和变异概率，公式为

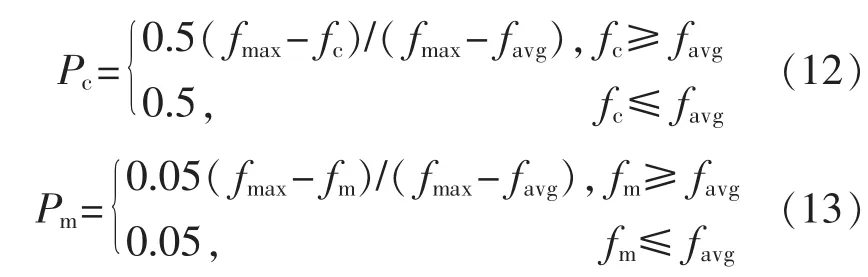
式中：Pc为交叉概率；Pm为变异概率；fmax、favg为此时刻种群的适应度的最大值和平均值；fc，fm分别为要进行交叉运算和变异运算的种群个体的适应度值。

2.3 遗传算法优化结果

优化后的隶属度函数如图5～图8所示。

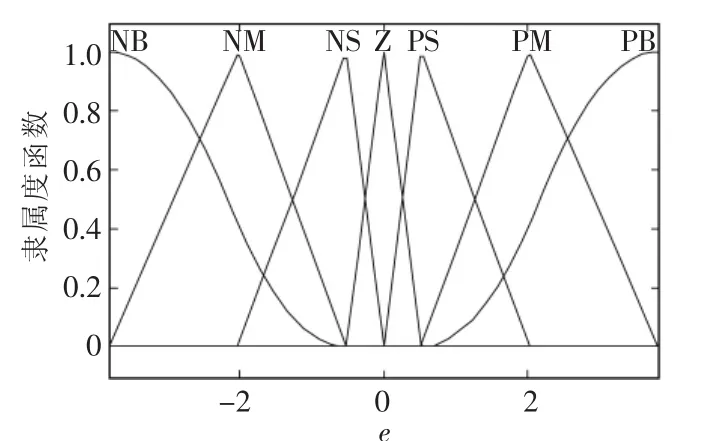
图5 优化后误差e的隶属度函数Fig.5 E error membership function after optimization

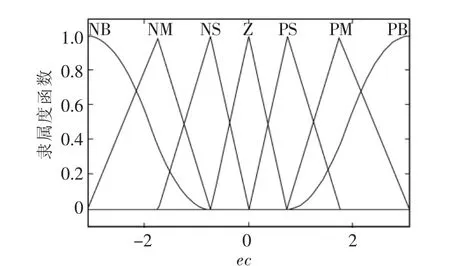
图6 优化后的ec的隶属度函数Fig.6 Ec membership function after optimization

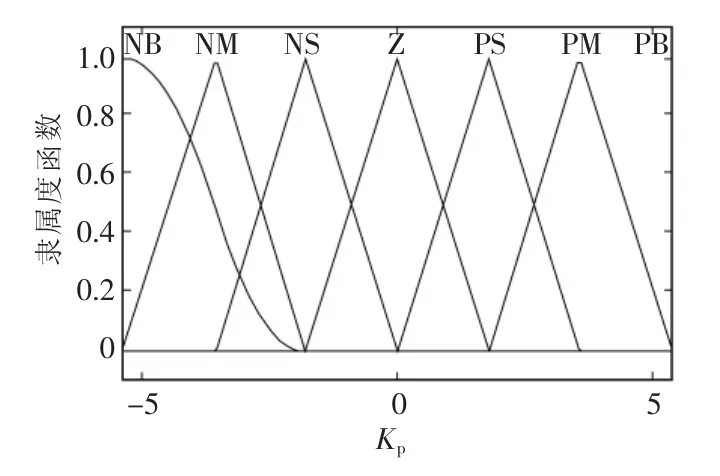
图7 优化后的ΔKp的隶属度函数Fig.7 ΔKpmembership function after optimization

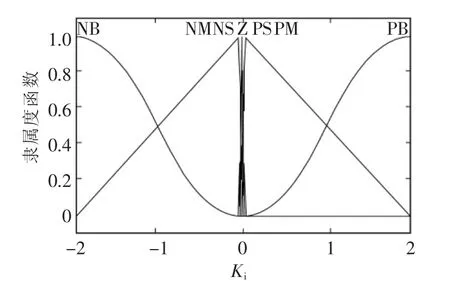
图8 优化后的ΔKi的隶属度函数Fig.8 ΔKimembership function after optimization

3 系统仿真

在Matlab/Simulink中搭建PWM网侧整流器仿真。仿真参数设置如下：交流侧的电感L值设为5 mH，交流侧的电阻R的值设为0.05 Ω，直流侧的电容C的值设为2200 μF，直流电压 Udc为 600 V，负载 R的值设为10 Ω，采样时间Ts的值设为0.0001 s。

直流侧电压Udc的仿真波形如图9所示。

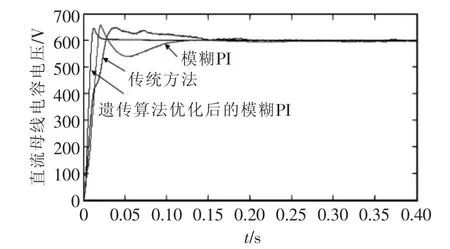
图9 直流侧电压Udc的仿真波形Fig.9 Simulation of DC voltage waveform

a相电压电流仿真波形如图10所示。

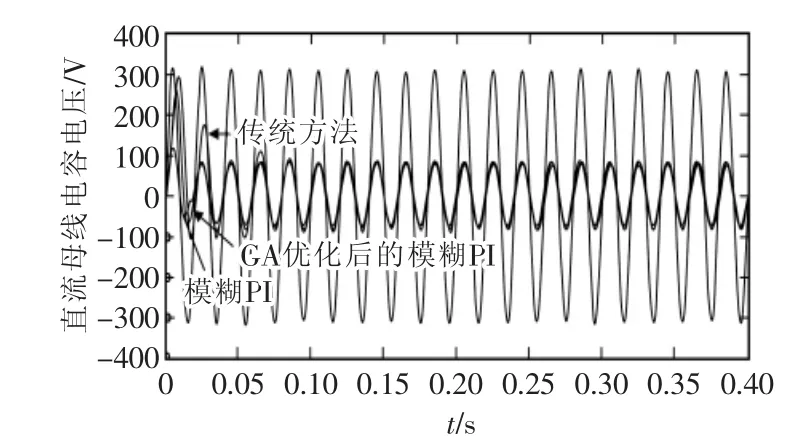
图10 a相电压电流仿真波形Fig.10 A phase voltage and current simulation waveforms

由图9可知，3种方法相比，在超调量上差距不大，但在调节时间上，遗传算法优化后的模糊PI明显优于模糊PI和传统PI，具有响应快，稳定性好的控制性能。从图10可以看出，新方法的电网电流能更快地稳定，但差距并不大。

在0.3 s处，让变流器由整流状态转换到逆变状态，其波形如图11所示。

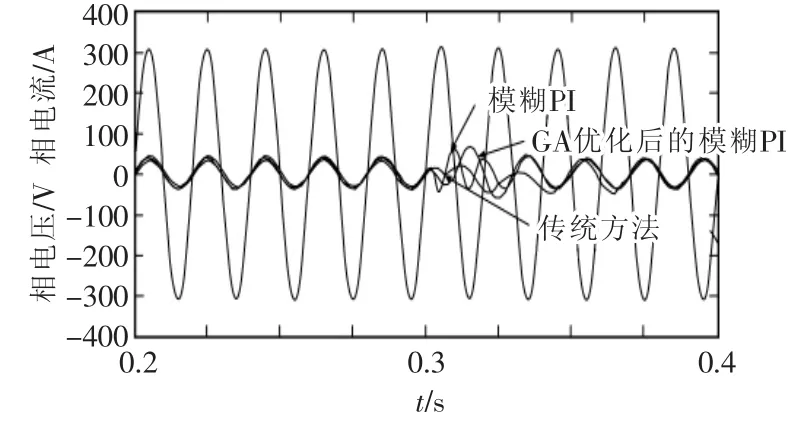
图11 整流到逆变状态的a相电流Fig.11 Rectifier state transition to inverter state of a phase current

当变流器由整流状态过渡到逆变状态时，GA优化后的模糊PI比传统PI和模糊PI需要的时间更短，大约为1个周期，模糊PI大约需要1.5个周期，传统PI需要2～3个周期。

为了测试本文设计控制器的鲁棒性，对系统负载施加扰动，仿真结果如图12所示。R在0.4 s时突然增大1倍。

图12 负载变化时的直流母线电压Fig.12 DC-bus voltage when the load changes

采用新方法的直流母线电压只出现了很小的波动，并且很快趋于稳定，而模糊PI和传统PI方法从负载变化开始就产生明显波动，大约0.05 s后逐渐稳定。直流母线电容电压随着负载突变变化小，鲁棒性好。

4 结语

本文提出的双馈风力发电系统网侧变流器的新控制方法，在电网正常情况下，其响应速度以及系统稳定性明显优于传统PI和模糊PI，变流器工作状态转换时，新方法适应更快，并且更能适应负载扰动。仿真表明对于提高直流母线电压的稳定性有比较明显的效果。

[1]赵清声，王志新.双馈风力发电机组系统接入与稳定运行仿真[J].电网技术，2007，22（31）：69-74.

[2]I Erlich，J Kpetschmann，J Fortmann，et al.Modeling of wind turbines based on doubly-fed induction generators for power system stability studies[J].IEEE Transactions on Power Systems，2007，22（3）：909-919.

[3]Pena R.，Cardenas R.，Escobar E.，et al.Control system for unbalanced operation of stand-alone doubly fed induction generators[J].IEEE Transactions on Energy Conversions，2007，22（2）：544-545.

[4]姜卫东，吴志清，李王敏，等.电网不对称时抑制负序电流并网逆变器的控制策略[J].电工技术学报，2015，30（16）：77-84.

[5]张迪，魏艳君，马利轩，等.不平衡电网电压下基于滑模变结构控制的双馈风电系统网侧变流器控制策略[J].电工技术学报，2015，30（10）：266-275.

[6]王萌.电网故障下双馈风力发电系统功率变换器运行控制[D].天津：天津大学，2012.

[7] 赵振波，李和明.单位功率因数PWM整流器双闭环PI调节器设计[J].电工技术杂志，2003（5）：68-71.

[8]曹建秋，徐凯.遗传算法优化的模糊+变论域自适应模糊PID复合控制策略[J].信息与控制，2011，40（1）：44-49.