基于线误差的机器人运动学参数标定

薛志奇，牛雪娟，王 添

（天津工业大学 机械工程学院，天津 300387）

现代制造业对工业机器人性能的要求不断提高，尤其是高精度的工业机器人。评价工业机器人性能指标主要有2个，重复定位精度和绝对定位精度。机器人的重复精度一般较高，可达0.1 mm，而绝对定位精度却较低，一般是厘米级[1]。影响机器人绝对定位精度的误差的主要因素包括几何误差和非几何误差，几何误差主要是由机器人连杆参数的不准确引起的，约占总误差的80%；非几何误差主要由环境因素、机械热变形等引起，约占总误差的20%[2]。提高机器人绝对定位精度主要有2个途径，其一是减少误差源，最大限度地提高机器人零部件的设计、加工和装配精度。由于目前数控机床大的加工精度已经很高，这种方法实现起来比较难，而且成本高。其二是用标定技术修正误差，这种方法能使机器人的绝对精度大幅提高，运用比较广泛。

机器人标定是运用适当的测量手段和参数求解方法求出机器人模型的参数，以提高机器人绝对精度的过程。文献[3]将机器人的标定划分为关节级标定、机器人运动学标定、动力学标定。其中，连杆参数的运动学标定与测量工具的选用以及测量方法有很大的关系。随着测量技术的不断提高，国内外学者采用了各种新兴的测量工具和测量方法对机器人进行参数标定[4-7]。既有标定方法的精度都不高，尤其是采用的测量方法，实用性不是很强，而且过程比较复杂。在此，通过建立运动学误差模型，创新地采用拉绳编码器对机器人进行距离测量，提出基于线误差的机器人运动学参数标定方法，并通过试验验证该方法能提高机器人的绝对定位精度。

1 基于线误差运动学标定模型

1.1 基于线误差标定平台的建立

如图1所示为基于线误差的标定平台构成。将拉绳编码器的位姿标记为｛U｝，机器人底座标记为｛B｝，工具坐标系标记为｛T｝。 其中，｛U｝为用户坐标系，｛B｝为基础坐标系，且｛U｝与｛B｝的方向平行，｛T｝与法兰坐标系的方向平行。

图1 基于线误差标定平台Fig.1 Calibration platform based on linear error

1.2 线误差模型的描述

机器人末端被测点Pi在机器人用户坐标系｛U｝中的实际位置其距用户坐标系原点Pu的距离为PuPi，而拉绳编码器实际测得的拉绳长度为PuPi′。在此把机器人被测点到用户坐标系原点的实际距离和指令距离之间的误差称为线误差，可表示为

1.3 六自由度机器人MDH运动学模型

DH[8]模型描述工业机器人连杆坐标系采用αi，θi，ai，di4个独立的参数。其不足之处是当2个相邻的关节的轴线平行时，平行度的轻微偏差，会导致实际的公法线的位置与理论的公法线的位置有一个很大的偏差。故在此选用MDH[9]模型建立运动学模型，它的特点是在DH模型的基础上增加了一个绕Y轴旋转的角度βi，当实际几何参数存在微小变化时，这一附加项能够表达出系统的模型特征，当相邻关节轴线不平行时，转角βi值定义为零。按照MDH运动学模型，建立机器人各连杆空间坐标系，如图2所示。

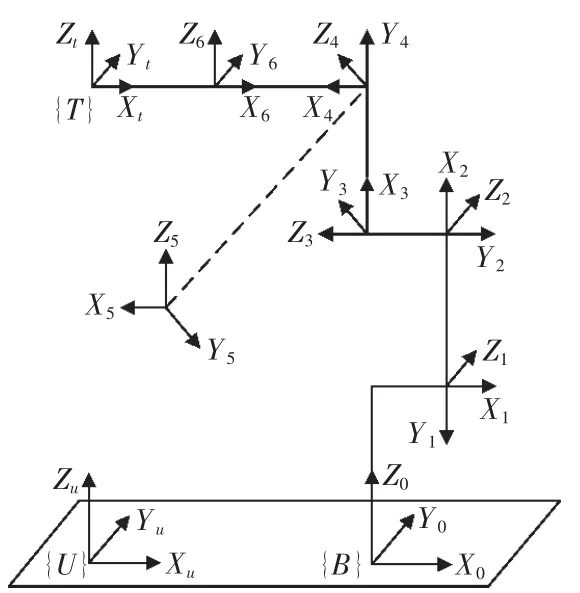
图2 连杆坐标系示意Fig.2 Schematic diagram of coordinates

机器人各连杆变换矩阵为

式中：连杆编号 i=1，2，…，6；c=cos；s=sin。

机器人末端法兰坐标系相对基础坐标系的变换矩阵为

为简化算法，将工具坐标系｛T｝的坐标轴指向设置为法兰坐标系的坐标轴指向；用户坐标系｛U｝的坐标轴指向设置为基础坐标系 ｛B｝的坐标轴指向。则机器人的工具坐标系到法兰坐标系和基础坐标系到用户坐标系的齐次变换矩阵分别为

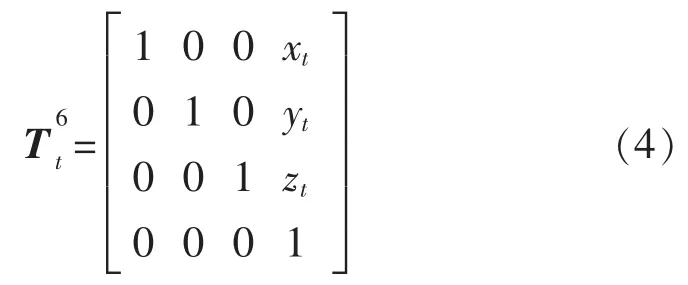
式中：xt，yt，zt分别为工具坐标系原点在法兰坐标系中的坐标值。

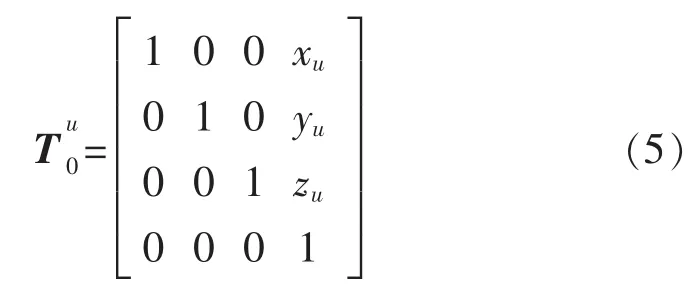
式中：xu，yu，zu分别为机器人基础坐标系原点在用户坐标中的坐标值。

由式（3）、式（4）、式（5）可知机器人工具坐标系原点在机器人用户坐标系中的位姿为

1.4 六自由度机器人MDH误差模型

由式（2）可知，串联机器人的每个连杆参数的名义值和真实值之间是有微小差别的，用δαi，δai，δdi，δθi，δβi分别表示 2 个相邻连杆间的扭角偏差、连杆长度偏差、连杆偏置偏差、关节角偏差和连杆转角偏差。基于这些偏差都是比较小的事实，可以用微分偏差来表示。用AiN和AiR分别表示连杆i的名义变换和实际变换，Δi表示相对于当前连杆i坐标系的微分变换，则连杆i的误差为所有几何参数的误差的叠加[10]为

式中：AiN为式（2）所表示的第i个连杆的MDH连杆模型。dAiN可以由变换矩阵Ai求得

由式（8）知：

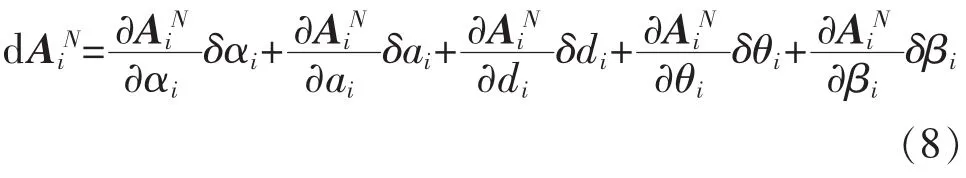
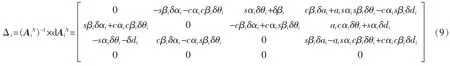
因为机器人用户坐标系和基础坐标系的方向是平行的，所以用户坐标系到基础坐标系的变换矩阵的误差矩阵为

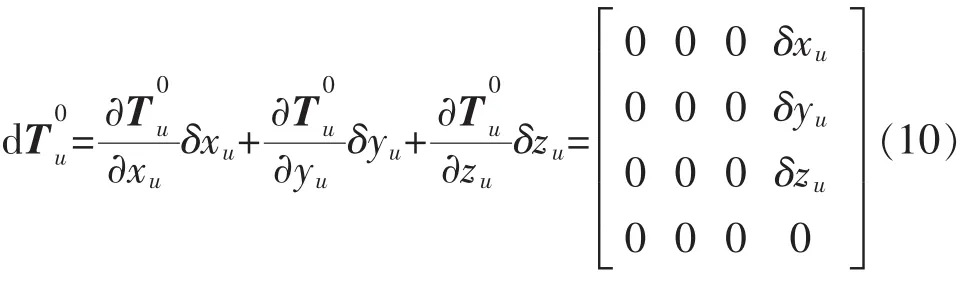
同理，因为工具坐标系和法兰坐标系方向平行，所以机器人法兰坐标系到工具坐标系的变换矩阵的误差矩阵为

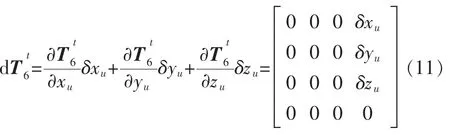
2 线误差标定算法推导及求解

2.1 机器人连杆误差与绝对定位精度的关系

串联机器人每一关节均有参数误差存在，各关节参数误差传递到机器人的工具末端点，对于机器人每个连杆，由式（3）和式（9）可以得到机器人末端法兰坐标系相对基础坐标系的实际坐标变换为

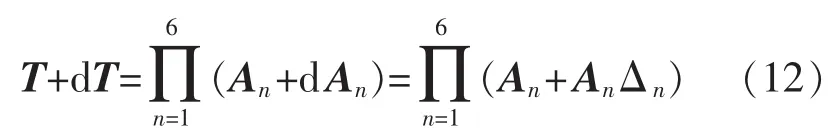
将该式展开略去所有高阶微分项可得到：

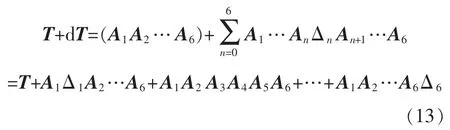
将式（2）、式（3）、式（9）带入式（13）并且经过大量的化简可以得到如下形式[11]：

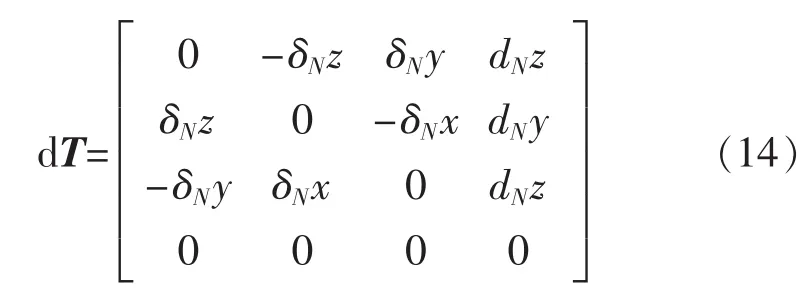
式（10）左上角的3×3矩阵为姿态微动量，第4列的前3行的3个元素为位置微动量。即：

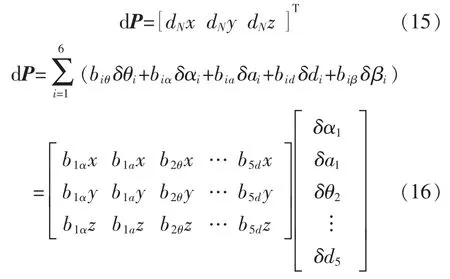
令

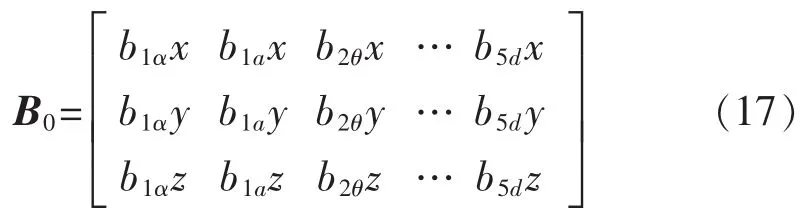
为各个连杆参数误差的系数误差矩阵

为机器人所有连杆参数的固有误差向量。因为建立的用户坐标系和机器人基础坐标平行，所以基础坐标系相对与用户坐标系中的位置误差矩阵为

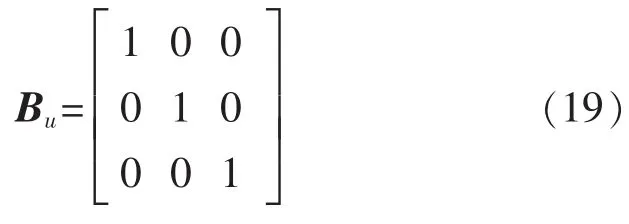
误差向量为

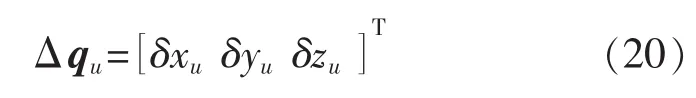
工具坐标系相对法兰坐标系的位置误差矩阵为

误差向量为

综上所述，由式（17）、式（19）、式（21）可以得到所有要标定的参数误差矩阵为

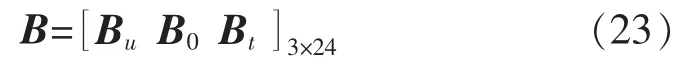
由式（18）、式（20）、式（22）可以得到所有的固有向量为

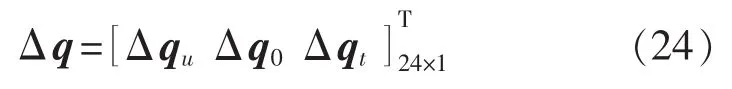
式中：用户坐标系待标定参数为 δxu，δyu，δzu。 因为用户坐标系和基础坐标系平行，相关参数的误差之间存在耦合，这样连杆 1待标定的参数只有δα1，δa1。因为坐标系只有连杆2和连杆3之间存在轴线平行，所以只有连杆转角偏差δβ2。这样，连杆2需要标定的参数有 δα2，δa2，δθ2，δβ2；连杆 3 待标定的参数都为δα3，δa3，δθ3，δd3；连杆 4 待标定的参数为 δα4，δa4，δθ4，δd4；连杆 5 待标定的参数为 δα5，δa5，δθ5，δd5。 对于连杆6，因为法兰坐标系和工具坐标系平行，所以工具坐标系的待标参数和6杆的待标参数耦合工具坐标系的待标定参数为 δxt，δyt，δzt。这样 Δ 中总共就有24个需要标定的参数。

2.2 标定算法推导

假设机器人工具末端在机器人用户坐标系｛U｝中的理论位置为而实际的指令位置为则整体的机器人线误差标定模型可以用图3来表示。

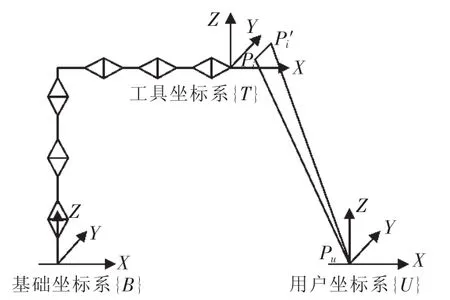
图3 线误差标定模型简图Fig.3 Linear error calibration model diagram

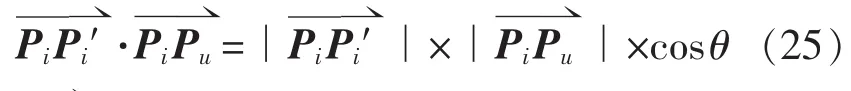
这是一个含有24个未知数的方程。

2.3 参数求解

由式（26）可知，用于标定机器人参数的线性方程组中包含24个参数。至少需要24个方程才能求出方程的最小二乘解。由于该方程的条件数很大，可以采用奇异值分解 （SVD）的方法求得最小二乘解。为了尽可能减小SVD误差，实验中采样点应尽可能涵盖机器人的工作空间。

3 试验分析

3.1 试验过程

使用拉绳编码器对课题研究的某型六自由度工业机器人进行运动学标定。试验选用的是美国西克公司BCG-E1BM0399型拉伸编码器，其拉绳长度3 m，精度0.015 mm。这是一种带有Ethercat接口的拉绳编码器，可以直接连接到计算机上，工作时计算机能实时读取机器人的每个连杆的关节值和拉绳长度。试验时，手动控制机器人的每个关节运动，操作机器人以不同的姿态在机器人的工作空间运动，并且使机器人在工作空间尽可能大范围地获取采样点。这样获得的每一个采样点都包含有机器人的每一个连杆的关节角 θi（i=1，2，…，6）及拉绳的长度Li，如此至少获得50个采样点，然后按照上面参数求解方法求得最小二乘解即为连杆的几何参数补偿量。

3.2 试验结果

标定前、后的参数如表1所示，经过参数求解可以很好地得到机器人的补偿后的连杆参数，如表1最后一列所示。

该算法标定实验过程中，标定仪的摆放位置是任意的，且拉绳末端在法兰盘上的位置也是任意的。整个标定过程方便简单。经过反复试验，该算法零点误差精度为0.1°，连杆几何参数误差精度可精确到3.15 mm以下，线误差平均缩小了75%。机器人绝对定位精度由厘米级提高到毫米级。

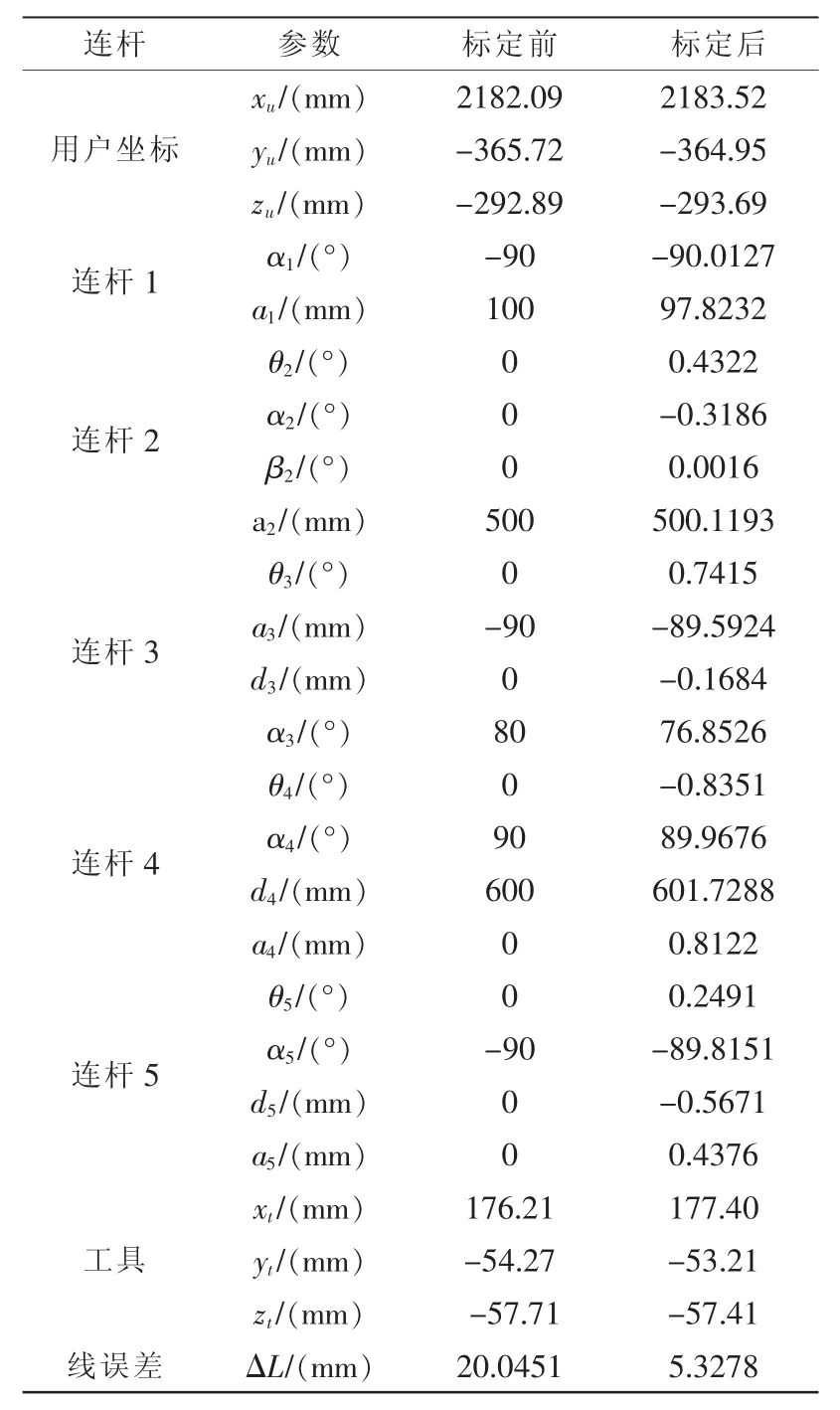
表1 标定前和标定后连杆几何参数Tab.1 Geometrical parameter of links before and after calibration

4 结语

采用高精度拉绳编码器对某型六自由度工业机器人进行测量，并对其运动学参数进行标定。研究过程中，基于机器人的MDH运动学模型，建立了机器人各坐标系间的平行关节的齐次变换误差模型；在此基础上，推导了基于线误差的运动学标定模型；经过SVD分解后得到补偿量，对关节参数进行补偿。线误差的引入，避免了传统测量仪器成本高，操作难度大，测量误差大等缺点。试验结果表明，基于线误差的机器人运动学标定可以明显地提高机器人的绝对精度。其中，线误差平均缩小75%，机器人的绝对精度由原来的厘米级提高到毫米级。

[1]周翔，杜姗姗.工业机器人零位标定点约束分布研究[J].计算机工程，2015，41（12）：265-274.

[2]齐飞，平雪良，刘洁.关于工业机器人标定方法的研究[J].机床与液压，2015，43（21）：32-36.

[3]Roth Z，Benjamin W，Mooring，Bahram R.An overview of robot calibration[J].IEEE Journal of Robotics and Automation，1987，3：377-385.

[4]杨丽红，秦绪祥，蔡锦达，等.工业机器人定位精度标定技术的研究[J].控制工程，2013，20（4）：785-788.

[5]H Wang，M Jiang，W Chen.Visual servoing of robots with uncalibrated robot and camera parameters[J].Mechatronics，2012，22（6）：661-668.

[6]许辉，王振华，陈国栋，等.基于距离精度的工业机器人标定模型[J].制造业自动化，2013，35（6）：1-4.

[7]龚星如.六自由度工业机器人运动学标定研究[D].南京：南京航空航天大学，2013.

[8]Mahmoud Tarokh，Huy Dang Ho，Antonios Bouloubasis.Systematic kinematics analysis and balance control of high mobility rovers over rough terrain[J].Robotics and Autonomous Systems，2013，61（1）：13-24.

[9]J Armstrong Piepmeier，P A Morgan.Uncalibrated vision-based mobile robot control[J].Space&Robotics，2014，21（5）：388-395.

[10]陈钢，贾庆轩，李彤.基于误差模型的机器人运动学参数标定方法与实验[J].机器人，2012，34（6）：680-688.

[11]任永杰，邾继贵，杨学友.基于距离精度的测量机器人标定模型及算法[J].计量学报，2008，3（29）：198-202.