模型缩减法在转子动力学中的应用比较

模型缩减法在转子动力学中的应用比较

黄健伟，罗贵火，王飞

(南京航空航天大学能源与动力学院，江苏南京210016)

摘要：随着大规模模型的不断增加，模型缩减在动力学分析中显得越来越重要，模型缩减在保证精度的基础上可以减少存储空间和提高计算效率。常见的模型缩减法主要有静态缩减法(Guyan)、动态缩减法(Dynamic reduction)、改进的缩减系统法(IRS)、系统等价扩展缩减法(System equivalent expansion reduction process)以及部件模态综合法(CMS)。从理论上介绍了几种模型缩减法的不同，而且通过这几种方法对有限元法建立的简单单转子系统进行临界转速的分析，比较分析它们在准确度以及计算效率的差别。结论：1)在计算效率和准确性上，IRS法和CMS法表现较好；2)静态缩减法只在零频时结果精确，可靠性较差；动态缩减法在特定频率下结果较精确；SEREP法计算结果比静态缩减法和动态缩减法要精确，但是精度和计算效率低于CMS法和IRS法；3)CMS法在预测高频运动时结果更准确。

关键词:模型缩减计算效率单转子准确度

中图分类号：V231.96文献标识码：A

作者简介：黄健伟(1988-)，男，南京航空航天大学能源与动力学院，硕士研究生，主要研究方向：结构强度与完整性。

收稿日期：2014-12-24

Comparison study of application of model reduction in rotor dynamics

HUANG Jianwei,LUO Guihuo,WANG Fei

Abstract:As more and more large models are adopted in practice, model reduction becomes an important issue in rotor dynamics. Based on accurate prediction, model reduction can reduce storage and simulation time. The typical methods are Guyan reduction, dynamic reduction, improved reduce system(IRS), system equivalent expansion reduction process and component mode synthesis method. A shaft-line model of a single rotor system is established with the finite element method. By analyzing the dual-rotor system of its analogous dynamic characteristics, the accuracy and computation efficiency of different methods are compared. The results are as the following：1)Compared with different reduction methods, IRS and CMS deliver the best eigenfrequency results.2)Guyan reduction is only exact at zero frequency，dynamic reduction can be exact at the chosen frequency， SEREP method is better than Guyan reduction and dynamic reduction in accuracy, but when predicting high frequency motion it is less accurate and less efficient than CMS and IRS method.3)CMS method has better accuracy in predicting high frequency motion.

Keywords:model reduction; computation efficiency; single rotor system; accuracy

1研究背景

近些年来，随着模型尺寸的增大，动力学分析所需计算时间和存储空间都不断增多，降低了工作效率和增加了计算成本。模型缩减的方法在保证结果准确度的基础上可以很好的提升计算效率和减少存储空间。模型缩减法得到了迅速的发展，主要有静态缩减法、动态缩减法、改进的缩减系统法、系统等价扩展缩减法以及部件模态综合法。所以研究各种模型缩减方法求解精度的特点和计算效率都非常重要。

2模型缩减法的介绍

用于转子系统分析的一种常见的空间离散化的方法是有限元法。转子系统的二阶运动微分方程如下：

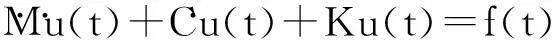
(1)

其中M，C，K∈Rn×n分别是系统矩阵中的惯性矩阵，阻尼矩阵和刚度矩阵。f(t)∈Rn×1，是外部载荷，q∈Rn×1是状态向量。模态缩减的一般概念是，找到一个低维数子空间T∈Rr×n通过映射近似状态向量。通过对子空间的预测，可以得到一个低维的二阶运动微分方程

(2)

其中Mr=TTMT，Cr=TTCT，Kr=TTKT是缩减后系统的矩阵，fr(t)=TTf(t)是转换后的外力载荷。这种维数缩减方法的效果和精确度都取决于ε的规模。基于对转换矩阵T的选择，不同的缩减技术在过去几十年中已经得到了发展。

2.1Guyan缩减法

Guyan缩减法[1]，也叫静态缩减法，它的特点是将与被缩减掉的自由度相关的惯性项和阻尼项都忽略。状态向量q和载荷向量f，以及系统矩阵M和K被拆分为主自由度和从自由度。不受外力的自由度被选择作为从自由度。假设阻尼时可忽略，运动方程组可以重新写成：

(3)

下标m和s分别对应主坐标系和从坐标系。忽略掉第二个方程的惯性项，从自由度可以被消除，如下：

(4)

其中矩阵Ts表示缩减前状态向量和主坐标系之间的静态转换矩阵。

缩减后的质量矩阵和刚度矩阵如下：

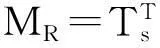
(5)

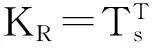
(6)

一般地说，Guyan缩减法可以很好地接近低阶特征值，事实上它只有在零频时是精确的。对于高频运动，惯性项的影响是非常大的，这种情况下Guyan法就显得不精确了。

2.2动态缩减法

动态缩减法(Dynamicreduction[2])是静态缩减法的一种转换或者扩展，在任意指定频率下的缩减都是准确的。假设指定在ω0处进行降维缩减，对于方程组(3)中的第二个方程，惯性力可以写成如下格式：

(7)

所以缩减转换可以写成如下

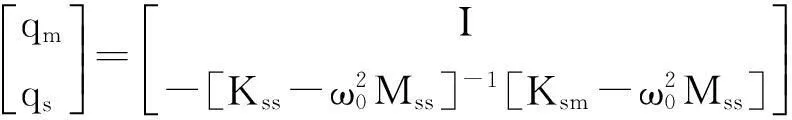
=Tdqm

(8)

动态缩减法对于高频率运动相对准确，但是需要认真选择初始频率ω0。

2.3改进的缩减系统方法

改进的缩减方法(IRS[3])考虑惯性力，将一个惯性项加到静态缩减转化矩阵中。这个惯性项使得结果能更加接近未缩减模态的模态向量，惯性项可以通过静态缩减法得到。

Gordis[4]利用二项式定理得到IRS法的转换矩阵。对于一个已给的频率ω,通过方程组(3)可以得如下方程：

[Kss-ω2Mss]qs=-[Ksm-ω2Msm]qm

(9)

这个方程和方程(8)很相似。通过二项式定理，方程(9)可以被整理成：

qs=-[Kss-ω2Mss]-1[Ksm-ω2Msm]qm

(10)

式中o(ω4)表示ω4的误差。忽略误差，考虑到IRS方法是基于静态缩减法，重新整理方程(10)，得到：

(11)

(12)

(13)

缩减后的质量和刚度矩阵可以写成：

(14)

(15)

相关参量可以通过Guyan法中得到，通过方程(12)可以得到IRS法的转换矩阵。

2.4系统等价扩展缩减法

系统等价扩展缩减法(SEREP[5])使特征向量的子集为Φr转换矩阵可以写成T=Φr。通过这种变换，物理坐标系被转换为模态坐标系。系统等价扩展缩减法(SEREP)也利用特征向量的子集。通过用主自由度和从自由度划分物理坐标系和特征向量，物理坐标系被保留下来。这个转换矩阵被写成

(16)

其中Φr=[ΦmΦs]T表示被分离的特征向量的子集。

所以转换矩阵被写成

(17)

为了得到转换矩阵，首先要得到无阻尼系统的特征向量。然后，TSEREP和缩减后的质量和刚度矩阵可以通过方程(17)-方程(19)得到。

(18)

(19)

与动态缩减法和静态缩减法相比较，SEREP法在有预先定义的约束的系统的高频运动中预测得更好。

2.5部件模态综合法

固定界面模态综合法(CMS)由Craig和Bampton[6]提出,并由Craig和Petyt[7-10]进一步研究。先要将模型分割为两部分，包括外部结构和内部结构两种。通过分割，物理坐标被分为与主自由度和从自由度相对应的外部坐标和内部坐标。类似于方程(3)和(4)，模态综合法的约束模态由下面的方程决定：

0=Ksmqm+Kssqs

(20)

(21)

Φc是约束模态。主模态从下面的方程计算得到

KssΦ=λMssΦ

(22)

其中Φ表示特征向量，λ是特征值。Φ通过模态截断处理，Φ剩余的子集可以写成Φr。

最后，通过Craig和Bampton的基本假设，从自由度的位移如下

qs=Φcqm+Φry

(23)

因此，转换过程如下

(24)

转换矩阵为

(25)

对于缩减后结构，固定界面模态综合法计算结果更好。但是忽略主模态的高阶项，可能导致结果的不精确。

3各种缩减法的结果比较

本文针对单转子模型，利用上述介绍的几种模型缩减法对其进行动力学分析，并对各种方法得到的结果进行比较分析。用有限元单元方法建立单转子系统轴线的模型，采取Timoshenko梁单元。阻尼和内部摩擦力被忽略。模型包括了21个单元，22个节点和88个自由度。模型的图解和支承的位置见图1。

图1　单转子系统图

转子系统不受外力的情况，转子系统的运动方程可以写成：

(26)

其中Ω是转速，G是陀螺力矩矩阵。对于这个转子系统，节点1，5，13，18，22的自由度被选作为静态缩减法、动态缩减法、IRS法和SEREP方法的自由度。对于固定界面模态综合法来说，只有节点5和13的自由度叫做主自由度。为了比较不同方法的计算效率，需要选择前12阶模态作为保留模态，使得方程(24)中CMS法的坐标转化后的矩阵变为一个20×1矩阵，这样可以保证缩减后的维数和通过其他缩减方法缩减后的维数相同。

3.1临界转速的比较

对于缩减模态和全模态，特征值和特征向量以及和坎贝尔图都通过计算得到。不同方法得到的坎贝尔图如图2(a)-(f)。尽管在不同方法得到的结果之间只存在微小的不同，但在图2中还是可以看到不同。

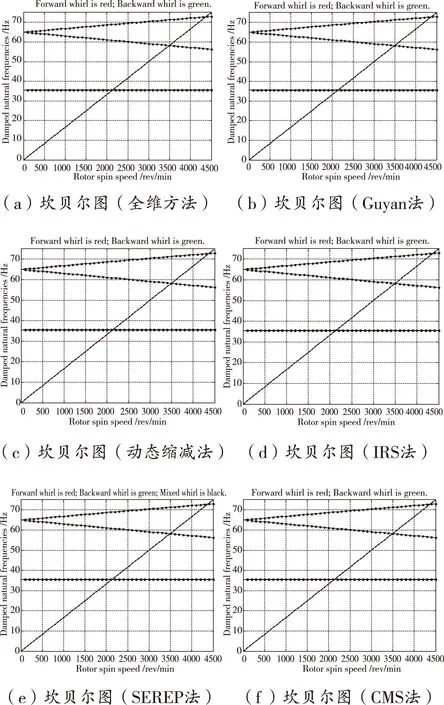
图2　由不同缩减法得到的坎贝尔图

从表1可以看出动态缩减法得到的一阶正进动和一阶反进动的临界转速比Guyan静态缩减法要精确，这是由于方程(7)中合适的选择了ω0的值。在这个例子中ω0=220 rad/s≈35 Hz。对于高维数复杂转子系统，选择一个合适的值不是一个简单的任务，尽管反复计算会降低计算效率，但是为这个参数的选择提供了帮助。

同样从表1还可以看出，和未缩减方法相比，改进的系统缩减法(IRS法)和系统等价扩展缩减法(SEREP法)得到的结果更加精确，尽管在计算单转子高频运动时会出现一些误差，本文在后面的章节将会讨论这些误差。

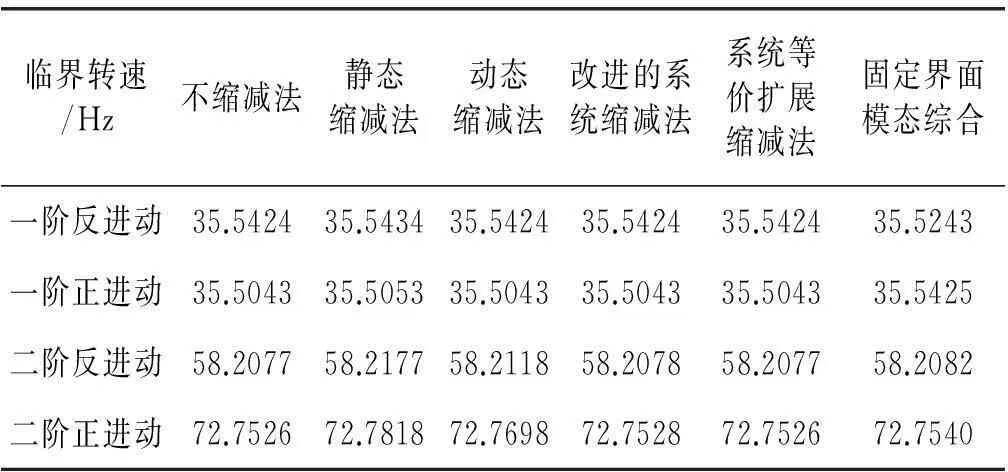
表1　临界转速比较

3.2特征频率的比较

前14种特征频率的不同在图3中表示出来。特征频率的差值被定义为：

eigdiff=eigreduced-eigfull

(27)

图3　各种方法的特征频率之间的差值

图3中所有特征频率之间的差值都是正值，正好符合缩减法得到的频率比未缩减方法得到频率更高的理论。对于不同的缩减方法，尽管动态缩减法在选定频率下得到的结果更好，但静态缩减法和动态缩减法的结果几乎完全一致。这两种方法对于在高频运动的计算结果都不可信。图3中可以看出，固定界面模态综合法(CMS)和改进的系统缩减法(IRS)在对高频运动计算的结果都比其他缩减方法要更精确。但是，对于固定界面模态综合法，选择哪种更低维特征向量和为了得到Craig -Bampton约束模态的方程(23)需要多少维数的特征向量，会降低计算的效率。但是，对于CMS法，要为方程(23)中约束模态选择哪种维数更低的特征向量和多少维数的特征向量是很必要的，但这会降低计算的效率。

3.3模态置信准则

通过未缩减模型和缩减模型得到的特征值，转子系统的特征向量和振型都可以得到。为了评估未缩减模型和缩减模型之间的关联程度，需要得到模态置信准则[11]。MAC可以表达成：

(28)

其中Φi表示未缩减模型第i个特征向量，Φj表示第j个扩展的特征向量。

特征向量的维数一定是相同的，所以缩减后的特征向量可以通过转化矩阵扩展成原自由度数下的特征向量。在MAC矩阵中的所有值都在0到1之间。这个值越小，特征向量之间的相关性越差，如图4所示。

(a)各方法得到的MAC值比较　(b)MAC值比较(IRS法和CMS法) 图4　MAC值比较

通过观察图4(a)和(b)，静态缩减法(Guyan缩减法)和动态缩减法的MAC值是一致的。与另外三种方法相比，IRS法和CMS法与未缩减模型的相关性更好。MAC比较结果和特征频率的比较结果一致。

3.4计算效率的比较

使用MATLAB对所有方法进行编程，运行100次记录需要的时间。每种方法平均耗费时间被列在表2中，不同方法被列在图5中。

表2　每运行100次程序的平均时间

如图5和表2中的内容，和未缩减模型相比，所有的缩减法都有比较高的计算效率。对于上面提到的单转子系统，几乎可以省下90%的计算时间，同时又能保证较好的仿真程度。

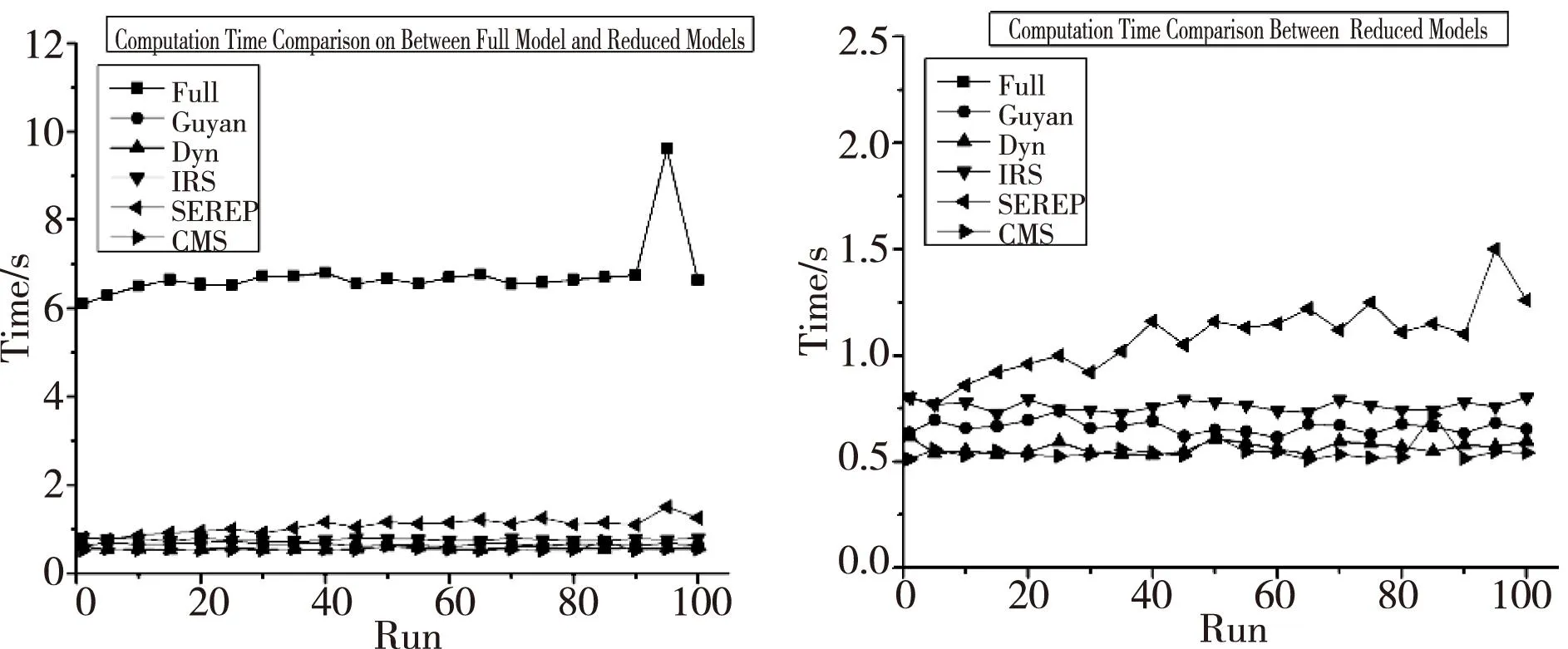
(a)不缩减法和缩减法的比较　(b)各缩减法之间时间的比较 图5　计算效率的比较

在图5(b)中，固定界面模态综合法和动态缩减法是最有效率的，其次是Guyan缩减法，IRS法以及SEREP法。当同时要考虑效率和精确度的时候，对于本文中的单转子系统，固定界面模态综合法是最合适的。

4结论

本文对几种不同的模态缩减的方法进行了比较。对特征频率比较后发现，改进缩减系统法(IRS法)和固定界面模态综合法(CMS法)得到的特征频率效果最好。相对来说，Guyan静态缩减法是相对来说准确性较差，而且计算效率最低，因为静态的本质是只在零频的时候才是精确的。静态缩减法和动态缩减法的不同在于，动态缩减法在选定的频率处是精确的，而不是在零频处。但是，动态缩减法选择一个合适的频率很繁琐。SEREP法比Guyan法和动态缩减法都更加准确，但是当计算高频运动时固定界面模态综合法和IRS法比SEREP法要更加准确和有效率。对于本文中单转子系统，固定界面模态综合法和IRS法在精确性上几乎是一样的。但是CMS固定界面模态综合法在计算高频运动时更加精确。

参考文献

[1]J. Guyan. Reduction of stiffness and mass matrices[J]. AIAA, 1965.3(2):380

[2]Mario Paz. Dynamic condensation.AIAA, 1984,22(5):724-727

[3]J.C.O’CALLHAN. A procedure for an improved reduced system (IRS) model. Proceedings of the 7th International Modal Analysis Conference, Las Vegas, January 1989：17-21

[4]JGordis, Joshua H. An analysis of the Improved Reduced System (IRS) model reduction procedure

[5]C.V.S. Sastry,D. Roy Mahapatra,S. Gopalakrishnan. An iterative system equivalent reduction expansion process for extraction of high frequency response from reduced order finite element model. Computer Methods in Applied Mechanics and Engineering. 2003, 192(15):1821-1840

[6]R.Craig, M.Bampton. Coupling of substructures in dynamic analysis.AIAA,6,1968

[7]R.Craig. Coupling of substructures for dynamic analyses: an overview. AIAA-2000-1573

[8]R.Craig, C.J.Chang. Free-interface methods of substructure coupling for dynamic analysis. AIAA,12,1976

[9]Daniel Rixen. A dual Craig-Bampton method for dynamic substructuring. Journal of Computational and Applied Mathematics,2004,168(1-2):383-391

[10]Daniel Rixen,Charbel Farhat,Michel Géradin. A two-step, two-field hybrid method for the static and dynamic analysis of substructure problems with conforming and non-conforming interfaces. Computer Methods in Applied Mechanics and Engineering, 1998,154(3-4):229-264

[11]Randall.J.A. The modal assurance criterion-twenty years of use and abuse.Sound and Vibration, August 2003：14-20