会提问题的孩子聪明

赵薇萍

【现象扫描】

《义务教育数学课程标准（2011年版）》在总目标中提出“增强发现和提出问题的能力、分析和解决问题的能力”，没有问题的提出，就谈不上问题的解决。

爱因斯坦曾经说过：“提出一个问题比解决一个问题更重要。”因为解决问题是学习或实验上的技能，而提出新的问题，从新的角度去看旧的问题则需要创造性的想象力。刚入学的孩子不知道什么是数学问题，不懂数学问题怎么提。怎么让一个对数学懵懂的孩子能够敏锐地捕捉到数学信息，并提出一个合理的数学问题呢？这就是我们要研究的问题。

一年级孩子刚学提数学问题出现的问题颇多，笔者大致罗列了一下，有以下几种情况出现。

阅读理解型——

在一年级上册出现较多，不明白什么叫数学问题，提的问题和数学不沾边，如“为什么小兔要给小熊蘑菇？”把它列为阅读理解题差不多。

自说自答型——

在一年级上册出现比较明显。由于不知道什么是问题，入学不久的孩子往往把结果当作问题直接说出来了，不会明知故问，特别是结果直接呈现的那种题。如“左边有2朵花，右边有5朵花，一共有7朵花。”他们直接就数出结果来了。为什么还要提问呢？他们不明白一眼可以看到结果的还要问什么。

明知故问型——

信息已经很清晰地显示了还提问题，这样的问题显然没有思考的价值。我们要引导学生学会对信息进行筛选，重组再提出有价值的问题。统计表中已经呈现了100米赛跑的人数，就不必再去问一遍，这样的问题思维含量不足，有明知故问之嫌。

另辟蹊径型——

不会利用已获取的信息来提出相关问题，而是再去寻找信息来提问，造成信息的浪费。有学生提问：“男生有几个？女生有几个？”原来统计表中已经统计出不同运动项目参加的人数，完全可以拿来作信息，不必另起炉灶。再说，按男女分，光看图片也不好区分。我们要培养学生对信息的加工能力，问题提得好，有利于资源的调配。

类不匹配型——

一年级的教材中出现了三种类型的问题，求总数，求部分数，求相差数。数量关系都在同一类事物中展开，如人数和人数比，不能把人数和动物的只数比。即使不同类，也转换成同类来比较，如101班有38人，矿泉水有30瓶，每人一瓶够分吗？这里人数和瓶数不同类，可引导学生这样思考，38人，每人一瓶水，需要38瓶，38瓶大于30瓶，所以不够分。如棋类和球类不是同类不可比，即使比了数的大小，单位名称也不好写，写“副”还是写“只”。可以引导孩子把不同棋类进行比较 ，也可以比球类。

指向不明型

会提问，但在众多信息中，指向性不够明确。如在有多条信息时问“一共有多少本书？”具体是指谁呢？

【教学措施】

一、唤醒提问意识

培养学生提出问题和解决问题的能力，首先培养学生问题意识。问题意识主要指学生具有自主探索、积极思考、发现问题、提出问题、阐述问题等自觉的心理活动。问题意识可以激发学生的学习欲望和勇于探究的科学精神，发展学生的数学思维，深化学生对事物的认识。学生问题意识的形成，需要经历一个从敢问到爱问再到善问的过程。如果我们能营造一种平等愉快的课堂气氛，那学生就能敞开心扉，畅所欲言。这里以我平时工作中的几个案例说明如何在开放的课堂中唤醒学生的提问意识。

（一）鼓励提问

大多数的学生在学习过程中喜欢听，习惯于理解，有自己想法并敢于提出来的不多，所以课堂上老师应有意识地培养学生的问题意识，对大胆表达自己想法的同学要多鼓励。在上《20以内数的读法和写法》时，我给学生讲20这个数的个位虽然表示一个也没有，但还是要写0占位，话音刚落，奕然举手问：“老师，如果2前面表示一个也没有，这个0要写吗？”这个问题提得实在太有价值了，我马上组织大家讨论。然后我告诉大家，会提问题的孩子聪明，老师喜欢会提问的孩子，大家想到什么尽管提。于是，又有几只小手举起来了……

（二）学贵质疑

“学贵有疑，小疑则小进，大疑则大进。”课堂中，我总是小心地呵护学生提问的积极性，保护他们的好奇心。目的是使学生提问的胆子越来越大，逐步养成敢想、敢问、敢说的好习惯。例如，期末模拟试卷中有这样一道选择题，沿着梯形的高剪开，得到的两个图形不可能是（ ）。A.两个梯形；B.两个三角形；C.三角形和梯形；D.长方形和梯形。改考卷时，我也没多想，选择了B，也就是不能得到两个三角形。可我在讲解时，王哲提出来可以得到两个三角形。我没有表态，而是说，你到黑板上来画一画吧，王哲果然画成了。

我很佩服，大大地表扬了王哲。因为按照一般人的思维，选择题中至少有一个答案，这道题的其他答案容易想到，如果把这个答案否定，也就意味着这题无项可选，这大概是出题目的老师也没想到的吧。我说：“王哲很大胆地提出了与众不同的想法，老师很欣赏，数学表现加1分。”有人不服，觉得是题目本身有问题，不然，也许大家也能想到。我说：“别人想不到，王哲想到了，这就是加分的理由，我觉得加1分还不够，要加3分。今后大家也要敢于质疑，即使说错了，老师同学都会帮助你纠错，同样，你也会有一分收获，不是吗？”

平时，多给学生这样的鼓励，课堂就能充满张力与活力，学生也能带给你意想不到的惊喜。

（三）挑战权威

《数学报》内容丰富，印刷精美，深受大家喜爱，而且，很少出现错误。可这次的《数学报》却出现了这样的错误，1-2=（），对一年级的孩子来说，这是无法做的。因为是周五放学前发下的，事先我没看过，所以直到有家长来问，我才知这个问题，赶紧发校讯通更正。一位家长打电话给我说：“孩子不听话时，拿老师的话来压我们，当我告诉他这道题印错时，他说，我们老师说了，1-2=0。老师你帮我教育一下。”家长说服不了孩子，只能求助于我。我听完，哑然失笑，多可爱的孩子。还有家长说一家人正在研究这道题该怎么做。周一孩子们来上学，我觉得有必要与他们讨论一下这个问题。我说1-2不是不能做，能做，结果是负1，不过是初中内容，小学生还不需要掌握。今后碰到这种问题，要请教长辈，不能想当然。大家不要迷信课本一定是对的，报纸一定是对的，老师一定是对的，人要有质疑精神，不过要实事求是。孩子还小，我觉得要教给他们挑战权威的能力。至于那一位孩子，我也找他个别谈了话，老师没讲过1-2=0，你不能自己编，讲话要实事求是。孩子就像一棵小树，小树长歪了，我们有义务把他扶正。扶正的小树才可能长成一棵参天大树。

不打压孩子提问的积极性，即使提错了，也要小心呵护这种可贵的精神。我们要努力为孩子们营造一个提问的自由空间。“有容乃大”，宽松的气氛能激发孩子求知的欲望和探索真理的动力。

二、指导提问方法

提问能力与生俱来，孩子们会随心所欲地提出千奇百怪的问题，但要从数学的角度发现问题、提出问题，还需要引导。教师要依据低年级孩子的年龄特点和认知特点，设计一些学生熟悉的生活情境，指导学生“问什么”“怎么问”。

（一）模仿起步

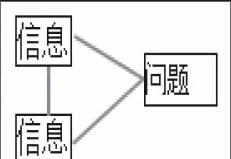
数学是思维的体操，语言是思维的外衣，培养学生的语言表达能力是促进学生思维能力发展和学好数学的有效途径。正如数学教育家斯托利亚尔所说：“数学教学也就是数学语言的教学。”刚入学的孩子，一般会有一些模糊的数的认识，数学语言的积累几乎为零，缺乏语言组织能力，提出的数学问题缺乏逻辑性。教师要尽快帮助学生不断地积累起数学语言，学会正确地表达，并且要避免啰唆重复。儿童具有很强的模仿能力，学习的第一步就是模仿，即教师说学生跟。如一年级上册学习加法的第一课，教师指导看懂图意后，可以把规范的三句话板书在黑板上，“马戏团的小丑有红气球3个，绿气球1个，他一共有几个气球？”带着学生说几遍，并告诉学生，把一件事一个数量明确告诉对方的叫信息，问别人的一句话叫问题。学生数学语言的积累就从模仿起步了。

这第一步要是教师带着走的，教师的言行对学生有着潜移默化的影响，起步阶段教师语言一定要规范，要明确，要言简意赅。通过看图说话来丰富学生的数学语言是一种非常有效的练习方法。每次练习时，教师不要满足于学生会列式就行了，而应该创造机会多让学生看着图说三句话，以此来培养学生用规范的数学语言来表达的能力。

（二）逐步积累

有些学生一时半会儿不会提问，我们教师不要操之过急，多带着学生练习几次，学生慢慢就能自己领悟了。先要学会找问号，问号在大括号下，可提求总数的问题；问号在其中一部分处，可提求部分数的问题，这就是学习积累的过程。像“总数”“部分数”这些术语都可以告诉学生，他们能理解，也便于表达。就这样，学生先是看到问号就知道该问什么，慢慢过渡到能根据内在的数量关系来发现问题，提出问题。他们逐步能体会到两条相关的信息可以提出一个相关的问题，在脑中逐渐建立起这样的模型。

有些题图上的结果一目了然，直接能看到，有些学生会搞不懂，为什么结果知道了还要问。这种练习，可以选择结果不明确的，如，右手的棋子遮住了，看不到。这种结果看不到的题目学生更能体会到问题的实质性，不知道，所以问，避免结果能直观看到而不会问的情况。我们还可以从图画题过渡到图文结合题，如妈妈买了10个苹果 ，吃了3个， 抽象的数摆在那儿，学生不可能去数，只能依据内在的数量关系来推理提问。

（三）搭设台阶

小学低年级学生的知识基础和生活经验相对比较欠缺，也不具备很强学习能力，其思维一般处于以具体形象思维为主的阶段。动手操作有助于开发右脑，促进左右脑的协调发展。动手操作能使抽象的问题具体化，学生借助操作这一思维的“脚手架”，有助于在大量感性材料的基础上激活思维，使认识从形象上升到抽象，深化对知识的理解。学习求总数和求剩余的基本数量关系时，我们可以让学生动手操作，利用学具在桌上摆，如有5个苹果，拿走3个，可以提出什么问题呢？基于亲身实践，学生往往有话可说。条件不具备时，也可以辅助以动态的课件演示或者老师的手势演示。比如，老师的左手有3支笔，右手有2支笔，然后老师演示把两只手的笔合起来，这时，学生自然就能发现并提问了。

三、提升问题质量

学生的提问能力其实是一种心理素质、生活经验、知识积累和语言技能的综合能力。要提高学生提问的质量，还需要在一定的情境中进行思维训练。

（一）创设情境

教师只有主动为学生创造提出问题的条件，才能提高学生从数学角度提出问题的能力。每次新学一个内容，都可以鼓励学生先大胆提出问题。如学习认识时间之前。可以让学生说说你想了解时间的什么知识？根据学生们提出的问题，我们可以分成数学问题和非数学问题，数学问题中哪些是这节课可以解决的，哪些等以后学了才能解决。

课本里有很多主题图，虽然没有提问要求，但我们可以引导学生们看图提问。比如一年级下册P8第二单元20以内退位减法主题图，画面呈现的是游乐场的情境，有两条信息是没有问题出现的，“小雪说，我套中了7个；小华说，我套中了12个。”这是一个很好的资源，可以引导学生提出不同问题。这个有意设计的提问环节，在我班引发了一场热烈的讨论。生一说，两人共套中几个；生二说，小雪比小华少套中几个；生三说，小雪再套几个就和小华同样多了；生四说，小雪再套几个就可以超过小华了；生五说，小华给几个小雪，两人就同样多了？生五话音刚落，就有心急的生六跳出来说，谁套的就是谁的，不能给对方，不然比赛就不好玩了。看来，孩子们的提问潜力是相当大的，只要用心开发，就能异彩纷呈。衍生出的题外话是生活中的常识，我们的数学是为生活服务的，生六的话言之有理，教师要给予肯定。但不能否定的是这个问题还是好问题，在时间允许的情况下，可以让学生展开讨论，两人的个数可能同样多吗，什么情况下可以一样多。

（二）多维思考

由于同一类型的题目解多了，学生的大脑中就会形成一种固定的思维模式。如河里有48只鸭子，第一次游走了20只，第二次游走了8只，两次一共游走多少只？很多孩子想都没想，就列式为48-20-8=，其实内心根本就没分析过数量关系，题目要求什么没注意，想当然就匆忙列式了。为了防止思维定式，我们可以设计一题多问的练习，先不出现问题，而是让学生来提问。学生的思维可活跃了，有的问还剩几只，有的问两次共游走几只？还有的问第一次游走后还剩几只？第一次比第二次多游走几只？这样的训练能开拓学生的思维，把关注点放在问题上，也能帮学生厘清内在的数量关系。这是训练学生开放式思维的好方法。

（三）反找信息

我们指导学生发现问题，提出问题是顺向思维，如果能让学生从问题想起，就是反向思维。平时练习一下有助于培养思维的灵活性，使学生的思路更通畅。一年级的教材中已经出现了有多条信息，需要根据问题来选用相应信息的题目。如“灰兔拔了8个萝卜，白兔拔了9个萝卜，灰兔比白兔少拔几个萝卜？”很多孩子往往只看一半就匆忙下笔8+9=17（个），其实根本没有看完题目。解决这一类题，我们可以使用分析法，从问题出发，引导学生思考问题是什么？要求灰兔比白兔多拔几个要知道什么信息？学生很快就能说出灰兔拔的个数和白兔拔的个数，按图索骥，找到相应的信息，问题就迎刃而解了。像这样的分析法虽然是为了解决问题，逆向思维，但这样的练习能促使学生重视问题，能按需选择信息。结束后，可以问问图中所列算式“8+9=17”表示什么？这个算式回答的是什么问题？如此练习，使学生的思维更缜密。

逆向思维训练还可以采用这种形式，补充条件。如“ ，二班有40人，二班比一班多几人？”学生会自觉地从问题想起，根据内在的数量关系来补充相应条件。

提问水平的高低与思维水平相辅相成，高水平思维才能提出高质量的问题。由于低年级孩子的思维能力处于“待开发”阶段，教师要精心选择学习素材，设计学生活动，引导学生充分经历观察、操作、思考等活动，使学生思维的灵活性、深刻性、发散性这些特质得到进一步开发。思维发展了，提问的质量就高了。

人教版实验教材六年级语文课本中有一篇课文是《真理诞生于一百个问号之后》，文中讲到“那些定理、定律、学说的发现者，差不多都善于从细小的司空见惯的现象中看出问题，不断解决疑问，追根求源，最后把‘？拉直变成‘！，找到了真理。”我们的数学也是这样，我们要培养学生的问题意识，让学生学会发现，敢于提问，学会提问，善于提问，在提问中不断地获取新知，成为一名创新性人才。