基于FLUENT的内孤立波质量源造波方法*
姜 海 郭海燕 张 林 王 伟
(中国海洋大学工程学院 青岛 266100)
海洋内波是指在海水稳定层化的海洋中产生的、最大振幅出现在海洋内部的波动。海洋内波的产生应具备两个条件: 一是海水密度稳定分层, 二是要有扰动能源, 缺一不可。由于海水的密度分布经常处于不均匀状态, 因此海洋内波是一种比较普遍的现象(杜涛等, 2001; 柯自明等, 2009; Xu et al, 2012)。其中,内孤立波是一种强非线性的潮成内波, 非线性与色散效应的平衡使得其在传播过程中可以保持稳定的波形和不变的速度(方欣华等, 2005)。内孤立波通常具有很大的振幅和波长, 在传播过程中携带有巨大的能量, 对海洋结构物构成很大的威胁(Roberts,1975; Osborne et al, 1980; 张波等, 1998)。
现在广泛使用的内孤立波理论有 KdV理论、mKdV理论、eKdV理论及MCC理论等(Michallet et al,1998; Choi et al, 1996, 1999; Helfrich et al, 2006)。近些年来, 随着计算机技术及计算流体力学的发展, 采用计算流体力学(CFD)的方法研究内孤立波的生成传播及其与结构物的相互作用, 已成为重要的研究方法之一。内孤立波数值模拟常用的方法有两类——仿物理造波法和纯数值造波法。仿物理造波法包括平板拍击法、双推板法、摇板法等, 纯数值造波法包括速度入口法和源项造波法。付东明等(2009)结合KdV理论发展了双推板数值造波方法; 陈钰等(2009)基于KdV理论, 采用速度入口法, 建立了可有效模拟弱非线性海洋内孤立波的二维分层数值水槽; 高原雪等(2012)基于MCC理论, 采用速度入口法, 建立二维内孤立波数值水槽, 实现了振幅可控的内孤立波数值模拟; 李水娟等(2012)基于KdV理论, 采用速度入口法建立了三维内孤立波分层数值水槽; 王旭等(2014)结合 eKdV理论,从理想流体完全非线性欧拉方程出发, 发展了内孤立波质量源数值造波方法, 所得结果跟理论与实验吻合较好; 王伟等(2016)基于 KdV、mKdV理论, 采用平板拍击法进行内孤立波数值模拟,并详细分析了内孤立波波致流场变化。
自从 Brorsen等(1987)基于“水下爆炸”原理, 首次提出基于势流理论的适合于边界积分方程法的质量源函数造波方法后, 质量源方法已被广泛应用于表面波数值模拟(Lin et al, 1999; 刘秀丽等, 2015; 周玲玲等, 2015), 但目前采用质量源法模拟内孤立波的论文很少。王旭等(2014)采用线源形式的质量源, 结合eKdV理论成功模拟了内孤立波。本文采用两个点源形式的质量源, 基于FLUENT软件, 从黏性不可压缩流体的Navier-Stokes方程出发, 结合KdV、eKdV理论建立有限水深两层流体中的内孤立波质量源数值模拟方法, 并将所得结果与理论和实验相对比, 验证方法的可行性。
1 数学模型
1.1 造波方法
流体力学中的源方法是在流体力学控制方程中加入特定的源项, 以此激发产生所需要的流场。源项是一个广义量, 它代表了那些不能包括到控制方程的非稳态项、对流项与扩散项中的所有其它各项之和,包括质量源项、动量源项、能量源项和湍流源项。其中, 质量源方法是在连续性方程中加入附加质量源项, 通过对附加质量源项进行特定的设置, 以此来产生目标流场。Brorsen等(1987)对质量源方法进行了详细的数学物理推导, Kim等(2010)从雷诺输运定理出发, 详细推导了质量源表达式。
本文用质量源法建立二维内孤立波数值水槽,如图1所示。上层流体的深度为h1, 密度为ρ1, 下层流体的深度为h2, 密度为ρ2, 建立如图1中所示的坐标系oxz, ox轴位于两层流体尚未扰动时的分界面上,oz轴垂直向上。在左边界处, 上下层流体中各放置一个点源形式的质量源, 上层中的源 Ω1的强度为S1( x, z, t), 下层中的源 Ω2的强度为 S2(x, z, t)。源 Ω1不断释放质量, 源 Ω2不断吸收质量, 从而产生下凹型的内孤立波。

图1 内孤立波数值水槽示意图Fig.1 Scheme of the numerical wave tank for generating internal solitary wave
在质量源区域, 加入源项后, 流体的控制方程变为如下形式:

式中, S ( x, z , t)为源强, μ为动力黏度系数。
假定质量源引起的流体质量的增减对应入射的孤立波波面的变化, 则对于源Ω1、Ω2有:

式中, C为内孤立波相速度, η( t )为内孤立波波面。
质量源为点源, 在质量源区域内均匀分布, 可认为质量源强度仅为时间 t的函数, 即 Si( x, z, t) = Si( t),则质量源Ω1、Ω2的源强的表达式如下:

式中,1A、2A分别为源Ω1、Ω2的面积。
1.2 消波方法
采用海绵层阻尼消波法(韩朋等, 2009)进行消波。该方法的原理是, 通过在特定的计算区域的动量方程中添加阻尼源项来削弱传入该区域的波动。阻尼消波的效果与消波段的长度有关, 该长度应至少为入射波波长的一倍。消波区加入阻尼源项后的动量方程为:
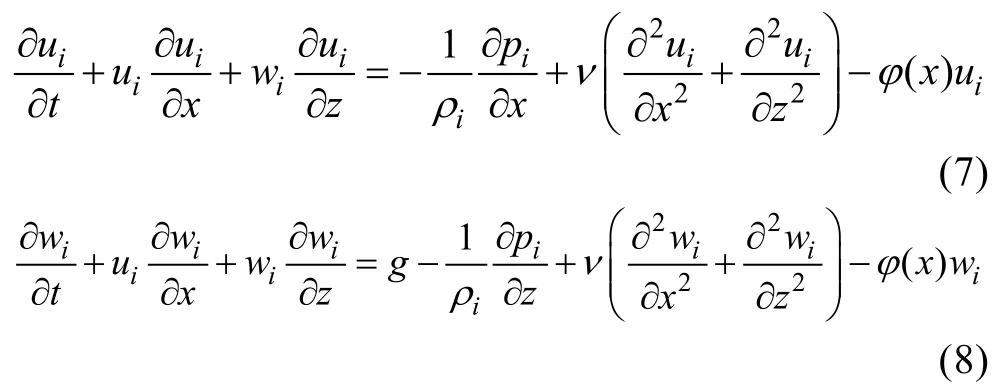
其中, ν为运动黏度系数, ()xφ为阻尼消波系数, 是在阻尼段起点为零的单调递增函数。阻尼消波系数取线性分布的形式, 如下式所示:

式中: α为阻尼系数内的经验参数,1x为海绵层的起始坐标,2x为海绵层末端坐标;sL为海绵层的长度, 在数值计算中通常取1—2倍波长。
2 内孤立波数值模拟
2.1 模型建立与网格划分
王飞(2015)在中国海洋大学物理海洋实验室, 利用密度分层水槽, 采用重力塌陷法制造不同振幅的内孤立波, 通过实验研究内孤立波的生成及流场特性。水槽长15m, 宽0.35m, 高0.7m, 额定水深0.6m。采用 Oster双缸法制取密度分层流体, 上层流体高度9.5cm, 密度1035kg/m3, 下层流体高度48.5cm, 密度1054kg/m3; 采用 PIV技术监测流场信息。为与实验结果进行对比, 本文选取上述流体参数, 以实验中得到的三个波高作为设定波高进行数值模拟。
黄文昊等(2013)通过实验, 研究了四种内孤立波理论的适用范围, 利用内孤立波的非线性参数ε和色散参数ξ来定量表征各内孤立波理论的适用区间, 结果表明:ξ<0.1,ε≤ξ时, KdV理论适用;ξ<0.1,ξ<ε<时, eKdV理论适用。以此为依据, 对三组工况分别选用适用的内孤立波理论作为数值模拟输入条件。数值模拟工况如表1所示:

表1 数值模拟工况Tab.1 Conditions of the numerical simulations
网格划分: 数值水槽采用结构化网格进行划分,x方向网格尺寸取Lx= 2 cm,z方向网格尺寸取Lz= 0 .5cm, 共 87000个网格。消波区的长度取为1—2倍波长。
源的设置: 两质量源的大小应满足点源假设, 即其高度Hs应远小于数值水槽的水深H, 宽度LΩ应远小于内孤立波的波长λ, 通常质量源宽度应小于波长的5% (Linet al, 1999; Hafsiaet al, 2009),故将源Ω1、Ω2分别放置在左边界处上、下层流体中的一个网格内。Lin等(1999)指出质量源位置距离分界面1/3层厚处模拟结果与理论最相符, 并将此位置称为“standard elevation”。故参考 Lin 等(1999)的结论, 将两源距离两层流体分界面的距离各设为相应层厚度的 1/3, 即Ω1距离两层流体分界面 3.5cm,Ω2距离分界面 16cm。从后面的模拟结果来看, 这样的设置取得了良好的效果。
2.2 FLUENT设置
边界条件: 水槽左边界设为对称边界; 水表面采用刚盖假设(方欣华, 2005), 设为固壁边界; 水底设为固壁边界; 右边界设置为压力出口。
液面追踪方法: 采用VOF方法(韩朋等, 2009)来追踪两层流体分界面处的内孤立波波面。流体体积函数F定义为单元内流体所占有的体积与该单元可容纳流体体积之比。若单元体被指定相流体占满, 则该单元F值为 1; 若单元体被另一相流体占满, 则单元的F值为0; 若单元体的F值在0与1之间, 则表示该单元为包含两相流体的交界面单元。
UDF设置: 利用 FLUENT中的 DEFINE_SOURCE宏定义上下两源的源强, 添加到 FLUENT中造波源区域的源项加载区, 嵌入到造波区控制方程中; 利用 DEFINE_PROFILE宏在压力出口边界给定计算域静水压强, 使得出口边界处水体能够自由流出, 保证计算域内压力出口附近上下层水深为定值(张齐焰, 2008; 陈钰等,2009)。
求解设置: 控制方程的对流项采用一阶迎风格式,扩散项采用中心差分格式, 压力速度耦合方式采用PISO算法, 压力插值选用体积力加权法, 两相界面的构造方法选用几何重构; 初始时水槽中流场速度取为0,时间步长设为0.01s, 每个时间步最大迭代次数20次。
3 数值造波结果及分析
3.1 质量源法中内孤立波的生成
两质量源的强度随模拟时间不断发生变化, 使得造波源附近的流场速度发生变化。图 2为工况 A中两造波源附近两个时刻的速度矢量图, 图中白线分别为数值水槽左边界和上边界, 黑色矩形分别为质量源Ω1和Ω2。从速度矢量图中可以看出, 随着源Ω1不断释放质量、源Ω2不断吸收质量, 源附近上下层流体的速度场均发生变化, 上层流体产生沿x正向的水平速度, 下层流体产生沿x负向的水平速度, 这与内孤立波波致流场中的速度趋势是相同的。
图3为 A工况造波初期四个不同时刻质量源区域附近两相界面图, 展示了造波开始后左侧边界附近两相界面的变化, 其中灰色部分为上层流体, 黑色部分为下层流体。从图中可以看出, 两层流体的界面在源Ω1不断释放质量、源Ω2不断吸收质量的驱动下,缓慢而平稳地发生下凹, 并最终形成一个完整的下凹形内孤立波。
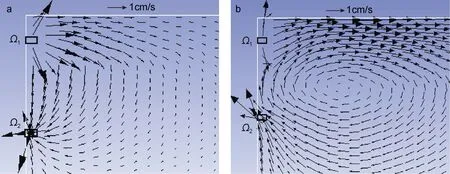
图2 质量源附近速度矢量图Fig.2 Velocity vector near the mass source

图3 质量源附近两相界面变化图Fig.3 Change at the boundary of two phases near mass source
3.2 数值造波结果及对比
图 4为三个工况下内孤立波数值模拟所得波形(CFD)与理论波形(KDV)和实验波形的对比。从图中可以看出, 三个工况下数值模拟波形均光滑对称, 且与理论及实验波形吻合良好; 各工况数值模拟所得波高分别为-3.988cm、-7.320cm和-8.092cm, 与设定波高吻合良好。从对比中可以看出, 本文所述质量源方法模拟内孤立波所得波形和波高同理论解和实验结果是一致的。

图4 数值模拟波形与理论及实验的对比Fig.4 Comparison in the results of numerical, theoretical and experimental simulations
图 5为波谷断面处波致水平流速沿垂向分布数值模拟、理论解及实验结果的对比图。从图中可以看出, 工况A中数值模拟与理论解及实验均吻合良好。工况 B、C中, 上层流体中波致水平流速较大, 致使实验监测数据失效, 但在该层数值模拟与理论解吻合较好; 在下层流体中, 数值模拟与理论解及实验均吻合较好。
图6为内孤立波波致水平流速数值模拟、理论解及实验的对比图。从对比中可以看出, 工况A中模拟峰值比理论和实验结果略小, 图像介于理论解和实验之间, 整体上与二者吻合良好; 工况 B、C中同样由于上层流体的流速较大, 超出系统的测量范围, 造成实验监测数据失真, 仍可以看出, 上层流体中数值模拟与理论解吻合良好, 下层流体中三者的吻合度均良好。
4 结论
采用两个点源形式的质量源, 分别放置于两层流体中的上下层中, 上层流体中的质量源释放流体,下层流体中的质量源吸收流体, 激发产生下凹型内孤立波。推导质量源强度表达式, 并利用商业软件FLUENT, 基于其 UDF编译功能, 以内孤立波 KdV和 eKdV理论为依据, 从不可压缩流体的 Navier-Stokes方程出发, 发展了一种内孤立波数值造波方法,并将数值模拟结果与理论及实验进行对比。结果表明:

图5 波谷断面水平流速沿垂向分布Fig.5 Profiles of horizontal velocity at trough section

图6 波致水平流速对比图Fig.6 The horizontal vector of wave-induced velocity
(1) 造波过程中, 在上层流体中的源释放质量、下层流体中的源吸收质量的驱使下, 上下层流体速度呈现出相反的情形, 使得两层流体分界面逐渐下凹, 最终形成一个不断向前传播的下凹形内孤立波。
(2) 三个工况下波形、波高及波致水平速度的数值模拟结果均与理论及实验的吻合较好, 验证了此方法的有效性, 表明本文所述质量源法能够有效模拟内孤立波的生成与传播。
(3) 该方法作为一种纯数值造波方法, 避免了动网格的使用, 计算效率高, 耗时短, 另外不需要已知速度等边界条件, 可用于研究速度边界未知的情况,如波流相互作用等。
(4) 该方法同样可以模拟上凸型内孤立波。对于上凸型内孤立波, 其波面 η ( t )始终为正, 则(5)、(6)两式中的源强表达式 S1(t)始终为负, S2(t)始终为正,表示上层流体中的源吸收质量, 下层流体中的源释放质量, 从而驱动两层流体界面发生上凸, 形成上凸型内孤立波。
实际海洋中环境复杂, 由于表面波、流以及海底地形等因素的影响, 内孤立波波形通常不如理论波形和数值模拟波形那样光滑对称(Xu et al, 2012),在以后的内孤立波数值模拟中可以考虑波流相互耦合以及复杂海底地形下的内孤立波的数值模拟, 这样得到的波形将更趋近于实际海洋中的内孤立波的波形。
方欣华, 杜 涛, 2005. 海洋内波基础和中国海内波. 青岛:中国海洋大学出版社, 101—115, 258—281
王 飞, 2015. 内孤立波作用下小尺度竖直圆柱体的水动力特性研究. 青岛: 中国海洋大学博士学位论文, 21—32
王 伟, 郭海燕, 王 飞等, 2016. 内孤立波波致流场数值模拟研究. 海洋与湖沼, 47(3): 502—508
王 旭, 林忠义, 尤云祥, 2014. 两层流体中内孤立波质量源数值造波方法. 上海交通大学学报, 48(6): 850—855
付东明, 尤云祥, 李 巍, 2009. 两层流体中内孤立波与潜体相互作用数值模拟. 海洋工程, 27(3): 38—44
刘秀丽, 段梦兰, 高 攀等, 2015. 基于 OpenFoam 的数值波浪水槽研究. 复旦学报(自然科学版), 54(3): 373—378,385
张 波, 黄长穆, 1998. 中国南海流花11-1油田的深水开发技术. 中国海上油气(工程), 10(3): 36—44
张齐焰, 2008. 非线性波浪冲击透空结构物数值模拟. 杭州:浙江大学硕士学位论文, 31—40
李水娟, 余真真, 罗龙洪等, 2012. 三维数值波浪水槽内孤立波特性分析. 水电能源科学, 30(7): 96—99
杜 涛, 吴 巍, 方欣华, 2001. 海洋内波的产生与分布. 海洋科学, 25(4): 25—28
陈 钰, 朱良生, 2009. 基于Fluent的海洋内孤立波数值水槽模拟. 海洋技术, 28(4): 72—75, 100
周玲玲, 丁全林, 兰庆琳等, 2015. 基于LB方法的质量源造波的数值波浪水槽. 水电能源科学, 33(3): 99—103
柯自明, 尹宝树, 徐振华等, 2009. 南海文昌海域内孤立波特征观测研究. 海洋与湖沼, 40(3): 269—274
高原雪, 尤云祥, 王 旭等, 2012. 基于MCC理论的内孤立波数值模拟. 海洋工程, 30(4): 29—36
黄文昊, 尤云祥, 王 旭等, 2013. 有限深两层流体中内孤立波造波实验及其理论模型. 物理学报, 62(8): 084705
韩 朋, 任 冰, 李雪临等, 2009. 基于VOF方法的不规则波数值波浪水槽的阻尼消波研究. 水道港口, 30(1): 9—13
Brorsen M, Larsen J, 1987. Source generation of nonlinear gravity waves with the boundary integral equation method.Coastal Engineering, 11(2): 93—113
Choi W, Camassa R, 1996. Weakly nonlinear internal waves in a two-fluid system. Journal of Fluid Mechanics, 313: 83—103
Choi W, Camassa R, 1999. Fully nonlinear internal waves in a two-fluid system. Journal of Fluid Mechanics, 396: 1—36
Hafsia Z, Hadj M B, Lamloumi H et al, 2009. Internal inlet for wave generation and absorption treatment. Coastal Engineering, 56(9): 951—959
Helfrich K R, Melville W K, 2006. Long nonlinear internal waves. Annual Review of Fluid Mechanics, 38: 395—425
Kim G, Lee M E, 2010. On the internal generation of waves: control volume approach. Ocean Engineering, 38(8—9): 1027—1029
Michallet H, Barthélemy E, 1998. Experimental study of interfacial solitary waves. Journal of Fluid Mechanics,366(1): 159—177
Osborne A R, Burch T L, 1980. Internal solitons in the Andaman Sea. Science, 208(4443): 451—460
Roberts J, 1975. Internal Gravity Waves in the Ocean. New York:Marcel Dekker Inc, 2—13
Xu Z H, Yin B S, Yang H W et al, 2012. Depression and elevation internal solitary waves in a two-layer fluid and their forces on cylindrical piles. Chinese Journal of Oceanology and Limnology, 30(4): 703—712

