基于BP神经网络方法的近岸数值海温预报释用技术*
匡晓迪 王兆毅 张苗茵 何恩业 邓小花
(国家海洋环境预报中心 北京 100086)
随着数值预报和同化技术的快速发展, 从全球到近岸的不同水平分辨率、不同动力过程、不同预报精度的海洋数值预报模型不断被建立, 并具备一定的精度(李冬等, 2004; 张权等, 2011; 李云等, 2011;方长芳等, 2013; 魏泽勋等, 2015; 王辉, 2016)。然而,区域海洋数值预报受地形精度、物理过程描述及近岸观测数据等因素的限制, 在近岸和浅水区预报表现受到制约, 对定点海温预报准确度不高。对于有观测资料的站点, 定点数值预报与观测的结合大多只通过人工经验判定, 往往不能同时满足稳定的预报表现和客观计算两方面的需求。因此对近岸海温预报来说, 数值预报的结果不能直接作为预报产品进行发布。
预报释用技术是数值预报和预报产品发布之间的桥梁。该技术可以充分挖掘数值预报产品中的有用信息, 进一步提高其精度, 实现预报产品的覆盖率、客观性和准确性的同步提升, 突出预报产品的客观解释应用特征, 使其具有优良的服务体验、更好的适用性和更高的准确性。这些释用技术基本上可以归纳为两大类: 一类是以人的经验为主的方法(严明良,2004; 堵盘军等, 2013); 另一类是客观定量方法, 如动力释用方法(苗世光等, 2009; 胡波等, 2014)、统计释用方法(程戴晖等, 2001; 张宏秋等, 2004; 胡春梅等, 2006; 李江萍等, 2008; 曾瑾瑜等, 2015)等。
人工神经网络方法是统计释用方法中一种非线性拟合方法。该方法是人脑及其活动的一个理论化的数学模型, 是一个大规模的非线性自适应系统(蒋宗礼, 2002)。近些年, 人工神经网络在海洋预报中得到广泛运用, 水位(Filippo et al, 2012)、盐度(张文孝等,2006)、海浪(齐义泉等, 2005; 王华等, 2007;Deshmukh et al, 2016)、风暴潮(Tissot et al, 2002) 、赤潮(黄良民等, 1994; 吴京洪等, 2001; 杨建强等,2003; 何恩业等, 2008)、潮汐(王建华等, 2007; 欧素英等, 2008)、海冰(卢海, 2007)等预报及气候预测(张韧等, 2000; 王业宏等, 2003; 周林等, 2009; Liu et al,2016)和垂直结构计算(刘辉等, 2008; Chaudhari et al,2008; Zhao et al, 2015)等领域已有初步应用。Vilibić等(2016)采用自组织映射网络, 基于地波雷达和气象数值预报建立了实时海流预报系统, 通过与主流区域海洋模式 ROMS比较, 认为神经网络方法建立的模型与基于海洋动力方程建立的模型精度相当甚至略优, 给基于人工智能的近岸海洋要素定量预报开辟了新的思路。对于近岸定点海温的定量预报, 由于近岸海洋是强非线性复杂系统, 地域和基础数据依赖性明显, 使得数值预报具有较大的不确定性, 因此预报一般采用经验方法或者分型统计方法(张宏秋等,2004), 采用神经网络方法尚无前例。基于人工神经网络的误差后传算法(back-propagation neural network,简称BP)是人工神经网络中应用最为广泛的一种多层前馈网络的学习算法, 它可以通过神经网络的自学习功能, 确定神经元之间的耦合权值, 从而使网络整体具有近似函数的功能, 非常适用于非线性系统的建模研究(张宏秋等, 2004)。在理论上, BP模型能高精度逼近任意复杂系统, 可有效用于常规方法不易处理的关系辨识和复杂预测, 并为建立合理、可靠和准确的预报模型提供依据(Vilibić et al, 2016)。对于确定的海洋要素, 通过不同的因子场得到多个典型因子,进而通过BP神经网络实现典型因子场与海洋要素之间的非线性建模, 在海洋预报中也有成功提高预报精度的实例(齐义泉等, 2005; 何恩业等, 2008; Tisso et al, 2014; Deshmukh et al, 2016)。本文以提高数值预报的近岸精细化预报精度为目的, 将近岸台站的定点表层海温作为预报对象, 开展基于 BP神经网络的预报释用技术研究, 旨在解决海温数值预报产品在近岸、单点预报误差大的问题, 有针对性地提高数值海温的预报精度和质量。第一节介绍预报释用建模使用的数值预报及观测数据, 简述了BP神经网络方法的基本结构、算法和比测实验方案; 第二节基于各组调训实验的误差分析, 研究了固定影响因子和一般影响因子的作用和权重, 分析了释用模型对预报精度的提升效果, 开展预报检验, 并与人工经验预报误差进行了比较, 筛选出了最佳预报模型。
1 数据和方法
1.1 研究数据
1.1.1 气象预报数据 数值气象资料为国家海洋环境预报中心的 WRF风场预报网格资料, 调训模型数据时间范围为2014年1月1日至12月31日, 预报实验数据时间长度为2015年1月1日至4月30日。每天 8、14、20时 3时次(北京时)进行平均, 共 365个样本, 网格精度为 1/12°×1/12°, 利用双线性插值,将数据插值到台站所在位置。具体气象要素选取了海面 2米比湿(Q2)、海面气压(SLP)、净热通量(SWDOWN)、海面2米气温(T2), 纬向10米风速(U10)、经向10米风速(V10)、10米风速大小(VEL)7个要素。1.1.2 台站观测数据 台站观测的主要观测要素涵盖潮汐、表层水温、表层盐度、海浪、风向、风速、气压、气温、相对湿度、能见度和降水量等。台站依据《海滨观测规范》、《地面气象观测规范》和《海洋自动化观测通用技术要求》等观测工作执行标准, 开展各观测项目和要素的数据采集处理、传输, 其观测资料能在一定程度上反映出观测海区环境的基本特征和变化规律。本文使用舟山站的常规台站观测资料中的海温和气温数据, 分别作为预报因子(调训和预报)和检验数据使用。调训使用的观测资料时间长度为2014年1月1日至12月31日, 预报实验使用的观测资料时间长度为2015年1月1日至4月30日。每天8、14、20时3个时次(北京时)进行平均, 共365个样本, 观测要素和具体影响要素选取了观测气温(Tao)和表层海温(Tso)。
1.1.3 海温预报数据 数值海温采用国家海洋环境预报中心开发的全球业务化海洋学系统(Chinese Global Ocean Forecasting System, CGOFS), 调训模型数据时间长度为2014年1月1日至12月31日, 预报实验数据时间长度为2015年1月1日至4月30日。释用采用每天20时(北京时)的数值模拟海温场, 共365个样本, 检验采用每天8、14、20时3个时次(北京时)进行平均, 网格精度为 1°/30×1°/30, 选取离站点最近的模式水点代表台站的海温数值模拟结果, 并计算了位置误差。
1.1.4 经验预报 采用2014年全年时效为24小时的日平均海温经验预报值的时间序列和台站观测海温对比, 并采用与释用预报相同方法进行误差分析,与释用预报的结果进行对比。
1.2 人工神经网络方法
BP网络是一种非线性映射人工神经网络, 具有很强的学习和记忆能力, 一般由一个输入层、若干隐含层和一个输出层组成。它是一种有导师的学习算法,通常是应用最速下降法来调整各层权值, 并最终达到预先给定的误差为止。本文采用单隐层BP网络建立非线性回归模型, 隐层神经元采用S型对数激活函数(单极性 Sigmoid函数), 输出层神经元采用线性激活函数, 为了有利于使网络联接权加快脱离误差曲面的平坦区, 引进动量项。
1.2.1 BP网络结构模型
单隐层BP网络结构如图1所示, 共分3层:
第1层为变量输入层, xj, j=1, 2, …n0为输入变量,n0为输入变量的个数。若设x0为第一隐层中激活函数的域值, 则输入向量总共为 n0+1维。x0一般取为-1,将其增广到输入量中, 作为一个分量, 则有
第2层为隐层, 设有n1个神经元, 则其输出向量为g=(g0, g1, g2, …,1ng ), 其中g0为第一隐层中激活函数的域值, 一般取为-1。
第3层为输出层, 设有m个神经元, 网络的输出向量为y=(y0,y1,y2,…, ym) 。

图1 单隐层BP网络结构Fig.1 Structure of single-hidden-layer BP network
隐层神经元采用 S型对数激活函数(单极性Sigmoid函数), 输出层神经元采用线性激活函数。S型对数激活函数表达式为:

隐层输出向量为:

输出层输出向量为:
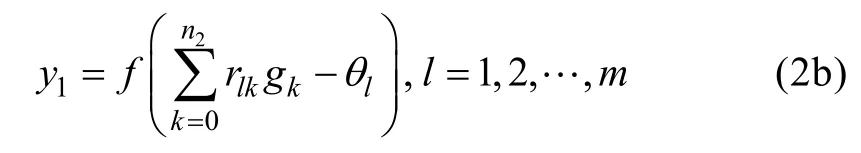
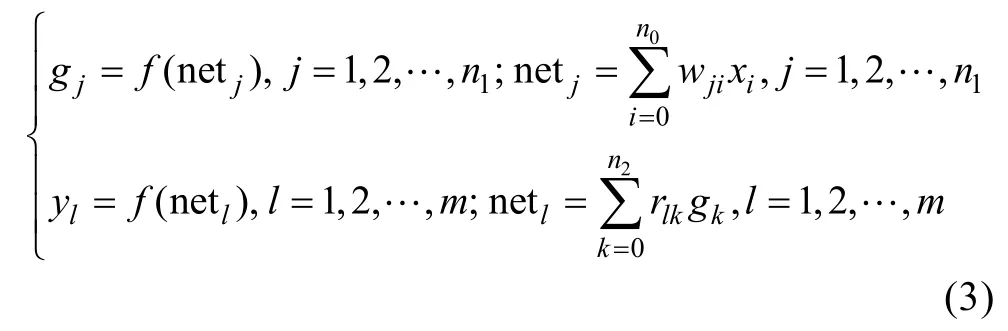
1.2.2 BP网络权值的动态学习算法 设一共有α个样本对, 第 p个样本对(pptx, )输入模式后输出方差为:
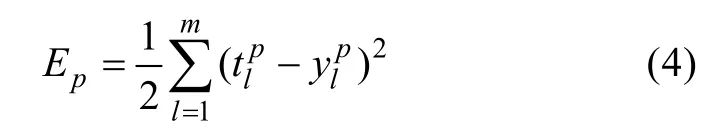
α个样本对经正向传播运算后网络总误差为:

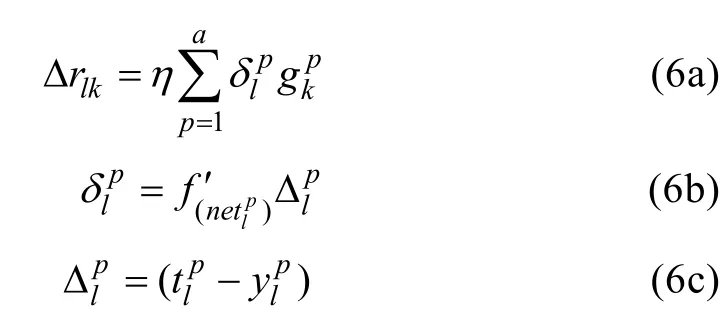
输入层到隐层的联接权修正量为:

设n为迭代次数, 应用梯度法可以得到网络各层联接权的迭代关系为:

为了有利于使网络联接权加快脱离误差曲面的平坦区, 引进动量项mcΔwuv, 则以上方程组变为:
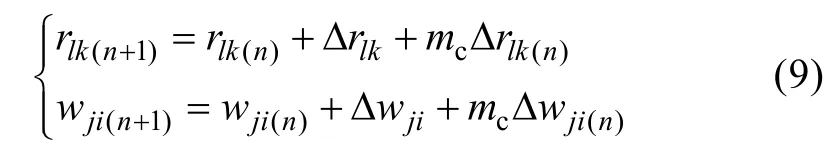
上面各式中, η表示学习率, 其值通常在0.01— 1.0之间。学习率η选得太小, 会导致网络参数(耦合权值)修改量过小, 收敛缓慢; 选得太大, 虽然可以加快学习速度, 但可能致使权值修改量在稳定点附近持续振荡, 难以收敛, mc为动量因子, 一般取0.9左右。动量项的作用在于记忆前一时刻联接权值的变化方向(即变化量的值), 增加动量项, 利用其“惯性效应”来抑制可能产生的振荡, 起到平滑作用, 这样可以采用较大的学习率η, 以提高学习速度。本文调训模型目标函数误差为0.005, 学习率0.2, 动量因子取0.9。
1.2.3 集合样本的构造 由于研究使用的各数据单位不一致, 对 BP建模效果存在较大影响, 在影响因子的样本序列输入神经网络前, 需要对集合样本进行去量纲化、归一化和类间交叉处理; 本文使用的去量纲化和归一化计算方法为:

其中X为集合样本, Xmin为样本最小值, Xmax为样本最大值, σX为样本方差, x为去量纲化和归一化后的集合样本。同时, 如果给定的样本要素随着时间有整体变化趋势, 不利于模型的泛化, 因此样本的组织要注意将不同类别的样本交叉输入, 对样本的类间交叉预处理, 本文采用随机数方法对集合样本进行打乱。
调训样本为2014年1月1日至12月31日共365个样本, 预报样本为2015年1月1日至4月30共120个样本。其中由于观测数据具有滞后性, 在构建观测海温和气温样本时, 以第T-1日的观测数据和第T日的数值预报构建样本集合。
在BP神经网络计算结束输出结果后, 进行反算恢复样本量纲、量级和原有序列。
1.2.4 计算步骤 单隐层BP网络反传学习算法的实现分为5步:
(1) 初始化。设置网络各联接权值(包括阈值), 置所有可调参数(权和阈值)为均匀分布的较小随机数,使每个神经元的净输入值较小, 以保证工作在激活函数变化较灵敏的区域。
(2) 信息正向传递过程的计算。输入学习样本对(xP, tP), 对每个输入样本计算各神经元的输出值。
(3) 误差反向传播。从输出层至输入层, 反向依次计算各神经元的等效误差, 然后返回步骤(2)对其他学习样本对进行正向传播计算和误差反向传播,一直到所有α个学习样本对都进行类似的运算为止。
(4) 调整各层的联接权值。按照权值调整公式,修改各层的联接权值。
(5) 返回步骤(2), 根据新的联接权值, 进行正向计算。若对每一个学习样本对(xP, tP),和输出层的每一个神经元l均满足精度要求, 即:

1.3 研究方案
本文选用舟山站为例进行预报因子的敏感性试验、调训和预报模型建模。首先将影响因子分为固定因子(数值和观测海温, 共2个)和一般因子(数值气象7个因子和观测气温1个因子, 共8个)两类, 设计4组敏感性试验: 控制实验组 NONE(无固定影响因子)、数值海温组TM(数值海温为固定影响因子)、观测海温组 TO(观测海温为固定影响因子)、数值及观测海温组TMTO(两者均作为固定的影响因子)进行模型调训。每组调训实验中, 将一般影响因子按 5—8个因子数进行排列组合后, 加上各组的固定影响因子, 共设计了 93组影响因子, 按照调训模型的误差(如无特别说明, 指均方根误差, 下同)分析进行排序, 并比较不同实验组相同一般影响因子实验之间的误差。
(1) 组1: 控制实验组NONE(93组):
实验数据: 第T日数值气象+第T-1日的台站气温观测
气象变量: Q2, SLP, SWDOWN, T2, U10, V10,VEL(比湿, 海面气压, 净热通量, 气温, 纬向、经向风速, 风速)
台站观测: Tao(气温, 下同)
(2) 组2: 数值海温组TM(93组)
实验数据: 第T日数值气象+第T-1日的台站气温观测+海温数值预报
气象变量: Q2, SLP, SWDOWN, T2, U10, V10, VEL;
台站观测: Tao;
模型数据: Tm(数值海温)
(3) 组3: 观测海温组TO(93组)
实验数据: 第T日数值气象+第T-1日的台站气温观测+第T-1日台站海温观测
气象变量: Q2, SLP, SWDOWN, T2, U10, V10, VEL;
台站观测: Tao, Tso(观测海温, 下同);
(4) 组4: 数值及观测海温组TMTO(93组)
实验数据: 第T日数值气象+海温+第T-1日的台站气温+第T-1日台站海温观测;
气象变量: Q2, SLP, SWDOWN, T2, U10, V10, VEL;
台站观测: Tao, Tso;
模型数据:Tm。
通过分析4种释用方案各93组配置实验的误差,计算了372个实验的绝对误差、平均误差、平均绝对误差和均方根误差。对4个释用方案的相同配置实验进行平行比较, 对同一释用方案下的不同配置实验也进行误差对比, 分析数值海温、观测海温在建模中的影响和作用, 比较其他影响因子的权重, 并筛选误差较小、稳定性较好的调训模型进行24小时海温预报实验, 同时以释用结果与 24小时的经验预报结果的对比结果作为参考, 选定预报释用试行方案。
2 调训实验
2.1 固定影响因子的作用
首先, 对4个释用方案进行整体误差比较, 其中NONE组误差较大且分散, 按照NONE、TM、TO、TMTO的顺序, 误差依次减小且逐步稳定, NONE为1.1°C, 且有显著高误差值出现, 有1组实验最大误差高达28°C以上, 其他3个方案均无此现象发生; TM误差低于NONE, 为0.9°C, 另外2组误差接近且都低于TM; TMTO误差略低于TO, 且整体误差均稳定的处在较低水平, TO误差为0.8°C, TMTO误差最小, 为0.7°C(表 1)。
通过误差分布可以看出(图 2), 数值海温和观测海温分别作为固定影响因子, 使得实验误差从 1.1°C分别降至 0.9°C和 0.8°C, 对降低模型误差起到了十分重要的作用; 同时, 观测海温作为固定影响因子,起到了稳定模型误差的作用, 不同配置实验之间误差的差别明显缩小。因此, 数值海温和观测海温作为固定影响因子, 可以使释用模型表现优良且稳定, 因此, TMTO方案应作为首选的释用方案。

图2 释用方案均方差分布Fig.2 Mean square error distribution of the four interpretation plans

表1 释用方案实验误差比较(单位: °C)Tab.1 Comparison in the errors among the four plans(°C)
2.2 一般影响因子权重分析
对 TMTO93组配置实验的误差进行排序, 对误差最低的10个实验组进行影响因子分析, 记录前10位的实验中, 对每个一般影响因子出现的频次计数,可以看出 8个一般影响因子在释用模型中的地位和权重(见表2)。总体上, 海面气温(T2)、观测气温(Tao)和海表面气压(SLP)的出现频次较高; TMTO方案中,净热通量(SWDOWN)、海面风速(VEL)和海面气压(SLP)权重较大。
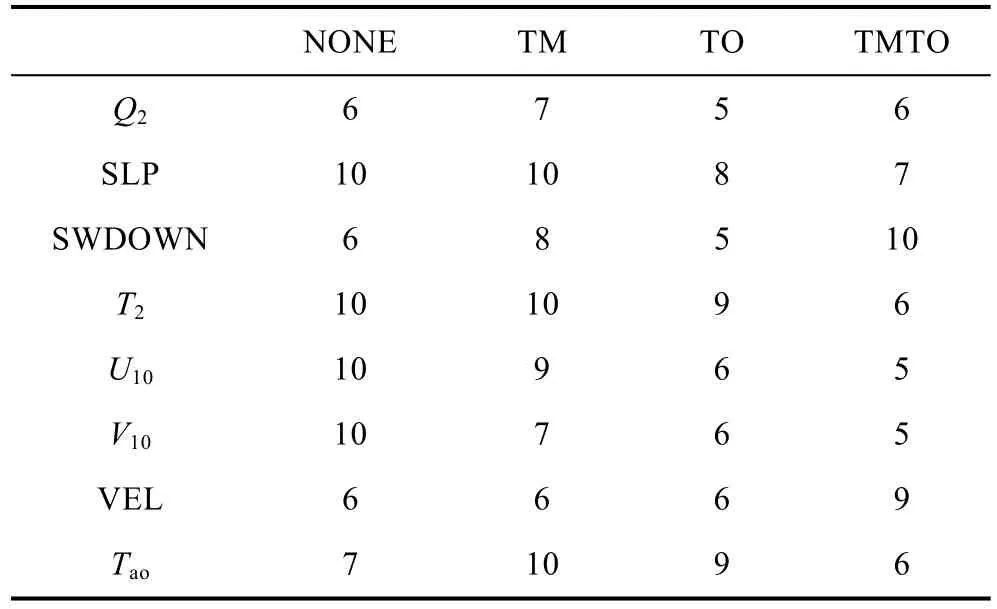
表2 影响因子在误差最小的前十组实验中出现频次Tab.2 Occurency number of affectors in the best ten combinations
2.3 预报释用与数值预报
数值预报本身存在较多的影响因素, 因此单点的海温预报误差一般不能保证, 且模式在近岸的台站附近预报能力十分有限。如图 3a所示, 数值预报的海温能够较好地表现海温的季节变化, 但预报误差较大, 均方差约为 2.2°C; 释用模型对海温的改善是明显的, TM方案将预报误差大幅减低至1.2°C, 且整体变化曲线与观测值十分接近; TMTO方案则进一步降低了误差, 提升了在海温突变时的表现, 两条曲线的变化趋势和量值都十分接近, 将图3c和a相比可以看出, 释用技术大大改善了数值海温的预报表现,提升了数值预报产品在指定区域或站点的预报准确性, 拓展了数值海温产品的应用前景。
2.4 预报释用与经验预报
对同一时段的经验预报进行误差分析(图 4, 剔除了两次海温异常峰值)发现, 经验预报总体误差较小; 但如果天气导致了短期内海温显著变化, 经验预报 1—2天的预报表现会较差, 经验预报的总体方差约为 0.6°C, 最大误差也可达 4°C以上。而释用模型可以较好地体现海温的突出变化(图3c), 总体误差约为 0.7°C, 且误差水平比较稳定, 很少有误差极大值出现, 因此经验预报与数值释用水平基本持平。
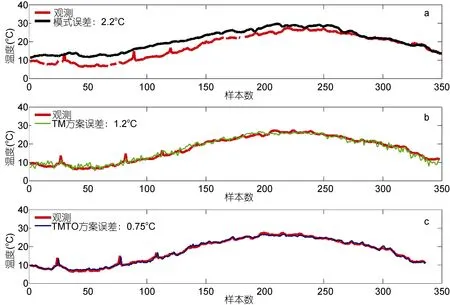
图3 观测、数值和释用海温比较Fig.3 Comparison in the results of observation, numerical modeling, and interpretation
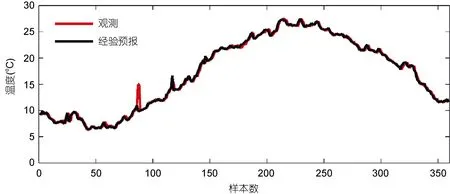
图4 经验预报与观测值的比较Fig.4 Comparison between empirical forecast and observation on temperature
3 预报实验
鉴于TMTO的93组实验的模型调训误差都相差较小(前 10位误差如表 3, 影响因子作为配置实验名称), 进行预报实验时, 对每个模型都进行预报实验及误差分析, 检验模型的预报表现。基于 2015年1—5月的风场、数值海温和台站观测数据进行了为期五个月的释用试预报, 调训误差和预报误差比较如图5所示。
从图上可以看出, 各个模型的调训误差相对稳定, 预报误差比调训误差略高, 最小预报误差为0.88°C, 虽然模型之间的调训误差差别不大(表 3),但从模型的预报表现来看, 预报误差水平差别较为明显。
结合调训和预报实验结果来看, 可以选择预报误差最小的Q2SWDOWNT2V10Tao模型作为舟山站的海温释用模型, 该模型因子包含 TMTO中权重最大的短波辐射和海表气温, 两者皆与海面感热交换关系密切; 同时, 模型包含权重较大的观测气温和比湿,比湿能够影响海表蒸发过程, 从而影响海面的潜热交换; 另外, 考虑到舟山站的地理位置, 纬向风(南风或北风)除了影响海表失热过程, 还可以通过平流输运带来暖湿或干冷的空气, 间接影响表层海温,因此该影响因子的配置对舟山站的表层海温均合理有效。

表3 TMTO组前10位模型配置及误差(单位: °C)Tab 3 Training errors of the best 10 combinations in plan TMTO

图5 配置实验的调训误差(红)和预报误差(蓝)Fig.5 Training errors (red) and forecast errors (blue)
4 结论和展望
本文以海温为突破口, 以舟山站为示范, 开展了定点数值海温预报释用技术研究, 在数值预报和预报产品之间建立桥梁, 客观地提高定点海温预报精度, 形成了如下结论:
(1) 基于 BP人工神经网络的预报释用技术,可以大幅降低近岸数值预报的误差, 且不依赖主观经验;
(2) 数值海温和观测海温具有降低和稳定调训误差的作用, 是近岸数值海温预报释用不可忽略的重要影响因子;
(3) 通过学习算法, BP神经网络预报误差略高于调训误差, 但仍保持在合理水平, 与经验预报的预报能力持平;
(4) 舟山站表层海温释用的影响因子应包含短波辐射通量、气温、比湿和纬向风, 通过这些因子建立的释用模型的预报误差约为0.88°C。
通过本文的研究可以看出, 基于人工神经网络的预报释用技术确实可以充分挖掘数值系统和观测网络中的重要信息, 同步提高预报产品的客观性和准确性, 突出预报产品的客观解释应用特征, 提供具有优良服务体验、更好适用性和更高准确性的定点海温预报产品, 具有十分广阔的拓展空间和应用前景;同时, 结合海洋基本原理和物理背景的预报因子的优选和模型调训, 以及单点预报模型在区域预报产品中的适用性等, 仍将是这一工作继续深化提升的难点和重点。
王 华, 姚圣康, 珣龚茂等, 2007. 东海区域灾害性海浪长期预测方法研究. 海洋通报, 26(5): 35—42
王业宏, 金 龙, 2003. 基于自然正交展开的神经网络长期预报模型. 自然灾害学报, 12(2): 127—132
王建华, 于红兵, 宋运法等, 2007. 人工神经网络在潮汐数值预报中的应用. 海洋预报, 24(2): 47—51
王 辉, 2016. 全球海洋环境数值预报关键技术系统集成研究及应用. 中国科技成果, 17(3): 18—19
方长芳, 张 翔, 尹建平等, 2013. 21世纪初海洋预报系统发展现状和趋势. 海洋预报, 30(4): 93—102
卢 海, 2007. 基于人工神经网络的冰情预测研究. 天津: 天津大学硕士学位论文
刘 辉, 王 静, 2008. 人工神经网络方法估算海洋上混合层深度的初步研究. 热带海洋学报, 27(3): 9—13
齐义泉, 张志旭, 李志伟等, 2005. 人工神经网络在海浪数值预报中的应用. 水科学进展, 16(1): 32—35
严明良, 2004. 数值产品释用方法在预报业务系统中的应用.推进气象科技创新加快气象事业发展——中国气象学2004年年会讨论文集. 北京: 中国气象协会
李 云, 万莉颖, 刘钦政, 2011. 卫星高度计资料在三维海温和盐度数值预报中的应用. 海洋学报, 33(6): 64—72
李 冬, 刘克修, 韩桂军, 2004. 变分伴随数据同化方法在断面海温数值计算中的应用研究. 海洋通报, 23(4): 1—8
李江萍, 王式功, 2008. 统计降尺度法在数值预报产品释用中的应用. 气象, 34(6): 41—45
杨建强, 罗先香, 丁德文等, 2003. 赤潮预测的人工神经网络方法初步研究. 海洋科学进展, 21(3): 318—324
吴京洪, 杨秀环, 唐宝英等, 2001. 大亚湾澳头增养殖区赤潮与环境的关系研究 I. 浮游植物总生物量与环境因子的关系. 中山大学学报(自然科学版), 40(3): 37—40
何恩业, 李 海, 任湘湘等, 2008. BP人工神经网络在渤海湾叶绿素预测中的应用. 海洋预报, 25(2): 1—10
张 权, 王 燕, 王关锁等, 2011. 高分辨率浪-潮-流耦合数值预报系统的业务化运行与检验分析. 海洋科学进展,29(2): 129—136
张 韧, 蒋国荣, 2000. 赤道东太平洋海温及El Nino/La Nina的反演及预测. 解放军理工大学学报(自然科学版), 1(5):7—12
张文孝, 高国栋, 慕光宇等, 2006. 基于BP神经网络的海水盐度建模研究. 海洋技术, 25(4):39—41
张宏秋, 汪丽新, 张继赢, 2004. 夏季温度预报综合统计释用技术. 辽宁气象, (3): 18—19
苗世光, 孙桂平, 马 艳等, 2009. 青岛奥帆赛高分辨率数值模式系统研制与应用. 应用气象学报, 20(3): 370—379
欧素英, 杨清书, 2008. 人工神经网络模型在航道、港口潮水位预报中的应用. 水利水运工程学报, (2): 67—70
周 林, 杨成荫, 王汉杰等, 2009. 基于 CCA-BP-BPNN释用模型的太平洋 SST预报. 解放军理工大学学报(自然科学版), 10(4): 391—396
胡 波, 杜惠良, 郝世峰等, 2014. 一种统计技术结合动力释用的沿海海雾预报方法. 海洋预报, 31(5): 82—86
胡春梅, 余 晖, 陈佩燕, 2006. 西北太平洋热带气旋强度统计释用预报方法研究. 气象, 32(8): 64—69
堵盘军, 王丽琳, 管琴乐等, 2013. 人机交互式台风浪业务预报系统的研制及应用. 中国海洋大学学报(自然科学版),43(10): 16—24
黄良民, 钱宏林, 李锦蓉, 1994. 大鹏湾赤潮多发区的叶绿素α分布与环境关系初探. 海洋与湖沼, 25(2): 197—205
蒋宗礼, 2002. 人工神经网络导论. 北京: 高等教育出版社, 10—13
程戴晖, 杨美川, 2001. 上海浦西地区雾持续时间的统计释用预报. 气象, 27(7): 16—19
曾瑾瑜, 刘爱鸣, 高 珊等, 2015. 福建省沿海冬半年东北大风的数值预报释用方法研究. 海洋预报, 32(5): 61—68
魏泽勋, 徐腾飞, 王永刚等, 2015. 南海及周边海域风浪流耦合同化精细化数值预报与信息服务系统简介. 海洋技术学报, 34(3): 86—90
Chaudhari S, Balasubramanian R, Gangopadhyay A, 2008.Upwelling detection in avhrr sea surface temperature (SST)images using neural-network framework. In: IEEE International Geoscience and Remote Sensing Symposium,2008. Boston, MA, USA: IEEE, IV-926—IV-929
Deshmukh A N, Deo M C, Bhaskaran P K et al, 2016.Neural-network-based data assimilation to improve numerical ocean wave forecast. IEEE Journal of Oceanic Engineering, http://dx.doi.org/10.1109/JOE.2016.2521222 Filippo A, Torres A R Jr, Kjerfve B et al, 2012. Application of artificial neural network (ANN) to improve forecasting of sea level. Ocean & Coastal Management, 55: 101—110
Liu S Y, Xu L Q, Li D L, 2016. Multi-scale prediction of water temperature using empirical mode decomposition with back-propagation neural networks. Computers & Electrical Engineering, 49: 1—8
Tissot P E, Cox D T, Michaud P, 2002. Neural network forecasting of storm surges along the gulf of Mexico. In:Edge B L, Hemsley J M eds. Ocean Wave Measurement and Analysis. San Francisco, California, United States: ASCE,1535—1544
Vilibić I, Šepić J, Mihanović H et al, 2016. Self-organizing maps-based ocean currents forecasting system. Scientific Reports, 6: 22924
Zhao N, Han Z, 2015. A Simulation model of seawater vertical temperature by using back-propagation neural network.Polish Maritime Research, 22(S1): 82—88

