MASNUM-WAM海浪模式集合Kalman滤波同化研究*－I. 风场扰动对海浪模拟影响

孙 盟 尹训强, 杨永增,① 吴克俭

(1. 中国海洋大学海洋与大气学院 青岛 266100; 2. 国家海洋局第一海洋研究所海洋环境与数值模拟研究室 青岛 266061;3. 海洋国家实验室区域海洋动力学与数值模拟功能实验室 青岛 266071)

海浪资料同化是将数值模式与实测资料相结合,用于给出真实状态(又称为分析值)的最佳估计的一种有效方法, 对改善海浪模拟和预报效果具有至关重要的作用(Lionello et al, 1992)。相对于大气资料同化,海浪数据同化的研究起步较晚, 所采用的同化方法主要为变分方法(de las Heras et al, 1992, 1994; Bauer et al, 1996)、最优插值(Lionello et al, 1992; Young et al,1996; Hasselmann et al, 1997; Voorrips et al, 1997;Greenslade, 2001; Waters et al, 2013)、集合最优插值(Qi et al, 2016)和基于静态集合样本的滤波方法(孙盟等, 2014)等。然而, 在海洋环流模式和大气模式中广泛开展的集合Kalman滤波(Kalman, 1960; Kalman et al, 1961; Evensen, 1994; Burgers et al, 1998)同化方法在海浪数据同化中的应用相对较少。如何构造稳定可信的海浪模式集合运行成为制约海浪模式集合滤波同化应用的一个关键问题。

已知, 对于空间单点的某个变量进行多次采样,当采样次数足够多时, 该变量集合样本通常满足一定的统计分布(高斯分布)。针对同一变量, 对上述单点(又称中心点)附近的空间点进行多次采样, 同样的,当采样次数足够多时, 邻点的变量集合样本也满足一定的统计分布, 且邻点与中心点的变量集合样本存在一定的相关性, 这也是海浪同化中背景误差相关结构的信息来源(Kalnay, 2003)。根据上述分析, 全球尺度范围内的空间点均满足上述两条特征。由此, 为保证海浪模式集合滤波同化应用的合理性和正确性, 所构造的海浪模式集合需要满足上述两条基本特征, 这也是衡量海浪模式集合构造是否合理的重要指标。

由于海浪模式对初始场的敏感性较弱(Lionello,1992), 通过初始场扰动构造模式集合难以保证模式集合运行的稳定性。已知, 海浪模式由风场驱动, 若对风场进行持续有效的集合扰动, 可满足海浪模式集合运行的稳定性要求(Greenslade, 2004)。如何合理地对风输入进行扰动, 根据集合滤波方法的基本思想, 引入风场扰动量, 该扰动量的量级应与风场模拟误差的量级相当。本文提出三种风场集合扰动方案,分别为纯随机数、随机场和时间滞后的风场扰动方法。纯随机数方案是对当前时刻每个空间位置的风场矢量乘以满足某分布的随机数, 该集合扰动量必然满足一定的统计分布。随机场(Evensen, 1994)扰动方案是预先按照蒙特卡罗方法生成三维伪随机集合样本, 该集合样本总体均满足正态分布, 且单个样本在空间上具有局地性和平滑性, 然后将该集合样本作为扰动量, 叠加给当前风场, 构成风场集合。时间滞后方案是指利用6h间隔的风场偏差近似风场模拟误差, 由于当前时刻仅存在一个风场偏差样本, 因此对单个样本乘以满足某分布的随机数生成扰动集合。

基于上述分析, 本文利用 2014年 1月 ECMWF全球风场, 基于 MASNUM-WAM 海浪模式, 采用纯随机数、随机场和时间滞后方案, 构造风场集合, 由风场集合驱动生成海浪模式集合, 开展海浪数值模拟实验, 对海浪要素(有效波高)和二维波数谱集合样本进行统计分析, 对比三种风场集合扰动方案对于海浪模式的影响。上述为引言, 第一节介绍本文所采用的海浪模式和数据, 详细阐述了三种风场集合扰动方案, 第二节为集合海浪模式实验及结果分析, 最后一节为结论与展望。

1 风场集合扰动方案

1.1 模式与数据

本文采用球坐标系下的第三代海浪模式MASNUM-WAM(Marine Science and Numerical Modeling) (Yuan et al, 1992a, b; 杨永增等, 2005)。该模式应用了基于破碎波统计理论发展的海浪破碎耗散源函数(Yuan et al, 1986), 并采用复杂特征线嵌入计算格式。波数谱被离散成24个方向和25个波数,对应频率范围是0.042—0.413Hz。本文模式计算区域为: 79°S—65°N; 0°—360°E, 空间分辨率为 1.0°×1.0°,时间步长为15min, 模式每1h输出一次。地形数据为ETOPO5。

本文模式驱动风场数据采用2014年1月ECMWF风场(ERA-Interim), 该数据由欧洲中期天气预报中心提供。风场数据时间间隔为6h, 空间分辨率为1.0°×1.0°,覆盖范围为 90°S—90°N; 0°—360°E。此外, 本文中采用的三种风场集合扰动方案是针对全球海域提出的, 具有普遍适用性, 不局限于某海域或某时段, 研究中采用的全球风场数据具有足够时长即可。

1.2 风场扰动方案

为保证海浪集合模式运行的稳定性, 本文对驱动风场进行持续集合扰动, 即对当前时刻风场叠加扰动集合。首先, 需要确定风场的扰动幅度。若扰动幅度过大, 由于风场变化过大, 则容易出现海浪模式结果跳跃不连续、集合发散等问题; 若扰动幅度过小, 则容易出现集合收敛的情况, 与构造海浪集合模式的初衷相违背。由此, 风场扰动幅度应与风场模拟误差的量级相当。

确定风场模拟误差。已知在基于繁殖向量法的集合预报研究中, 数值模拟的误差可以分为三种分量:增长分量、恒定分量和衰减分量。其中, 增长分量将随着模式的积分不断成长, 恒定分量不随模式的积分改变, 衰减分量则随着模式的积分不断减小。与NMC方法(Parrish et al, 1992)类似, 采用固定时间间隔的模拟结果的差异可代替模式误差(孙盟等, 2014)。具体做法如式(1)所示。

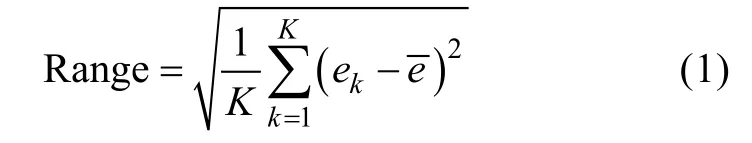
根据上述分析, 本文利用2014年 1月 ECMWF全球风场数据, 统计 6h间隔风速偏差的月平均值及标准差, 如图1所示。从图1可以看出, 6h间隔风速偏差月平均的浮动范围介于±0.2m/s之间, 全球平均约为 0m/s; 6h间隔风速偏差的标准差取全球平均为 1.6212m/s, 西风带区域标准差较大, 介于3—4m/s, 其他区域标准差普遍低于2m/s。

构造风场集合的基本思路是将扰动集合叠加到当前时刻的风场, 生成该时刻的风场集合。上文已确定风场扰动幅度(=1.6212m/s), 下面具体介绍三种风场集合扰动方案。

图1 2014年1月全球6h间隔风速偏差月平均及标准差空间分布(单位: m/s)Fig.1 Spatial distribution of global monthly average and standard deviation of difference between 6h-interval wind fields (2014/1)

(1) 方案A: 纯随机数扰动法

方案 A纯随机数扰动法中, 扰动集合由(-1,1)区间内满足平均分布的随机数,,ijnβ与风矢量的乘积构成, 如式(2)所示。若扰动幅度过小, 模式集合易出现收敛的趋势, 违背了风场集合扰动的初衷; 若扰动幅度过大, 可能会导致海浪模式的溢出或崩溃。为了避免上述问题, 引入控制扰动幅度的参数 αA, 将 αA·βi,j,n作为最终的风场扰动系数。

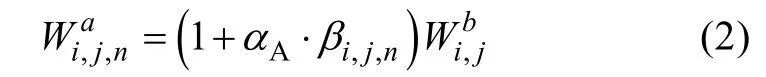
为了确定扰动幅度参数αA, 本文首先对2014年1月ECMWF全球风场数据进行月平均及标准差统计,如图 2所示。从图 2a可以看出, 西风带附近海域风速可达10m/s以上, 全球风速月平均为6.2678m/s; 从图 2b可以看出, 西风带附近海域标准差偏大, 普遍大于3m/s, 全球风速标准差的均值windσ为2.3841m/s。根据上文的分析, 已确定风场扰动幅度为 1.6212m/s, 结 合 式(2), 故 本 文 取= 0 .68。

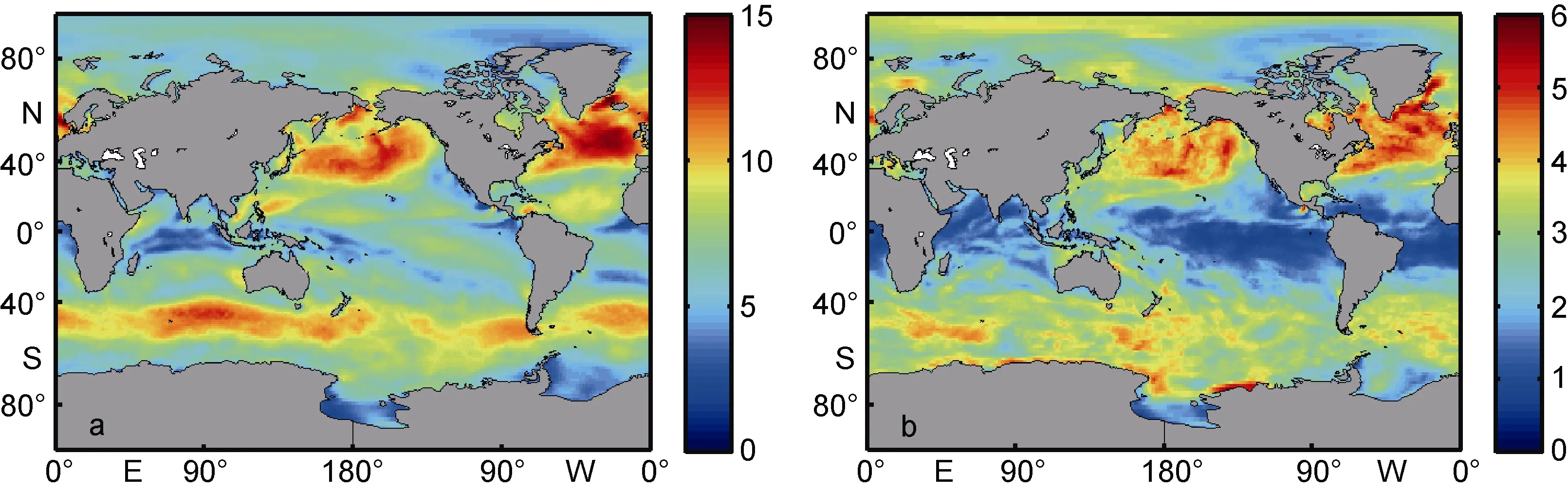
图2 2014年1月全球风速月平均及标准差空间分布(单位: m/s)Fig.2 Spatial distribution of global monthly average and standard deviation of wind field (2014/1)

(2) 方案B: 随机场扰动法

方案 B随机场扰动法中, 采用 Evensen(1994)的方法生成随机场λ, 作为扰动集合, 该三维伪随机集合样本总体服从正态分布, 单个集合样本空间上具有局地性和平滑性, 将该扰动集合叠加到风矢量场,构成风场集合, 如式(3)所示。与方案A类似, 引入控制扰动幅度的参数 αBn。

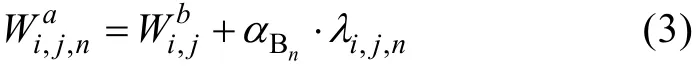
其中,,,ijnλ表示采用Evensen(1994)的方法所生成的随机场元素。

Evensen(1994)采用蒙特卡罗(Monte Carlo)方法所构造的随机场空间分布较为平滑, 单点空间相关性随距离的增加而减小, 具有较好的局地性, 将该随机场作为扰动形成驱动风场集合不会增加额外的空间梯度或破坏海浪模式本身的稳定性。构造随机场需要预先给出该随机场的空间相关距离尺度, 随机场作为扰动叠加到风场, 故其相关距离尺度应与风场相关距离尺度(本文取5°)一致。

(3) 方案C: 时间滞后扰动法

方案 C时间滞后扰动法中, 采用固定时间间隔的风场偏差与(-1, 1)区间内满足平均分布的随机数γ的乘积构造扰动集合, 如式(4)所示。驱动风场为大气模式结果, 其本身已包含大气模式的模拟误差, 利用固定时间间隔 Δt的风场偏差构造扰动样本, 该扰动样本保留了风场误差的演变及空间相关信息。由于两个时刻的风场偏差仅足以构造一个扰动样本, 由此,本文对该扰动样本乘以满足平均分布的随机数γn,从而生成扰动集合。与方案A类似, 考虑到风场扰动幅度对海浪模式的影响, 此处引入系数αC, 用于调整扰动幅度。

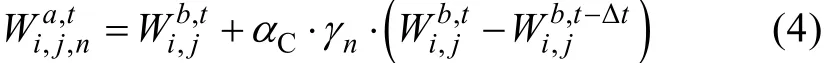
2 扰动实验与结果分析

利用 2014年 1月 ECMWF风场数据, 按照 1.2节中提出的扰动集合构造方案, 分别构造集合风场,用于驱动海浪模式集合, 开展为期一个月的海浪集合数值模拟实验, 集合样本数为 100。为了确保风场扰动的正确性, 本文首先对扰动集合样本进行抽样检查, 详见2.1节。驱动风场误差是海浪数值模拟误差的重要来源, 海浪模式本身对输入的驱动风场误差存在调整和自适应过程, 为考察不同的风场集合扰动方案对海浪模式的影响, 本文以海浪特征要素(有效波高)和二维波数谱为统计对象, 对比分析三种风场集合扰动方案对海浪模式的影响, 详见 2.2和2.3节。

2.1 扰动集合样本分析

对1.2节中的三种扰动方案, 以2014年1月1日0时扰动集合样本为例, 提取第一个样本, 分析其空间分布特征, 如图3所示。从图3可以看出, 方案A的扰动样本分布呈现沙盘化, 该现象由随机数对风场空间结构的瓦解造成; 方案 B的扰动样本呈现碎片状特征, 具有局地性和平滑性; 方案C的扰动样本保留了较多的风场空间结构信息(尺度较大), 这也是前两种方案所不具备的。

图3 扰动集合样本空间分布(单位: m/s)Fig.3 Spatial distribution of disturbance ensemble sample

2.2 有效波高集合样本统计分析

(1) 发散度时空分布

有效波高集合样本发散度可以反映模式集合发散的程度。为了分析有效波高集合样本发散度的时空分布特征, 采用式(5), 对减掉有效波高集合平均的三维变量S(样本发散度)进行统计分析。

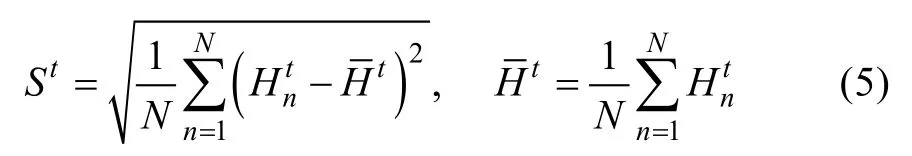
其中, H表示有效波高(空间二维场), 上划线表示集合平均, n=1, 2, …, N(N=100)。发散度S为具有时空属性的三维变量, 月平均的空间分布如图4所示; 对发散度 S进行空间(全球)平均后, 可得到随时间演变的曲线, 如图5所示。

从图4可以看出, 三种扰动方案的发散度在中高纬度地区普遍偏高(0.4m以上), 低纬度区域基本低于 0.15m; 与其他两种方案相比, 方案 B发散度空间整体分布更均匀。三种扰动方案的发散度在低纬度地区普遍偏小, 初步分析其原因为低纬度地区海浪有效波高随时间变化较小, 对集合扰动敏感性较弱。

从图5可以看出, 三种扰动方案的发散度曲线随时间变化不大, 纯随机数和随机场扰动法的发散度介于 0.1—0.2m, 时间滞后扰动法的发散度较前两者偏大, 在0.2—0.3m浮动。

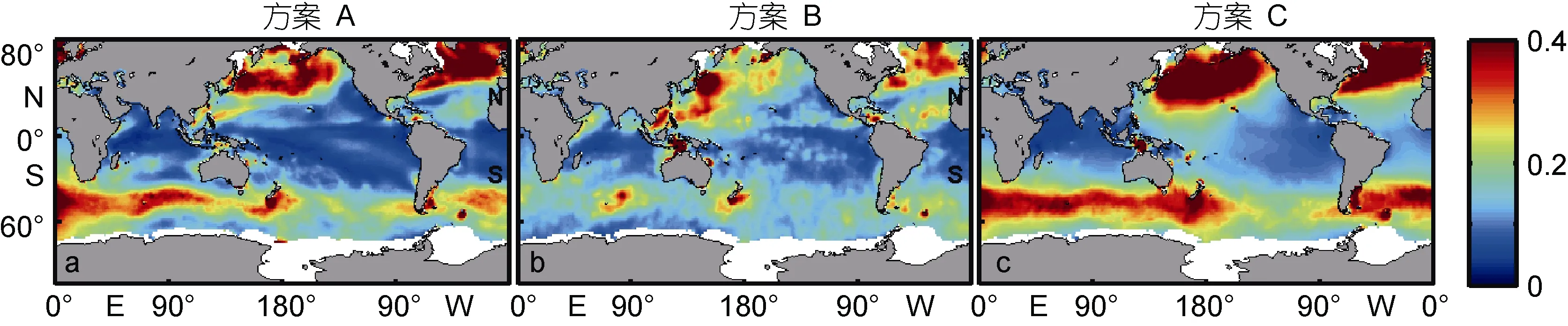
图4 有效波高集合样本发散度月平均的空间分布(单位: m)Fig.4 Spatial distribution of monthly-average divergence of SWH ensemble sample

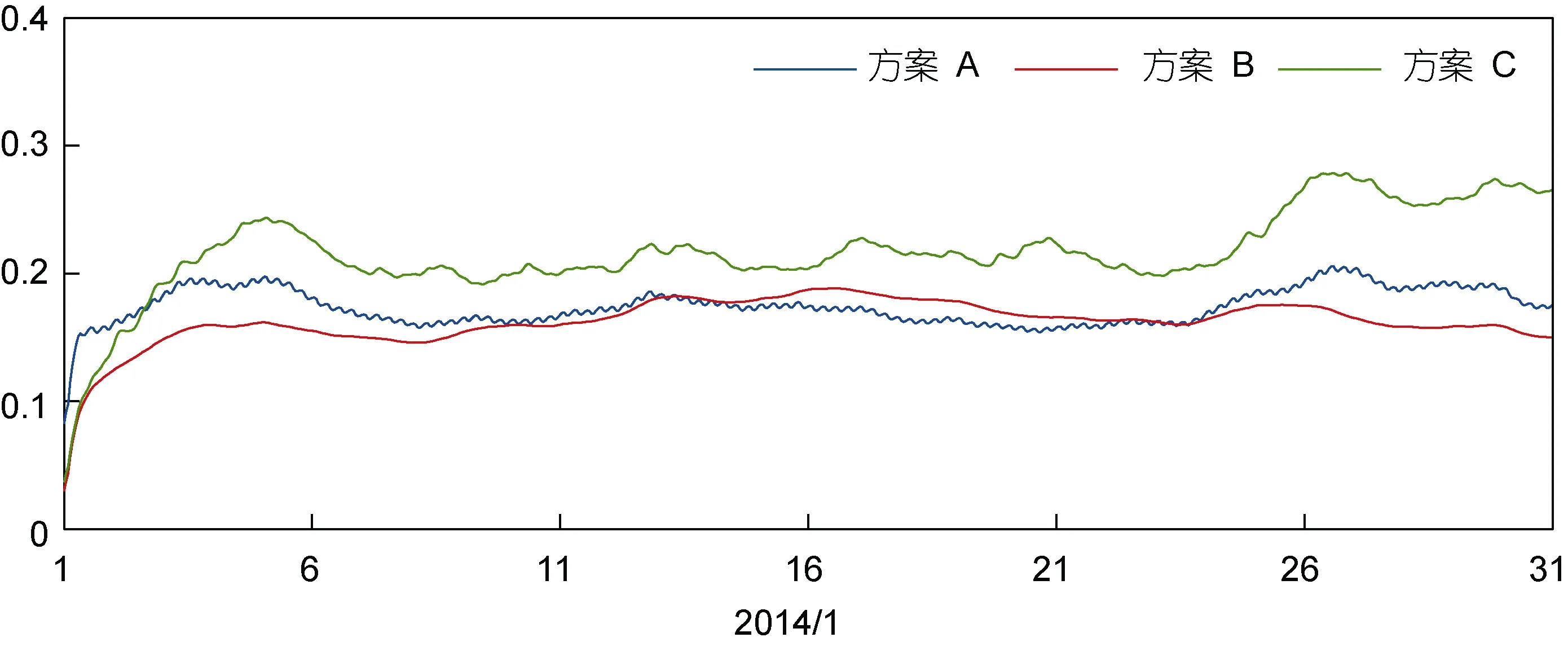
图5 有效波高集合样本发散度全球平均随时间变化曲线(单位: m)Fig.5 Global-average divergence of SWH ensemble sample

已知, 风场集合扰动方案优劣的重要判据是海浪模式集合是否具有均匀特征、稳定性和持续性。综上所述, 以有效波高作为海浪模式集合发散度的检验指标, 随机场扰动法所生成的海浪模式集合的发散度最佳; 其发散度空间分布平滑且基本均匀, 其发散度的全球平均随时间变化不大, 基本保持在 0.1—0.2m, 即风场扰动对有效波高的影响范围为0.1—0.2m。

(2) 离散概率密度分布

海浪模式集合样本发散度反映的是集合的整体特征, 良好的时空发散度是证明集合构造方案合理的必要条件。已知, 集合滤波方法中的集合需要满足一定统计分布, 即海浪模式集合样本的统计分布特征越明显, 风场扰动方案越合理。

选取某地理空间位置, 若其有效波高集合样本满足一定的统计特征, 那么, 该集合样本的概率密度分布可以反映模式集合的离散程度。由此, 将有效波高的值域, 划分成较小的网格区间, 统计该地理空间位置上某时刻的有效波高集合在该网格区间内的样本数, 得到相应的离散概率密度分布, 由不同时刻的有效波高集合样本, 可以得到该点离散概率密度随时间的演变过程。由于集合样本扰动量相对于有效波高是个小量, 故采用式(6), 对减掉有效波高集合平均的集合样本H*进行统计分析, 结果如图6所示。

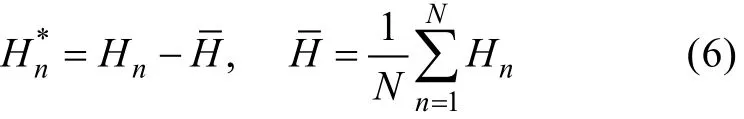
图 6 为空间点(60°E, 30°S)、(180°W, 0°)、(30°W,40°N)位置处集合样本H*的离散概率密度分布随时间的变化情况。从图6可以看出, 三种扰动方案的集合样本分布均接近正态分布, 但近似程度不一。由图6b、e、h可以看出, 虽然空间点不同, 但随机场扰动方案的集合分布特征保持稳定, 而纯随机数和时间滞后扰动方案在不同空间点的集合分布变化较大,时而发散时而收敛。即从随机误差统计分布的角度来讲, 随机场扰动为最佳方案。

图6 有效波高集合样本离散概率密度分布Fig.6 The probability density distribution of SWH ensemble sample divergence

(3) 相关系数月平均分布

利用有效波高集合样本可以计算某地理空间点与周围网格点的相关系数, 该相关系数反映了海浪同化调整过程中所需的权重信息, 是衡量海浪模式集合构造是否合理的关键指标之一。选定某地理空间点作为参考点, 以有效波高为统计量, 计算其他模式网格点相对于参考点的相关系数。每个时刻存在一个参考点相关系数的全场分布, 由此可以得到相关系数月平均的空间分布, 如图7所示。

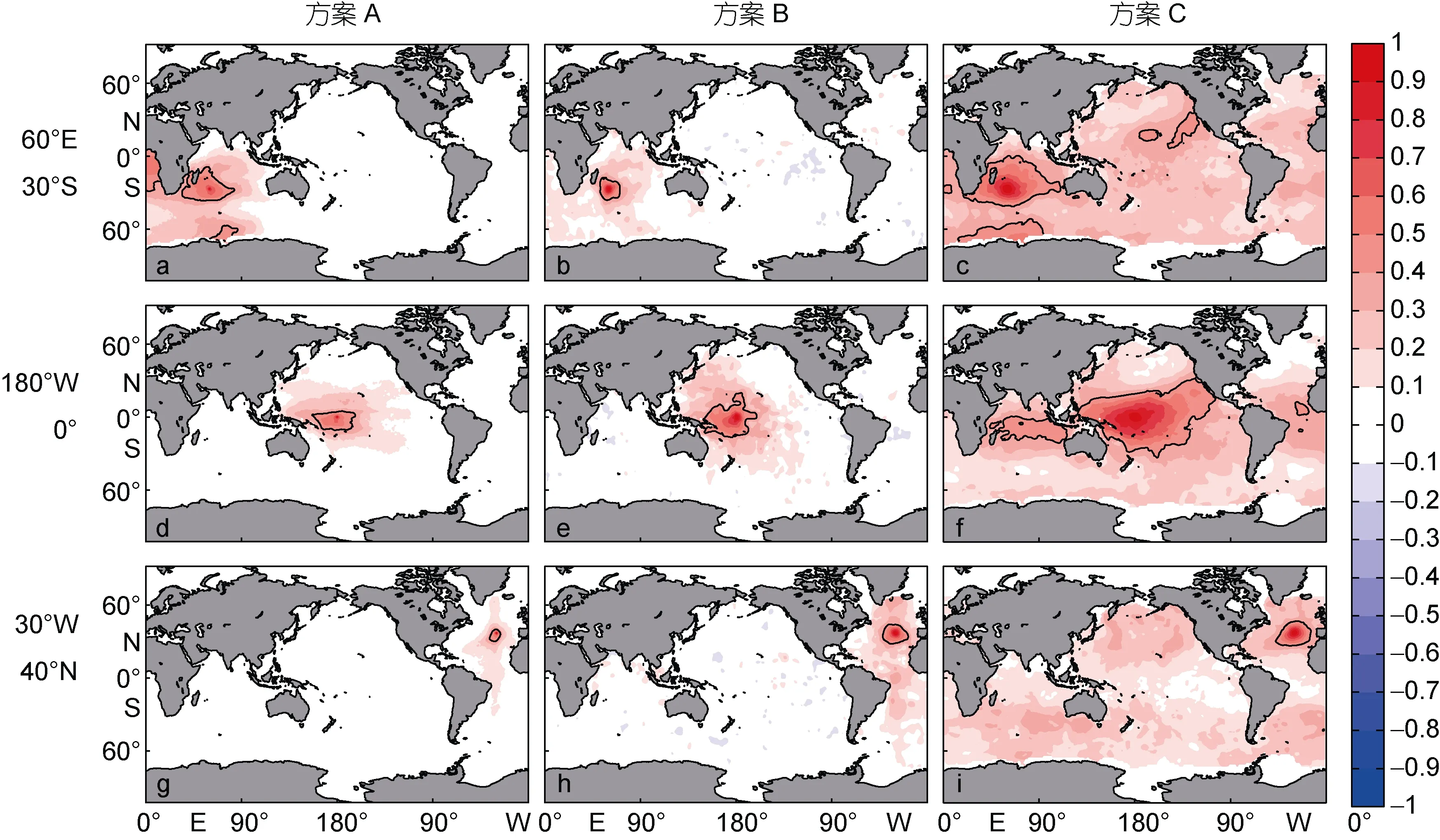
图7 有效波高空间相关系数月平均的空间分布Fig.7 Spatial distribution of monthly-average of SWH spatial correlation coefficient

图7a中存在三个相关系数0.4等值线区域, 即纯随机数扰动方案的相关系数分布存在虚假相关; 随机场扰动方案的相关系数分布具有较好的局地性,相关系数随着与参考点距离而增大, 相关尺度大小适宜; 时间滞后扰动方案的相关系数(大于 0.4)空间范围涉及到全球海域, 且存在虚假相关(如图7c、f所示), 其相应的同化调整计算量过大, 不适于实际应用。时间滞后扰动方案中, 同一时刻的扰动样本仅相差一个系数, 即同时刻的扰动集合样本间的相关性较大, 导致该方案有效波高空间相关尺度较大。从同化调整的角度来讲, 随机场扰动方法为最佳方案。

2.3 海浪谱集合样本统计分析

上述 2.2节中, 以海浪要素有效波高为例, 统计分析了三种风场集合扰动方案对海浪模式的影响,但海浪模式运行过程中是以二维海浪谱进行积分计算的, 有效波高仅为海浪谱的积分量, 难以细致地反映海浪的内部结构信息。由此, 为了了解三种风场集合扰动方案对海浪谱的影响, 针对海浪谱集合样本进行统计分析。

选取空间某点, 针对该点某时刻(此处取2014年1月31日24时)的二维波数谱(记为P), 按照公式(7)统计其发散度 SP(二维空间变量), 如图8所示。与上述发散度对应, 单点海浪谱集合样本平均的空间分布如图9所示。

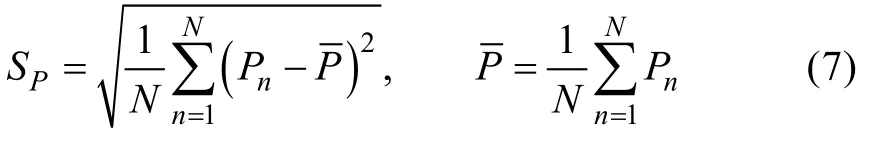
对比图8和图9可以看出, 海浪谱集合发散度主要集中于谱峰的位置, 且随与谱峰距离的增大而减小, 说明海浪模式集合扰动反映了海浪谱的主要部分, 并没有破坏海浪谱的主体结构。图8和图9中, 红色散点代表集合风场的方向(以下风、浪方向均指去向), (180°W, 0°)和(30°W, 40°N)位置处的集合风场方向与波向一致; (60°E, 30°S)位置处, 三种方案都存在两个谱峰(东北向和西南向), 但三种方案的集合风场方向都集中分布于西南向, 东北方向的谱峰可能是西风带位置的涌浪传播导致的, 这点也可以从相关系数分布图7a—c中看出, (60°E, 30°S)位置与西风带位置相关性较强。

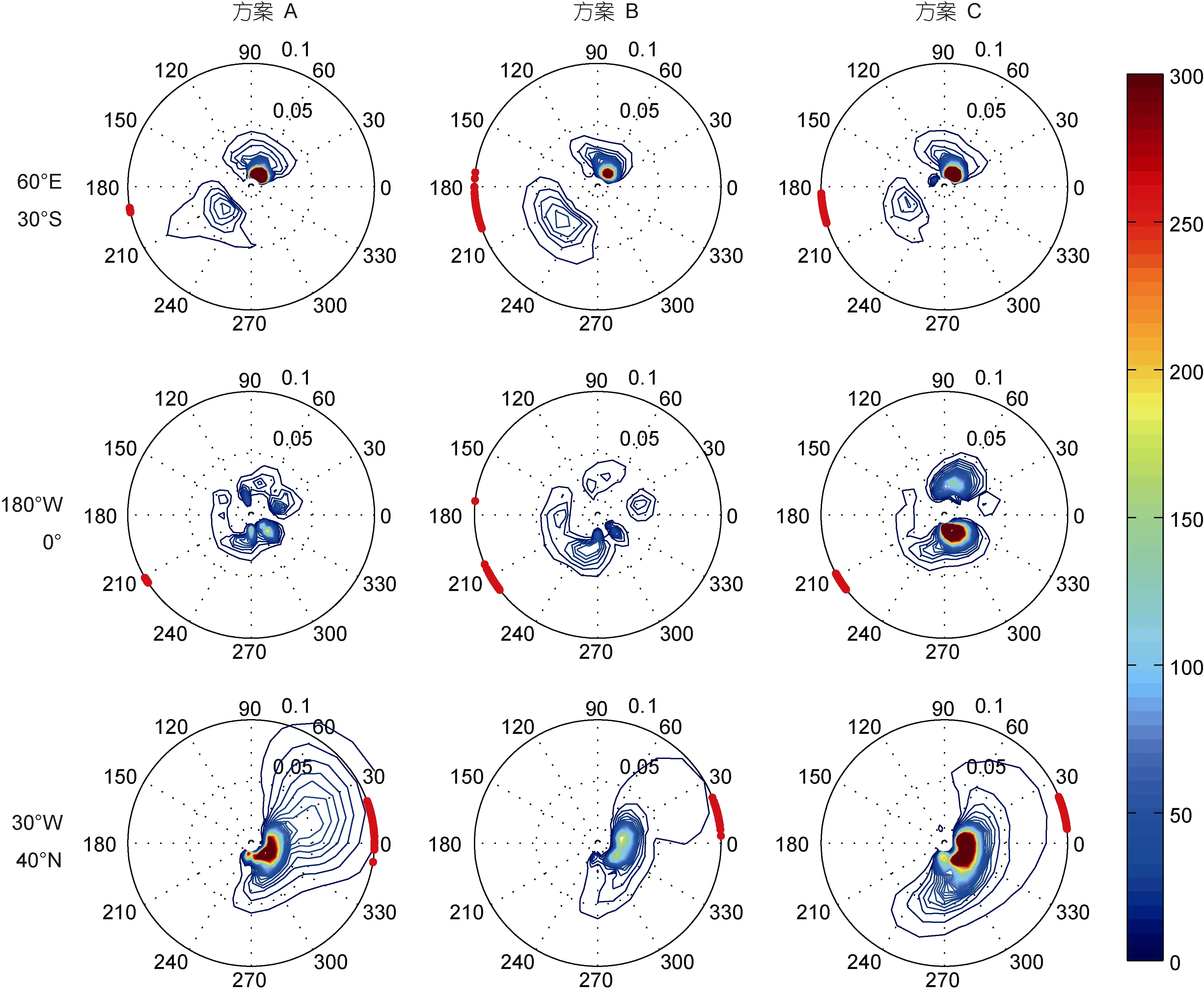
图8 二维波数谱集合样本发散度的空间分布(单位: m4)Fig.8 Spatial distribution of wavenumber spectrum ensemble sample divergence

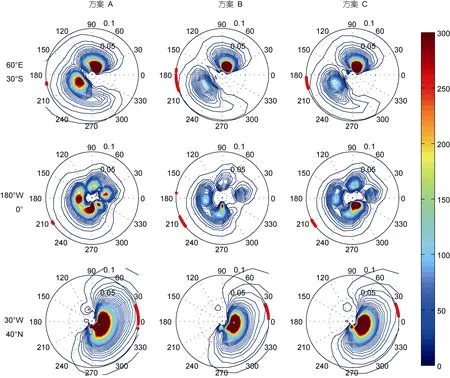
图9 二维波数谱集合样本平均的空间分布(单位: m4)Fig.9 Spatial distribution of average of wavenumber spectrum ensemble samples

3 结论和展望

现今, 集合 Kalman滤波方法在海洋和大气资料同化领域得到广泛研究和应用, 但具体到海浪资料同化相关研究较少。模式集合样本是否具有代表性是决定集合滤波同化效果的关键因素之一。考虑到海浪模式对初始场敏感性较弱, 本文通过对风场进行持续扰动, 构造海浪模式集合。所构造的海浪模式集合应当具有良好的时空发散度, 集合样本作为统计量应满足一定的统计分布, 此外, 由海浪模式集合统计得到背景误差相关信息应合理可信, 满足上述要求的模式集合样本方可应用于集合 Kalman滤波同化研究。

根据集合滤波的基本思想, 本文提出三种风场扰动方案: 纯随机数扰动、随机场扰动和时间滞后扰动。利用2014年1月ECMWF风场, 基于MASNUMWAM 海浪模式, 构造风场集合, 开展为期一个月的海浪模式集合运行实验, 以检验风场扰动方案对MASNUM-WAM海浪模式的影响。针对海浪要素(有效波高)和海浪谱进行集合样本统计分析, 结果表明,随机场扰动方案为最佳方案。随机场扰动方案的发散度在空间上分布均匀, 发散度随时间变化不大, 浮动范围为 0.1—0.2m; 有效波高集合样本的离散概率密度分布随时间变化的统计表明, 该方案的离散概率密度接近正态分布, 且不随空间点位置的改变而出现较大形变; 有效波高集合样本的相关距离尺度统计分析表明, 该方案的相关系数分布具有较好的局地性, 相关距离尺度适中, 适用于下一步的集合Kalman滤波同化研究。此外, 二维波数谱的集合样本发散度统计分析表明, 风场集合扰动方案没有破坏海浪谱的基本结构, 海浪谱集合发散度主要集中于谱峰附近。

综上所述, 随机场扰动方案为最佳风场集合扰动方案, 即利用 Evensen(1994)提出的方法生成随机场集合, 将该随机场集合作为扰动量叠加到风矢量场, 构成集合风场, 驱动海浪模式集合, 可用于后续的集合滤波同化实验。集合Kalman滤波方法是一种较为成熟的同化方法, 下一步工作将把随机场扰动方案与集合滤波方法相结合, 基于 MASNUM-WAM海浪模式, 开展海浪资料同化实验, 以检验集合滤波同化方法在海浪资料同化过程中的效果。

孙 盟, 尹训强, 杨永增, 2014. 静态集合样本的构造及其在全球海浪滤波同化中的应用. 海洋与湖沼, 45(5):918—927

杨永增, 乔方利, 赵 伟等, 2005. 球坐标系下 MASNUM 海浪数值模式的建立及其应用. 海洋学报, 27(2): 1—7

Bauer E, Hasselmann K, Young I R et al, 1996. Assimilation of wave data into the wave model WAM using an impulse response function method. Journal of Geophysical Research,101(C2): 3801—3816

Burgers G, Jan van Leeuwen P, Evensen G, 1998. Analysis scheme in the ensemble Kalman filter. Monthly Weather Review, 126(6): 1719—1724

De Las Heras M M, Janssen P A E M, 1992. Data assimilation with a coupled wind-wave model. Journal of Geophysical Research: Oceans, 97(C12): 20261—20270

De Las Heras M M, Burgers G, Janssen P A E M, 1994.Variational wave data assimilation in a third-generation wave model. Journal of Atmospheric and Oceanic Technology, 11(5): 1350—1369

Evensen G, 1994. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. Journal of Geophysical Research:Oceans, 99(C5): 10143—10162

Greenslade D J M, 2001. The assimilation of ERS-2 significant wave height data in the Australian region. Journal of Marine Systems, 28(1—2): 141—160

Greenslade D J M, 2004. The structure of the background errors in a global wave model. Adelaide, South Australia:University of Adelaide

Hasselmann S, Lionello P, Hasselmann K, 1997. An optimal interpolation scheme for the assimilation of spectral wave data. Journal of Geophysical Research: Oceans, 102(C7):15823—15836

Kalman R E, 1960. A new approach to linear filtering and prediction problems. Journal of basic Engineering, 82(1):35—45

Kalman R E, Bucy R S, 1961. New results in linear filtering and prediction theory. Journal of basic engineering, 83(1):95—108

Kalnay E, 2003. Atmospheric Modeling, Data Assimilation and Predictability. Cambridge: Cambridge University Press

Lionello P, Günther H, Janssen P A E M, 1992. Assimilation of altimeter data in a global third-generation wave model.Journal of Geophysical Research: Oceans, 97(C9):14453—14474

Parrish D F, Derber J C, 1992. The National Meteorological Center's spectral statistical-interpolation analysis system.Monthly Weather Review, 120(8): 1747—1763

Qi P, Cao L, 2016. The Assimilation of Jason-2 Significant Wave Height Data in the North Indian Ocean Using the Ensemble Optimal Interpolation. IEEE Transactions on Geoscience and Remote Sensing, 54(1): 287—297

Voorrips A C, Makin V K, Hasselmann S, 1997. Assimilation of wave spectra from pitch-and-roll buoys in a North Sea wave model. Journal of Geophysical Research: Oceans, 102(C3):5829—5849

Waters J, Wyatt L R, Wolf J et al, 2013. Data assimilation of partitioned HF radar wave data into Wavewatch III. Ocean Modelling, 72: 17—31

Young I R, Glowacki T J, 1996. Assimilation of altimeter wave height data into a spectral wave model using statistical interpolation. Ocean Engineering, 23(8): 667—689

Yuan Y L, Hua F, Pan Z D et al, 1992a. LAGFD-WAM numerical wave model-I. basic physical model. Acta Oceanologica Sinica, 10(4): 493—488

Yuan Y L, Hua F, Pan Z D et al, 1992b. LAGFD-WAM numerical wave model-Ⅱ. characteristics inlaid scheme and its application. Acta Oceanologica Sinica, 11(1): 12—23

Yuan Y L, Tung C C, Huang N E, 1986. Statistical characteristics of breaking waves. In: Phillips O M, Hasselmann K eds.Wave Dynamics and Radio Probing of the Ocean Surface.New York: Springer, 265—272