间隙条件下刨煤机刨头接触碰撞动态特性研究

间隙条件下刨煤机刨头接触碰撞动态特性研究

毛君1，张瑜1，刘占胜2，李国平3，陈洪月1，郭辰光1

(1.辽宁工程技术大学机械工程学院，辽宁阜新123000;2. 中国煤矿机械装备有限责任公司，北京100011; 3.中煤张家口煤矿机械有限责任公司，河北张家口076250)

摘要：考虑了刨头与滑架之间的水平和竖直间隙，通过点到直线的距离来进行碰撞检验的方法，构造了刨头与滑架接触碰撞判别条件。采用非线性弹簧阻尼接触力模型，建立了间隙条件下的刨头三自由度碰撞振动动力学模型，并采用龙哥库塔法进行数值仿真分析，分析表明间隙条件下刨头与滑架之间产生了单点、两点、三点碰撞；刨头与滑架各接触点的最大碰撞力随着竖直间隙的增大而先增大随后降低，随着水平间隙增大而逐渐增大。采用RecurDyn对刨头动力学模型进行了仿真，其结果与理论分析相吻合。

关键词：刨煤机；接触碰撞；间隙；动态特性

中图分类号:TD421.62

文献标志码：A

DOI:10.13465/j.cnki.jvs.2015.19.036

Abstract:Horizontal clearance and vertical one between plough head and sliding framework were considered. The criterion of contact-impact between plough head and sliding framework were established with the collision detection method using the distance between a point and a line. The plough head’s dynamic equation with 3-DOF vibro-impact under clearance conditions was established by using a nonlinear spring-damper contact force model. The numerical simulation was performed by using Runge-Kutta method. The results showed that there are single-point impact, two-point impact and three-point impact between plough head and sliding framework under clearance conditions; the maximum collision force at each contact point between plough head and sliding framework firstly increases and then decreases with increase in vertical clearance, and increases with increase in horizontal clearance. The plough head’s dynamic model was adopted for simulation with RecurDyn. The results agreed well with those of the theoretical analysis.

Dynamic characteristics of plough head under contact-impact with clearances

MAOJun1,ZHANGYu1,LIUZhan-sheng2,LIGuo-ping3,CHENHong-yue1,GUOChen-guang1(1. College of Mechanical Engineering, Liaoning Technical University, Fuxin 123000, China;2. China National Coal Mining Equipment Co. Ltd, Beijing 100011, China; 3. China Coal Zhangjiakou Coal Mining Machinery Co. Ltd, Zhangjiakou 076250, China)

Key words:plough; contact-impact; clearance; dynamic characteristics

刨煤机作为开采薄煤层的主要采煤机械而被广泛应用。刨头是刨煤机系统的工作机构，其动态特性直接影响刨煤机的工作性能。康晓敏等[1]对刨头的稳定性进行了分析，得出刨头高度和刨削深度对刨头稳定性产生了一定的影响。郝志勇等[2]对滑行刨煤机刨头进行了三维受力分析。李晓豁等[3]建立了刨头在截割煤层时的载荷数学模型，分析了刨头不同部位载荷的分布。贺洪华等[4]建立了刨头平面振动的动力学方程，分析了刨头平面振动特性。以上学者在研究过程中均未考虑间隙对刨头动态特性的影响。

由于制造装配的需要以及刨头相对滑架运行时产生磨损等原因，刨头与滑架之间存在一定的间隙，而间隙对刨头的运动稳定性产生较大的影响，使刨头在运行过程中与滑架产生碰撞与冲击，从而影响其动力特性、可靠性等。可见研究间隙条件刨头的碰撞振动特性具有工程实际意义。针对间隙碰撞振动，金栋平等[5]阐述了机械系统碰撞振动的典型现象，并提炼了间隙碰撞振动的解析方法,研究了碰撞振动系统的非线性动力学行为。占甫等[6-7]从不同角度分析了三维间隙空间可展机构的动力学行为。Bapat等[8-13]采用连续接触碰撞力模型对不同机构的接触碰撞做了大量研究。如Ravn[14]采用连续接触模型分析了对曲柄滑块机构的动态特性的影响。Flores[15]建立了间隙旋转铰的接触条件以及采用连续接触碰撞力模型，对间隙条件下的平面四连杆机构动态特性进行了分析。

本文基于以上分析，建立了考虑间隙条件的刨头三自由度碰撞振动动力学模型，提出了刨头与滑架的碰撞判别条件。并采用数值方法对该动力学模型进行求解，分析了间隙条件下刨头的动态特性，以及不同间隙量对刨头动态特性的影响。

1碰撞条件

将刨头与滑架相对运动模型简化，见图1。由于刨头与滑架之间存在间隙，刨头在外部激励的作用下会出现摆动以及竖直方向、水平方向移动，导致刨头在运行过程中与滑架出现分离，接触。为了描述刨头的运动特性，需要判断刨头在运动过程中与滑架碰撞的条件。

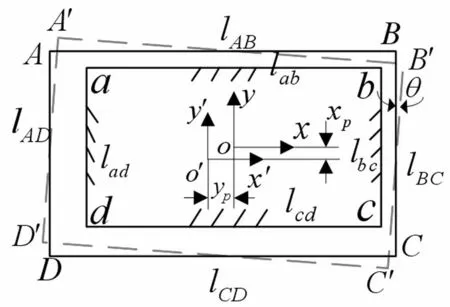
图1　 刨头间隙碰撞简化平面图 Fig.1 Simplified planar graph of clearance impact of coal plow

设图1中矩形abcd为滑架固定不动，矩形ABCD为刨头相对滑架摆动、移动，判别其相对运动过程中是否产生重叠的算法，其原理为：检验滑架的各顶点到刨头对边的距离之和是否大于其相邻边长，如果大于则产生碰撞，若果等于则未碰撞。如判断滑架中顶点b是否与刨头产生碰撞的条件为：检验顶点b到边lAB的距离与顶点b到边lCD距离之和是否大于边lBC长。

本文以判断b点产生碰撞条件为例。设刨头运动之前各顶点坐标为Xi=(xi,yi),,i=1,2,3,4，b点坐标为(x0,y0)。则刨头运动之后位置为图1中矩形A′B′C′D′，其各点坐标Nj=(xj,yj),j=1,2,3,4，其转化表达式为：

Nj=P1,2·XTi+M

(1)

式中，P1,2为旋转矩阵，刨头逆针转动为

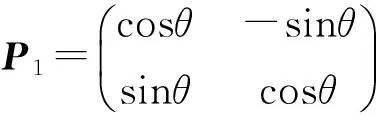
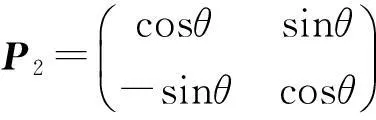
则刨头顺时针摆动且移动之后，各点坐标为：

NTj=(xicosθ+yisinθ+xp,-xisinθ+yicosθ+yp)

令

xNj=xicosθ+yisinθ+xp，

yNj=-xisinθ+yicosθ+yp

则根据两点直线公式得直线lAB：

(yN1-yN2)x+(xN2-xN1)y+(xN1yN2-xN2yN1)=0

lCD：(yN3-yN4)x+(xN4-xN3)y+(xN3yN4-xN4yN3)=0

令A0=yN1-yN2，B0=xN2-xN1，C0=xN1yN2-xN2yN1，A1=yN3-yN4，B1=xN4-xN3，C1=xN3yN4-xN4yN3，根据点到直线距离，点b到直线lAB与lCD的距离之和为：

(2)

此时，如果滑架b点与刨头产生碰撞，则

s>lBC

(3)

如果滑架b点与刨头未产生碰撞，则

s=lBC

(4)

在外部激励作用下，刨头与滑架在二维平面内将产生三种接触碰撞形式，图2为刨头顺时针摆动时，刨头与滑架产生的三种不同碰撞状态，逆时针同理。刨头与滑架在三维空间内简图见图3(a)。在外部激励作用下，刨头将会与滑架产生如下几种碰撞状态：①当刨头水平摆动时，刨头上方前端边lAB(或者前端下方边)以及后端下方边(或者后端上方边)与滑架产生碰撞见图3(b)；②当刨头侧向摆动时，刨头前端左边上下两边(或者前端右方下方边)以及后端右方的边(或者后方左端上下两边)与滑架产生碰撞见图3(c)；③刨头摆动时同样会产生单点瞬时碰撞见图3(d)；④由于刨头自重的原因，刨头上端面与滑架产生面碰撞见图3(e)，同时在外部激励作用下，刨头右端面也会与滑架产生面碰撞。本文仅研究二维平面刨头与滑架的碰撞动力学特性。

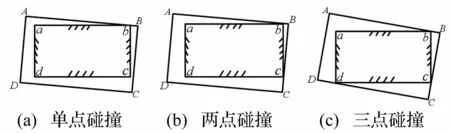
图2　三种接触碰撞状态 Fig.2 Three states of contact-impact

图3　三维空间接触碰撞状态 Fig.3 Contact-impact of three-dimensional space

2间隙条件下刨头动力学模型建立

为了分析间隙对刨头与滑架接触碰撞动态特性的影响，将刨煤机刨头与滑架机构简化为图4受力模型，以滑架中心处为坐标原点，见图4，设坐标系为xoy。定义θ为刨头转动角位移(设逆时针转动为正)，x为刨头水平位移，y为刨头竖直位移，根据牛顿运动定律，建立刨头摆动、竖直移动和水平移动相耦合的三自由度运动平衡微分方程：

图4　刨头受力模型 Fig.4 Force model of coal plow

(5)

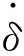
(6)

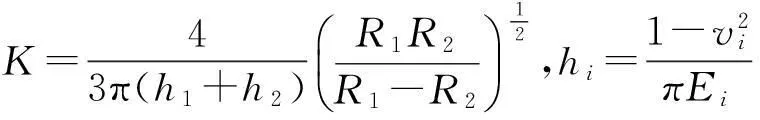
3数值模拟

根据式(5)所建立刨头三自由度动力学模型，采用龙格一库塔方法对其进行数值求解，并利用Matlab软件编程进行仿真分析，其仿真流程图见图5。

本文以某种刨头的结构参数为例进行数值求解，m=2430kg，I=1265kg·m2，lab=lcd=0.27m，lad=lbc=0.33m，lx1=0.72m，lx2=0.415m，lx3=0.01m，ly=lyN=0.615m，lg=0.255m；刨头所受外部激励以及激励频率，Fy=11kN，Fx1=92kN，Fx2=36kN，Fx3=96kN，ω=2rad/s。通过数值仿真得到含间隙碰撞模型在间隙条件下非线性响应的时域波形图和碰撞力图。

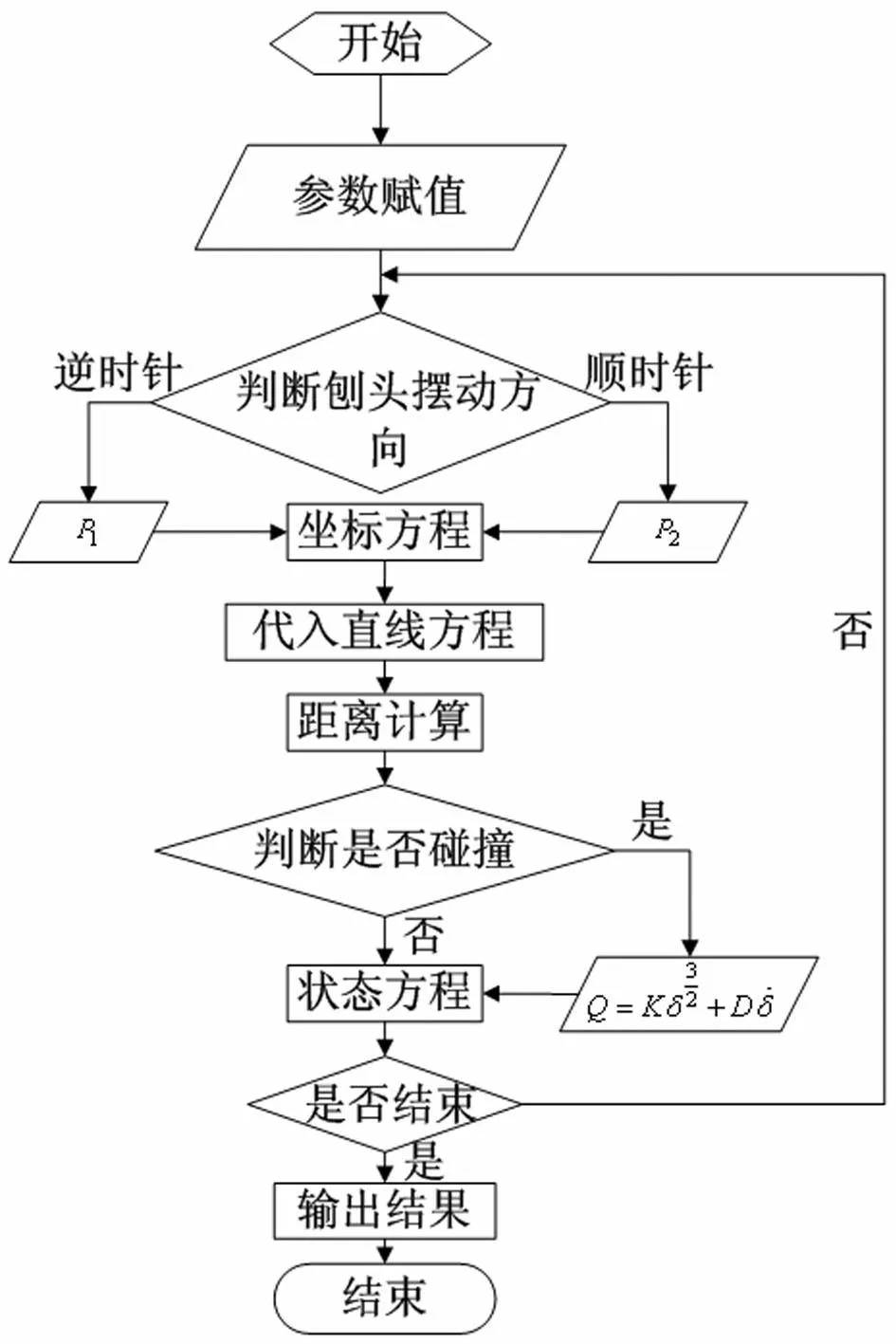
图5　仿真流程图 Fig.5 Flow chart of simulation

图(6)为竖直间隙为30 mm、水平间隙为25 mm时刨头质心与滑架质心相对运动时域图。从图中可知，由于刨头与滑架之间存在碰撞，使得刨头质心摆角幅值及刨头质心水平、竖直移动量出现了不同程度的振荡。而竖直振动受重力影响，其反向振动大于正向振动幅度。

图7为刨头与滑架各点碰撞力。从图中可知，由于间隙的存在，刨头与滑架各点均产生了间断碰撞。对图7中各点碰撞力同时取平均值和最大值，则刨头与滑架各点逆时针碰撞力最大平均值为a点，其值为74kN，刨头与滑架各点顺时针的碰撞力最大平均值产生在b点，其值为82kN，而刨头与滑架a,b,c,d各点逆时针碰撞力最大值同样产生在a点：其值为153kN，刨头与滑架各点顺时针的碰撞力最大值为b点，其值为177kN。由于刨头重力而引起偏心力的影响，滑架上面a,b两点所受碰撞力均值以及最大值均大于c,d两点。

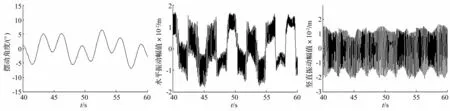
图6　 刨头质心与滑架质心相对运动时域图 Fig.6 Time domain chart of mass center relative motion of sliding framework and coal plow

图7　 刨头与滑架各点碰撞力 Fig.7 The collision force of sliding framework and coal plow

将图7刨头与滑架各点碰撞力局部放大。见图8为刨头逆时针与滑架各点碰撞力局部放大图，从图中可知，刨头与滑架存在单点、两点及三点逆时针碰撞，以两点碰撞为主。如在53.8s时刻，刨头仅与滑架b点逆时针碰撞，在53.03s时刻，刨头与滑架a,d点产生两点碰撞。在52.95s时刻，刨头与滑架a,b,d三点产生了逆时针碰撞。图9为刨头顺时针与滑架各点碰撞力局部放大图，从图中可知，刨头与滑架同样存在单点、两点及三点顺时针碰撞，如在56.55s时刻，刨头仅与滑架a点产生碰撞，在56.8s时刻，刨头与滑架b,c两点碰撞。在57.85s时刻，刨头与滑架a,b,c三点产生了逆时针碰撞。可见，由于间隙的存在，刨头与滑架各点产生了单点、两点、三点碰撞。

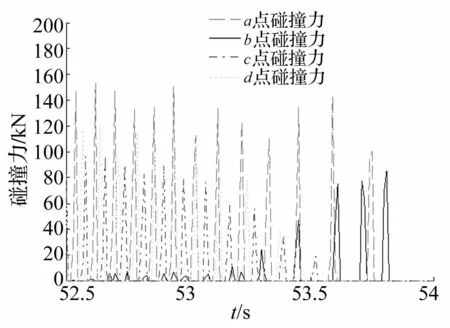
图8　 刨头与滑架逆时针碰撞局部放大图 Fig.8 Local enlarging graphs of counterclockwise collision between sliding framework and coal plow

图9　 刨头与滑架顺时针碰撞局部放大图 Fig.9 Local enlarging graphs of clockwise collision between sliding framework and coal plow

4间隙对刨头稳定性的影响

图10为水平间隙为20mm，竖直间隙从20～30 mm变化时各点最大碰撞力变化规律。从图中可知，刨头与滑架各点的最大碰撞力随着竖直间隙的增大而先增大随后降低。图11为竖直间隙为20mm，水平间隙从20～30 mm变化时各点最大碰撞力变化规律。从图中可知，刨头与滑架各点的最大碰撞力随着水平间隙增大而逐渐增大。此外，从图10、图11可知，随着间隙的增大，刨头与滑架的最大碰撞力发生在a点或者b点。

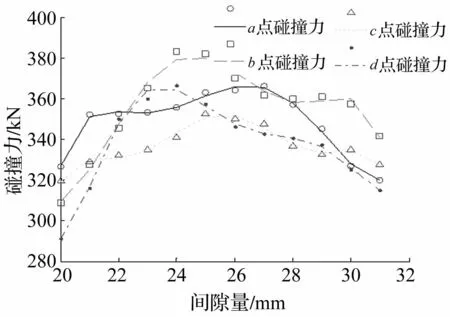
图10　 竖直间隙变化时各点最大碰撞力 Fig.10 The maximum collision force with vertical clearance changes

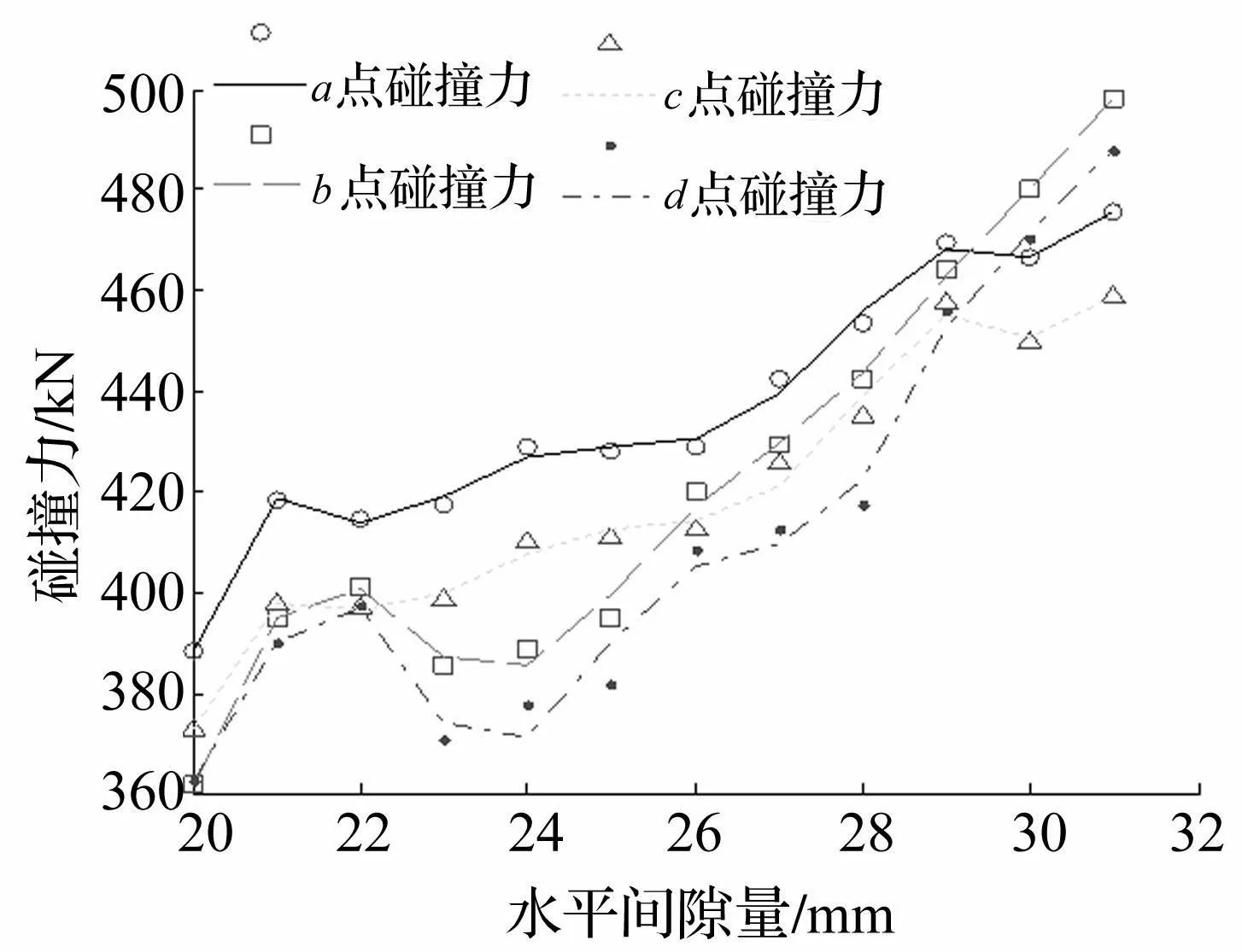
图11　水平间隙变化时各点最大碰撞力 Fig.11 The maximum collision force with horizontal clearance changes

5模型验证

为了验证模型的正确性，在Pro/e软件中建立含间隙刨头与滑架模型，并将其映射到RecurDyn软件中进行多刚体动力学仿真。在RecurDyn中，设置仿真时间20s，定义接触刚度与阻尼以及所受激励，其模型见图12。

图12　RecurDyn仿真模型 Fig.12 RecurDyn simulation model

图13为刨头4个内表面与滑架碰撞力局部放大图。从图中可知，标注1处为刨头逆时针摆动时单面与滑架产生碰撞，2处为刨头顺时针摆动时两面与滑架产生碰撞，3处为刨头顺时针摆动时三面与滑架产生碰撞。可见其碰撞规律与前述理论分析结果基本吻合，从而验证了该方法的有效性。

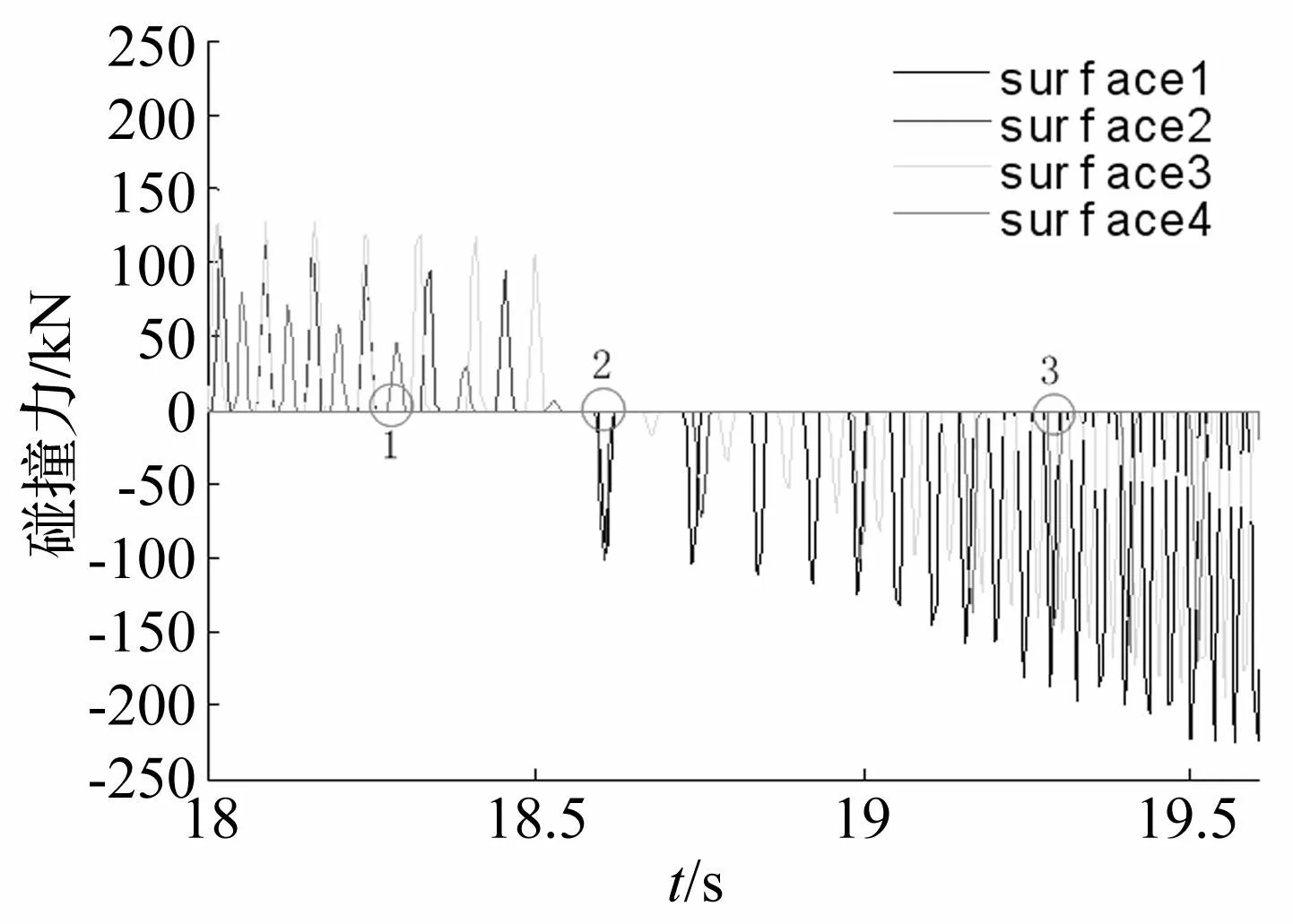
图13　模型仿真碰撞力 Fig13.Simulation collision force of model

基于第4节所分析的不同间隙对刨头稳定性的影响，通过RecurDyn对其进行验证。选取三种竖直间隙、水平间隙：20mm、25mm、30mm进行仿真，其仿真结果见图14～图15。可见碰撞趋势与4节分析相符，说明理论分析的正确性。

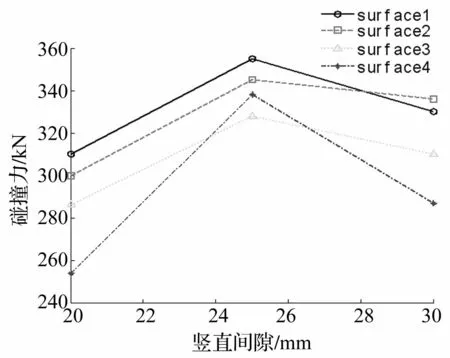
图14　增加竖直间隙仿真结果图 Fig.14 Simulation results figure as horizontal clearance increasing

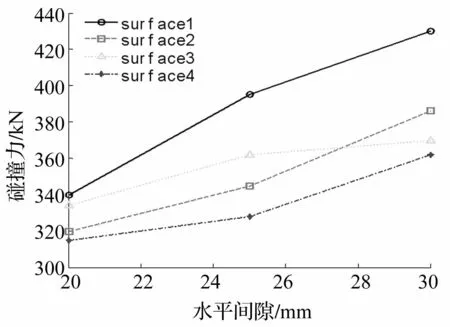
图15　增加水平间隙仿真结果图 Fig.15 Simulation results figure as vertical clearance increasing

6结论

(1)由于间隙的存在，使得刨头动态特性发生了变化，具体表现为：使得刨头质心摆角幅值及刨头质心水平、竖直移动量出现了不同程度的振荡；刨头与滑架之间产生了单点、两点、三点碰撞；可见，间隙使得刨头的运动稳定性降低。

(2)在一定间隙范围内，当水平间隙固定时，刨头与滑架各点的最大碰撞力随着竖直间隙的增大而先增大随后降低；当竖直间隙固定时，刨头与滑架各点的最大碰撞力随着水平间隙增大而逐渐增大。因此，在保证刨头正常运行的情况下，适当降低刨头水平间隙，将竖直间隙控制在一定范围内。

(3)同时，为验证结论的可靠性，采用RecurDyn对刨煤机刨头动力学模型进行了模拟仿真，对刨头与滑架的碰撞规律以及间隙对刨头与滑架碰撞力影响趋势的仿真结果与理论分析结果基本吻合。证实了结论的可靠性。

参考文献

[1]康晓敏，李贵轩. 刨煤机刨头的稳定性分析[J].中国机械工程，2012,23(22):2739-2742.

KANG Xiao-min, LI Gui-xuan.Stability analysis of plow body of Coal plow[J]. China Mechanical Engineering, 2012,23(22):2739-2742.

[2]郝志勇，李贵轩，康晓敏. 滑行刨煤机刨头的受力分析[J]. 煤矿机电，2005(1):21-23.

HAO Zhi-yong, LI Gui-xuan, KANG Xiao-min. The force analysis of sliding plough body[J].Colliery Mechanical & Electrical Technology, 2005(1):21-23.

[3]李晓豁，付伟丽，张飞虎，等. 刨头上不同位置刨刀的随机载荷模拟研究[J]. 微计算机信息，2011, 27(12):24-26.

LI Xiao-huo, FU Wei-li, ZHANG Fei-hu. Simulation and study of random loads on plow tools at different locations of plough head[J]. Microcomputer Information, 2011, 27(12):24-26.

[4]贺洪华，陆俭. 刨煤机刨头的振动分析与仿真研究[J].煤矿机电，2013(22):5-7.

HE Jin-hua, LU Jian.Vibration analysis and simulation study of coal plough head[J]. Colliery Mechanical & Electrical Technology, 2013(22):5-7.

[5]金栋平，胡海岩.碰撞振动与控制[M].北京:科学出版社，2005.

[6]占甫，关富玲. 含三维间隙铰空间可展机构动力学数值分析[J].浙江大学学报，2009,43(1):177-182.

ZHAN Pu, GUAN Fu-ling.Dynamics numerical analysis of space deployable mechanism with three-dimensional clearance revolute joint[J]. Journal of Zhejiang Uniwersity, 2009,43 (1):177-182.

[7]周益君，关富玲. 考虑杆件弹性和三维间隙铰机构动力学研究[J].哈尔滨工业大学学报，2012,44 (10);122-127.

ZHOU Yi-jun, GUAN Fu-ling.Dynamics analysis of mechanisms with elastic bars and three-dimensional clearance revolute joints[J]. Journal of Harbin Institute of University, 2012,44 (10):122-127.

[8]Bapat C N. The general motion of an inclined impact damper with friction [J]. Journal of Sound Vibration，1995, 184(11):417-427.

[9]Ahn K Y, Ryu B J. A modeling of impact dynamics and its application to impact force prediction[J]. Journal of Mechanical Science and Technology, 2005,19(1):422-428.

[10]Flores P, Ambrosio J, Pimenta Claro J C, et al. Influence of the contact impact force model on the dynamic response of multibody systems [J].Proceedings of the Institution of Mechanical Engineers，Part K: Journal of Multi-body Dynamics, 2006,220 (1):21-34.

[11]Gerasimov S A. Vibrational-impact dynamics [J]. Russian Engineering Research,2013,33(3):130-132.

[12]Flores P, Ambrósio J. On the contact detection for contact-impact analysis in multibody systems [J].Multibody System Dynamics,2010, 24(1): 103-122.

[13]Flores P,Ambrósio J,Pimenta Claro J C. Contact-impact force models for mechanical systems[J]. Kinematics and Dynamics of Multibody Systems with Imperfect Joints, 2008,34:47-66.

[14]Ravn P. A continuous analysis method for planar multibody systems with joint clearance [J]. Multibody system dynamics, 1998, 2:1-24.

[15]Flores P,Ambr6sio J,Pimenta Claro J C, et al. Dynamic behaviour of planar rigid multi-body systems including revolute joints with clearance[J].Proceedings of the Institution of Mechanical EngineersPart K: Journal of Multi-body Dynamics,2007, 221(2):161-174.

[16]Tasora A, Prati E, Silvestri M. A compliant measuring system for revolute joints with clearance [C] //AITC-AIT 2006 International Conference on Tribology. Parma：Parma University, 2006:726-732.

[17]Muvengei O, Kihiu J, Ikua B. Dynamic analysis of planar rigid-body mechanical systems with two-clearance revolute joints [J]. Nonlinear Dynamics, 2013, 73:259-273.