大跨度铁路斜拉桥冲击系数的影响因素研究
大跨度铁路斜拉桥冲击系数的影响因素研究
李永乐1,鲍玉龙1,董世赋1,2,曾永平3,向活跃1
(1. 西南交通大学土木工程学院,成都610031; 2. 湖北省交通规划设计院,武汉430051;3.中铁二院工程集团有限责任公司,成都610031)
摘要:为研究列车编组等因素对大跨度铁路斜拉桥冲击系数的影响,针对大跨度铁路斜拉桥车致振动的特点,采用车桥耦合振动的方法,探讨了不同列车运营条件对桥梁局部构件的冲击效应的影响。通过自主研发车桥分析软件BANSYS,分析了大跨度铁路斜拉桥的动力响应,讨论了列车编组、轨道不平顺、行车方向和列车类型等因素对斜拉桥各部件冲击系数的影响。研究表明:进行车桥动力计算和现场动力试验时,应尽量采用与实际列车相同或相似的列车编组;列车行车方向不同时,构件同一位置处冲击系数相差较大。
关键词:大跨度铁路斜拉桥;车桥耦合振动;冲击系数;影响因素;列车编组
中图分类号:U443
文献标志码:A
DOI:10.13465/j.cnki.jvs.2015.19.022
Abstract:In order to investigate the effects of some factors including train formation on the impact coefficient of long-span railway cable-stayed bridges, according to the vehicle-induced vibration characteristics of long-span railway cable-stayed bridges, the method of vehicle-bridge coupled vibration was adopted to study the impact effects of different train’s operational conditions on bridges’ local elements. Based on the self-developed software BANSYS, the dynamic responses of long-span railway cable-stayed bridges were calculated, and the effects of train formation, track irregularities, advancing direction and train type on the impact coefficient of each part of a cable-stayed bridge were discussed. The results showed that the same or similar train formation should be adopted when conducting vehicle-bridge dynamic calculations and field dynamic tests; there are obvious differences among the impact coefficients at the same position when the driving direction of train is opposite.
基金项目:浙江省公益性技术应用研究计划项目(2014C31035)
收稿日期:2015-02-25修改稿收到日期:2015-04-23
Influencing factors of impact coefficient for long-span railway cable-stayed bridges
LIYong-le1,BAOYu-long1,DONGShi-fu1,2,ZENGYong-ping3,XIANGHuo-yue1(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China; 2. Hubei Provincial Communication Planning and Design Institute, Wuhan 430051, China;3. China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China)
Key words:long-span railway cable-stayed bridge; vehicle-bridge coupled vibration; impact coefficient; influencing factor; train formation
大跨度铁路斜拉桥跨越能力强,刚度大,易满足高速行车的安全性和舒适性,为大跨度铁路桥梁常用桥型之一。由于规范中对冲击系数的规定主要针对中小跨度桥梁,加之斜拉桥和车辆构造本身、桥梁和车辆系统相互作用关系以及轨道不平顺等因素的影响较复杂,对大跨度铁路桥梁的冲击效应研究缺乏充足的实测数据和系统的理论研究[1-2],故采用车-桥耦合振动的方法,分析各因素对大跨度铁路斜拉桥冲击系数的影响规律,并做出定性的分析具有一定的理论意义。
国内外许多学者对公路桥梁的冲击系数进行了大量的试验研究[3-4],并取得了显著的成果,但对铁路桥梁,尤其是大跨度铁路桥梁冲击系数的研究较为有限。李国豪[5]研究了铁路列车荷载作用下悬索桥的强迫振动问题,成为国内首先研究桥梁冲击系数的学者。朱光汉等[6]通过建立一系悬挂四轴车辆模型,并分析了铁路车桥垂向动力问题,提出单一车辆过桥时桥梁冲击系数大于多节车辆。曹雪芹[7]通过大量的现场实测,并结合相应的理论分析,研究钢桁梁桥车桥振动问题,分析得出桥梁结构冲击系数随车速的提高而增大,但当车速增加至一定值时,冲击系数基本不再增大。然而,前述研究主要针对中小跨度简单桥型的冲击系数,目前国内外相关规范也未对大跨度复杂桥型冲击系数做出相应的规定,业界对大跨度桥梁冲击系数及影响因素的认识较有限,多数仍套用中小跨度的相关规定。此外,已有的针对大跨度斜拉桥冲击系数的实测研究结果差异也较大。
本文以某大跨度铁路斜拉桥为例,建立了相应的有限元模型,采用自主研发的桥梁科研分析软件系统BANSYS[8]进行车-桥耦合动力响应分析,得到了静、动态车辆过桥的时程响应,研究了斜拉桥主梁、斜拉索及支座的冲击系数,并探讨了列车编组、轨道不平顺、行车方向和列车类型等列车运营因素对桥梁冲击效应的影响。
1车-桥耦合振动分析模型
1.1工程概况
该大跨度铁路斜拉桥跨径组合布置为(81+ 135+432+135+81)=864m(见图1),主梁采用板桁结构,具有2片主桁,桁架为N形。桥塔为变截面花瓶型混凝土桥塔,斜拉索采用镀锌高强钢丝索,为平行扇形双索面布置。
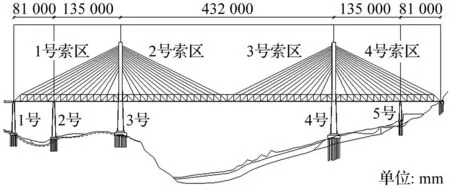
图1 斜拉桥总体布置图(单位:mm) Fig.1 Overall arrangement of cable-stayed bridge(units: mm)
桥梁结构分析模型采用等效格子梁理论,将正交异性桥面板简化为梁格体系。主梁桁架和桥塔各构件均采用空间梁单元模拟,斜拉索采用杆单元模拟,采用正交三梁模型[9]模拟基础刚度,计算得到的桥梁前10阶自振频率和振型见表1。
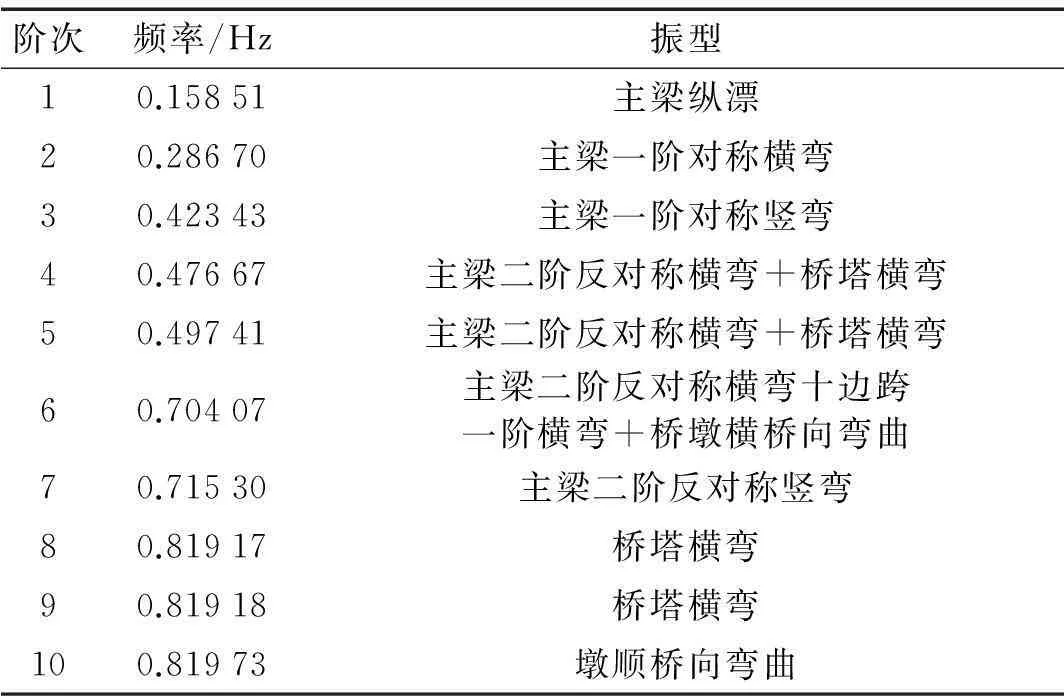
表1 桥梁频率及振型
1.2车-桥耦合振动分析[8]
采用自主开发的桥梁科研分析软件BANSYS(Bridge Analysis System)进行车桥耦合动力响应计算分析。将整个车桥系统分为车辆和桥梁两个子系统,将车辆分为1个车体、2个转向架及4个轮对总共7个刚体23个自由度的二系悬挂的分析模型,桥梁采用有限元法建立分析模型。两者通过建立轮轨接触处的几何位移关系和轮轨之间的相互作用力间的耦合关系相联系,独立求解车辆和桥梁的运动方程,并采用分离迭代法求解系统的耦合响应。首先采用多跨简支梁,验证了运用车-桥耦合振动的方法进行冲击效应分析的可靠性[10]。冲击系数是指移动列车荷载作用下桥梁的动态响应和列车静止作用在桥上的静态响应之比,表示为如下:
(1)
式中,Rdmax,Rsmax分别为列车通过桥梁时响应时程曲线上的最大动力响应值和最大静力响应值;μ为冲击系数。
2列车编组的影响
为考察列车编组对桥梁冲击系数的影响,采用CRH2列车进行一系列车桥耦合振动分析。不同车速下,4种不同列车编组典型工况见表2。

表2 不同列车编组的计算工况
图2为桥梁全跨主梁的不同位置处竖向位移冲击系数。不同车速下竖向位移冲击系数分别见图3和图4。由图2可见,列车编组长度对桥梁冲击系数的影响与桥梁断面位置有关,单独一辆车过桥时,进桥侧左边跨主梁竖向位移冲击系数明显比其他编组要大,且主跨处主梁冲击系数变化幅值较大。由图3和图4可见,4、8、16辆车过桥时,桥梁左边跨跨中竖向位移冲击系数随车速的变化趋势和数值基本一致,但当一辆车通过桥梁时,差别较大,说明单独一辆车过桥和列车车列过桥时桥梁冲击系数有较大的区别,车列对桥梁的动力作用与单独车辆不同,因为车列过桥时车辆之间的激励作用使桥梁动力响应幅值相互叠加减小。斜拉桥主跨跨中处不同列车编组长度下桥梁冲击系数随车速变化趋势相近,说明列车长度对桥梁主跨冲击系数的影响总体上不大,较其对边跨影响要小。
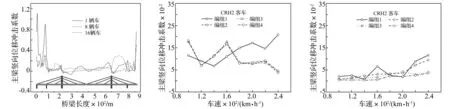

图2 主梁不同位置处竖向位移冲击系数(200km·h-1)Fig.2Impactcoefficientsforverticaldisplacementofmaingirder图3 左边跨跨中冲击系数Fig.3Impactcoefficientsoftheleftsidespan图4 主跨跨中冲击系数Fig.4Impactcoefficientsofthemainspan
为研究编组长度对斜拉索索力冲击系数的影响,将斜拉桥拉索分为四个索区,具体索区位置见图1,各索区斜拉索由短到长依次编号为1~14号。车速为200km/h时不同编组长度下各个索区的拉索冲击系数见图5。不同编组长度下斜拉桥4号索区1号拉索索力冲击系数随车速变化曲线见图6。
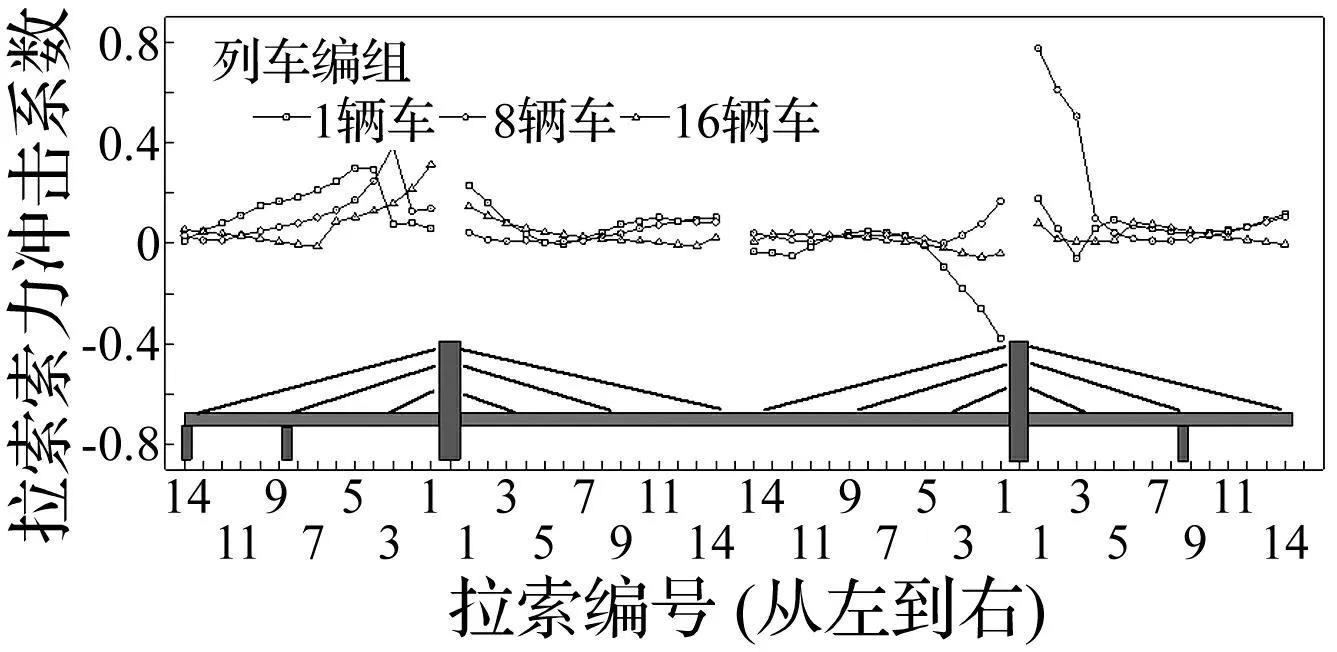
图5 拉索索力冲击系数(从左到右) Fig.5 Impact coefficients for cable force(from left to right)
由图5可见,列车过桥对短索的冲击效应一般比长索较大,这与索的刚度有关,单独车辆过桥时3号索区1号拉索冲击系数达到最小值-0.377,16辆车过桥时4号索区1号拉索冲击系数达到最大值0.774。由图6可以看出,编组1、2、4拉索索力冲击系数随车速的变化趋势大致相同,编组3拉索冲击系数随车速变化趋势和其他三种编组有一定的差异。1辆车和4辆车过桥时拉索冲击系数较为接近。单独一辆车过桥和列车车列过桥时拉索冲击系数有较大的区别,车列对拉索的动力作用与单独车辆不同。
为研究支座内力冲击系数变化分布,将斜拉桥桥墩从左到右依次编号为1-5号,见图1,其中每个桥墩各有左右两个支座,下同。当列车以不同编组长度以200km/h的速度从桥梁左侧加载过桥时,支座的内力冲击系数见图7。由图7可知,单独车辆过桥时,进桥侧桥墩支座内力冲击系数明显比其他编组要大,可达到0.81。


图6 1号拉索索力冲击系数Fig.6ImpactcoefficientsofforceforNo.1cable图7 不同编组下支座内力冲击系数Fig.7Impactcoefficientsofbearings图8 主梁不同位置处竖向位移冲击系数(200km/h)Fig.8Impactcoefficientsforverticaldisplacementofmaingirder
3轨道不平顺的影响
为研究轨道不平顺的影响,选取CRH2客车,编组为:2×(1拖+1动+1动+1拖),分别进行不考虑轨道不平顺、郑武线实测轨道不平顺、美国六级谱不平顺三种情况下的车桥动力响应分析。200km/h车速下桥梁全跨主梁的不同位置处竖向位移冲击系数见图8,其中不同车速时各轨道不平顺情况下左边跨跨中及主跨跨中竖向位移冲击系数分别见图9和图10。
由图8可见,三类轨道不平顺下大跨度斜拉桥的主梁竖向位移冲击系数基本相同,但美国六级谱不平顺时右次边跨主梁竖向位移冲击系数变化幅度很大,可以达到0.298。从图9和图10可以看出,美国六级谱不平顺时,在列车速度超过180km/h后,左边跨跨中桥梁竖向位移冲击系数随车速变化趋势与另两类轨道不平顺有所差异,这是由于时美国六级谱引起的车体加速度响应较大,从而影响桥梁的动力响应。考虑轨道不平顺和不考虑轨道不平顺对主跨跨中位移冲击系数影响不大,在不同轨道不平顺下动力响应差别不大。
不同轨道不平顺下4号索区1号拉索索力冲击系数随车速变化曲线见图11。车速200km/h时不同轨道不平顺下支座内力冲击系数见图12。
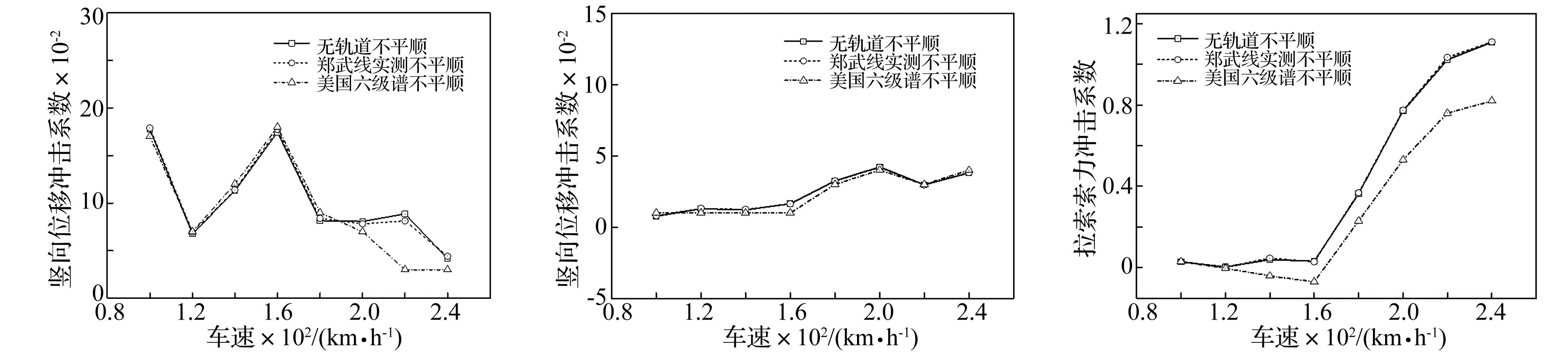

图9 左边跨跨中冲击系数Fig.9Impactcoefficientsoftheleftsidespan图10 主跨跨中冲击系数Fig.10Impactcoefficientsofthemainspan图11 1号拉索索力冲击系数随车速变化曲线Fig.11ImpactcoefficientsofforceforNo.1cable
从图11可以看出,拉索索力冲击系数在不考虑轨道不平顺和采用郑武线实测轨道不平顺两种情况下基本一致,但采用美国六级谱时冲击系数较小,说明郑武线轨道不平顺和不考虑轨道不平顺对拉索索力冲击系数影响很小,高干谱对拉索索力冲击系数影响较大。由图12可知,三种轨道不平顺下支座内力冲击系数基本一致。这表明轨道不平顺对斜拉桥各局部构件的冲击系数影响程度不一样,对主梁和拉索的影响要大于对支座的影响,且与其引起的车桥耦合振动响应有关。
4行车方向的影响
列车以不同的行车方向运行时,尤其是当桥梁结构不对称时,列车荷载对桥梁结构在同一位置的激励会不同,从而使同一位置的桥梁构件处在列车以不同行车方向运行时的冲击效应也不相同。为分析列车行车方向对桥梁冲击系数的影响,选取CRH2客车,编组为:2×(1拖+1动+1动+1拖),轨道不平顺为郑武线实测不平顺,对以下两个工况的计算分析:①列车由左向右行驶;②列车由右向左行驶。200km/h车速下桥梁全跨主梁的不同位置处竖向位移冲击系数见图13, 不同行车方向下桥梁左边跨和主跨跨中位移冲击系数随车速的变化曲线见图14和图15。
由图13可以看出,同一主梁断面位置处竖向位移冲击系数在不同行车方向下有左右对称形式。由于本桥桥梁结构左右不完全对称,冲击系数不完全相对于主跨跨中左右对称,说明主梁同一位置处竖向位移冲击系数与行车方向有很大关系。从图14和图15可以看出,不同行车方向下桥梁边跨跨中位移冲击系数随车速的变化趋势大致相同,但冲击系数数值差别较大。桥梁主跨跨中处位移冲击系数在不同的行车方向下两者基本相同,说明行车方向对桥梁主跨跨中的位移冲击系数影响很小。

图12 不同轨道不平顺下支座内力冲击系数Fig.12Impactcoefficientsofbearings图13 主梁不同位置处竖向位移冲击系数(200km/h)Fig.13Impactcoefficientsforverticaldisplacementofmaingirder图14 左边跨跨中冲击系数Fig.14Impactcoefficientsoftheleftsidespan
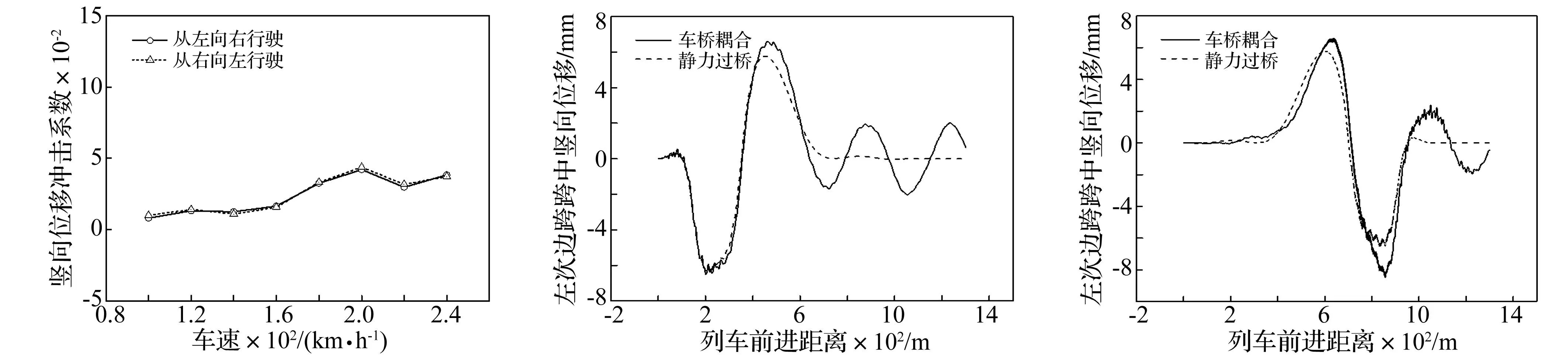

图15 主跨跨中冲击系数Fig.15Impactcoefficientsofthemainspan图16 左次边跨竖向位移时程图(从左到右行驶)Fig.16Timehistoryofverticaldisplacementoftheleftsecondsidespan图17 左次边跨竖向位移时程图(从右到左行驶)Fig.17Timehistoryofverticaldisplacementoftheleftsecondsidespan
图16和17分别为车速200km/h时不同行车方向下左次边跨跨中竖向位移时程图。由图可知,不同行车方向下主梁上同一点的最大位移响应值不同,故冲击效应差别较大。这表明,同一位置处的主梁竖向位移冲击系数具有方向性,现场动力试验应考虑两种不同的行车方向。
不同行车方向下4号索区1号拉索索力冲击系数随车速变化曲线见图18。车速200km/h时不同行车方向下支座内力冲击系数见图19。
从图18可以看出,不同行车方向下拉索索力冲击系数随车速的变化趋势不同,列车以不同行车方向通过时同一拉索拉索索力冲击系数相差较大,特别是在高车速下,行车方向对拉索索力冲击系数的影响明显。由图19可见,不同行车方向对支座冲击系数影响较大,1号桥墩右侧支座冲击系数在不同行车方向下变化可达到0.23。
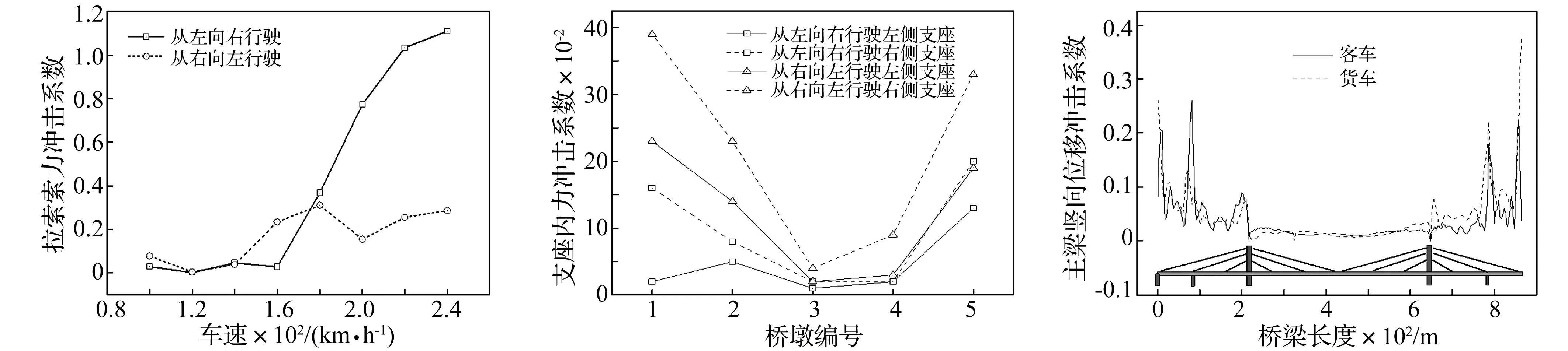

图18 1号拉索索力冲击系数随车速变化曲线Fig.18ImpactcoefficientsofforceforNo.1cable图19 不同行车方向下支座内力冲击系数Fig.19Impactcoefficientsofbearings图20主梁不同位置处竖向位移冲击系数(120km/h)Fig.20Impactcoefficientsforverticaldisplacementofmaingirder
5列车类型的影响
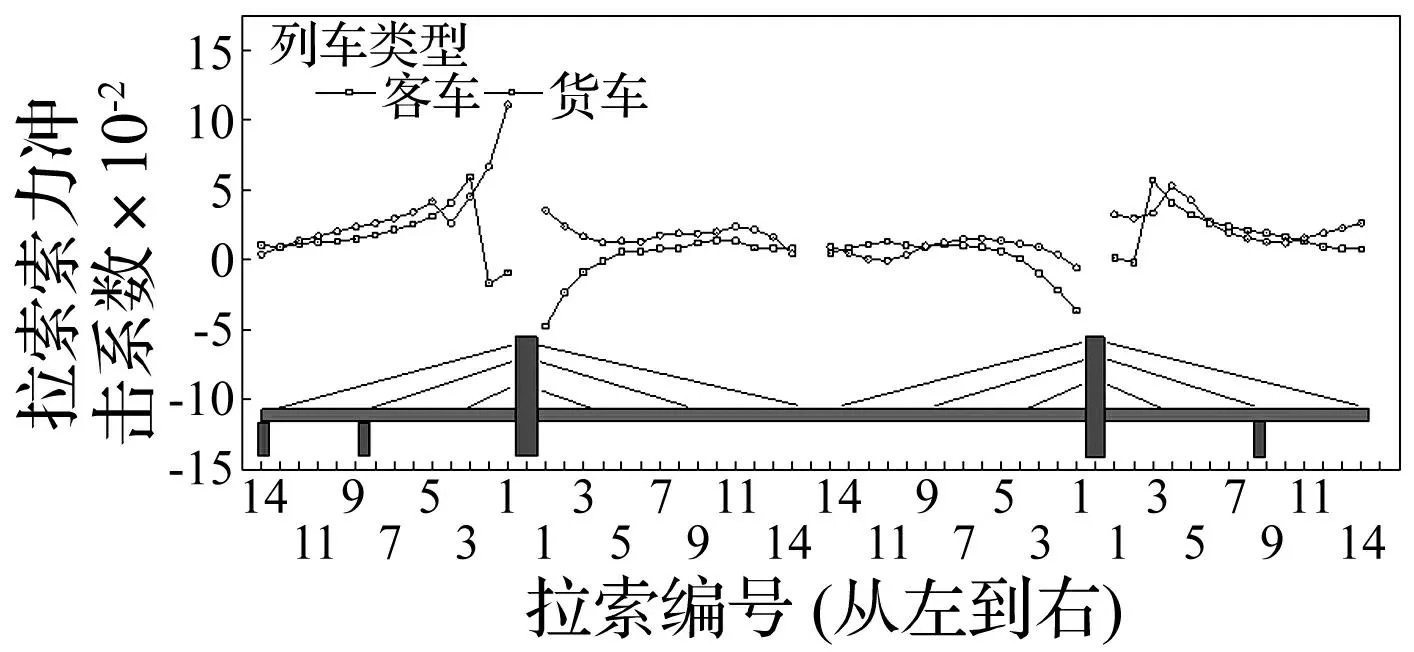
图21 拉索索力冲击系数(从左到右) Fig.21 Impact coefficients for cable force(from left to right)
为分析不同列车类型对桥梁冲击系数的影响,选取以下两个工况进行车桥耦合计算分析:①C80货车,列车编组为:1动+20拖;②CRH2客车,列车编组为:2×(1拖+1动+1动+1拖)。行车速度均为120km/h,轨道不平顺为郑武线实测不平顺。桥梁全跨主梁的不同位置处竖向位移冲击系数见图20, 不同列车类型下各个索区的拉索冲击系数见图21,不同列车类型下支座内力冲击系数见图22。
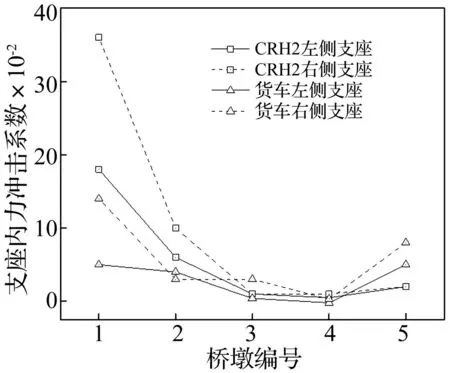
图22 不同列车类型下支座内力冲击系数 Fig.22 Impact coefficients of bearings
由图18可以看出,两种类型的列车通过桥梁时,主梁上竖向位移冲击系数变化趋势基本一致,但桥墩及桥塔附近断面的主梁竖向位移冲击系数相差较大。从图19和图20可以看出,总体上说客车的拉索索力冲击系数比货车要大,且客车的支座内力冲击系数明显比货车大很多。
6结论
(1)大跨度铁路斜拉桥列车编组长度对桥梁主梁竖向位移冲击系数的影响与桥梁断面位置有关,不同编组长度对边跨及次边跨影响较主跨更大。单独车辆或少量车辆过桥时桥梁主梁和支座冲击效应较整列车过桥时更显著,进行车桥动力计算和动力试验时,应尽量采用与实际列车相同或相似的列车编组。
(2)轨道不平顺对大跨度铁路斜拉桥冲击系数的影响与其产生车桥耦合作用响应的大小有关。当轨道不平顺引起的车辆动力响应较大时,会对桥梁局部构件冲击效应产生较大影响。轨道不平顺对主梁和拉索冲击系数的影响要大于对支座的影响。
(3)行车方向对大跨度铁路斜拉桥主梁竖向位移冲击系数影响较大,冲击效应的总体趋势基本相同,且以主跨跨中为中心左右具有一定的对称性。但同一位置处的构件冲击系数具有方向性,现场动力试验时要考虑不同行车方向的影响。
(4)列车类型不同,对桥墩及桥塔附近主梁竖向位移冲击系数影响较大,对主跨冲击系数影响较小。
参考文献
[1]项海帆,吴定俊. 我国铁路桥梁的现状和展望[J]. 2001, (2):1-5.
XIANG Hai-fang, WU Ding-jin. The present situation and prospect of railway bridge in china[J]. Railway Construction Technology, 2001, (2):1-5.
[2]许慰平,程庆国. 大跨度铁路桥梁车桥耦合振动研究[J]. 中国铁道科学,1989, 10(2): 14-26.
XU Wei-ping, CHENG Qing-guo. Study on space dynamic interaction between train and long-span railway bridge[J]. China Railway Science, 1989, 10(2):14-16.
[3]王永平,陈彦江,傅金科. 单车荷载下简支梁桥的动力特性和响应的试验研究[J]. 土木工程学报,1995, 28(5): 39-47.
WANG Yong-ping, CHEN Yan-jiang, FU Jin-ke. Experimental and theoretical analysis of dynamic characteristics and response of highway bridge under single moving vehicle[J]. China Civil Engineering Journal, 1995, 28(5): 39-47.
[4]周勇军,赵煜,贺全海,等. 刚构-连续组合桥梁冲击系数多因素灵敏度分析[J]. 振动与冲击,2012, 31(3): 97-101.
ZHOU Yong-jun, ZHAO Yu, HE Quan-hai, et al. Muti-parameters sensitivity analysis of impact factors for rigid-continious conbined bridge[J]. Journal of Vibration and Shock, 2012, 31(3): 97-101.
[5]Li K H. Lotrechte Schwingungen der Hangebrucken Ingenieur-Archiv Ⅷ,1942.
[6]Chu K H,Garg V K. Railway-bridge impact: simplified train and bridge model[C]//Structural Division, ASCE. 1979, 105(ST9).
[7]曹雪芹. 车速提高至140km/h对既有桥跨结构的影响分析[J]. 铁道学报,1991, 13(3): 97-104.
CAO Xue-qin. Dynamic response of the bridge structure under high-speed train loads[J]. Joural of the China Railway Society, 1991, 13(3): 97-104.
[8]李永乐,强士中,廖海黎. 风-车-桥系统空间耦合振动研究[J]. 土木工程学报,2005,38(7):61-64.
LI Yong-le, QIANG Shi-zhong, LIAO Hai-li. 3-D coupled vibration of wind-vehicle-bridge system [J]. China Civil Engineering Journal, 2005, 38(7): 61-64.
[9]李永乐,赵凯,蔡宪棠. 桥梁基础刚度有限元模拟的正交三梁模型[J]. 桥梁建设,2010(6): 17-20.
LI Yong-le, ZHAO Kai,CAI Xian-tang. Three-orthogonal-beam model for finite element simulation of bridge foundation stiffness[J]. Bridge Construction, 2010(6): 17-20.
[10]董世赋. 基于车桥耦合振动的铁路桥梁冲击系数研究 [D]. 成都:西南交通大学, 2013.
[11]Au F T K, Wang J J,Cheng Y K. Imapct study of cable-stayed bridges under railway traffic using various models[J]. Journal of Sound and Vibration, 2001, 240: 447-465.
[12]向俊,马长水,曾庆元. 列车编组对桥梁振动响应影响的试验研究[J].实验力学,2002,17(4):504-510.
XIANG Jun, MA Chang-shui, ZENG Qing-yuan. Research on the effect of train formation on bridge vibration responses[J]. Journal of Experimental Mechanics, 2002, 17(4): 504-510.
[13]郭薇薇,夏禾,李慧乐,等. 铁路新型钢-混凝土组合桁架桥在列车作用下的动力响应分析[J]. 振动与冲击,2012, 31(4):128-133.
GUO Wei-wei, XIA He, LI Hui-le, et al. Dynamic analysis of a new type of railway steel-concrete composite trussed bridge under running trains excitation[J]. Journal of Vibration and Shock, 2012, 31(4): 128-133.
[14]王海城,施尚伟.桥梁冲击系数影响因素分析及偏差成因[J]. 重庆交通大学学报:自然科学版,2007,26(5):25-28.
WANG Hai-cheng, SHI Shang-wei. Analysis of bridge impact coefficient influence factor and the deviation formation[J]. Journal of Chongqing Jiaotong University:Natural Science, 2007, 26(5): 25-28.

第一作者巫修海男,博士生,副教授,1977年生
通信作者陈文华男,博士,教授,博士生导师,1963年生

