基于GM-PHD平滑器的检测前跟踪技术∗

朱红鹏,黄 勇,修建娟,关 键

(1.海军航空工程学院电子信息工程系,山东烟台264001; 2.海军航空工程学院信息融合研究所,山东烟台264001)

0 引言

雷达观测下的弱小目标检测和跟踪一直是一个难点和热点问题。在探测远距离目标或在杂波密度比较大的情况下,目标回波信号信噪比比较低,很难实现对目标的准确检测和稳定跟踪。检测前跟踪方法(TBD)是实现雷达弱小目标检测和跟踪的有效方法,基本思想是在作检测决策前,通过在目标轨迹上回波能量的积累来提高信噪比,实现弱小目标检测并回溯提取其运动轨迹。TBD是一种信号处理的思想,需要依赖具体的方法实现。

基于随机有限集理论(RFS)的多目标跟踪方法能有效避免关联计算,直接估计多个目标的状态,在目标数目时变的情况下仍然适用,是一种新兴的、有前景的多目标跟踪方法。2003年,Mahler基于RFS理论提出了概率假设密度滤波器(PHD)[1]。此后,Vo给出了PHD滤波器的两种收敛实现,即序贯蒙特卡洛PHD(SMC-PHD)[2]和高斯混合PHD(GM-PHD)[3]。西安电子科技大学李翠芸等针对多目标跟踪问题提出了一种GMPHD前向后向平滑算法[4],利用量测数据对滤波值进行平滑,提升目标跟踪精度。Nandakumaran等提出了SMC-PHD平滑滤波器[5],通过对前向滤波后的粒子进行一定步数的后向平滑,在牺牲算法运行效率的基础上提升了目标数目和目标状态的估计精度。

将PHD技术运用于TBD领域还处在起步阶段,有很多急需解决的问题。Punithakumar最早将SMC-PHD方法运用到红外图像的多目标TBD问题中[6],实现了未知数目的弱小目标的检测。在此基础上,国防科技大学林再平在TBD问题中引入SMC-PHD平滑滤波器,提升了红外图像中目标估计的精度[7]。针对SMC-PHD-TBD算法估计精度不高的问题,海军航空工程学院关键等又提出了一种RBPF-PHD-TBD的方法,将目标状态空间降维分解,分别用线性和非线性滤波器进行跟踪,提升了算法的估计性能[8]。基于改进的SMCPHD-TBD算法和标准SMC-PHD-TBD算法的优点和粒子滤波的优点一样,对付非线性、非高斯情况比较理想,其缺点也和粒子滤波一样存在粒子退化的问题。另外,SMC实现的方法还存在峰值提取困难的问题。高斯混合(GM)是一种使用起来比较方便的方法,峰值提取在这种方法的模式下实现起来非常容易,而且工程实现相对于粒子滤波方法要简单得多,计算量也比较小[3]。

本文研究了雷达观测下基于GM-PHD的TBD问题,前期研究发现基于GM-PHD的TBD算法在信噪比较低的情况下存在目标数目估计不准确、状态估计精度下降的问题。鉴于此,本文提出了一种基于高斯混合概率假设密度平滑的检测前跟踪算法(SGM-PHD-TBD),首先给出了SGMPHD-TBD算法的目标运动模型和雷达传感器观测模型,在此基础上,本文阐述了SGM-PHD-TBD算法的具体实施步骤。仿真分析表明,该算法在低信噪比条件下能有效提升目标数目和目标位置的估计精度。

1 目标运动模型和观测模型

1.1 目标运动模型

基于高斯混合概率假设密度滤波算法适用于高斯线性的目标运动模型。假设k时刻目标的数目为N k,第p个目标的运动状态为X p(k),则雷达弱小目标运动模型为

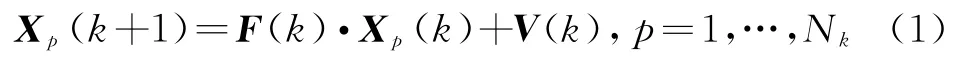
1.2 雷达观测模型

文献[9]建立的雷达观测模型区别于传统的红外观测模型,将回波信号表示为距离-方位多普勒上的三维观测。假设每一扫描周期得到的观测数据大小为Nr×Nd×Nb个分辨单元,其中Nr,Nd和Nb分别表示距离单元、多普勒单元和方位单元数,则k时刻的观测值为

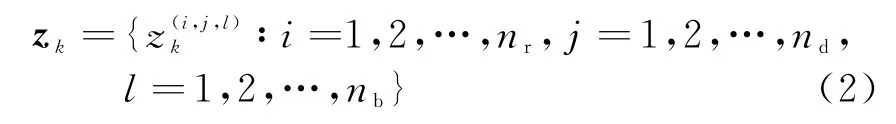
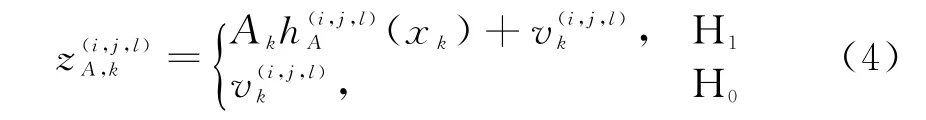
式中,观测噪声v k=vI,k+ivQ,k,vI,k和vQ,k均服从独立的零均值高斯分布,方差均为σ2。分辨单元(i,j,l)处的观测值为

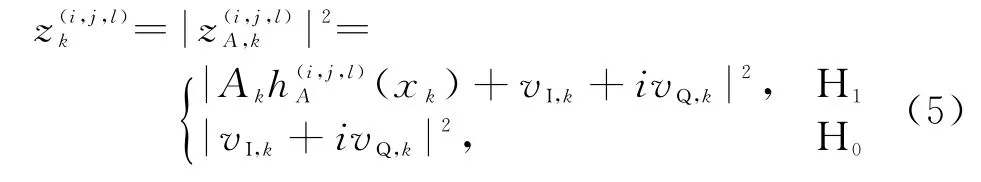
第p个目标在第(i,j,l)个单元内的点扩散函数为

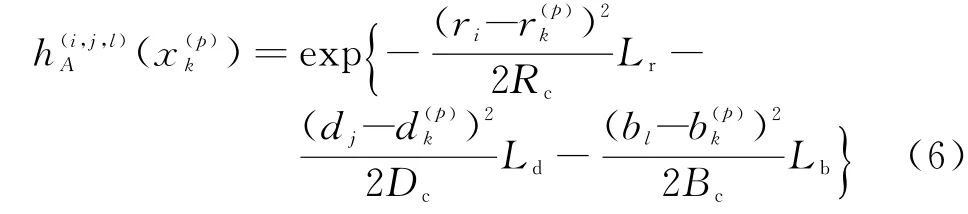
式中:Rc,Dc和Bc表示与距离、多普勒和方位单元尺寸有关的常数,分别根据带宽、积累时间和波束宽度决定;Lr,Ld和Lb分别表示3个观测维度上的损耗系数;r k,d k和b k表示k时刻目标所处的距离、多普勒和方位单元。

由文献[10]可知,针对TBD的“标准”多目标观测模型下的推得的雷达观测似然函数为

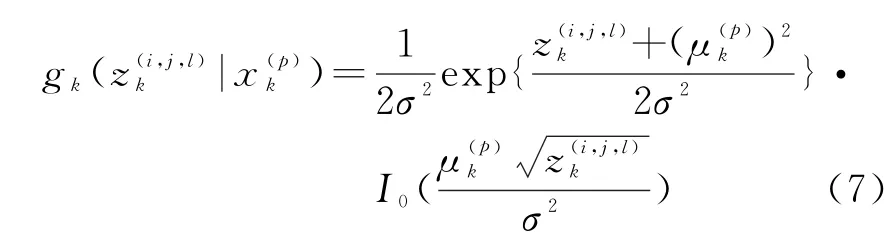
2 SGM-PHD-TBD算法

在线性高斯分布下,当先验分布是混合加权的高斯和形式时,那么更新的后验分布也可以表述成混合高斯的形式。后验密度的估计是通过高斯混合的均值、权值和协方差进行递推得到的。因为高斯分量的个数会随着时间无限增长,所以需要在算法中对描述后验概率密度函数的高斯分量进行处理:通过剪枝操作,去掉权值低的高斯分量;通过合并操作,将分布非常接近的高斯分布合并为一个高斯分量[11]。算法主要步骤如下。

1)初始化

在k=0时刻,定义初始PHD为

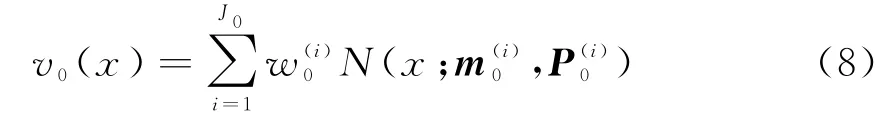
第i个高斯分量具有状态权值均值和方差

2)预测

在不考虑衍生目标的情况下,假设k-1时刻目标的后验概率为以下高斯混合形式:

若vS,k|k-1(x),γk(x)分别表示存活目标和新生目标的强度函数的预测,那么k时刻的目标预测状态的强度函数也是高斯混合的形式:

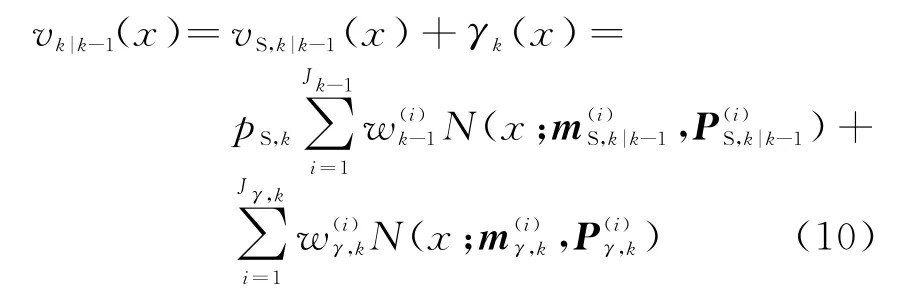
式中,pS,k表示k时刻目标存活的概率,若存活目

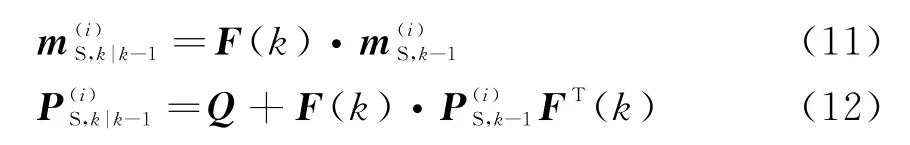
3)更新

假设k时刻的先验概率密度是高斯混合形式,那么k时刻的后验概率密度也是高斯混合的。更新后的后验概率密度v k(x)是由未检测到的项

(1-pD,k)v k|k-1和|Z k|检测到的项vD,k(·;z)组成的,检测的任一项z∈Z k如下:

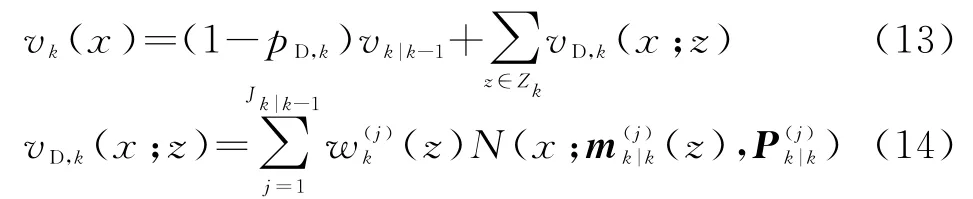
式中,pD,k表示k时刻目标检测的概率。若k时刻杂波的强度函数为κk,量测值为z k,量测噪声协方差为R k,那么高斯分量的权值、均值和协方差的计算公式为

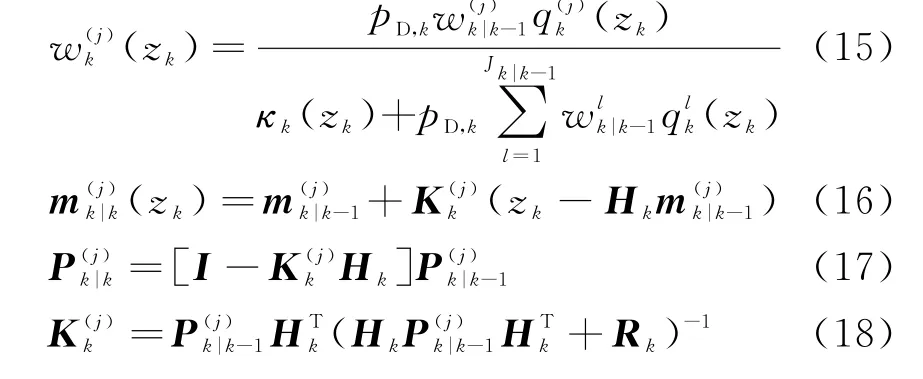
4)平滑

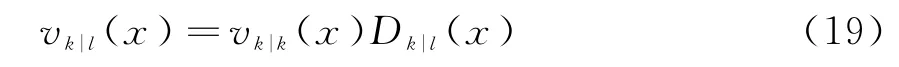
定义在高斯混合假设条件下,D k|l(x)为

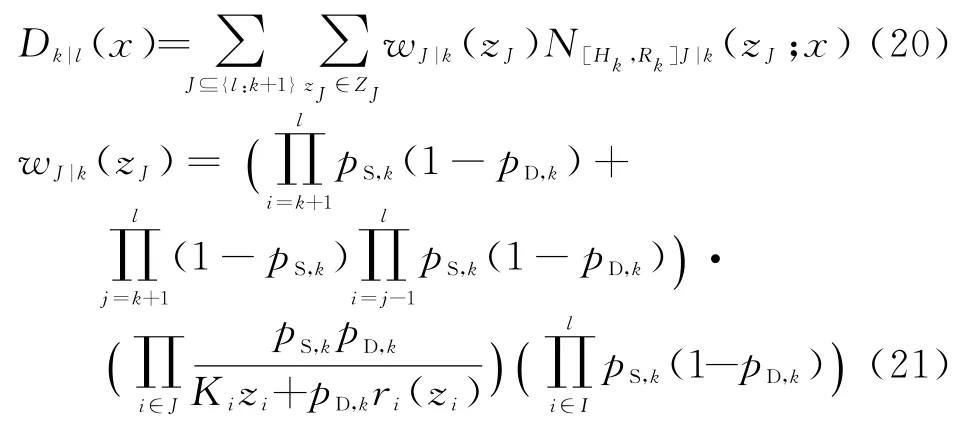
则v k|l(x)为高斯混合形式,表示为

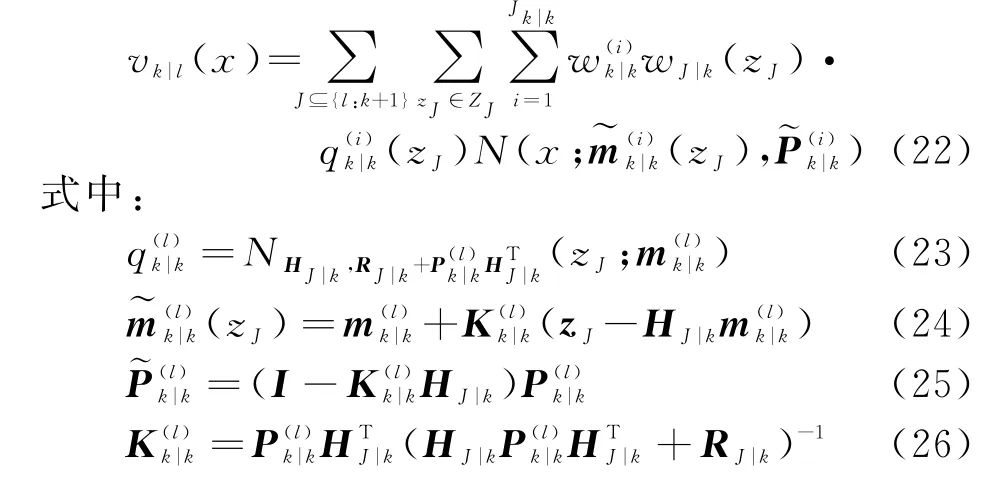
本文采用一阶平滑的算法实现雷达弱小目标的检测前跟踪,即l=k+1,平滑公式为

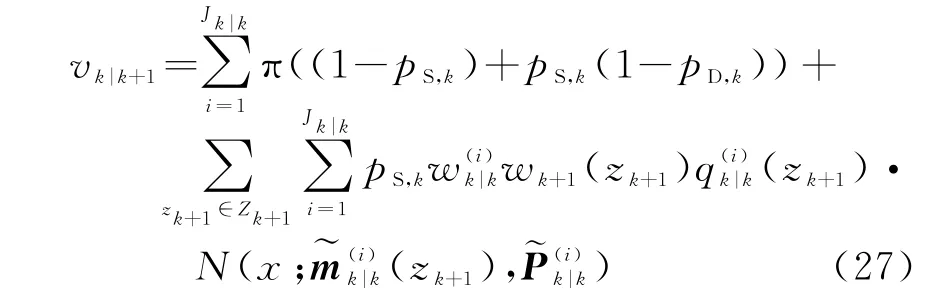
5)合并修剪

在滤波过程中,高斯分量的个数会随着时间无限增长,因此需要对描述后验概率密度函数的高斯分量进行处理:通过剪枝操作去掉权值低的分量;通过合并将分布非常接近的高斯分量直接合并成一个高斯分量。设合并门限为U,若第i个分量和第j个分量的均值满足:

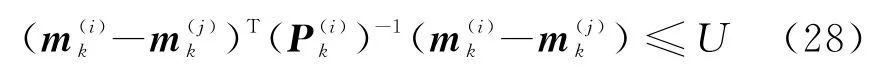
就可以把两者合并成一个分量。合并以后需要进行修剪操作,舍弃权值低于截断阈值T的高斯分量,权值更新后重复步骤2)～步骤5)。

3 仿真与分析

3.1 仿真环境

仿真设置目标的距离单元均匀分布在[0,10 km],多普勒单元随机分布在[-10 m/s, 10 m/s],为了简化计算,方位单元只取一个波位。设置雷达的检测概率pD,k=pD=0.98,杂波密度λc=12.5×10-4m-2。信噪比计算式为SNR=10 lg(P/2σ2),可依据目标功率和信噪比推算背景噪声方差σ2。假设此区域内存在4个目标,目标的幅度是固定的且均为20,目标的存活概率PS,k= PS=0.99,共仿真40帧数据,采样周期T=1 s。目标运动近似为线性运动,运动方程同式(1)。目标运动噪声的功率谱密度q1=0.001,目标初始状态矩阵及存活时间如表1所示。

表1 目标运动状态表

本文分别以目标数目估计标准差和位置最优子模型分配距离(OSPA)作为目标数目和目标状态估计精度的评价标准[12],选取的位置估计OSPA距离参数为c=5,p=2。在目标检测和跟踪问题中,信噪比低于10 dB的目标被称为弱小目标,仿真建立在3种不同的环境下,信噪比分别为9 dB, 8 d B,7 d B。因为一次仿真的随机性较大,所以采用100次蒙特卡洛实验求统计均值的方法来验证算法的性能。

3.2 仿真结果及分析

实验结果如图1～图3所示。

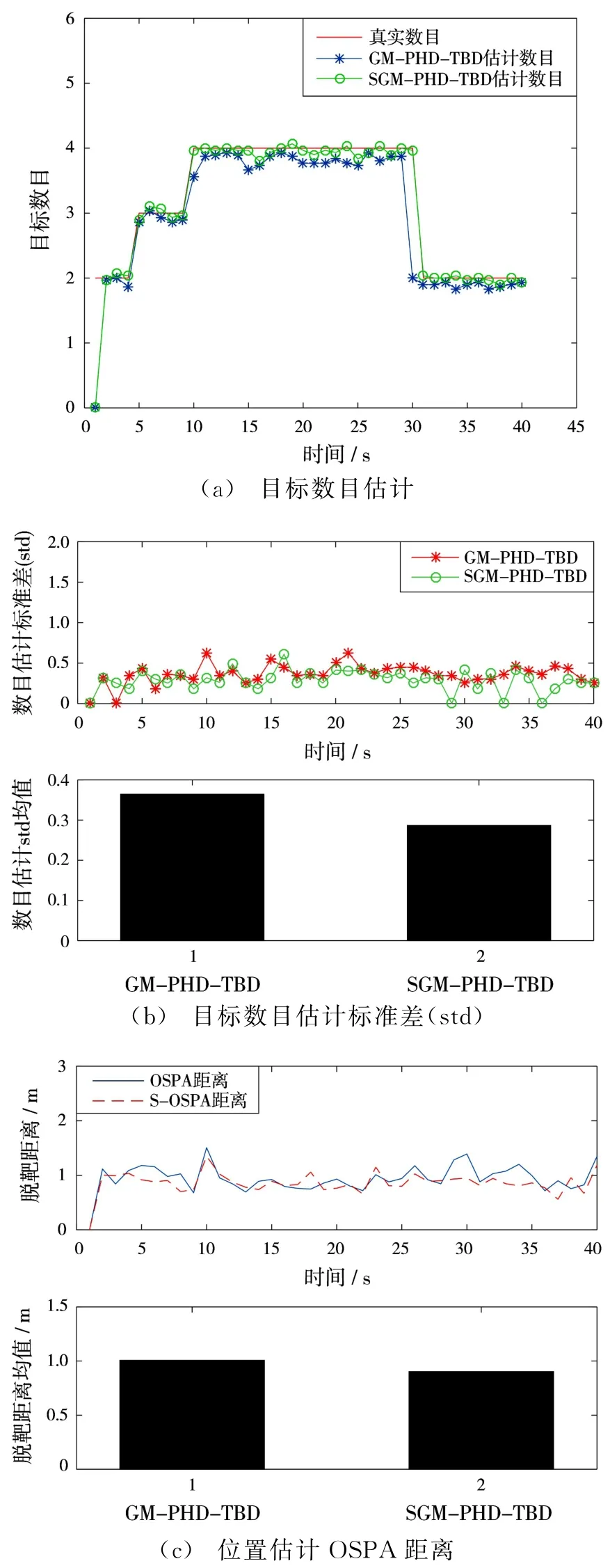
图1 SNR=9 dB两种算法处理效果对比

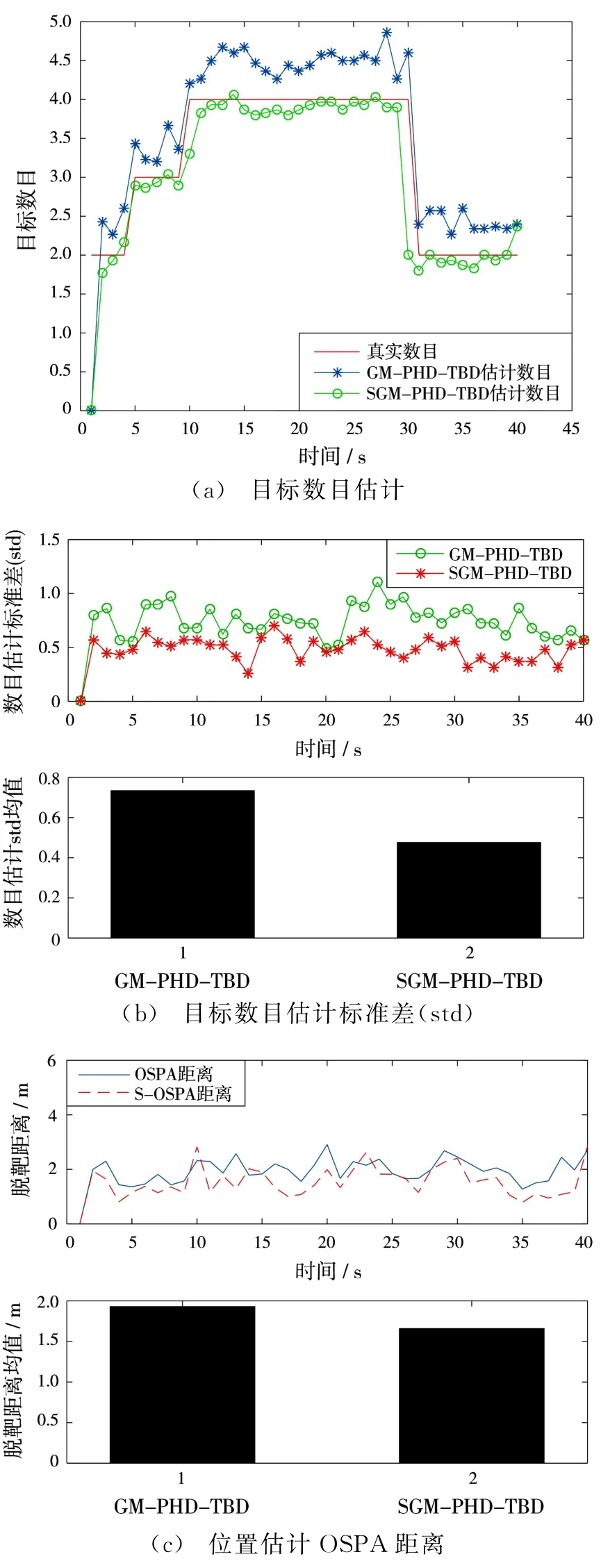
图2 SNR=8 dB两种算法处理效果对比

对比两种算法处理效果,主要从目标数目估计准确度、状态估计精度和算法的运行效率三个方面进行分析。

图3 SNR=7 dB两种算法处理效果对比

在目标数目估计方面。由图1(a)、图2(a)和图3(a)可以看出,两种算法在信噪比较高时对目标数目估计的准确度均较高;随着信噪比的降低,两种算法的准确度均逐步下降,且GM-PHD-TBD算法对目标数目估计的偏差越来越大,而SGMPHD-TBD算法保持了对目标数目良好的估计性能。图1(b)、图2(b)和图3(b)表示的是两种算法100次蒙特卡洛实验目标数目估计的标准差的均值以及40帧数据目标数目估计标准差的均值,统计值越小代表目标数目估计越准确。统计图1(b)、图2(b)和图3(b)中不同信噪比条件下两种算法对目标数目估计的标准差均值,如表2所示。

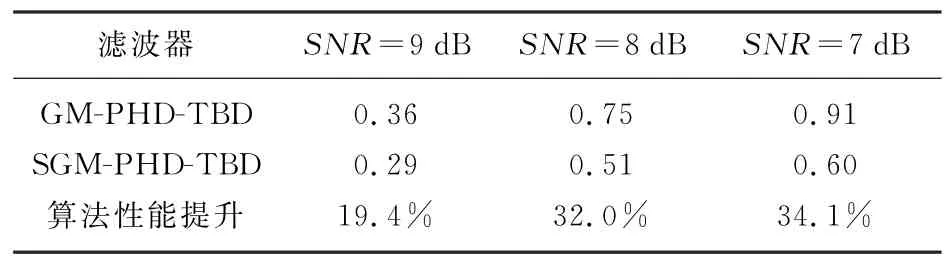
表2 不同SNR条件下两种算法目标数目估计标准差均值

从表2可以看出,SGM-PHD-TBD算法在SNR=9 dB时,相比GM-PHD-TBD算法对目标数目估计的精度可以提升19.4%,在SNR＜9 dB时可以提升30%以上,说明SGM-PHD-TBD算法对弱小目标数目估计更有优势。

在跟踪精度方面。图1(c)、图2(c)和图3(c)表示的是两种算法100次蒙特卡洛实验OSPA均值以及40帧数据OSPA的均值,统计值越小表明目标的状态估计越精确。由图可知,当SNR＜9 d B时,SGM-PHD-TBD算法对目标状态估计明显优于GM-PHD-TBD算法。统计图1(c)、图2(c)和图3(c)不同信噪比条件下两种算法的OSPA误差均值,如表3所示。

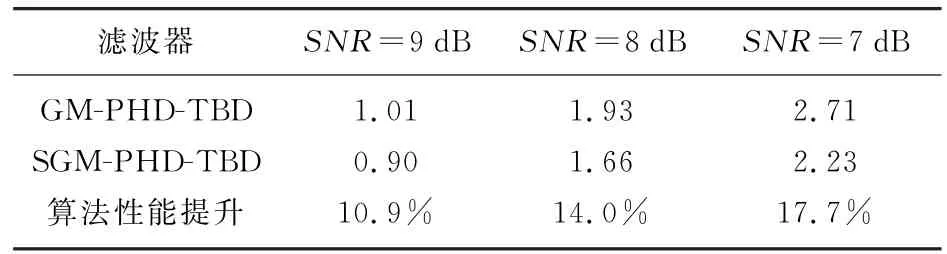
表3 不同SNR条件下两种算法OSPA均值

从表3可以看出,SGM-PHD-TBD算法相比GM-PHD-TBD算法在目标状态的估计精度方面提升了10%以上,且信噪比越低提升的幅度越大,体现出改进算法在低信噪比条件下良好的目标状态估计能力。

在运算效率方面,由于在原方法上引入了平滑滤波器,所以算法的复杂度增加了。统计不同SNR条件下两种算法100次蒙特卡洛实验运算时间均值,如表4所示。

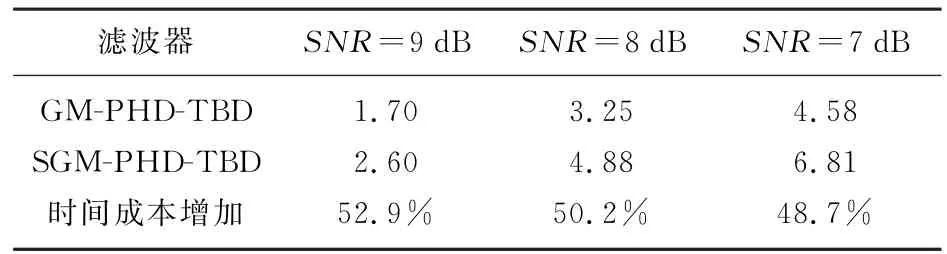
表4 不同SNR条件下两种算法运算时间

从表4可以看出,SGM-PHD-TBD算法相比GM-PHD-TBD算法运行时间增加了50%左右,在对运行时间要求不高的情况下,采用SGMPHD-TBD算法可以更好地实现对雷达弱小目标的检测和跟踪。

4 结束语

本文针对GM-PHD算法在用于TBD过程中存在信噪比降低时目标数目估计不准、目标状态估计精度较低的问题,提出了SGM-PHD-TBD算法,在给出该算法标准运动模型和雷达传感器观测模型基础上,阐述了该算法的具体实施步骤。仿真表明,在不考虑增加时间成本的前提下,SGMPHD-TBD算法相比GM-PHD-TBD算法在低信噪比条件下对目标数目估计的准确度可以提升30%以上,对目标的状态估计的精度可以提升10%以上,能够更好地实现对雷达弱小目标的准确检测和稳定跟踪。

[1]MAHLER R.Multitarget Bayes Filtering via First-Order Multitarget Moments[J].IEEE Trans on Aerospace and Electronics Systems,2003,39(3):1152-1178.

[2]VO B N,MA W K.A Closed-Form Solution for the Probability Hypothesis Density Filter[C]∥8th International Conference on Information Fusion,Philadelphia,PA:IEEE,2005:856-863.

[3]VO B N,MA W K.The Gaussian Mixture Probability Hypothesis Density Filter[J].IEEE Trans on Signal Processing,2006,54(11):4091-4104.

[4]李翠芸,江舟,李斌,等.未知杂波环境的GM-PHD平滑滤波器[J].西安电子科技大学学报(自然科学版), 2015,42(5):98-104.

[5]NANDAKUMARAN N,PUNITHAKUMAR K, KIRUBARAJAN T.Improved Multi-Target Tracking Using Probability Hypothesis Density Smoothing[C]∥SPIE Conference on Signal and Data Processing of Small Targets,San Diego,CA:SPIE,2007: 1-8.

[6]PUNITHAKUMAR K,KIRUBARAJAN T,SINHA A.A Sequential Monte Carlo Probability Hypothesis Density Algorithm for Multitarget Track-Before-Detect[C]∥SPIE Conference on Signal and Data Processing of Small Targets,Bellingham,Washington: SPIE,2005:587-594.

[7]林再平,周一宇,安玮,等.基于概率假设密度滤波平滑器的检测前跟踪算法[J].光学学报,2012,32 (10):1-8.

[8]柳超,关键,黄勇,等.基于PHD的多目标检测前跟踪改进方法[J].雷达科学与技术,2016,14(1):1-6. LIU Chao,GUAN Jian,HUANG Yong,et al.An Improved Multitarget Track-Before Detect Algorithm Based on Probability Hypothesis Density Filter[J]. Radar Science and Technology,2016,14(1):1-6.(in Chinese)

[9]樊孔帅,郭云飞,刘鑫,等.弱目标检测前跟踪快速实现算法及性能分析[J].杭州电子科技大学学报, 2013,33(3):61-64.

[10]童慧思,张颢,孟华平,等.PHD滤波器在多目标检测前跟踪中的应用[J].电子学报,2011,39(9): 2046-2051.

[11]胡玮静,陈秀宏.多目标跟踪中一种改进的高斯混合PHD滤波算法[J].计算机工程与应用,2016,52 (2):244-255.

[12]吴鑫辉,黄高明,高俊,等.未知噪声统计下多模型概率假设密度粒子滤波算法[J].控制与决策,2014, 29(3):475-480.