预警机协同探测拱形任务线阵位配置∗

(空军预警学院,湖北武汉430019)

0 引言

预警机在遂行重点目标防御和空袭作战任务时,由于防空威胁角过大、多目标保护预警线和空袭探测责任区过长等原因,致使单预警机不能有效遂行作战任务,因此需要多预警机协同完成作战赋予的使命任务,其协同模式可分为两种: Model 1——各预警机独立遂行探测任务,目标情报不进行融合处理;Model 2——各预警机情报由指定预警机或上级情报中心进行融合处理。目前, Model 1的多预警机联合探测问题的研究较为深入。文献[1]提出了多预警机并立和串接组合两种空域配置协同探测方案,并对其进行了定量分析,得出在预警机架数有限的前提下,串接航线易造成稳定覆盖区域不稳定,易形成盲区的结论。文献[2]提出了一种基于累积检测概率矩阵2-范数的单机航线优化准则,并讨论了多预警机飞行时间间隔和航线间隔对重点监视区域累积发现概率的影响问题。文献[3]提出了基于作战任务和需求,合理配置预警机巡逻空域,并据此得出预警机兵力使用策略。文献[4]基于雷达干扰自卫距离公式,讨论了有源干扰条件下的多预警机部署优化问题。上述文献均未涉及多预警机信息融合处理。

本文详细分析了两种协同模式的多预警机凸形任务线协同空域配置问题,对任务线、预警机阵位线和等效圆心之间的关系进行了定量描述;运用等概率密度场的方法,对多预警机两种协同方式的可行性进行了定量分析;构建了通用性的多预警机空域配置估算模型。文中构建的各种估算与决策模型考虑了各种主要的内、外因素,具有实用价值。通过仿真,分析了两种模式下多预警机空域配置和资源使用问题,并得出Model 2明显优于Model 1的重要结论。

1 任务线建模

当多架预警机采用并立航线协同遂行目标探测任务时,令各预警机航线中心点E i(i=1,2,…,n)均与阵位线重合,且Oequ和αequ分别为等效圆心和等效扇面角,预警机巡逻直飞航线与过航线中心点的中层防空预警线(责任区远界)半径相垂直,则实时探测区是以直飞航线四端点为圆心、以最大探测距离为半径的交叠区域(图1中阴影区域)[5]。

图1 预警机空域配置态势图

图1(a)、(b)为多预警机协同遂行防御作战任务时的空域配置态势图,图中Od和O j(j=1, 2,…,m)所对应威胁角αd和αj的大小与对方机场和重点目标距离,以及对方战斗机续航能力有关[6-7]。阵位线与中层防空预警线的距离dzh_d和dzh_ft、阵位线与多目标分布线距离Dzy_d和Dzy_ft则与对方战斗机最大平飞速度和续航能力有关。不失一般性,设对方战斗机对于每个重点目标的攻击能力相同,则可用一条与m个重点目标中层防空预警线相切的弧线定量表示防御方整体中层防空预警线。因此,阵位线、中层防空预警线和重点目标分布线均是以Od或Oequ点为圆心,以αd或αequ为扇面角,且按不同距离构筑的弧线,而多架预警机应以近似“橄榄”形的实时探测区对中层防空预警线进行全面覆盖。

图1(c)为多预警机协同遂行空袭作战任务时的空域配置态势图,令任务划定责任区成拱型,Wtc_t为责任区纵深,Dsy_gt为阵位线到责任区近界距离。责任区远界、近界和阵位线均是以Oequ点为圆心,以αequ为扇面角,且按不同距离设置的弧线,因此,此时的“橄榄”形的实时探测区只需对责任区远界进行全面覆盖即可。

令图1(b)、(c)中等效半径|OequO1|和|OequO3|为Requ,等效扇面角为αequ,等效弦长|Q1Q2|和|Q3Q4|为lxc、等效弓高|P1P2|和|P3P4|为hgg,则

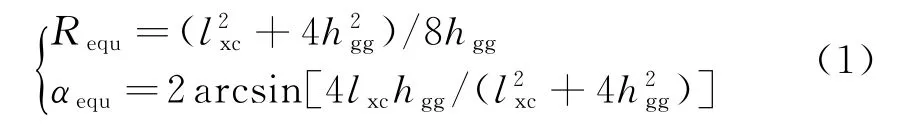
再令圆心到阵位线距离dtx=Dzy_d=Requ-dzh_ft= Requ-Wtc_t,圆心到任务线距离Rtx=dzh_d+Dzy_d= Requ,任务扇面角αtx=αd=αequ,任务线长度ltx= Rtxαtx,则3种预警机作战任务可归结为一类针对凸形任务线实时有效全覆盖时的预警机空域配置问题。

2 协同模式瞬时覆盖区估算

2.1 综合发现概率估算

令预警机有效遂行作战任务所需发现概率为Pd_mis,则两种协同模式时的多预警机综合发现概率Pdcoss的估算公式为

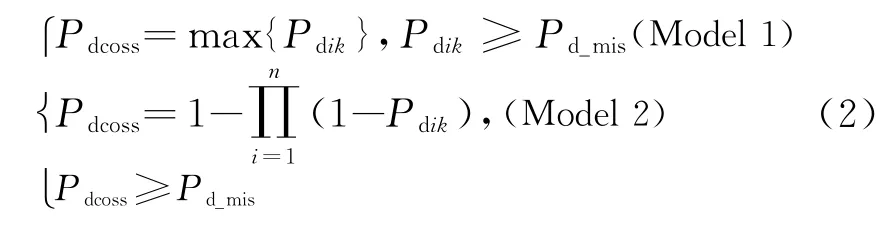
式中,Pdik为第i(i=1,2,…,n)架预警机在距离其k(k=1,2,…,u)点处独立探测目标时的发现概率,令此时预警机探测距离为Rdik。

2.2 遂行不同任务时的实际Rdik估算

防空警戒和对空引导是预警机的两项主要作战任务[8],所需发现概率Pd_mis={0.5,0.8}、虚警概率Pfa=10-6。对于每部机载预警雷达而言,实际Rdik与所探测目标类型有关。对于防空警戒和对空引导两项任务而言,令目标RCS为常量,机载预警雷达最大探测距离Rmaxi,且令第i架预警机在k点处的Rdik=KequikRmaxi,Kequik是发现概率为Pdik时实际探测距离的折算系数,则可根据文献[9]提供的估算方法,构建Pdik与Rdik之间的关系曲线(如图2所示),显然其为单调递减函数。

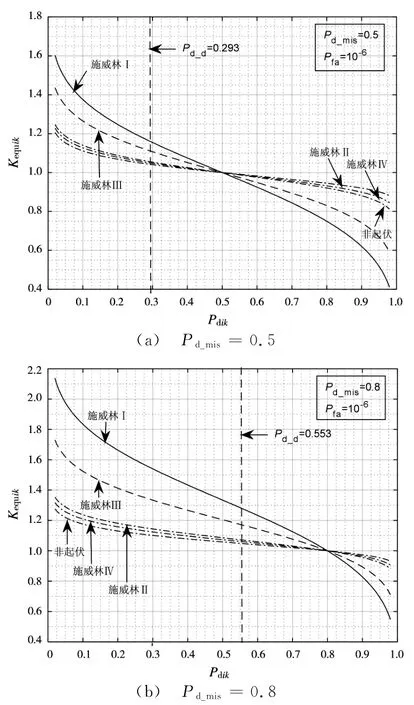
图2Pdik与Kequi的关系

2.3 协同模式瞬时综合覆盖区估算

不失一般性,令任意两架预警机协同工作,则两种协同模式时的综合瞬时覆盖区可按以下流程进行估算:

Step1 获取各预警机在发现概率为Pd_mis时特定目标类型的最大探测距离Rmaxi。

Step2 拟合图2中各具体观测目标类型Pdik与Rdik之间的关系曲线,获得Rdik与Pdik关系式。

Step3Rdik解算:

1)根据式(2)约束条件和图2结论,设定第i-1架预警机发现概率的取值范围为Pdi-1k∈[0,Pd_mis];

2)令Pdcoss=Pd_mis,且根据式(2)两种协同模式方程和Pdi-1k取值范围,解算第i架预警机相应Pdik值;

3)通过Step2解算两种协同模式Pdik和Pdi-1k对应的Rdik和Rdi-1k值。

Step4 设置两架预警机之间瞬时间距dsi-1值,并以i-1架预警机瞬时阵位为坐标原点,以两架预警机瞬时阵位连线为X轴,构建直角坐标系。

Step5 以各预警机瞬时阵位为圆心,以两种协同模式相应Rdik和Rdi-1k为半径,解算各交点坐标。

Step6各交点的连线即为Model1和Model2协同瞬时覆盖区边界。

令相同型号预警机协同遂行作战任务,探测施威林Ⅰ型目标,RCS相同,Pd_mis={0.5,0.8},Pfa=10-6时Rmaxi=1,则Rdik=Kequik,当任意两架预警机ds=1.6Rmax时,其Model1和Model2协同瞬时覆盖区边界如图3所示,F1和F2是两预警机Rdi-1k=Rdik时的交点,其对应图2中Pd_d时Kequik的取值。

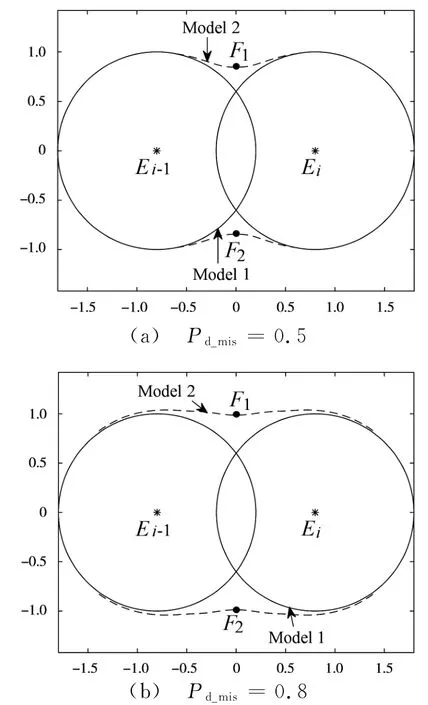
图3 两种协同模式瞬时覆盖区域仿真图

图3中,Model 2协同瞬时覆盖区边界是以各预警机Pdik可降为零的前提条件下绘制的,这在实际中显然不合理。如图4所示,实际预警机机载雷达的脉冲重复周期Tr是一定的,且一般分为3段:tzc段与规定的机载预警雷达的Rmax之间存在对应关系;try段为设计者预留冗余时间,tzc+try称为“工作期”;tfx段为“休止期”,常用于干扰分析和BIT。显然,Model 1可用时间段为tzc,而Model 2可用时间段为tzc+try,因此,Model 2最远可用探测距离Rky=(tzc+try)C/2。令分别以第i-1和第i架预警机瞬时阵位为圆心,相应Rkyi-1和Rkyi为半径的两圆交集面积为

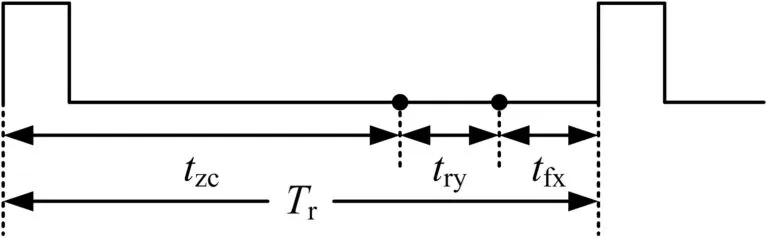
图4 实际预警机机载雷达的脉冲重复周期分配

Ss_crossi-1,相应以Rmaxi-1和Rmaxi为半径的圆面积分别为Ssi-1和Ssi,当Pdik可降为零时Model 2瞬时覆盖区面积为SModel2i-1,则相邻两架预警机不同协同方式时的瞬时覆盖区为

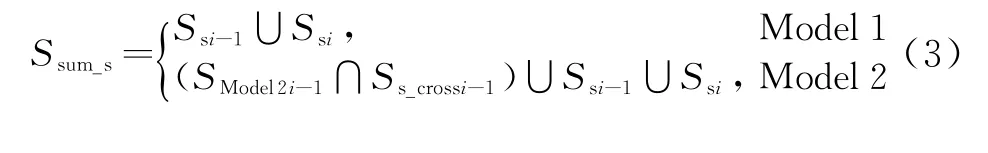
3 空域配置建模

令多预警机协同遂行对空警戒任务,且针对不同重点探测目标类型时,任意一架预警机所用工作方式的Rkyi均不大于图2中Pd_d所对应的Rdik取值。如图5所示,第i架预警机巡逻直飞航线4个端点分别为AYi,BYi,CYi和DYi,且直飞航线长度|AYi BYi|=|CYi DYi|=LYi=2a i,转弯直径|AYiCYi|=|BYi DYi|=WYi=2b i。当多预警机对任务扇面角αtx遂行作战任务时,其协同探测相交边界均是由CYi点和DYi+1点为圆心,Rmaxi、Rkyi和Rmaxi+1、Rkyi+1为半径的圆形构筑,两种协同模式均以E i-1为坐标系原点,Y轴垂直于预警机巡逻直飞航线,构建XE i-1Y直角坐标系。对于Model 1而言,多预警机协同空域配置态势如图5(a)所示,U1是以DYi-1为圆心、以Rmaxi-1为半径的实时探测边界和任务线的交点,U2是分别以CYi-1、DYi为圆心,以Rmaxi-1、Rmax为半径的实时探测边界交点,且与任务线重合,则∠U1OU2=ωti-1,∠E i-1OE i= γti-1,显然|OU1|=|OU2|=Rtx,|OE i-1|=|OE i|= dtx,联立方程组:

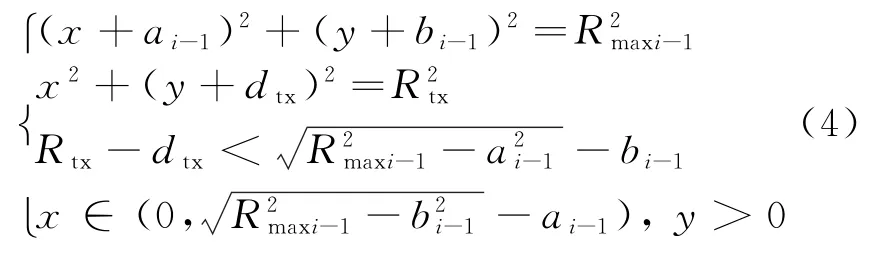
可求得U2坐标为(x U2,y U2),则第i-1架预警机单独覆盖任务线对应O点角度ωti-1,以及第i-1架与第i架预警机之间空域配置角γti-1为

因此,当任务扇面角为αtx时,所需预警机同时出动架数n的约束条件为

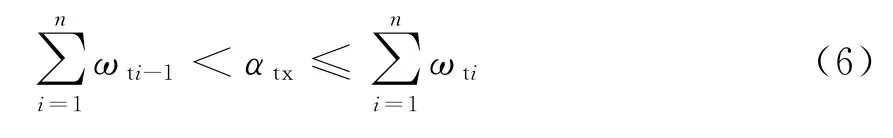
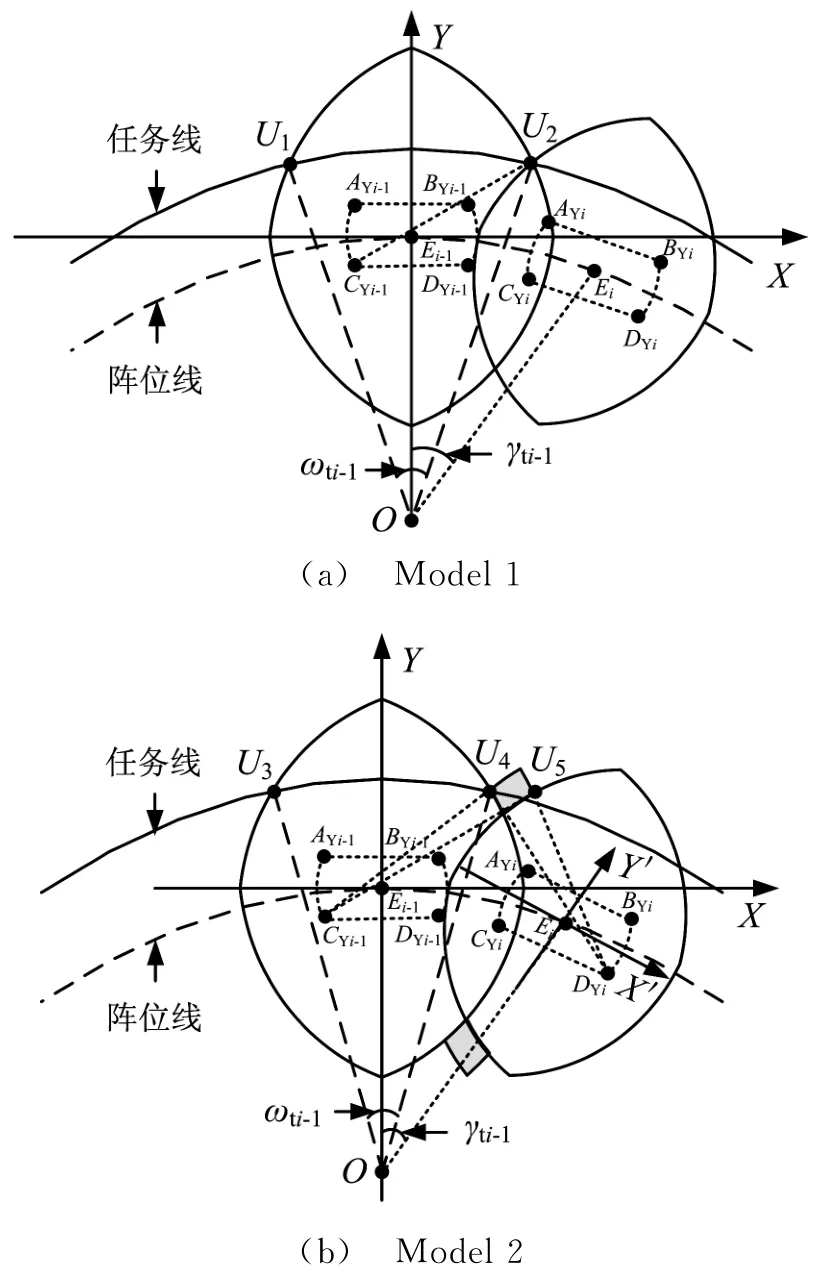
图5 多预警机拱形任务线协同覆盖示意图

对于Model 2而言,多预警机协同空域配置态势如图5(b)所示,U3是以DYi-1为圆心、以Rmaxi-1为半径的实时探测边界和任务线的交点,U4是分别以CYi-1、DYi为圆心,以Rmaxi-1、Rkyi为半径的实时探测边界的交点,U5是分别以CYi-1、DYi为圆心,以Rkyi-1、Rmaxi为半径的实时探测边界的交点,∠U3OU4=ωti-1与Model 1中∠U1OU2相同,∠E i-1OE i=γti-1。令DYi在坐标系XE i-1Y下的坐标为(p i,q i),以E i为坐标原点,巡逻直飞航线的垂直平分线为Y′轴,构建X′E i Y′直角坐标系,将坐标系X′E i Y′下坐标(x′,y′)逆时针旋转并平移到坐标系XE i-1Y下坐标(x,y)的转换公式为

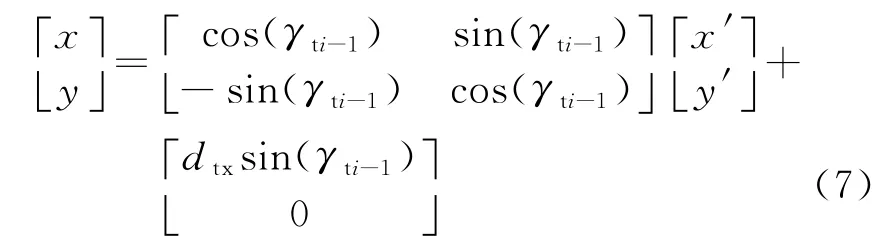
则p i、q i值为

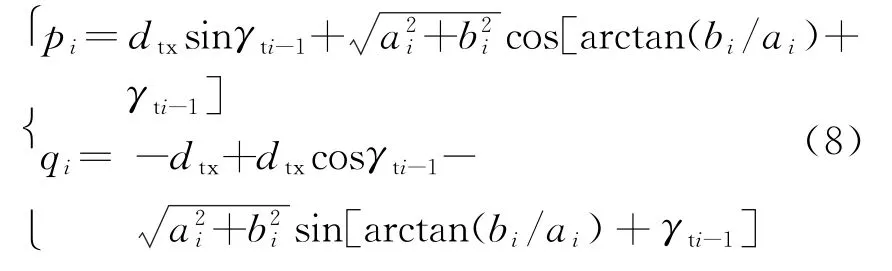
因CYi-1在坐标系XE i-1Y下坐标为(-a i-1,-b i-1),联立方程组:可求得U4坐标为(x U4,y U4)。

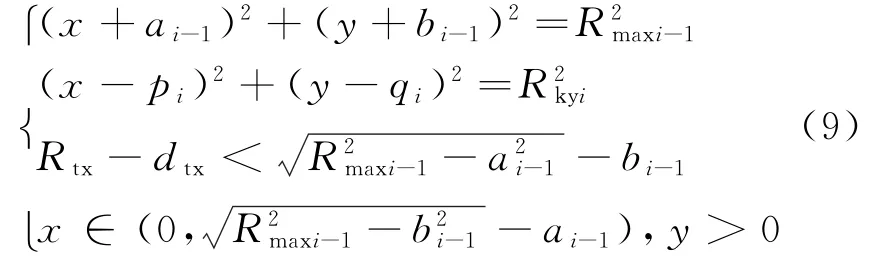
在XE i-1Y坐标系下联立方程组:

可求得U5坐标为(x U5,y U5)。

令|OU4|和|O U5|均为Rtx,则可构建方程:

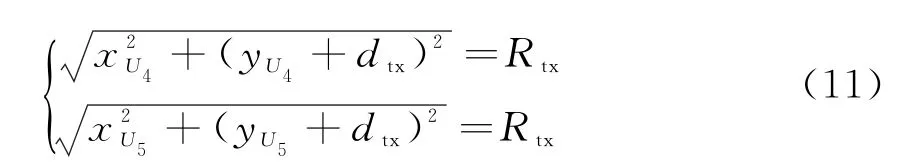
从而求得|OU4|和|OU5|分别对应的γti-1,1和γti-1,2,由于任务线需被预警机实时全覆盖,因此第i-1架与第i架预警机之间空域配置角γti-1=min{γti-1,1,γti-1,2}。

当任务扇面角为αtx时,所需预警机同时出动架数n的约束条件为

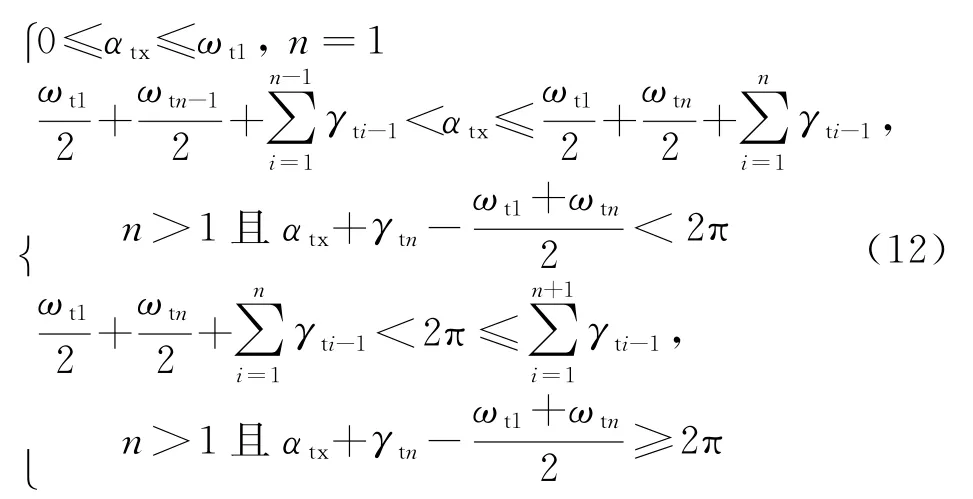
4 仿真分析

4.1 阵位对比分析

为便于分析两种协同模式的差别,令相同型号预警机遂行对空警戒作战任务,且巡逻直飞航线LY为80 km,转弯直径WY为20 km,圆心到任务线距离Rtx=600 km,圆心到阵位线距离dtx∈[300 km,600 km]。不失一般性,当Pd=0.5、Pfa=10-6,且预警机对雷达有效截面为2 m2的施威林I型目标进行探测时,Rky/Rmax=1.16(Kequik=1.161)。则dtx与两种协同模式下相邻两架预警机阵位角γt的关系曲线如图6所示,则可得出以下结论。

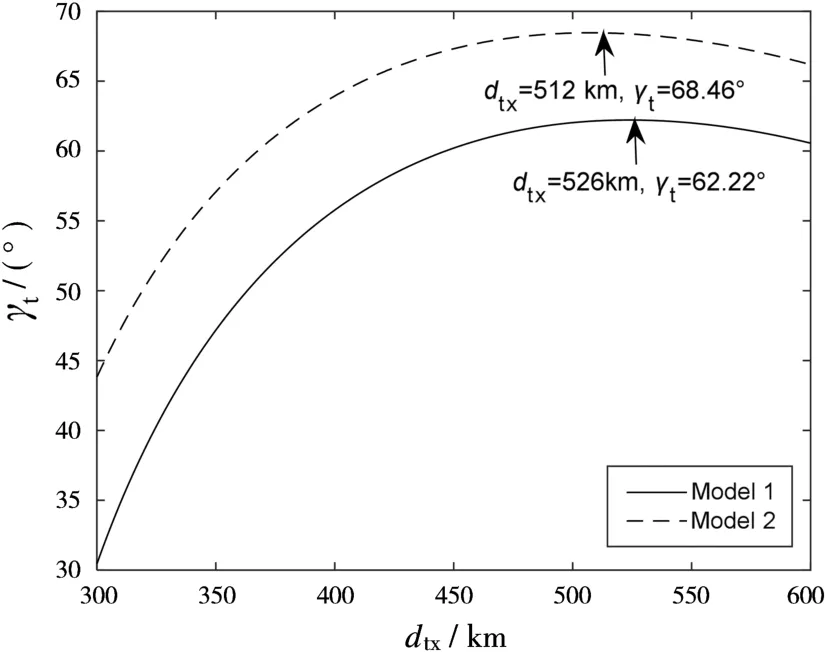
图6 dtx与γt的关系曲线

1)在多预警机协同探测能力范围内,不论dtx取何值,Model 2比Model 1的γt角均大,说明相同战场环境下,使用Model 2协同方式比使用Model 1协同方式可覆盖更长的任务线;

2)分别使用Model 1和Model 2协同方式,在dtx为526 km和512 km时γt均达到最大值,其原因是此时任务线被预警机协同实时探测区横向最宽处所覆盖。

令相同dtx时,Model 2与Model 1的γt角差值为γcz_t,则dtx与γcz_t的关系曲线如图7所示,γcz_t随dtx的增加而减小,说明预警机阵位线越靠近任务线,使用Model 2比使用Model 1协同方式的优势越小。

图7 dtx与γcz_t的关系曲线

4.2 αtx与n取值关系分析

令dtx=370 km,任务扇面角αtx∈[0°,360°],战场环境和预警机固有探测能力及巡逻航线均与上面相同,则所需同时升空预警机架数n与αtx的关系如图8所示,由此可得出以下结论:

1)单架预警机覆盖αtx角度为51.3°,说明当αtx≤51.3°时,预警机无需任何协同方式,单架独立作战即可有效遂行对空警戒任务;

2)当同时升空两架预警机时,分别使用Model 1和Model 2进行协同,其覆盖αtx角度分别为102.6°和111.6°,说明在102.6°＜αtx≤111.6°时,Model 2比Model 1即可节约一架同时升空的预警机资源;

3)随αtx变大,Model 2比Model 1节约预警机资源效果越明显;

4)在292.7°＜αtx≤360°时,Model 2增加第6架预警机对αtx角的覆盖范围均大于之前每增加一架时αtx的增大范围,其原因是此时第6架预警机与第1架预警机之间已可通过相互协同有效遂行作战任务。

5 结束语

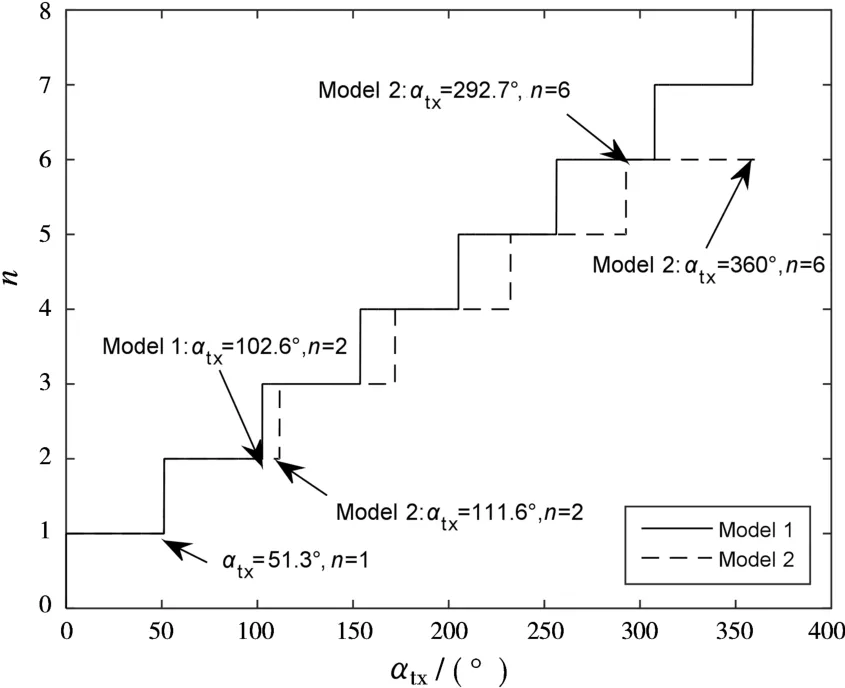
图8 αtx与n的关系曲线

本文针对凸形任务线多预警协同空域配置问题,提出两种协同模式,并通过构建其瞬时覆盖区估算模型,对Model 1和Model 2的空域配置进行定量描述,所建模型考虑了各种主要的内、外因素。通过仿真,分析了两种协同方式时相邻两架预警机阵位角与关键参数之间的关系,并得出在多预警机协同作战资源使用方面, Model 2明显优于Model 1的结论。文中提出的空域配置原则、定量模型,以及仿真结论可供实际预警机兵力部署决策时参考使用。由于篇幅有限,本文未涉及拱形任务线和直线形任务线时多预警机协同空域配置问题,而这些问题有待进行专题研究。

[1]刘波,陈春晖,沈齐.机载预警雷达协同探测航线模式研究[J].现代雷达,2012,34(6):1-4.

[2]付莹,汤子跃,孙永健.机载预警雷达协同探测航线优化[J].红外与激光工程,2014,43(12):4177-4185.

[3]陈云翔,张毅,庄骏,等.基于作战方向的预警机需求确定方法[J].火力与指挥控制,2014,39(8):94-97.

[4]王国师,李强,钱琼芬,等.有源干扰条件下多预警机空中部署及优化[J].红外与激光工程,2012,41 (11):2973-2980.

[5]刘波,沈齐,李文清.空基预警探测系统[M].北京:国防工业出版社,2012:211-215.

[6]程子光,王洪林,姜礼平,等.大型海上编队空中威胁扇面角定量研究[J].空军雷达学院学报,2012,26 (3):195-198.

[7]冯威,王平,许小明.航母编队可能受到的敌空袭威胁扇面大小确定方法研究[J].舰船电子工程,2010,30 (12):61-62.