雷达镜反射模型选择∗

(国防科技大学电子信息系统复杂电磁环境效应国家重点实验室,湖南长沙410073)

0 引言

多径散射作为一种特殊的空间两点源干扰,严重影响着雷达低空目标探测性能,从而备受关注[1-5]。雷达镜反射是影响雷达低空目标探测的重要因素。镜反射模型有两种:一种是一路反射模型[6],另一种是三路反射模型[7]。选用合适的镜反射模型是分析镜反射对雷达检测与跟踪性能影响效果,以及研究镜反射下雷达检测与跟踪技术的基础。

目前,针对雷达检测、跟踪环节,采用哪种镜反射模型较为准确尚未见具体结论。美国著名雷达专家Barton早期研究雷达低仰角跟踪问题时,对镜反射建模采用了一路反射模型[6];文献[8]在分析镜反射对雷达检测性能影响时也采用了一路反射模型;另外,国内有些学者也使用一路反射模型来对镜反射进行建模[9-10]。可见,一路反射镜反射模型应用比较广泛。同样,三路反射镜反射模型应用也较为广泛。例如,文献[11]在分析多径散射、镜反射对雷达检测性能时采用了三路反射镜反射模型;Blair等人在研究镜反射下雷达跟踪问题时采用了三路反射镜反射模型[12]。针对上述情况,雷达检测、跟踪阶段到底采用哪种镜反射模型更为准确有必要作专门的研究分析来加以说明,以便为学者们的后续研究提供参考。

本文研究分析雷达检测、跟踪阶段选择哪种镜反射模型更为准确的问题。将雷达接收目标回波信号和单脉冲比分别作为镜反射影响雷达检测、跟踪阶段的关键因素,通过建立一路反射镜反射和三路反射镜反射模型,分别推导得到了两种镜反射模型下雷达接收目标信号和单脉冲比解析表达式,仿真对比分析了采用两种镜反射模型时雷达接收目标回波信号和单脉冲比。

1 雷达接收信号

镜反射示意图如图1所示。一路反射镜反射模型考虑ABA,ABOA两路目标回波信号,三路反射镜反射模型考虑ABA,ABOA,AOBA和AOBOA四路目标回波信号。

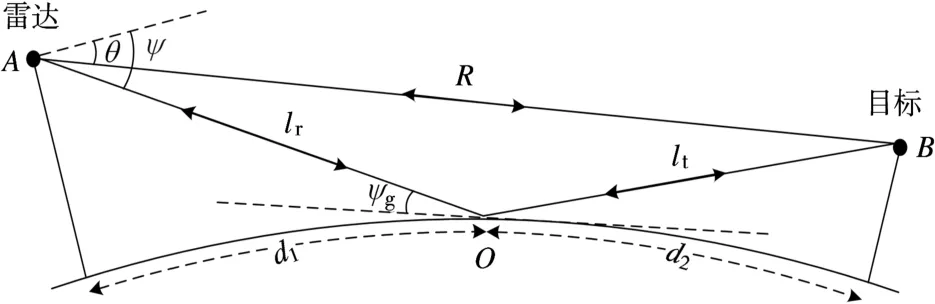
图1 镜反射示意图

对于一路反射镜反射模型,雷达接收的目标回波信号可表示为

式中,Pt为雷达发射功率,Gmax为天线最大增益,gs(θ),gs(ψ)分别为目标和反射点方向的天线电压增益,λ为发射信号波长,σ为目标RCS,Ls为收发损耗,R为雷达与目标之间的距离,ρs为镜反射系数,α为一次反射路径与直达路径的相位差。

在对雷达镜反射进行建模时,镜反射系数建模至关重要。考虑地球曲率和地面粗糙度,镜反射系数可表示为

式中,ρ0为菲涅尔反射系数:

式中,ψg为入射波掠射角,εr为反射面相对介电常数。10 GHz下的水平和垂直极化方式下地、海面菲涅尔反射系数如图2所示。

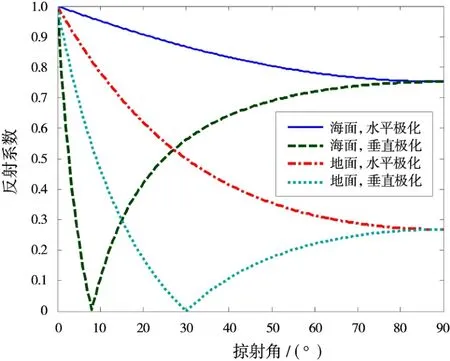
图2 菲涅尔反射系数

式(2)中,D为发散因子:

式中,Re为4/3倍的地球半径,d1,d2分别为镜反射点到雷达和目标之间的地面距离。

式(2)中,ρ1为粗糙表面反射系数的均方根值,其表示为

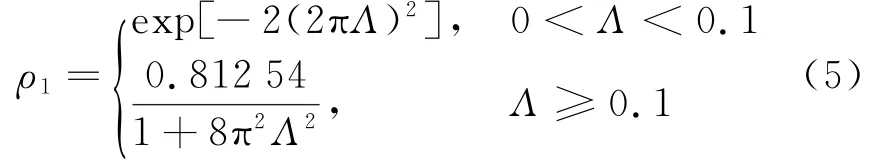
一次反射波与直达波的相位差:

式中,ϕr为反射系数的相位,

式中,lr,lt分别为反射点到雷达和目标的距离。

对于三路反射镜反射模型,雷达接收的目标回波信号可表示为

对比式(1)和式(8)可以发现,三路反射镜反射模型比一路反射镜反射模型多考虑两路目标回波信号,两种模型得到的目标回波信号是不同的。理论上,三路反射镜反射模型更能够真实反映目标镜反射回波信号形成的物理机理。但两种模型得到的目标回波信号差异到底如何,第3节将通过仿真来对比分析。

2 雷达单脉冲比

对于雷达跟踪阶段,考虑一路反射镜反射模型,则雷达和、差通道接收目标回波信号分别为

式中,

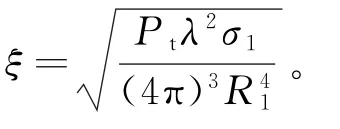
雷达单脉冲比可表示为

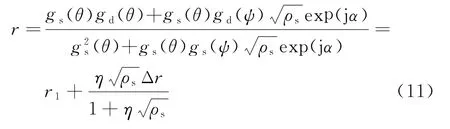
三路反射镜反射下,单脉冲比可表示为

由式(11)和式(12)可以明显看出,采用一路反射信号模型和三路反射信号模型,最终得到的单脉冲比是相同的,因此,在雷达跟踪阶段,选用一路反射和三路反射镜反射模型是等效的。

3 仿真验证

为了验证上述推导的正确性,下面通过仿真来分析不同镜反射模型下的雷达接收信号与单脉冲比。仿真参数设置如下:雷达发射功率50 k W,天线最大增益33 dB,波长0.03 m,雷达高度100 m,目标RCS为1 m2,目标以10 m的恒定高度、以300 m/s的速度朝着雷达飞行。采用一路反射和三路反射镜反射时雷达接收目标回波如图3所示。

图3表明,采用一路反射和三路反射镜反射模型得到的雷达接收目标信号的幅度和相位都不一样,且两种情况下的幅度、相位均差异较大。而对于雷达检测而言,目标回波信号幅度是决定雷达检测性能的关键因素,因此,采用两种镜反射模型时对应的雷达检测性能不同。考虑到三路反射镜反射模型更能准确反映实际镜反射产生的物理过程,针对雷达检测阶段,采用三路镜反射模型更加准确。

图3 采用一路、三路反射镜反射模型时的雷达目标回波

图4 给出了采用一路反射和三路反射镜反射模型时的雷达单脉冲比实部。从图4中可以看出,采用两种镜反射模型时的雷达单脉冲比实部相同。因此,对于雷达跟踪阶段而言,采用一路反射或三路反射镜反射模型效果一样。

4 结束语

针对雷达检测、跟踪阶段镜反射模型如何选取这一问题,本文通过对比分析一路反射、三路反射镜反射模型下雷达接收目标回波信号和单脉冲比,发现采用两种镜反射模型时的雷达接收目标回波信号差异较大、雷达单脉冲比相同。由此得出如下结论:(1)对于雷达检测阶段,选取三路镜反射模型更为精确;(2)对于雷达跟踪阶段,选用一路和三路镜反射模型时效果一样。

图4 采用一路、三路反射镜反射模型时的雷达单脉冲比实部

[1]张思远,李永祯,肖顺平.空间两点源的单脉冲测角极化响应研究[J].雷达科学与技术,2015,13(5):467-472.

ZHANG Siyuan,LI Yongzhen,XIAO Shunping.Polarimetric Response for Dual-Point Sources in Monopulse Angular Measurement System[J].Radar Science and Technology,2015,13(5):467-472.(in Chinese)

[2]徐振海,熊子源,宋聃,等.阵列雷达双零点单脉冲低角跟踪算法[J].国防科技大学学报,2015,37(1):130-135.

[3]吴向东,马仑,梁中华.基于波束域的米波雷达低仰角波达方向估计[J].电波科学学报,2014,29(6):1147-1152.

[4]徐振海,熊子源,肖顺平.基于频率分集的阵列雷达低角跟踪算法[J].国防科技大学学报,2014,36(2):93-98.

[5]祝明波,车驰峰,邹建武,等.超低空反导中的多径效应及其抑制研究综述[J].飞航导弹,2015(11):64-67.

[6]BARTON D K.Low-Angle Radar Tracking[J].Proceedings of the IEEE,1974,62(6):687-704.

[7]DAEIPOUR E,BLAIR W D,BAR-SHALOM Y.Bias Compensation and Tracking with Monopulse Radars in the Presence of Multipath[J].IEEE Trans on Aerospace and Electronic Systems,1997,33(3):863-882.

[8]WILSON S L,CARLSON B D.Radar Detection in Multipath[J].IEE Proceedings-Radar,Sonar and Navigation,1999,146(1):45-54.

[9]董玫,赵永波,张守宏.米波段下海面多径模型研究[J].电子学报,2009,36(6):1373-1377.

DONG Mei,ZHAO Yongbo,ZHANG Shouhong.The Analysis of the Multipath Model Under the VHF Band at Sea[J].Acta Electronica Sinica,2009,36(6):1373-1377.(in Chinese)

[10]杨勇,王雪松,张文明,等.多径环境下海面低空目标检测技术研究[J].电波科学学报,2011,26(3):443-449.

YANG Yong,WANG Xuesong,ZHANG Wenming,et al.Detection Technology of Low-Flying Target on the Sea in Multipath Environment[J].Chinese Journal of Radio Science,2011,26(3):443-449.(in Chinese)

[11]YANG Yong,FENG Dejun,WANG Xuesong,et al.Effects of K Distributed Sea Clutter and Multipath on Radar Detection of Low Altitude Sea Surface Targets[J].IET Radar,Sonar and Navigation,2014,8(7):757-766.

[12]BLAIR W D,BRANDT-PEARCE M.Statistics of Monopulse Measurements of Rayleigh Targets in the Presence of Specular and Diffuse Multipath[C]∥2001 IEEE Radar Conference,Atlanta,GA:IEEE,2001:369-375.