众筹筑屋规划方案设计的优化数学模型及其应用

隋欣

摘 要 本文首先介绍了常见的优化数学模型，其次对2015年全国大学生数学建模竞赛专科组D题众筹筑屋规划方案设计问题进行分析，建立优化模型，并利用Mathematica 软件编程得到最优解。

关键词 众筹筑屋规划 优化模型 Mathematica软件

中图分类号：O224 文献标识码：A DOI：10.16400/j.cnki.kjdks.2015.12.024

Optimization Mathematical Model of Building a House to

Raise Public Planning and its Application

SUI Xin

（Public Education Department， Changchun Automobile Industry Institute， Changchun， Jilin 130000）

Abstract This paper introduces the common optimization mathematical model， and secondly for 2015 National Mathematical Contest in Modeling Specialist Group D title Public building a house plan designed to raise the problem analysis， the optimal model， and using Mathematica software programming to get the optimal solution.

Key words building a house to raise public planning； optimization model； Mathematica software

在工程技术、经济管理、科学研究和日常生活等诸多领域中，人们经常遇到的一类决策问题：在一系列客观或主观限制条件下，寻求所关注的某个或多个指标达到最大（或最小）的决策。数学上称为最优化问题，研究处理这种问题的方法叫最优化方法，建立的模型叫优化模型。优化模型一般有下面三个要素：决策变量、目标函数、约束条件。常见的优化模型有：线性规划模型、整数线性规划模型、非线性规划模型等。

（1）线性规划模型（目标函数和约束条件关于决策变量都是线性的）：（） =

（2）整数线性规划模型（某些决策变量或全部决策变量必须取整数）：（） =

（3）非线性规划模型（目标函数和约束条件包含有非线性函数）：

下面针对2015年全国大学生数学建模竞赛专科组D题众筹筑屋规划方案设计问题利用优化模型求解。（原题和附件省略）

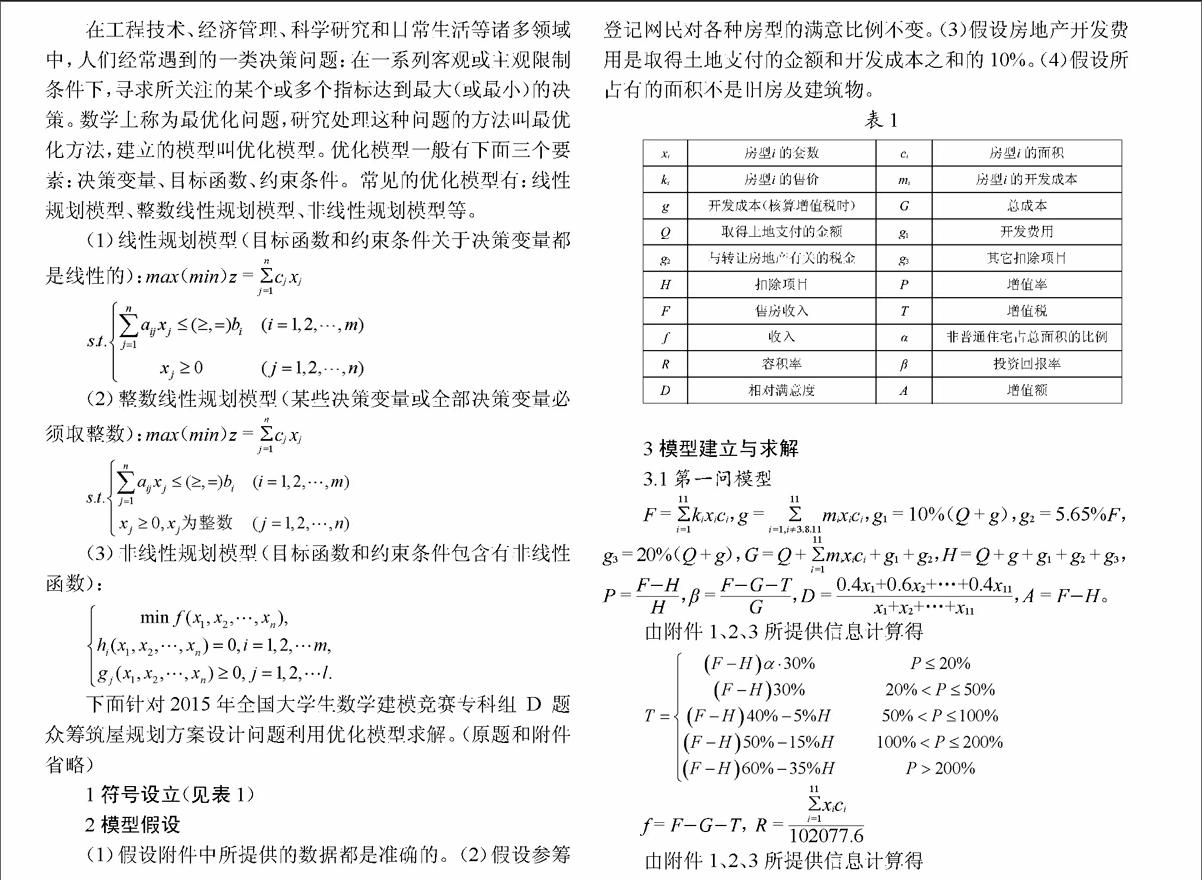
1 符号设立（见表1）

2 模型假设

（1）假设附件中所提供的数据都是准确的。（2）假设参筹登记网民对各种房型的满意比例不变。（3）假设房地产开发费用是取得土地支付的金额和开发成本之和的10%。（4）假设所占有的面积不是旧房及建筑物。

表1

3模型建立与求解

3.1 第一问模型

= ， = ， = 10%（ + ）， = 5.65%， = 20%（ + ）， = + + + ， = + + + + ， = ， = ， = ， = 。

由附件1、2、3所提供信息计算得

= ， =

由附件1、2、3所提供信息计算得

= 2484163080， = 641684687.9，

= 120872232.4， = 2.275209825，

= 539418294.9， = 0.199245726，

= 0.25831021， = 0.583

3.2 第二问模型

为了满足参筹者的购满意愿，建模非线性整数规划模型：

=

Mathematica程序如下：

Maximize[{（0.4x1+0.6x2+0.5x3+0.6x4+0.7x5+0.8x6+0.9x7 +0.6x8+0.2x9+0.3x10+0.4x11）/（x1+x2+x3+x4+x5+x6+x7+x8+x9 +x10+x11），（77x1+98x2+117x3+145x4+156x5+167x6+178x7+126x8） 102077.6*2.28，50<=x1<=450，50<=x2 500，50<=x3 300，150<=x4<=500，100<=x5 550，150<=x6 350，50<=x7<=450，100<=x8 250，50<=x9？350，50<=x10<=400，50<=x11？250，x1+x2+x3+x4+x5+x6+x7+x8+x9+x10+x11 1950，Element[{x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11}，Integers]}，{x1，x2，x3，x4，x5，x6，x7，x8，x9，x10，x11}]

运行结果：

{0.649008，{x1 50，x2 167，x3 50，x4 150，x5 227，x6 316，x7 450，x8 123，x9 50，x10 132，x11 250}}

对方案Ⅱ进行核算得，

= 2274632870， = 460166154.2，

= 79980976.09， = 1.989662766，

= 286548974.9， = 0.113339711，endprint

= 0.202303484， = 0.706897

3.3 第二问模型

根据问题二中计算结果投资回报率未达到25%，故优化模型把达到25%作为约束条件解出相应数据，代入程序当中求出方案。

建立非线性规划模型：

=

利用Mathematica软件对数据进优化处理时发现，当≥50%时没有可行解，而当≤20%时容积率、投资回报率等未达到要求，故将增值率限定在20%≤≤50%内。

Mathematica程序如下：

k={12000，10800，11200，12800，12800，13600，14000，10400， 6400，6800，7200}；xx=Array[x，11]；mm={77，98，117，145，156， 167，178，126，103，129，133}；f=Sum[mm[[i]]*k[[i]]*x[i]，{i，1，11}]；g0=77*4263*x[1]+98*4323*x[2]+145*5288*x[4]+156*5268*x[5]+167*5533*x[6]+178*5685*x[7]+103*2663*x[9]+129*2791 *x[10]；g00=g0+117*4532*x[3]+126*4323*x[8]+133*2982*x[11]；q=777179627；g1=0.1（q+g0）；g11=0.1（q+g00）；g22=g2=f*0.0565；g3=0.2（q+g0）；g33=0.2（q+g00）；g=q+g0+4532*x[3]+4323*x[8]+2982*x[11]+g11+g22；h=q+g0+g1+g2+g3；b1=77x[1]+98x[2]+117x[3]；b2=145x[4]+156x[5]+167x[6]+178x[7]+126x[8]+133x[11]；k1=b1/（b1+b2）；k2=b2/（b1+b2）；a12=103x[9]k2；a22=129x[10]k2；a11=103x[9]k1；a21=129x[10]k1；m=（a12+a22+b2）/（b1+b2+102x[9]+129x[10]）；Maximize[{（0.4x[1]+0.6x[2]+0.5x[3]+0.6x[4]+0.7x[5]+0.8x[6]+0.9x[7]+0.6x[8]+0.2x[9]+0.3x[10]+0.4x[11]）/（x[1]+x[2]+x[3]+x[4]+x[5]+x[6]+x[7]+x[8]+x[9]+x[10]+x[11]），50 x[1] 450，50 x[2] 500，50 x[3] 300，150 x[4] 500，100 x[5] 550，150 x[6] 350，50 x[7] 450，100 x[8] 250，50 x[9] 350，50 x[10] 400，50 x[11] 250，77x[1]+98x[2]+117x[3]+145x[4]+156x[5]+167x[6]+178x[7]+126x[8] 102077.6*2.28，1.2h

运行结果：{0.6939577039274925， {[1]→50， [2]→50， [3]→71， [4]→150， [5]→136， [6]→347， [7]→450， [8]→250， [9]→51， [10]→50， [11]→50}}

将数据带入模型计算得： = 2.24899， = 0.693958， = 0.321106达到要求，项目能被执行。

参考文献

[1] 韩中庚.数学建模方法及其应用[M].北京：高等教育出版社，2009.