船舶轴系纵向振动共振转换器的设计与优化
王珺++蒋炎坤++王钊轶++马磊


摘要: 针对某船舶轴系进行模态和谐响应分析,对该轴系进行共振转换器(Resonance Changer,RC)的结构设计.基于动力调频减振理论和一维搜索法,对该RC进行优化设计,获得最佳参数.通过对比未加RC和加装已优化RC前后轴系的固有频率和关键位置处最大振幅,发现加装RC后,轴系1阶固有频率提高2倍以上,关键位置处的最大振幅降低约90%,调频减振效果明显.
关键词: 船舶轴系; 共振转换器; 模态分析; 谐响应; 优化设计
中图分类号: U664.21文献标志码: B
0引言
船舶轴系的纵向振动主要由纵向激振力造成.随着船舶大型化和主机功率的增大,虽然主机的强度也会增大,但临界转速仍可能落入工作转速范围内而引起共振,故轴系纵向振动的研究愈发受到关注,最有效的方法之一是安装纵向减振器.目前船舶轴系上的纵向减振器多是通过活塞在阻尼油箱内来回挤压阻尼油以达到减振效果,这种减振器不能调节轴系固有频率;而共振转换器(Resonance Changer, RC)不仅可以达到减振效果,也可以实现调频目的,且对于不同的轴系均可调节轴系振动频率.
20世纪60年代,英国Michell轴承公司将安装在推力轴承上的推力仪改成轴系共振调整器,通过油缸及其连接管路,减小推力环刚度,降低轴系纵向振动固有频率,从而减小传递到船体的激振力.21世纪初,国外学者研究潜艇轴系安装RC以降低传递到壳体与振动相关的刚度函数.[14]国内学者刘耀宗等[5]用功率流评价并分析动力吸振器不同安装位置和数目的减振效果,李良伟等[6]对动力吸振器进行参数优化以减小推进轴系的纵向振动,但没对RC的结构设计和优化的研究.
本文以某轴系为研究对象,分析其纵向振动特性,根据该轴系的结构和动力调频减振器的原理设计RC,基于有限元法对加装该减振器的轴系进行分析;再利用动力调频减振理论和一维搜索法,对该RC进行优化设计,并对加装后的轴系进行效果检验与分析.
1RC的设计
1.1轴系纵向振动的模态分析和受迫振动分析
假设某轴系结构示意见图1,轴系基本参数见表1.轴系由尾轴、推力中间轴、推力轴等组成,总长为15.500 m.其中尾轴长10.000 m,前半段外径0.290 m,内径0.165 m;后半段外径0.280 m,内径0.165 m.推力轴与推力中间轴的直径均为0.280 m,长度为2.000和1.000 m.纵向减振器轴直径为0.280 m,长度为2.000 m,弹性联轴器长0.500 m.
图 1轴系结构示意, mm
Fig.1Schematic of shafting structure, mm
表 1轴系基本参数
Tab.1Basic parameters of shafting钢密度/
(kg/m3)钢弹性模
量/(N/m2)材料
泊松比推力轴承
刚度/(N/m)螺旋桨平均
推力/N7.8×1032.0×10110.39.8×1071.45×106
简化处理后建立轴系有限元计算模型,对轴系施加载荷,设定约束条件,最后利用求解器求解并计算(具体计算方法见文献[7]).提取轴系纵向振动的5阶模态,见表2.在船舶行驶时,中高频段范围内螺旋桨非定常激励力不能对船体形成有效激励,故在研究主推进轴系纵向振动时,一般将激励频率限制在 100 Hz以下[8];行驶时轴系转速不高,在0~1 000 r/min范围内.由此可知:1阶固有频率对船舶行驶有较大影响,避免在1阶固有频率附近发生共振需提高该阶次的固有频率并降低振动振幅.
表 2轴系模态分析结果
Tab.2Results of modal analysis on shafting阶
次固有
频率/Hz临界转速/
(r/min)最大相对位移/
(103m)17.434 3446.0584.7532107.566 453.6007.9413268.7116 122.6009.0044375.8022 548.0008.2815548.5032 910.00010.14
对轴系进行受迫振动计算[7]分析,表明该轴系螺旋桨、推力轴承和弹性联轴器的振幅随振动频率变化趋势一致,频率小于10 Hz的范围内振幅变化很大,即该范围内可能发生共振,轴系关键位置在0~100 Hz范围内对应的最大振幅值见表3.
表 3轴系关键位置处激振振幅
Tab.3Vibration amplitude of key position轴系位置最大幅值时频率/Hz最大幅值/(103m)螺旋桨87.584推力轴承87.541弹性联轴器87.551
1.2RC机理
RC实质上是一种液压动力吸振器[9],其将一个弹性质量阻尼装置安放到原物理系统中,以降低轴系对纵向脉动力的响应,通过控制活塞缸内的液压介质,使液压介质在活塞缸与液压缸之间流动.纵向激振力克服液压介质的惯性力、阻尼力及阻力做功,产生的热量被冷却器带走,将振动的能量吸收,达到减振效果.RC结构简图见图2.
图 2RC结构简图
Fig.2Simplified diagram of RC structure
图2中:P0为减振器的前后压力;A1为连接管截面积;V1为油箱体积;元件1为活塞;元件2为缸体;元件3为连接管;元件4为油箱.
假定油箱为刚性,油箱中充满被压缩的油,则推力活塞缸内作用在管道上的压力应等于克服管道内油的惯性的力、克服管道内黏性的阻力和克服压缩油箱内的油所需力的和.endprint
假设流动是层流,液压管长度和圆管管长相等,可得管路平衡方程为
P1=ρ1A1L1(x¨1-x¨b)A0A1+
8πμ1L1(x·1-x·b)A0A1+A1B1(x1-xb)A0V1(1)
式中:A0为活塞缸截面积;B1为油的体积模量.选择船用68号滑油作为RC液压阻尼油,其具有良好的抗腐蚀性、抗乳化性、抗磨性、抗剪切性、清净性以及对密封材料影响小的优点.
假设理想质量m1=ρ1A20L1/A1,理想阻尼c1=8πμ1L1A20/A21,理想刚度k1=A20B1/L1,简化上式得P0=m1(x¨1-x¨b)+c1(x·1-x·b)+k1(x1-xb)(2)1.3RC结构设计
RC在轴系中的安装位置见图3.RC可分为前减振器,后减振器和推力环3个部分.2个减振器中间夹着推力环,推力环随轴系振动和旋转,2个纵向动力减振器确保轴系的前后振动都受到缓冲.
图 3RC安装图
Fig.3Installation diagram of RC
RC安装在推力轴承的任何位置都可以达到减振的目的.考虑到推力轴承可承受部分激振能量,故RC放置在推力轴承前面效果更佳.
推力环与推力滚子轴承间会产生摩擦,需进行润滑,故RC结构中设专门润滑油管道,利用油泵循环使用润滑油.
RC设计需考虑的因素还有:纵向减振器上可承受的推力振动、油箱尺寸、连接管道长度以及管道的孔径.
设计的RC结构见图4,其主要组成部分有壳体、换热器和油箱.壳体中设有环形活塞组件和活塞缸.环形活塞组件由推力块和环形活塞组成,环形活塞上套有密封圈.环形活塞组件在环形活塞缸中往复运动,环形活塞缸的底部两端有与油箱联通的孔.换热器中设有连接活塞缸和油箱的连接管路,管路周围流动冷却油,用于带走压缩油箱时产生的热量.换热器由外壳和内壳组成,分别连接油箱和液压缸.油箱是一个环形液压缸,设有排除空气的排气阀,上部两端设置进油管.液压缸承受较大的压力,其密封性需得到保证.
图 4设计的RC结构
Fig.4RC structure obtained by design
根据设计的RC平面图,使用Pro/E进行三维建模,通过三维模型能更清晰地看到其内部结构,见图5.
a)RC分解视图
b)RC外观图
图 5RC三维模型
Fig.53D model of RC
1.4RC系统设计
根据不同的应用场合,可以将多个RC以串联或并联的方式连接在一起,这样的组合方式可以使调整的纵向振动频率范围更广,效果更明显.
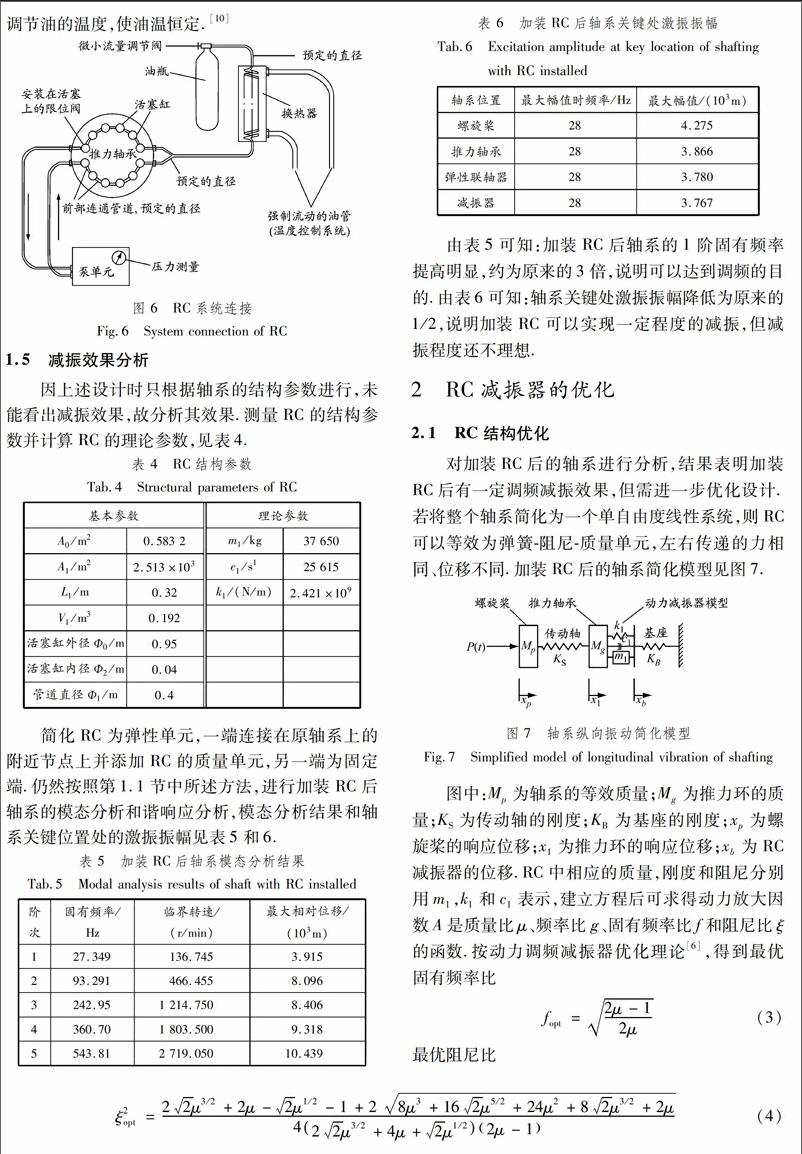
所设计的RC系统用于液压系统时的连接见图6.该RC系统采用串并联混合.在活塞与壳体之间的活塞缸内充满油,各相邻油缸之间通过管道相连.在一个活塞上安装“限制阀”,这个活塞缸与泵单元的回油接口相连,另外一端的油缸与泵油单元的输油接口相连.其中泵单元可以测量活塞缸中的油压,保证活塞缸中一直都充满油.另有2个活塞缸与油瓶相连,安装微小流量调节阀可以调节活塞中的油压,保证推力活塞缸中的压力稳定,油量充足.此外,在推力活塞缸与油瓶之间的连接管道上配置冷却器调节油的温度,使油温恒定.[10]
图 6RC系统连接
Fig.6System connection of RC
1.5减振效果分析
因上述设计时只根据轴系的结构参数进行,未能看出减振效果,故分析其效果.测量RC的结构参数并计算RC的理论参数,见表4.
表 4RC结构参数
Tab.4Structural parameters of RC基本参数A0/m20.583 2A1/m22.513×103L1/m0.32V1/m30.192活塞缸外径Ф0/m0.95活塞缸内径Ф2/m0.04管道直径Ф1/m0.4理论参数m1/kg37 650c1/s125 615k1/(N/m)2.421×109
简化RC为弹性单元,一端连接在原轴系上的附近节点上并添加RC的质量单元,另一端为固定端.仍然按照第1.1节中所述方法,进行加装RC后轴系的模态分析和谐响应分析,模态分析结果和轴系关键位置处的激振振幅见表5和6.
表 5加装RC后轴系模态分析结果
Tab.5Modal analysis results of shaft with RC installed阶
次固有频率/
Hz临界转速/
(r/min)最大相对位移/
(103m)127.349 136.745 3.915293.291 466.455 8.0963242.95 1 214.750 8.4064360.70 1 803.500 9.3185543.812 719.05010.439表 6加装RC后轴系关键处激振振幅
Tab.6Excitation amplitude at key location of shafting
with RC installed轴系位置最大幅值时频率/Hz最大幅值/(103m)螺旋桨284.275推力轴承283.866弹性联轴器283.780减振器283.767
由表5可知:加装RC后轴系的1阶固有频率提高明显,约为原来的3倍,说明可以达到调频的目的.由表6可知:轴系关键处激振振幅降低为原来的1/2,说明加装RC可以实现一定程度的减振,但减振程度还不理想.
2RC减振器的优化
2.1RC结构优化
对加装RC后的轴系进行分析,结果表明加装RC后有一定调频减振效果,但需进一步优化设计.若将整个轴系简化为一个单自由度线性系统,则RC可以等效为弹簧阻尼质量单元,左右传递的力相同、位移不同.加装RC后的轴系简化模型见图7.endprint
图 7轴系纵向振动简化模型
Fig.7Simplified model of longitudinal vibration of shafting
图中:Mp为轴系的等效质量;Mg为推力环的质量;KS为传动轴的刚度;KB为基座的刚度;xp为螺旋桨的响应位移;x1为推力环的响应位移;xb为RC减振器的位移.RC中相应的质量,刚度和阻尼分别用m1,k1和c1表示,建立方程后可求得动力放大因数A是质量比μ、频率比g、固有频率比f和阻尼比ξ的函数.按动力调频减振器优化理论[6],得到最优固有频率比fopt=2μ-12μ(3)最优阻尼比ξ2opt=22μ3/2+2μ-2μ1/2-1+28μ3+162μ5/2+24μ2+82μ3/2+2μ422μ3/2+4μ+2μ1/22μ-1(4)由于fopt和ξopt在μ>0.5时为实数;在μ≤0.5时为非实数,故在μ≤0.5时采取其他方法.
在μ≤0.5时,选择一维搜索法解决RC减振器参数优化问题,这是一种最大值的最小化方法[1113].基本步骤如下:首先设定质量比μ为定值,然后确定施加的激振力的频率范围,并按一定精度把f和ξ这2个参数所选择的分析区间离散,这时就得到N组(fi,ξi)(i=1,2,3,…,N)值,再把每组(fi,ξi)值代入A(g,f,μ,ξ)方程中,就可以得到频率比g与动力放大因数A的关系曲线.
研究不同的优化目标函数[11,14],并对比其结果,可知取面积和峰值平方和为目标函数时最为接近理论曲线,因此采用的目标函数为最小化动力放大系数曲线与横坐标的面积和峰值平方和.记每组(fi,ξi)对应的动力放大因数曲线A(g,fi,μi,ξi)与横坐标所围成的面积为Si,并记曲线峰值为Mij,(j=1,2,3,…,Zi,Zi为该曲线峰值点个数),则目标函数可用公式表示为minfi,ξi1≤i≤N P=Si+Zij=1M2ij(5)目标函数所对应的fopt值和ξopt值就是最优固有频率比和最优阻尼比,实现动力减振参数优化.该优化方法采用MATLAB编程计算,结果见图8.
图 8质量比最优固有频率/最优阻尼比曲线
Fig.8Curves of mass ratio against optimal natural
frequency and optimal damping ratio
由图8可知:随着质量比的增加,最优固有频率不断增加,最优阻尼比不断下降,说明质量比与最优固有频率成正比,与最优阻尼比成反比.从图中可以选取最优固有频率和最优阻尼比.
选取无量纲参数,代入理想质量、阻尼和刚度计算式,得优化后的RC结构尺寸,见表7.
2.2优化效果分析
对加装优化RC的轴系进行模态分析,结果见表8.与表2进行对比可知:加装优化RC后的轴系固有频率得到提高,尤其在1阶固有频率时,固有频率是原来的2倍多,并使最大相对位移值减小.
表 7优化后RC结构尺寸
Tab.7Structure size of optimized RC基本参数A0/m20.352A1/m21.402×103L1/m0.491V1/m30.210Ф0/m0.780Ф2/m0.040Ф1/m0.042理论参数m1/kg37 650c1/s17 716 535k1/(Ω/m)9.0×108f0.89μ2.51ξ0.398 5
表 8加装优化RC的轴系模态分析结果
Tab.8Modal analysis results of shafting with optimized
shafting installed阶次固有频率/
Hz临界转速/
(r/min)最大相对
位移/(103m)1 17.411 044.6 3.6462 92.345 540.4 8.2173242.7914 567.4 8.4104360.6721 640.2 9.3225543.7932 627.410.461
对加装优化RC的轴系进行谐响应分析,轴系关键部位的最大幅值见表9,并与未加装RC及加装未优化RC的最大振幅对比,见表10.
表 9加装优化RC的轴系关键处的激振振幅
Tab.9Excitation amplitude at key position of shafting
with RC installed轴系位置最大幅值时频率/Hz最大幅值/(103m)螺旋桨180.340推力轴承180.321弹性联轴器180.318减振器180.317
表 10最大振幅对比
Tab.10Comparison of maximum amplitudemm轴系位置未加RC加未优化RC加优化RC螺旋桨7.5844.2750.340推力轴承7.5413.8860.321弹性联轴器7.5513.7803.767减振器7.5843.7670.317
表9和10表明:加装优化RC的轴系在激振频率为18 Hz(约等于1阶固有频率)时,轴系上节点的振动位移最大时,各个轴系关键位置的幅值最大;螺旋桨处振动位移最大,弹性联轴器、RC处位移最小.由表10还可知:加装优化RC后的轴系降低原未装RC轴系振动幅值约90%,减振效果十分明显,并满足规范要求.
3结论
以某船舶轴系为研究对象,设计一种轴系纵向RC,并对其参数进行优化,结果表明:
1)根据轴系结构设计的RC可以实现调频,但减振作用不明显,需对RC的结构进行优化.
2)基于动力调频减振理论和一维搜索法,获得RC的最优固有频率比和最优阻尼率,并以此优化RC参数.对比是否加装优化RC的轴系固有频率和关键处的最大振幅,表明加装优化的RC后可以使轴系的1阶固有频率提高2倍以上,关键处的最大振幅降低约90%,调频减振效果明显,可以满足规范标准.参考文献:endprint
[1]MERZ S, KINNS R, KESSISSOGLOU N. Effect of a submarine shaft resonance changer in the presence of fluid forces[C]//Proc 7th European Conf Struct Dynamics. Southampton, 2008.
[2]MERZ S, KESSISSOGLOU N J, Kinns R. Excitation of a submarine hull by propeller forces[C]//Proc 14th Int Congress Sound & Vibration. Cairns, 2007.
[3]KINNS R, THOMPSON I, KESSISSOGLOU N, et al. Hull vibratory forces transmitted via the fluid and the shaft from a submarine propeller[J]. Ships & Offshore Structures, 2007, 2(2): 183189.
[4]CARESTA M, KESSISSOGLOU N, TSO Y. Low frequency structural and acoustic responses of a submarine hull[J]. Acoustics Australia, 2008, 36(2): 4752.
[5]刘耀宗, 王宁, 孟浩, 等. 基于动力吸振器的潜艇推进轴系轴向减振研究[J]. 振动与冲击, 2009, 28(5): 184187.
LIU Yaozong, WANG Ning, MENG Hao, et al. Design of dynamic vibration absorbers to reduce axial vibration of propelling shafts of submarines[J]. J Vibration & Shock, 2009, 28(5): 184187.
[6]李良伟, 赵耀, 陆坡, 等. 减小船舶轴系纵向振动的动力减振器参数优化[J]. 中国造船, 2010, 51(2): 139146.
LI Liangwei, ZHAO Yao, LU Po, et al. Optimization of dynamic absorber parameters for reducing axial vibration of ship shafting[J]. Shipbuilding China, 2010, 51(2): 139146.
[7]马磊. 船舶轴系纵向减振器性能研究[D]. 武汉: 华中科技大学. 2011(5): 1317, 1921.
[8]张赣波. 船舶主推进轴系纵向振动主动控制方法研究[D]. 武汉: 华中科技大学. 2012(1): 51.
[9]曹贻鹏. 推进轴系引起的艇体结构振动与辐射噪声控制研究[D]. 哈尔滨: 哈尔滨工程大学. 2008(6): 68.
[10]蒋炎坤, 马磊, 吴崇健, 等. 纵向减振调频器系统: 中国, 201120212841[P]. 20120229.
[11]侯祥林, 李和玉, 刘杰. 最大值最小化问题的优化算法与多自由度动力减振器参数计算[J]. 振动与冲击, 2008, 27(1): 100103.
HOU Xianglin, LI Heyu, LIU Jie. Optimal algorithm for minimization of maximum value problems and application of dynamic absorbor with multiDOF[J]. J Vibration & Shock, 2008, 27(1): 100103.
[12]王伟, 赵庆海, 张海燕. 动力减振器参数优化分析[J]. 振动与冲击, 2006, 25(5): 180182.
WANG Wei, ZHAO Qinghai, ZHANG Haiyan. Analysis of optimal parameters of dynamic reducer[J]. J Vibration & Shock, 2006, 25(5): 180182.
[13]张洪田, 刘志刚, 王芝秋, 等. 多自由度振动系统动力吸振器参数优化设计方法及分析[J]. 哈尔滨工程大学学报, 1996, 17(2): 1924.
ZHANG Hongtian, LIU Zhigang, WANG Zhiqiu, et al. Optimum design method of dynamic absorber for multidegreeoffreedom vibration systems[J]. J Harbin Eng Univ, 1996, 17(2): 1924.
[14]师汉民. 机械振动系统[M]. 2版. 武汉: 华中科技大学出版社, 2004.(编辑武晓英)第24卷 第6期2015年12月计 算 机 辅 助 工 程Computer Aided EngineeringVol.24 No.6Dec. 2015endprint

