只有充类至尽 才能触类旁通*——谈物理教学中如何做到触类旁通

只有充类至尽 才能触类旁通*
——谈物理教学中如何做到触类旁通

罗贤辉

(南京市第十二中学江苏 南京210011)

*江苏省中小学教学研究2013年度第十期课题“基于新课程标准的高中物理深度备课行动研究”，项目编号：2013JK10-L002

摘 要：举例说明教学中对新知识的外延部分作充分的推究，是深化知识的一种途径，促使学生遇到问题时能够做到触类旁通.只有对知识 “充类至尽”才能做到“触类旁通”.

关键词：知识外延推论触类旁通

收稿日期：(2014-12-01)

“充类至尽”，语出《孟子》，即推究同类事理到极精密处，指就事理作充分的推论.“触类旁通”，语出《周易》，指掌握了某一事物的规律，就能推知同类事物.

教学活动中，教师通常会对相似的问题做归纳，找出共性归为一类，形成专题，期望学生以后面对这类问题时，能做到“触类旁通”，举一反三.这显然是一种很高效的教学方法.笔者认为，对问题归类时，既要看到共性，更要看到差异和细节，见微知著方能弄清本质.这要求教师在教学中须对知识点外延部分作细致推究，做到“充类至尽”，使学生理解问题的方方面面，才能让学生在面对同类问题时做到“触类旁通”.

下面举一个静力学的例题说明这个道理，难度从“高考要求”过渡到“竞赛水平”，效果从“笔算”过渡到“口算”.目的不是为了解题，而是强调细致推究可以起到事半功倍的效果，遇到类似问题时也不必从头再来.推究过程做到“充类至尽”，使缺乏数学基础的高一学生接受起来也能轻松愉快，毫不费力.

【例题】静止于水平面上质量为m的物体，受到一个与竖直方向成θ角的力F的作用，无论F为多大，都不能推动该物体，求物体与地面间的动摩擦因数至少为多大(最大静摩擦力按滑动摩擦力计算).

这是一道普通的静力学问题，高一学生既没有三角变换知识，又缺乏处理复合函数的能力，需要教师做大量的点拨.即使学过三角函数后，学生可以借助数学工具解出正确结果，却又难以理解其力学本质，只能就题论题，无法做到触类旁通推及其他.先看常规解法的局限性.

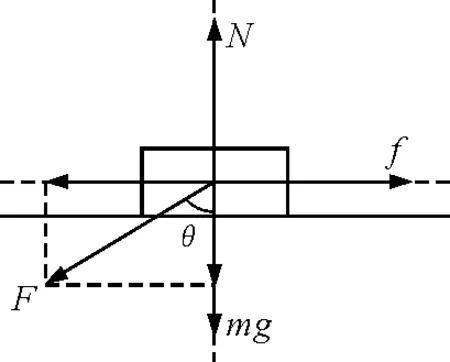
图1

正交分解法：物体受力如图1，因其处于静止状态，故水平方向

Fsinθ=f

竖直方向

N=mg+Fcosθ

又

f=μN

所以

F(sinθ-μcosθ)=μmg

因与F无关，所以

sinθ-μcosθ=0

即

μ=tanθ

正交分解法公正平和，四平八稳，是中学物理中重要的解题方法，其对学生的教育意义是多力平衡时要养成进行正交分解的习惯.不足之处是过于机械，不利于发散思维的培养.

推究1:分析力的作用效果.既是力学平衡问题，自然要从力的作用效果出发.与外力F的大小无关，说明在外力增大了ΔF的过程中，因外力变大而增加的动力效果与增加的阻力效果抵消，即

ΔFsinθ=μΔFcosθ

所以

μ=tanθ

推究1着眼于施加外力后，对物体产生的影响互相抵消这一力学本质，理解容易，计算简单，不需要三角函数作前提，比正交分解法简洁高效得多.这一物体静止现象称为“力学自锁现象”，理解其原理，学生便可以轻松地解释“螺栓与螺母”间的关系、螺旋式千斤顶等机械的工作机理.

触类旁通1:如图2，质量为m的物体静止于倾角为θ的斜面上，现用一竖直向下的力F压物体，能否使物体沿斜面下滑？

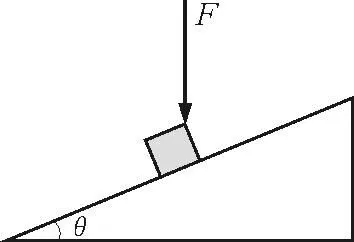
图2

物体能静止在斜面上，说明

mgsinθ=μmgcosθ

而外力F的方向竖直向下，与重力方向相同，故

Fsinθ=μFcosθ

增加的动力效果与阻力效果互相抵消，所以无法推动物体下滑.学生只需看一眼便可得出结论.若用正交分解法，岂不要从头再来？当然，此题也可以把压力等效为增大了物体的重量来理解，思路也很简单.

推究2:分析力的作用特征.例题中提示最大静摩擦力可当成滑动摩擦力来计算，而滑动摩擦力与正压力成正比，即摩擦力与支持力的合力T的方向保持不变，如图3所示.从图中看出，如果推力F沿着T的反方向推动，则无论F多大，其增加的动力效果ΔFsinθ总与其增大的阻力效果μΔFcosθ相抵消，若θ<α，则Fsinθ<μFcosθ总成立，无论多大的力都无法推动物体，故临界位置处

即

μ=tanθ

图3

推究2着眼于一个细节，即“滑动摩擦力与正压力成正比”，由此可以推出“摩擦力与支持力的合力方向保持不变”这一结论，可谓小中见大出奇制胜！合力与竖直方向不变的夹角称为“摩擦角”，这一概念原属于竞赛内容，近些年高考中却屡有提及，从发展学生思维角度出发并不过分，毕竟不是十分繁难的内容，只要合理安排，学生接受起来并无障碍.

触类旁通2:用力拉着一个物体沿水平面匀速前进，已知水平面与物体间的动摩擦因数为μ，问拉力沿什么方向时最省力？

高一学生没有学过利用三角函数求极值的数学方法，掌握摩擦力特征的上述推论后，可以成功避开数学障碍.先把摩擦力与支持力合成一个力T，且T的方向不变.然后应用熟悉的“图解法”求得正确结果，如图4所示.当拉力的方向与T垂直，即拉力与水平面的夹角

时即拉力最小.

图4

不难看出，这一能力要求较高的静力学问题，经过分析，最终可以“口算”出结果来，否则就需要借助于艰涩的数学推导来求函数的极值了.

可见，方法简单源于对摩擦力“周边知识”的精细推究，本题分析出平衡问题的“类型”后没有停留在常规的解法上，而是继续分析得出推不动的本质原因，这是对知识点的进一步“深化”，接着再分析得出推力变化但合力的方向不变这一特征，这已经是对原知识点的“升华”了，使之由一道普通例题，演变成与之相关的更深入的其他问题.若在讲授每个知识点时，教师都像这样力求穷尽其理“充类至尽”，展示出知识的丰富外延，那么学生就能细究缘由“触类旁通”，养成良好的思维习惯.遇到类似问题时，学生也就能做到举一反三，闻一知十.