一个力学问题的数学解法

一个力学问题的数学解法

钱厚旺陈玉奇

(江苏省姜堰中等专业学校江苏 泰州225500)

【题目】(2014年全国周培源大学生力学竞赛第3题)：有一个内壁光滑的固定容器，如图1所示，该容器的内壁是一条抛物线绕着其对称轴旋转而得到的曲面．为了确定这条抛物线的方程，小明和小刚用一根长度为400 mm的同样光滑的匀质直杆AB数次随意放入容器之中时，发现尽管各次放入后杆件滑动和滚动的情况都不一样，但最终静止时与水平面的夹角每次都是45°，试确定这条抛物线的方程．

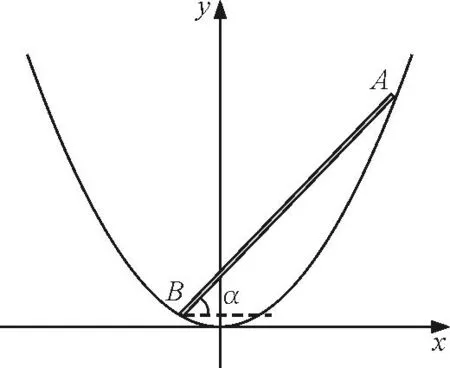
图1

本题可用大学物理中的最小势能原理、虚位移原理或刚体静力学的知识分析求解，详见解答和评分标准．但对于该题，也可以从数学的角度，用高中知识来求抛物线的方程．

解析：作出杆AB的受力情况，如图2．根据3力汇交原理可知，杆平衡时，弹力N1，N2和重力G必相交于一点，记为D．

图2

设杆AB静止时与水平方向的夹角为α，其直线方程为y=kx+b，k=tanα．并设抛物线方程为y=ax2，杆与抛物线的交点坐标为A(x1,y1)、B(x2,y2)，质心坐标为C(m,n)，则有

x1+x2=2m

将质心坐标C(m,n)代入y=kx+b,求出

b=n-km

所以

y=kx+n-km

则直线和抛物线的交点满足方程

ax2-kx-n+km=0

由韦达定理并结合质心坐标，有

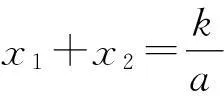
所以

2am=k

设杆长为2L，由几何关系，有

x1=m+Lcosα

x2=m-Lcosα

则A点和B点的切线斜率分别为

2a(m+Lcosα)=2am+2aLcosα=k+2aLcosα

2a(m-Lcosα)=2am-2aLcosα=k-2aLcosα

所以AD所在的直线方程为

BD所在的直线方程为

因为AD和BD交于直线x=m上的点，将x=m代入AD和BD的表达式，有

整理后可得

将2am=k及k=tanα代入，整理后有

4a2L2cos2α=tan2α+1

从而

上式给出了杆在抛物面中处于倾斜平衡时，抛物线的形状与杆长L及杆和水平方向的夹角α之间的制约关系．若已知其中的任意两个量，便可根据上式求出第3个量．

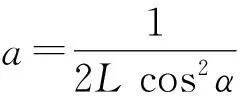
所以抛物线的表达式为

收稿日期：(2015-04-07)