关于两个共点力的合力与两个分力夹角图像的质疑与探究

关于两个共点力的合力与两个分力夹角图像的质疑与探究

王利新

(永吉实验高中吉林 吉林132200)

魏延博

(永吉县教育局吉林 吉林132200)

魏兴文

(永吉实验高中吉林 吉林132200)

摘 要：关于两个共点力的合力与两分力间夹角的图像，在一些教辅图书中常有两种截然不同的形状，究竟孰是孰非，令人困惑不已.本文利用电脑作图及力的图示，从不同角度分析探讨，以辨别正误，正本清源.

关键词：合力变化率拐点

收稿日期：(2014-07-14)

1案例与质疑

1.1案例

案例1:在研究两个共点力合成的实验中得到如图1所示的合力与两个分力的夹角关系图，则这两个分力的大小分别是______N和______N.合力的变化范围为______.

图1

解析:由F-θ图像知,当两分力间的夹角为90°时，合力值为10 N；当两分力夹角为180°时，合力值为2 N.

设两分力分别为F1和F2，且F1>F2，由F-θ图像,可得出当θ=90°时有

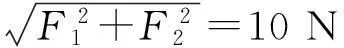
(1)

当θ=180°时有

F1-F2=2 N

(2)

求解式(1)、(2)得

F1=8 NF2=6 N

故两分力的合力F范围为

|F1-F2|≤F≤F1+F2

即

4.培育了现代文明意识大家遵守的融入机制。老旧散不同于商业社区，一般是由农转非形成的“熟人社区”，通过一系列的举措培育社区居民的现代文明意识，能更好的发挥居民自治的参与率和成功率。通过家风家训的征集活动、孝老爱亲典型人物的评比、“二十四孝”文化墙的布置等，培育居民文明意识，回归最真实的自我；通过义工志愿服务、邻里帮扶济困、社区团队活动等，培育助人自助意识，营造邻里一家亲的和谐氛围；通过法治宣传、法治课堂、社区调解队、义务巡逻等，培育居民法治意识，提高法律素养，确保社区长治久安。

2 N≤ F ≤14 N

案例2：如图2所示为两个共点力的合力跟它的两个分力之间的夹角的关系图像，则这两个分力大小分别是

A.1 N和4 N

B.2 N 和3 N

C.1 N 和5 N

D.2 N和4 N

答案：B.

图2

提示：通过图像可知，两力同向时合力大小为5 N，两力反向时合力大小为1 N，从而列式求解，得出2 N和3 N[1].

1.2质疑

上述的案例1和案例2，同样都是两个共点力的合力跟它的两个分力之间的夹角的关系图像，可是它们的F-θ图像却截然不同，虽然图线的形状对求解不会产生影响，但是科学是严谨的，既不能过于随意，更不允许有差错.那么，究竟哪个图正确，还是二者都错，抑或是二者都对？是两个分力的大小造成图像形状的差异，还是与角度的取值范围有关呢？笔者认为很有探究的必要.

2探究与释疑

2.1探究

2.1.1力的图示法

图3是用三角形定则求合力的图示，由此也可直观看出，当θ=0时合力F最大，当θ=180°时合力F最小，且两分力间夹角为0或180°时合力F随θ的变化率最小(为零).在θ从0增大到180°过程中，合力F一直减小，但它对角度的变化率却先增大后减小，在θ从180°增大到360°过程中，合力F一直增大，但它对角度的变化率仍先增大后减小，且当θ=90°和270°时存在拐点.

图3

2.1.2电脑作图法

如图4所示，设分力F1与F2的夹角为θ，则合力

图4

现以案例2为例进行研究，由答案可知F1=2 N，F2=3 N，代入数据得合力

该图像形状究竟如何？现用几何画板分别作出

y1=12cos(x)

y2=13+12cos(x)

图像如图5(a)、(b)、(c)所示.

图5

当然，用描点作图法，同样可以得到图5这样的曲线，只不过繁琐而已.

对比发现，y2相对于y1只是向上平移，但振幅和周期不变.y3相对于y2虽然振幅减小，且形状也不再是标准的余弦曲线(上部丰满，下部苗条)，但是周期和拐点位置仍然不变，且在0～2π范围内于90o和270°两处出现拐点.

有兴趣的读者，利用导数也同样能求出曲线拐点的位置.

2.2释疑

通过以上探究可知，两个共点力的合力与两分力间夹角的图像完整形状(多个周期)应为图5(c)所示，由此可见，图1是正确的，只不过它画出的是90°～270°的部分图线，无可非议.图2画的是0～360°的完整图线，在θ=90°和270°无拐点，故图2似是而非.

类似错误已流传多年，甚至使人习以为常，虽不影响计算结果，但科学是严谨的,绝不允许出现任何纰漏，特别是教辅图书.列· 托尔斯泰曾说过,“认识真理的主要障碍不是谬误，而是似是而非的真理.”

参 考 文 献

1高雪岩,等.尖子生学案· 物理高中必修1(第6版).长春：吉林人民出版社，2011