三体问题一类特解的初探

三体问题一类特解的初探

姜付锦

(武汉市黄陂区第一中学湖北 武汉430300)

摘 要：通过对三体问题的拉格朗日类特解的进一步分析，发现在改变速度初始值情况下存在3类解析解，并用数学软件MathCAD2001对其进行了数值模拟.

关键词：三体问题特解数值模拟

收稿日期：(2014-08-04)

三体问题到目前为止有4组特解：一是3颗等质量天体始终在一条直线上，中间天体不动，其余两颗天体绕中间天体做匀速圆周运动(欧拉类特解)；二是3颗等质量天体组成一个正三角形绕三角形的几何中心做匀速圆周运动(拉格朗日类特解)；三是3颗等质量天体在一个“8字形”轨道上运动(由克里斯-摩尔借助计算机在1993年发现)；四是1颗质量较小的天体在两个质量较大天体的引力场中的运动，两个天体在里面横冲直撞，第3颗天体在它们的外围做环绕运动[1](由布鲁克-赫农借助计算机发现).本文着重对第二类拉格朗日类特解进一步分析，发现了3类解析解.

1建立模型

如图1所示，设3颗天体组成一个正三角形，绕O点做匀速圆周运动，半径为r0,速度为v0.

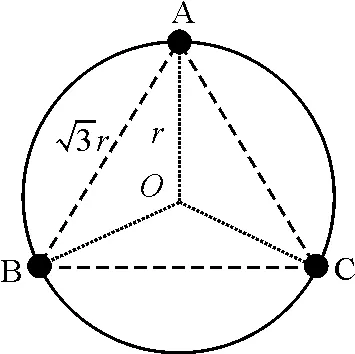
图1　三体组成一个正三角形

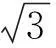
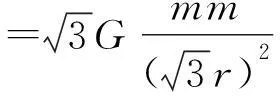
(1)

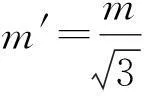
2轨道方程

如图2 所示，取O点为极坐标的极点，根据机械能守恒定律则有[2]

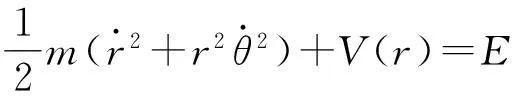
(2)

式中E为天体的总能量，V(r)是系统的引力势能.

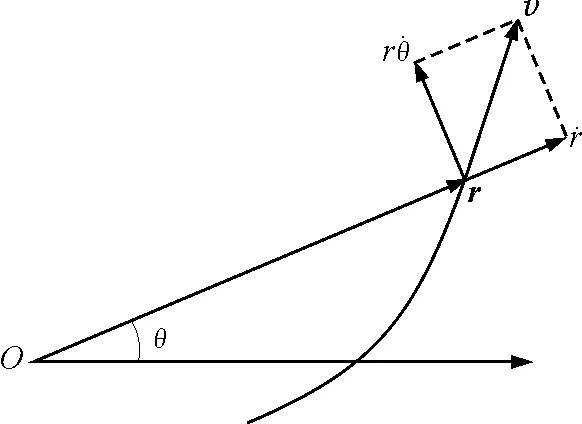
图2　轨道方程

如取无穷远处的势能为零，则质点在距原点r时的引力势能为

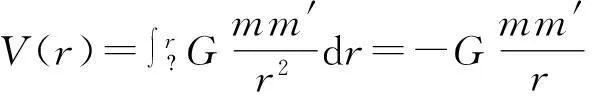
(3)

则式(2)可变为

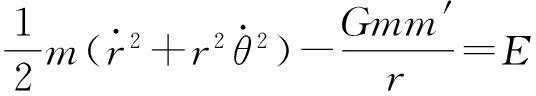
(4)

令

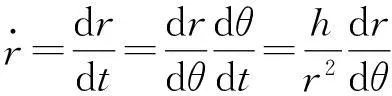
代入式(4)后得

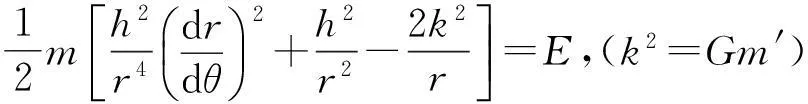
(5)

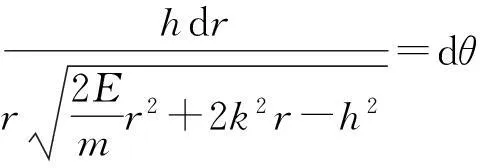
(6)

两边分别积分[3]，得

(7)

故

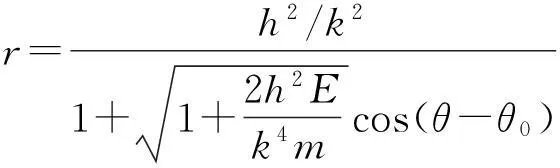
(8)

令

则上式可变为

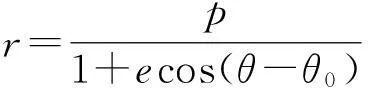
(9)

故天体A的轨道是焦点在原点上的圆锥曲线.

因为A天体的总能量

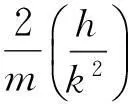
(1)E<0，则e<1，轨道为椭圆.

(2)E=0，则e=1，轨道为抛物线.

(3)E>0，则e>1，轨道为双曲线的一支.

若天体A的轨道为

则天体B的轨道为

天体C的轨道为

当

则

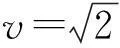
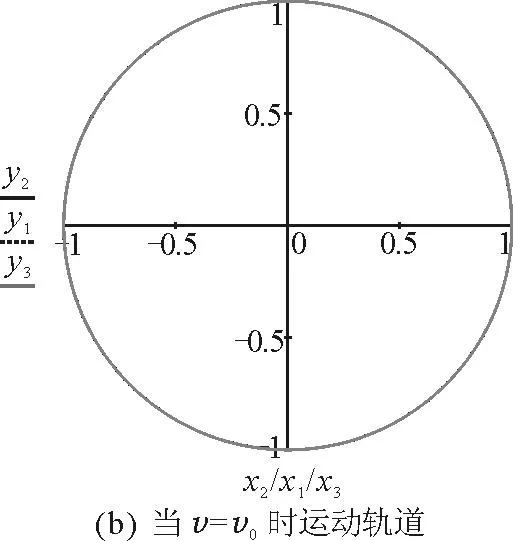
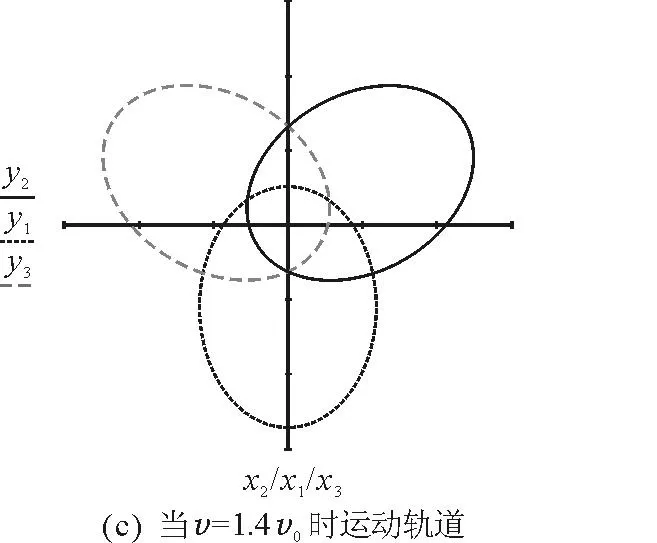
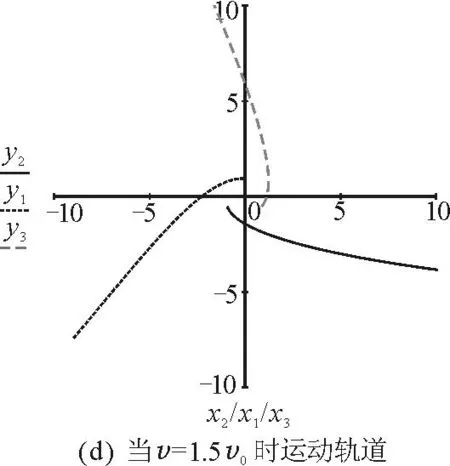
当0

当v=v0时，A天体轨道为圆；

3数值模拟

图3　数值模拟图

4小结

参 考 文 献

1漆安慎，杜婵英.力学(第1版).北京：高等教育出版社，1997.261～264

2周衍伯.理论力学教程(第2版).北京：高等教育出版社，1997.67～74

3周城璧.高等数学(第3版). 北京：高等教育出版社，1997.370～371