双列球型轮毂轴承单元耐久性寿命计算分析

双列球型轮毂轴承单元耐久性寿命计算分析

牛荣军1，李文洒1，康乃正2，汪久根3

(1．河南科技大学 机电工程学院，河南 洛阳 471003；2．浙江兆丰机电股份有限公司，浙江 杭州 311232；3．浙江大学 机电工程系，浙江 杭州 310028)

摘要：对于双列球型轮毂轴承单元数学模型，采用模拟试验载荷谱进行轮毂轴承单元耐久性寿命计算，并分析预紧载荷、侧向加速度和受载偏心距等对球型轮毂轴承单元耐久性寿命的影响。分析结果表明：适当的轴向预紧可提高轮毂轴承单元的刚性以及左右两列轴承的载荷分布均匀性，当轴向预紧量为0.02 mm时，轮毂轴承单元的寿命达到最大值；受载偏心距的影响，使得车辆左右两侧轮毂轴承单元的寿命存在差异，一般驾驶室左侧轴承单元寿命稍高；轮胎半径的大小会同时影响轮毂轴承单元的旋转速度和加载力矩，当轮胎半径取200 mm时轴承单元寿命最长。

关键词：轮毂轴承单元；球轴承；载荷谱；耐久性

基金项目：国家自然科学基金项目(51105131);河南科技大学科研创新能力培育基金项目(2014ZCX004)

作者简介：牛荣军(1977-),男,河南洛阳人,副教授,博士,主要从事滚动轴承设计及理论方面的研究.

收稿日期：2014-04-25

文章编号：1672-6871(2015)01-0013-06

中图分类号：TH133.33

文献标志码：A

0引言

轮毂轴承作为车辆上的关键传动部件，由于其使用工况的复杂性，基于试验载荷谱下的耐久性试验能够对其可靠性和质量做出评价，给出合理寿命预测。试验载荷谱的制定需根据车辆行驶的实际情况，并结合车辆自身的特征，合理、有效的载荷谱是轮毂轴承耐久性模拟试验的一个关键[1]。文献[2-3]开展了基于轿车整车模型的载荷谱理论计算的研究，通过轿车动力性模型的建立，得到作用于轮毂轴承单元的外部载荷；文献[4]以轴承耐久性模拟试验为前提，分析了轿车在各行驶状态下的载荷情况，所制定的载荷谱更贴近于实际轿车的行驶情形；文献[5]以城市路面为轿车的行驶环境，利用传感器测量技术获得轮毂轴承在时域和幅值域的统计图谱。本文参考国内外模拟载荷谱的制定方法，获得作用于轮毂轴承单元的外部载荷谱；然后，基于建立的双列球型轮毂轴承单元与外部载荷的力学平衡方程，通过数值计算方法分析了预紧载荷、侧向加速度、受载偏心距和轮胎半径对轮毂轴承单元综合寿命的影响。

1轮毂轴承耐久性载荷谱

一个完整的耐久性载荷谱应该包括：轮毂轴承的各种旋转状态；轮毂轴承在各种旋转状态下的转速；试验载荷周期变化时间；每个载荷变化周期内的行驶状态时间分配率；各种行驶状态下的载荷。

1.1　轿车载荷变化周期内的行驶参数设置

轿车的行驶状态是由行驶的路面特征和行驶速度来决定的。路面的特征依据线型可以分为直线路面和转向路面；依据行驶路面的环境好坏可分为良好路面和较差路面。NTN轴承公司针对路面的实际特性，提出了一种比较合理的行驶状态模拟，同时引入了载荷冲击因数fw，把良好路面的载荷与较差路面的载荷进行了区分，当轿车在良好路面行驶的载荷为F时，较差路面的行驶载荷便为fwF[6]。

轿车在各种路况下是以一定的车速行驶的，假设轿车的车速为ui，km/h；已知轿车轮胎的滚动半径为Rs，m；能够推导出轮毂轴承耐久性试验的主轴转速ni，r/ min 。

(1)

式中，i=1，2，3，…，代表各种不同的行驶状态。当轿车的各种行驶状态被确定后，则轮毂轴承的试验运行状态也随之确定，进而通过式(1)可以求解出轴承各种运行状态下的主轴转速。

对于轮毂轴承耐久性试验的周期并没有固定的标准。但是很多公司的试验标准能够被借鉴采用，这里采用国外的试验标准[7]120 s。在一个载荷变化周期内，每一种状态需要被赋予一个时间值，每个时间值在一个载荷变化周期总时间内所占的比例被称为时间分配率，具体分配如表1所示。

表1　载荷变化周期内的行驶状态参数

1.2　轮毂轴承外部载荷确定

对于驾驶室右侧轮毂轴承单元，其所受外部载荷如图1所示。根据轮毂结构和受力平衡，可得轮毂轴承单元加载中心处所受载荷：

(2)

式中：Fai为驾驶室右侧地面对轮胎的轴向载荷，N；Fri为驾驶室右侧地面对轮胎的径向载荷，N；Rs为车轮静半径(即车辆静止时车轮中心至地面的距离)；s为车轮受力中心至轮毂轴承中心的轴向偏移距离(简称“偏心距”)；Fr、Fa和M为轮毂轴承所受外部载荷及力矩。根据车辆参数确定左右轮胎的作用载荷后[2]，通过式(2)即可转换出作用于轮毂轴承单元的外部载荷。

2双列球型轮毂轴承单元数学模型

假定外圈固定，两列轴承中心距离为dc，外载荷作用于两列轴承的中心O处，双列球轮毂轴承单元在径向力Fr、轴向力Fa和力矩载荷M作用下，其内、外套圈将产生相对位移δr、δa和θ，如图2所示。

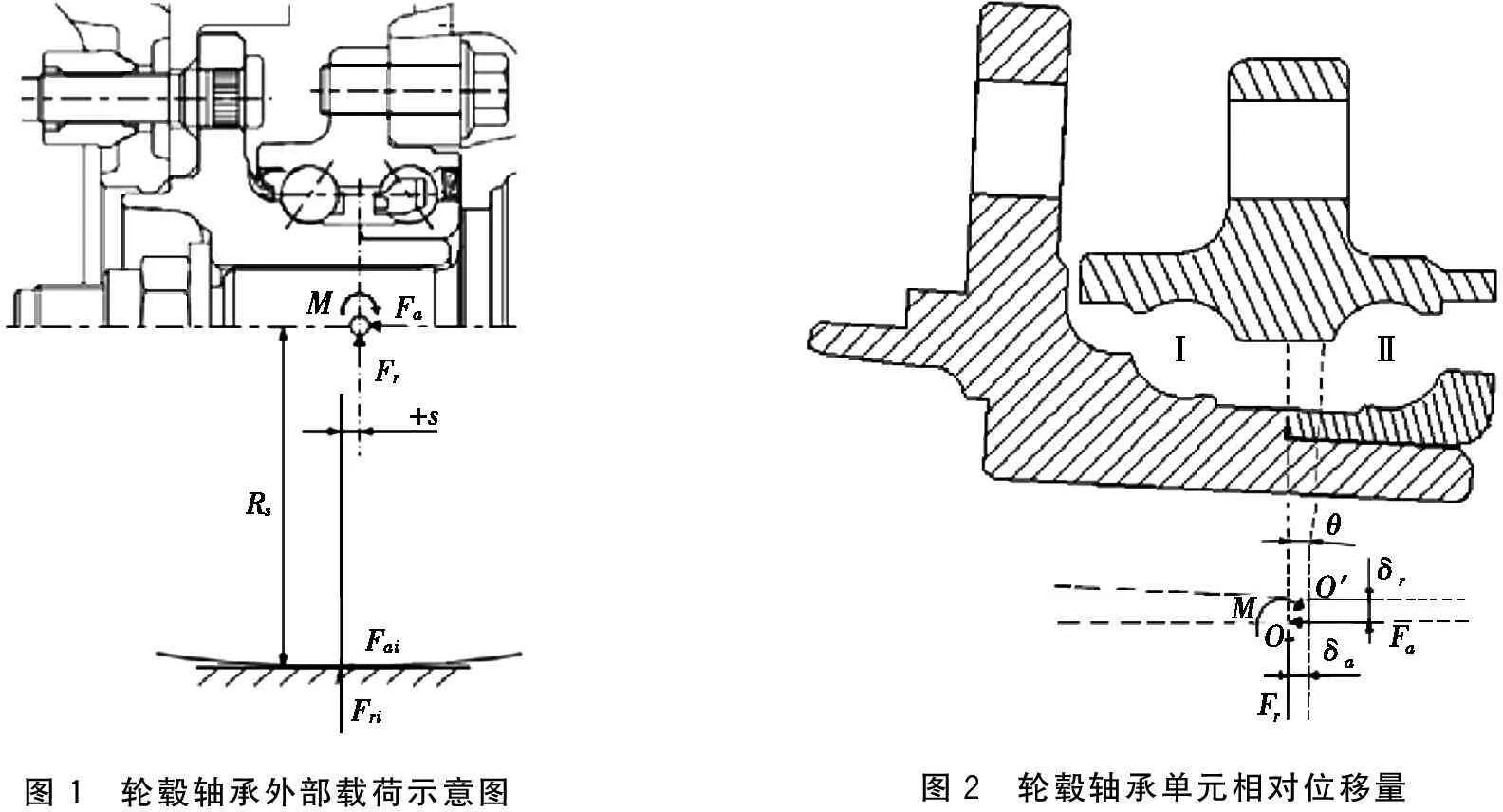
图1 轮毂轴承外部载荷示意图图2 轮毂轴承单元相对位移量

对于驾驶员右侧轮毂轴承单元第I列轴承(见图2)，在位置角为φ的钢球接触处，由δr引起的径向分量为：

δrφ=δrcosφ。

(3)

轴向变形分量相同，都等于δa。由于θ而产生的变形分量可以用图3表示。图3中，Ri是轴承中心O与内圈沟曲率中心Oi之间的距离。根据图3可以得到：

(4)

(5)

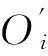
(6)

式中：A0=(ri+re-1)Dw；δ0为由轴向预载荷引起的预变形。

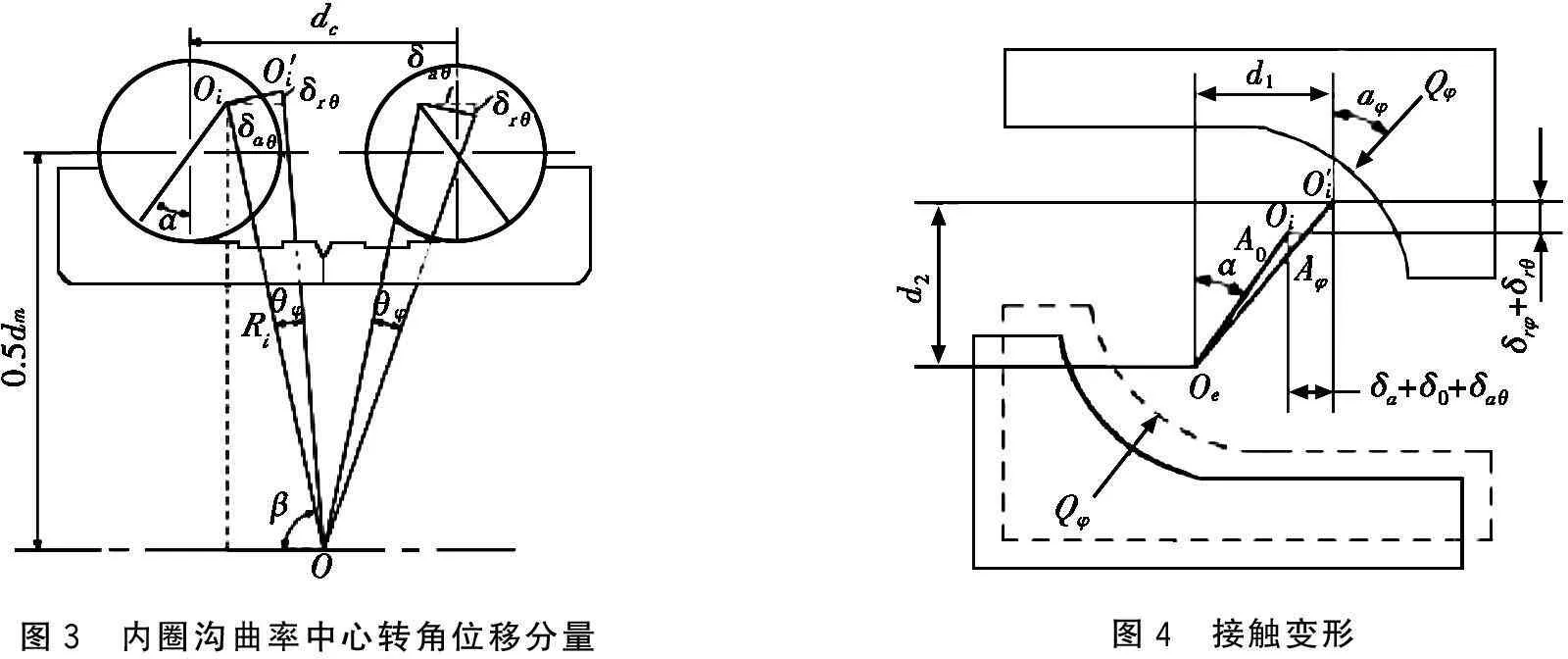
图3 内圈沟曲率中心转角位移分量图4 接触变形

基于Hertz接触理论[8]，可以得到法向接触载荷：

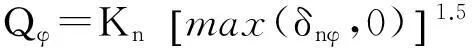
(7)

由法向接触载荷产生的径向力、轴向力分量分别为：

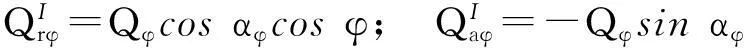
(8)

由径向载荷分量和轴向载荷产生的力矩分量为：

(9)

[0.5dm+Dw(fi-0.5)cosα]Qφsinαφcosφ。

(10)

总的力矩分量为：

(11)

得到轮毂轴承第I列和第II列轴承的径向、轴向和力矩载荷分量后，最终形成的双列球型轮毂轴承单元的整体平衡方程可表示为：

(12)

方程(12)是以δr、δa和θ为未知变量的非线性方程组，可用牛顿迭代法进行求解。

对于所分析轮毂轴承单元，其所受载荷和运转状态在一个试验周期时间(120 s)内要随着行驶状态(良好直线、右转、较差直线和左转)发生变化。当轮毂轴承在当量动载荷Qe1、Qe2、Qe3、…(单位N)作用下，相应转速为n1、n2、n3、…(单位r/min)，运转时各载荷状态下相应时间为t1、t2、t3、…(单位s)，则平均当量动载荷Qem(单位N)可表示为：

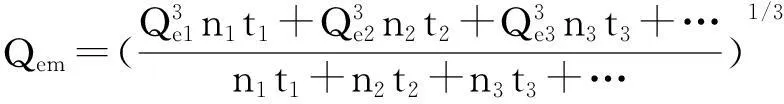
(13)

若轮毂轴承在各种载荷状态下的时间总和为T，在前述对载荷谱的制定过程中给出了轿车每种行驶状态的时间分配率，对应的每种载荷状态下的时间分配率设为q1、q2、q3、…(见表1)，则各种载荷状态所占的时间为：

ti=Tqi，i=1,2,3,…。

(14)

则多工况下，相对于作用载荷的轴承套圈的平均当量动载荷为：

(15)

根据球轴承额定寿命计算方法[10]，分别计算出轮毂轴承单元第I列和第II列轴承的基本额定寿命，然后得到轮毂轴承单元组合轴承的综合寿命为：

L=(LI-10/9+LII-10/9)-0.9。

(16)

将寿命单位由旋转次数转换为时间：

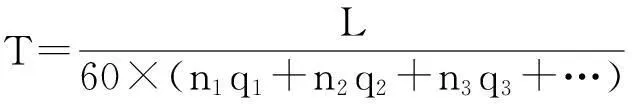
(17)

3结果与分析

在上述双列球型轮毂轴承单元数学模型基础上，对某一轿车用轮毂轴承单元进行不同工况下的寿命分析。用于试验载荷谱计算的轿车参数如表2所示。在试验载荷谱下，可以对轿车前半轴所使用的轮毂轴承单元进行寿命计算，从而分析工况参数变化对轮毂轴承单元寿命的影响。所分析的轮毂轴承单元结构参数如表3所示。

表2　轿车参数

表3　轮毂轴承结构参数

3.1　预紧力对寿命的影响

在轮毂轴承单元装配过程中，适当对轴承单元进行预紧不仅可以提高轴承刚度，而且使得单元中两列轴承承载的滚动体数目增加，提升单元承载能力，从而延长单元的使用寿命。但过大的预紧力将增加轴承的承载载荷，单元寿命下降。因此，在轴承单元装配过程中要合理选择预紧载荷，延长使用寿命。下面将基于轿车较为严格的工况条件，即侧向加速度率fg(侧向加速度ag与重力加速度g的比值)在±0.55工况下，使用表2中轿车参数进行试验载荷谱计算，然后采用式(2)进行载荷转换，可得加载到轮毂轴承单元上的外载载荷谱。驾驶室右侧轮毂单元载荷谱如图5所示。

根据图5中不同工况条件下轮毂轴承单元所受载荷，分析预紧载荷Fa0对轿车前半轴左右两侧轮毂轴承单元综合寿命的影响，如图6所示。由图6可以看出：模拟试验载荷谱条件下，预紧载荷与轮毂轴承单元的寿命呈非线性关系。随着预紧载荷的增加，左右两侧轮毂轴承单元的综合寿命逐渐增加，当达到1.5 kN时，左右两列轮毂轴承单元的寿命达到最大值；然后，随着预紧力的增大，轮毂轴承单元的寿命快速下降。由图6还可以看出：驾驶室左侧的轮毂轴承单元寿命比右侧轴承单元的寿命要长，但随着预紧载荷的增大，两者趋于接近。由上述分析可以得到:对于所分析的轮毂轴承单元，可以在安装时通过预紧螺母进行载荷预紧，使得作用于左右两列轴承上的预紧载荷在1.5 kN左右，左右两列轴承形成的轴向预紧量为0.02 mm，此时可使得在图5的载荷谱下，轮毂轴承单元达到最大使用寿命。

图5　一个周期内驾驶室右侧轮毂轴承载荷谱

3.2　侧向加速度对寿命的影响

轿车在行驶过程中，在急转弯时会形成较大的侧向加速度ag，一般情况下在0.4倍的重力加速度左右，并且作用时间很短。但此时，由于轮胎半径Rs和受载偏心距s的影响将形成很大的力矩载荷M。在力矩载荷作用下，轮毂轴承单元的当量动载荷增大，从而使得轴承单元的寿命明显下降。图7给出了侧向加速度率fg与轮毂轴承单元寿命的关系曲线。由图7可以看出：随着侧向加速度率的增大，轮毂轴承单元的综合寿命明显下降，特别是在0.2～0.7，寿命下降较快，而在其他区间下降较缓。此外，随着侧向加速度率的变化，驾驶室左右两侧轮毂轴承单元的寿命相差发生变化，其中，在0.5时相差最大(1.5×103h)，整体上驾驶室左侧轮毂轴承单元寿命高于右侧轴承单元的寿命。

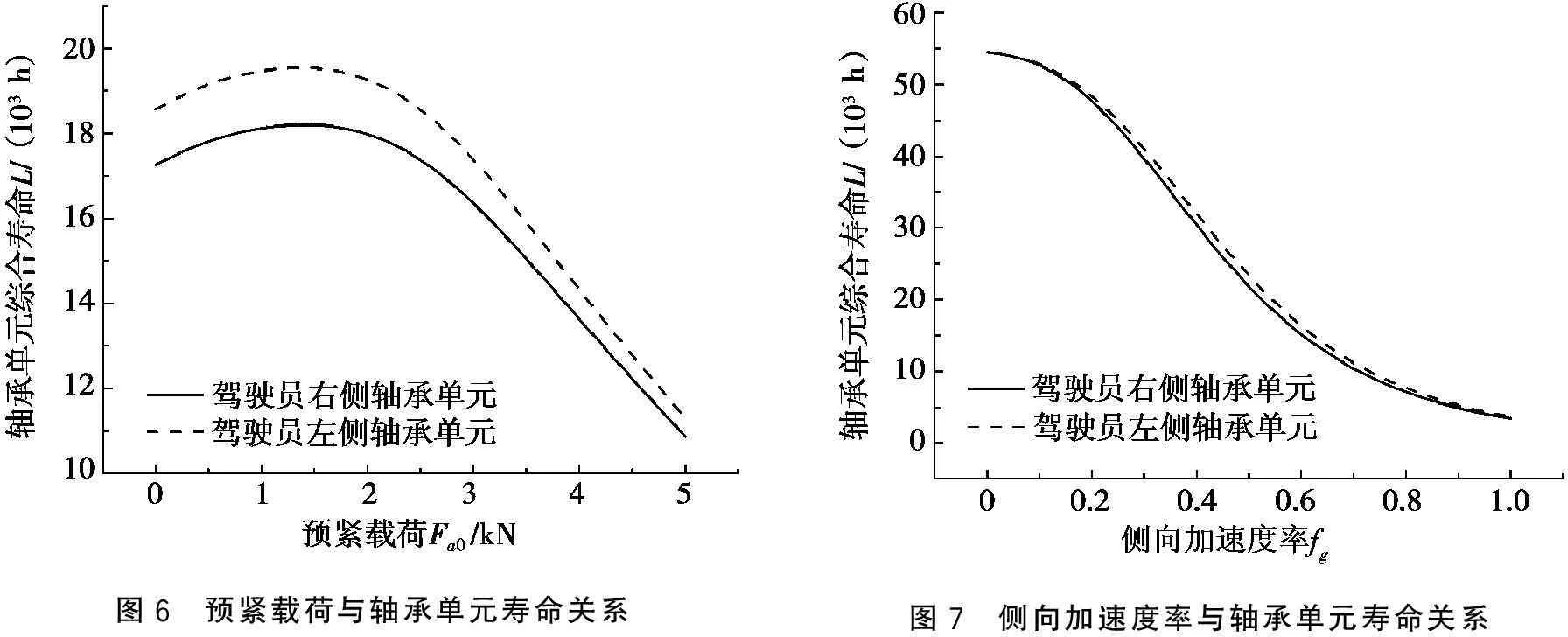
图6 预紧载荷与轴承单元寿命关系图7 侧向加速度率与轴承单元寿命关系

3.3　受载偏心距对寿命的影响

在轮毂轴承单元设计和装配时，轮毂轴承单元的受载中心与轮胎承载中心存在一个偏心距s(见图1)，此偏心距的存在使得轮毂轴承单元承载一个附加力矩作用，使得轴承单元两列滚动体载荷分布发生变化，从而影响轮毂轴承单元的寿命。图8为偏心距位置变化对轴承单元寿命影响关系曲线。由图8可以看出：偏心距s为零时，驾驶室左右两侧轮毂轴承单元的综合寿命相同;但当偏心距为正向增加(如图1所示)时，驾驶室右侧轴承单元寿命下降，左侧上升；当偏心距负向减小时，变化趋势刚好相反。从分析结果来看，当偏心距为零时最好，但实际轮毂轴承单元，特别是第3代轮毂轴承单元，其芯轴和外圈上都通过法兰盘结构与其他部件进行连接，受载时法兰盘的柔性支撑作用使得轴承单元的承载中心发生偏移。因此，实际设计时将轮毂轴承单元的受载中心与轮胎的承载中心设计一定的偏移量。

3.4　轮胎半径对寿命的影响

在轮毂轴承单元设计时，首先要确定轴承所使用的车辆类型和工况条件。在获得车辆参数后，设计试验载荷谱对轮毂轴承单元进行模拟试验。因此，其力矩半径，即车辆参数轮胎半径Rs应该首先确定。但实际模拟试验过程中，为了对轮毂轴承单元进行加速试验，一般采用增大力矩半径方法进行试验。基于试验载荷谱进行轴承综合寿命的计算可知:随着轮胎半径的变化，轮毂轴承单元的转动速度随之发生变化。图9为不同轮胎半径对轴承单元综合寿命的影响。由图9可以看出：当轮胎半径为200 mm左右时，基于试验载荷谱得到的左右两侧轮毂轴承单元的综合寿命最大，而在其他区间则快速下降。其中，在100～200 mm时寿命下降，主要是由于轮毂单元转速升高对寿命产生的影响；而在100～450 mm时寿命下降，主要是由于力矩载荷增大对寿命产生的影响。根据分析结果，对于所设计的轮毂轴承单元，使用车辆的轮胎半径取200 mm左右较合适。

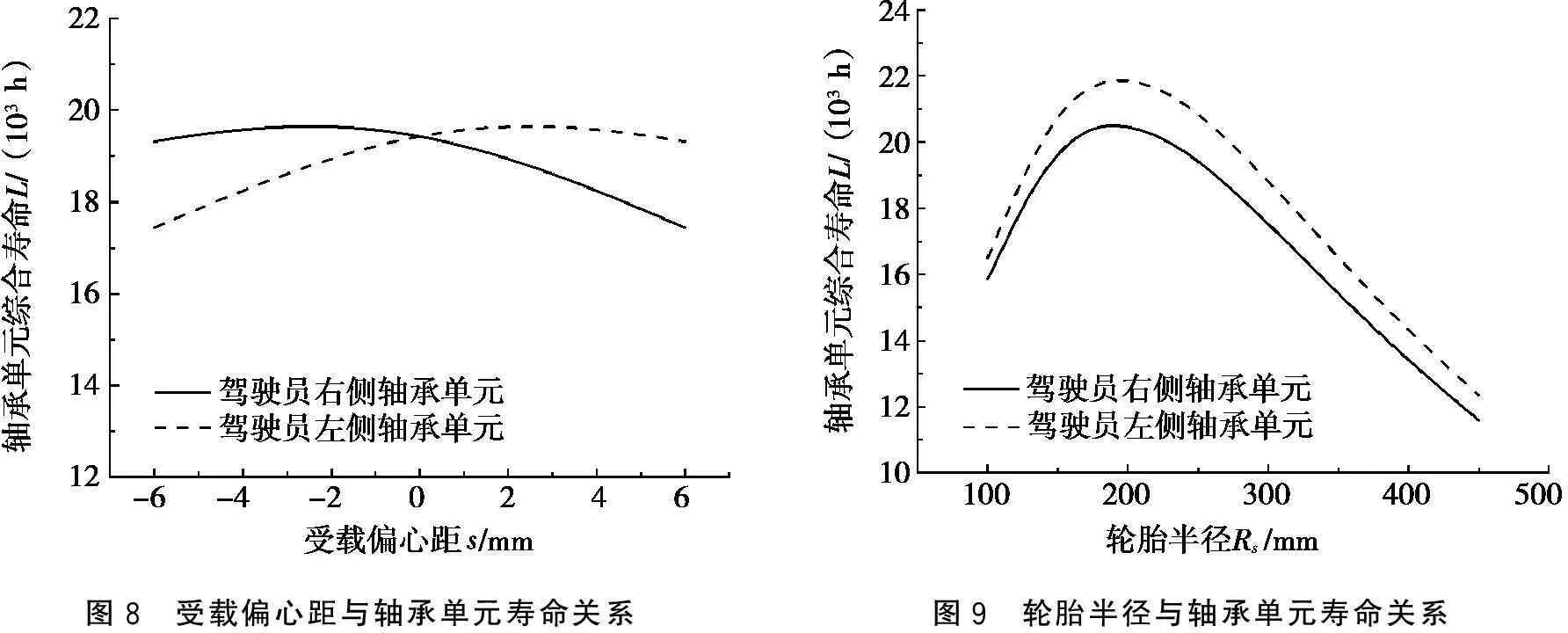
图8 受载偏心距与轴承单元寿命关系图9 轮胎半径与轴承单元寿命关系

4结论

(1)由于轮毂轴承单元使用工况的特殊性，对其进行寿命分析时要合理设计试验载荷谱，从而较准确预测轮毂轴承单元的综合寿命。

(2)适当的轴向预紧可提高轮毂轴承单元的刚性以及左右两列轴承的载荷分布均匀性，从而延长轴承单元寿命。对于所分析轮毂轴承单元，当轴向预紧量为0.02 mm时，轮毂轴承单元的寿命达到最大值。

(3)受载偏心距的影响，使得车辆左右两侧轮毂轴承单元的寿命存在差异，一般驾驶室左侧轴承单元稍高。并且在轴承单元设计时应考虑法兰盘的柔性变形影响，合理设计受载偏心距。

(4)轮胎半径的变化对轮毂轴承单元的旋转速度和加载力矩都会产生明显影响，对于所分析的轮毂轴承单元，其所应用车辆的轮胎半径取200 mm左右较合适。

参考文献：

[1]NSK中国技术中心.轮毂轴承的发展趋势和最新技术[J].轴承,2007(3):46-50.

[2]黎桂华,黄平,赵联春,等.轿车轮毂轴承外部载荷计算方法及其特性[J].润滑与密封,2006(11):17-20.

[3]黎桂华,李兴林.轿车轮毂轴承耐久性试验载荷谱设计[J].轴承,2006(1):27-28.

[4]黄德杰.轿车轮毂轴承耐久性计算与试验系统开发[D].杭州:浙江工业大学,2010.

[5]张雪萍,陈以农.轿车轮毂轴承城市道路载荷谱测试与分析[J].上海交通大学学报,2001(12):1813-1816.

[6]牛辰.第三代轮毂轴承单元温度场分析和寿命估算[D].洛阳:河南科技大学，2014.

[7]董晓.汽车轮毂双列角接触球轴承动力学仿真分析[D].洛阳:河南科技大学,2014．

[8]Harris T A.Rolling Bearing Analysis[M].4 ed.New York:John Willey & Sons,Inc,2001.

[9]李开元,俞水良,张柏松,等.轮毂轴承单元接触应力的数值计算与分析[J].轴承,2011(10):1-4.

[10]GB/T 6391—2010滚动轴承额定动载荷和额定寿命[S].北京:中国标准出版社,2011.