电梯系统共振失效的灵敏度研究

电梯系统共振失效的灵敏度研究

冯文周1,2,3，曹树谦1,2，赵峰1,2，胡铖4，刘文波3

(1.天津大学机械工程学院力学系，天津300072；2.天津市非线性动力学与混沌控制重点实验室，天津300072；3.奥的斯电梯(中国)有限公司，天津300457；4.大连理工大学机械工程学院，辽宁大连116024)

摘要：以曳引式电梯为研究对象，考虑电梯曳引绳刚度具有时变特性，对电梯系统建立了8自由度耦合振动的动力学模型。在对系统进行模态分析的基础之上，以影响系统模态频率的动力参数作为随机变量，结合DOE试验方法与神经网络技术，得出系统随机变量与系统模态响应之间的显性函数关系式。依据动态结构系统的固有频率与激振频率差的的关系准则，定义了系统共振的失效模式，并对系统的随机变量进行了可靠性灵敏度分析。研究表明，绳头侧刚度和曳引机支撑刚度对频率共振影响最为明显，因此，在电梯系统设计中可以通过修改该动力参数达到有效降低共振的风险。同时，在实际工作中应该严格关注和监视该动力参数的变化，避免发生共振。

关键词：电梯振动；共振；失效灵敏度；神经网络

中图分类号:TU857文献标志码：A

基金项目：国际科技合作项目：镁质车体前端设计开发及NVH特性研究(2007DFB50150-2)

收稿日期：2013-04-16修改稿收到日期：2013-11-06

Resonancefailuresensitivityforelevatorsystem

FENG Wen-zhou1,2,3, CAO Shu-qian1,2, ZHAO Feng1,2, HU Cheng4,LIUWen-bo3(1.TianjinUniversity,Tianjin300072，China； 2.Tianjinkeylaboratoryofnonlineardynamicsandchaoscontrol,Tianjin300072，China;3.Otiselevator(China)corporationlimited,Tianjin, 300457，China; 4.DalianUniversityoftechnology,LiaoningDalian116024，China)

Abstract:Taking the traction type elevator as the research object, and considering the time-varying characteristics of traction rope stiffness when the elevator is in normal working condition, an eight degrees of freedom dynamic model of coupled vibration was established for studying the vertical vibration characteristics of the elevator system and the effect of sensitivity of natural frequency on the vibration of elevator system. On the basis of modal analysis on the elevator system, dynamic parameters impacting on the system modal frequency were selected as random variables. Combining the design of experiment (DOE) test method and artificial neural network (ANN) technology, an explicit function was obtained between each random parameter and the modal response of elevator system. According to the criterion that the absolute value of the difference between the natural frequency of the dynamic structure system and the excitation frequency should not be in excess of an allowance, the failure mode of system resonance was defined, and the reliability sensitivity of the elevator system was studied. The results reveal that the termination stiffness of the traction rope and the isolation pad of traction machine are prominent factors for system resonance. In practice, the risk of resonance can be mitigated effectively by modifying these parameters. Simultaneously, the changes of these dynamic parameters should be strictly monitored to prevent resonance in working process.

Keywords:elevatorvibration;resonance;failuresensitivity;artificialneuralnetwork

由于高层建筑的不断增多，电梯正在朝着高速度、高载重、高扬程的方向发展。在高速度、高扬程工况下的电梯轿厢的振动特性更加明显，因此，其运行过程中的安全性和舒适性越来越受到人们的重视,对于电梯系统的振动特性的研究已经成为电梯行业研究热点。

国内外学者关于电梯振动的研究主要集中在机械和电气两方面[1-6]。机械振动主要是由曳引机、承重装置、悬挂装置、轿厢结构设计不良，导轨质量、制造安装误差等方面所致；电气方面主要是由电动机、编码器回路、控制系统性能等方面引起的。在工程实际中电梯系统因各零部件配置不同，所表现出材料性能参数具有随机性。因此，研究电梯系统随机结构的分析远比确定性结构更具有意义。在进行随机结构的性能分析时，由于各因素对结构系统的响应的敏感度是不同的，因此对于系统的灵敏度分析具有重大意义。目前对于结构可靠性灵敏度分析主要有基于矩方法的可靠性灵敏度分析和MonteCarlo方法的数值模拟方法[7]。当电梯激励频率与电梯系统的某阶固有频率较近时，电梯就会发生共振，这是电梯振动失效的一种比较常见的现象。因此，对于电梯系统固有特性的研究显得极为重要。目前，针对电梯系统振动力学模型研究较多[8-12]，但是在研究内容和研究方法上都需要完善。基于此背景下，本文在对电梯系统的8自由度耦合振动分析的基础上，定义了电梯系统共振失效的数学模型，结合可靠性灵敏度分析方法对电梯系统各随机参数进行了灵敏度分析，本方法可以作为指导电梯系统设计和减振分析的理论依据。

1动力学模型的建立

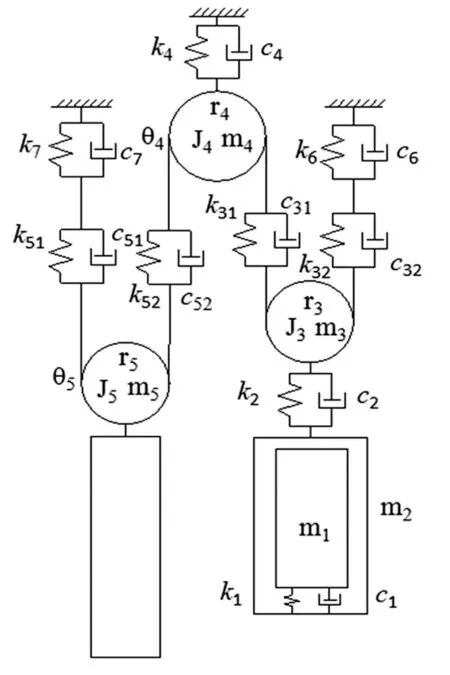
图1　电梯系统动力学模型 Fig.1 The dynamic model of elevator system

以绕绳比2∶1曳引式电梯为研究对象，电梯的机械系统主要包括轿厢、悬挂装置、曳引绳、曳引机、对重以及补偿链等组件。通过对电梯系统零部件的简化，对电梯系统建立如图1所示8自由度的动力学模型，其中曳引轮为系统的主动轮，一般情况下，曳引机与曳引轮是刚性联接，因此曳引轮的转动刚度为零，系统将会出现刚体模态。动力学模型中m1、m2、m3、m4、m5分别为轿厢、轿架、轿厢侧、反绳轮、曳引机、对重的等效质量。J3、r3为轿厢侧反绳轮的转动惯量和回转半径，J4、r4为曳引轮的转动惯量和回转半径，J5、r5为对重反绳轮的转动惯量和回转半径。k1、c1为轿厢与轿架之间的刚度和阻尼，k2、c2为轿架与轿厢侧反绳轮之间的刚度和阻尼。k3i、c3i和k5i、c5i分别为轿厢侧曳引绳的刚度、阻尼和对重侧曳引绳的刚度和阻尼。(i取1表示左边曳引绳，i取2表示为右侧曳引绳)。k4、c4为曳引机隔振垫的等效刚度和阻尼。k6、c6为轿厢侧绳头弹簧的刚度和阻尼，k7、c7为对重侧绳头弹簧处的刚度和阻尼。

2电梯系统的振动微分方程

由动力学模型可知，该系统为8自由度的振动系统。令x1，x2，x3，x4，x5分别为m1，m2，m3，m4，m5的线位移，垂直向上为正，θ3，θ4，θ5分别为m3，m4，m5的角位移，逆时针方向转动为正。根据拉格朗日第二类方程[13]建立系统的振动微分方程。

(i=1,2,…,n)

(1)

(2)

(3)

式中，k31与k52的刚度与轿厢在井道中位置有关，由式(4)~(5) 决定，k3e,k5e分别为轿厢侧曳引绳与绳头弹簧的串联刚度和对重侧曳引绳与绳头弹簧的串联刚度。由式(6)~式(7) 决定

k31=k32=NEA/(H+h-x1)

(4)

k51=k52=NEA/(h-x1)

(5)

(6)

(7)

(8)

式中，N、E、A分别表示曳引绳个数、弹性模量和截面面积，H表示提升高度，h表示轿厢在顶层时轿厢反绳轮中心到机器曳引轮中心的垂直距离。q表示系统的平衡系数，D表示额定载重量。将式(2)～式(8)代入式(1)得出系统振动的微分方程,写成矩阵形式如下:

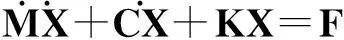
(9)

式中，X={x1, x2, x3, x4, x5,θ3,θ4,θ5}T表示系统的位移向量，M、K、C分别为系统的质量矩阵、刚度矩阵和阻尼矩阵。

3共振失效的灵敏度分析

由离散结构体组合的系统发生共振时，各离散体的振幅均达到最大，当所关注的结构体的振幅超过槛值，结构系统处于失效状态或准失效状态。通过对系统失效状态进行灵敏度分析，得出影响系统失效的敏感因子，利用动力修改技术修改结构的敏感因子如质量、刚度、阻尼等，使结构系统满足设计上规定的要求。根据可靠性的应力强度干涉理论，具有随机结构参数的电梯系统其共振失效的状态函数为：

i=1,2,…,n,j=1,2,…,m

(10)

式中，fi为系统外载荷的第i个激振频率，ωj为系统的j阶固有频率。

根据激振频率和系统固有频率的关系准则，可以确定结构发生共振失效的极限状态函数。

(11)

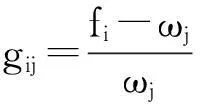
(12)

一般情况下系统结构的随机参数都不是固定值，而是服从特定的分布类型。如果想精确确定系统随机参数的实际分布类型，就需要大量的实验数据进行统计学分析，这给分析带来了困难，工程实际中，随机变量以正态分布最为典型，这也是在工程分析中首选的分布类型。则系统共振失效的概率为

(13)

式中Φ(•)表示标准的正态分布，μgij和σgij和分别表示Gij的均值和标准差，即

μgij=E(gij)=E(fi)-E(wj)

(14)

(15)

在结构系统中，只要激振频率接近系统中任一阶固有频率时，都会使整个系统发生共振。 因此，当系统具有多阶固有频率或者具有多个激振频率时，系统可靠性的分析结构模型为串联系统。依据串联系统的可靠性分析理论[14]，得出系统的失效概率。

(16)

式中:R表示系统的可靠度。根据可靠性灵敏度的定义，可靠度R对各基本随机参数的B={k1,k2,k4,k6,k7,m1,m2}T的均值灵敏度和方差灵敏度分别定义为

(17)

(18)

式中:βuv1、βuv2为可靠性指标，定义为

(19)

(20)

4数值算例

以工程中实际电梯模型为研究对象，分析电梯系统空载情况下在井道中运行的情况。曳引机的工作转

速为662r/min，即系统的激励频率为11.03Hz，由模态理论可知[15]，阻尼系数对系统的固有频率影响较小，一般可以不予考虑。由于电梯运动过程中k3i和k5i具有时变特性，故电梯系统的各阶固有频率也具有时变特性。本算例中电梯的额定载重D为1 000kg,平衡系数q为0.475，则对重等效质量m5按照式(8)给出。

因此，由式(1)～(9)通过Matlab运用数值分析方法进行模态分析，得出系统的各阶固有频率，图2、图3分别为轿厢位移x1与固有频率ω1-ω4和ω5-ω8的变化曲线。

图2 前四阶固有频率变化曲线Fig.2Thefirstfourorderofnaturalfrequenciescurve图3 5-8阶固有频率曲线Fig.3Fivetoeightorderofnaturalfrequenciescurve图4 BP神经网络训练误差Fig.4BPneuralnetworktrainingerror

通过图3曲线可以看出当轿厢位于到40m位移处，系统的固有频率ω5和ω6与激振频率最为接近，易发生共振。因此，轿厢位移为40m时计算系统的固有频率，如表1。

表1　轿厢在40 m位移时电梯系统垂直振动的固有频率

电梯系统的固有频率与系统的动力参数相关，因此，有必要分析动力参数的变化对系统共振失效的敏感程度。根据经验选择电梯系统本身可控的参数作为随机变量，分别是轿厢与轿架之间的刚度k1，轿架与反绳轮之间的刚度k2，曳引机隔振垫的刚度k4，轿厢侧绳头弹簧的刚度k6和对重侧绳头弹簧处的刚度k7，以及轿厢质量m1，轿架质量m2。 基于随机变量的振动微分方程，利用Matlab不能直接得出随机变量B={k1,k2,k4,k6,k7,m1,m2}T与固有频率ω5和ω6的显性函数表达式。因此本文采用优化软件ISIGHT集成Matlab编制的程序进行循环分析，选择超立方拉丁抽样方法对随机变量B={k1,k2,k4,k6,k7,m1,m2}T进行抽样64次，将其作为BP神经网络训练的样本，将每次分析的结果作为BP神经网络的响应值。通过神经网络训练后，可以拟合出随机变量与ω5和ω6之间的显性函数关系式。假设随机变量符合正态分布，均值和标准差取值如下。

经过86次训练后，由训练后的神经网络模型得出的响应值与ω5的理论值之间的误差精度达到10-6，如下图4所示。

为了确保神经网络拟合出的函数的准确性，对随机参数按照正交试验方法抽样20次进行验证，并与Matlab编制的振动微分方程求得的理论值结果进行比较，检验结果如图5所示，说明了神经网络模型是可靠的。

同理，对随机变量与模态频率ω6进行函数拟合，经过275次训练，由训练后的神经网络模型得出的响应值与ω6的理论值之间的误差精度达到10-7，如图6所示。并将随机参数代入训练后的神经网络模型得出ω6响应与理论数值计算的结果进行比较，如图7所示，可以得出神经网络拟合的函数代替理论模型是可靠的。

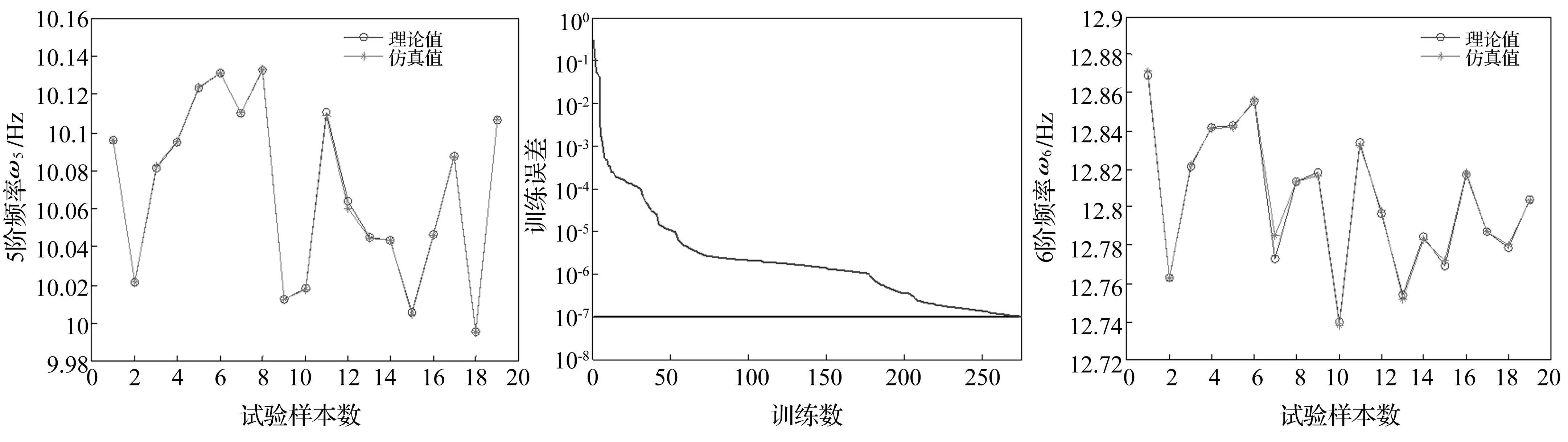
图5 均值处随机样本模拟检验图Fig.5Randomsamplingsimulationtestinmean图6 BP神经网络训练误差Fig.6BPneuralnetworktrainingerror图7 均值处随机样本模拟检验图Fig.7Randomsamplingsimulationtestinmean

将神经网络拟合后的函数，代入式(10)～(16)，得出系统的准失效概率Pf=0.981，由此可知，系统发生共振失效的可能性极大。代入式(17)～(20)对其进行灵敏度分析，得出可靠度对随机变量均值的灵敏度为

可靠度对随机变量方差的灵敏度为

因为随机变量的单位不全相同，为了便于比较各参数的敏感程度，须将随机变量可靠度的灵敏度进行无量纲化[16]，无量纲化后的均值灵敏度αs和方差灵敏度ηs定义为

(21)

(22)

式中，σs*，Var(Bs)*分别为基本随机变量Bs的标准差和方差，R*为系统的可靠度，将均值灵敏度和方差灵敏度的结果分别代入式(21)和(22)，得到可靠度对各随机变量均值灵敏度αs和方差灵敏度ηs排序如图8和图9所示。

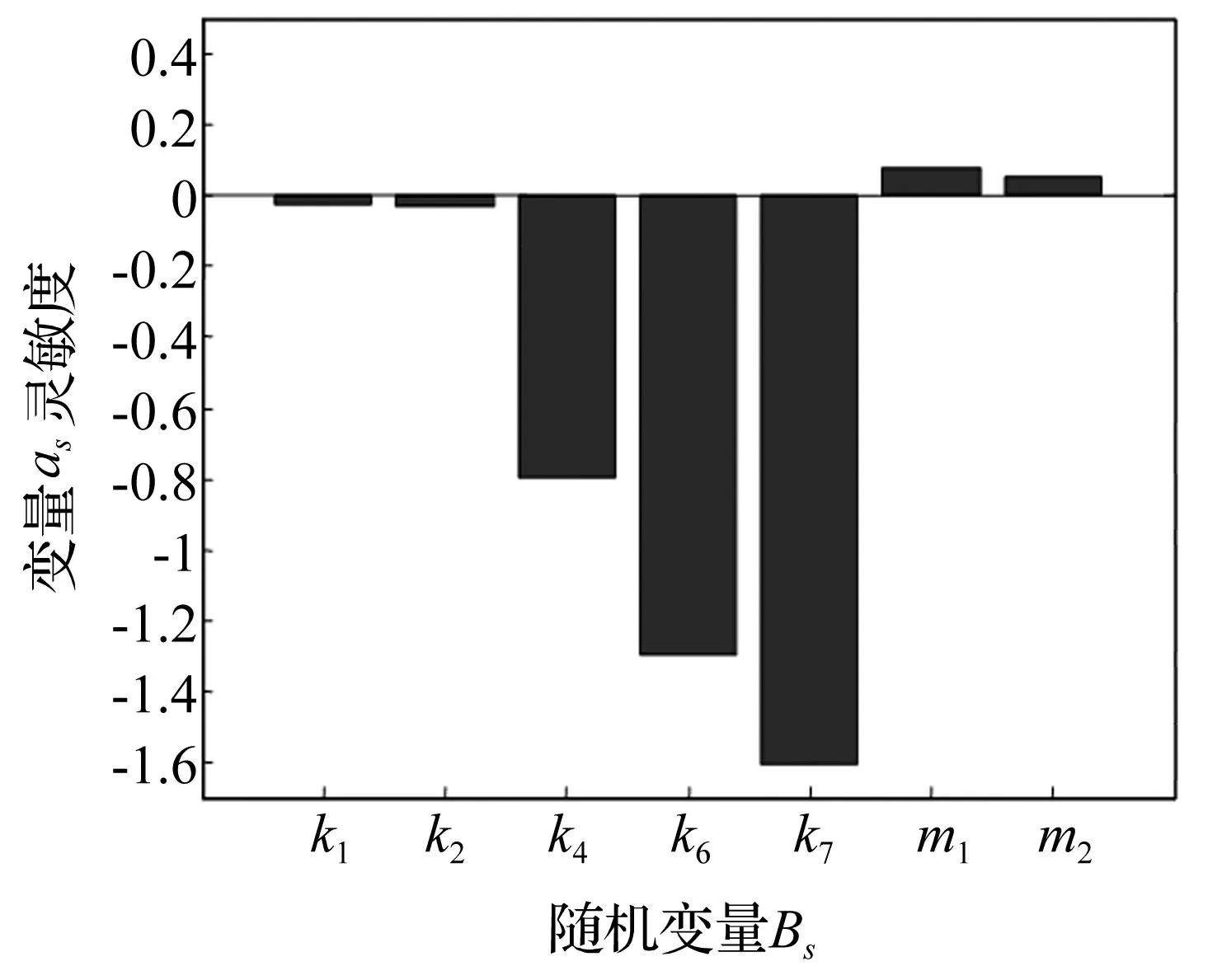
图8　可靠度对基本随机变量均值灵敏度 Fig.8 The sensitivity of mean of basic random variable for reliability

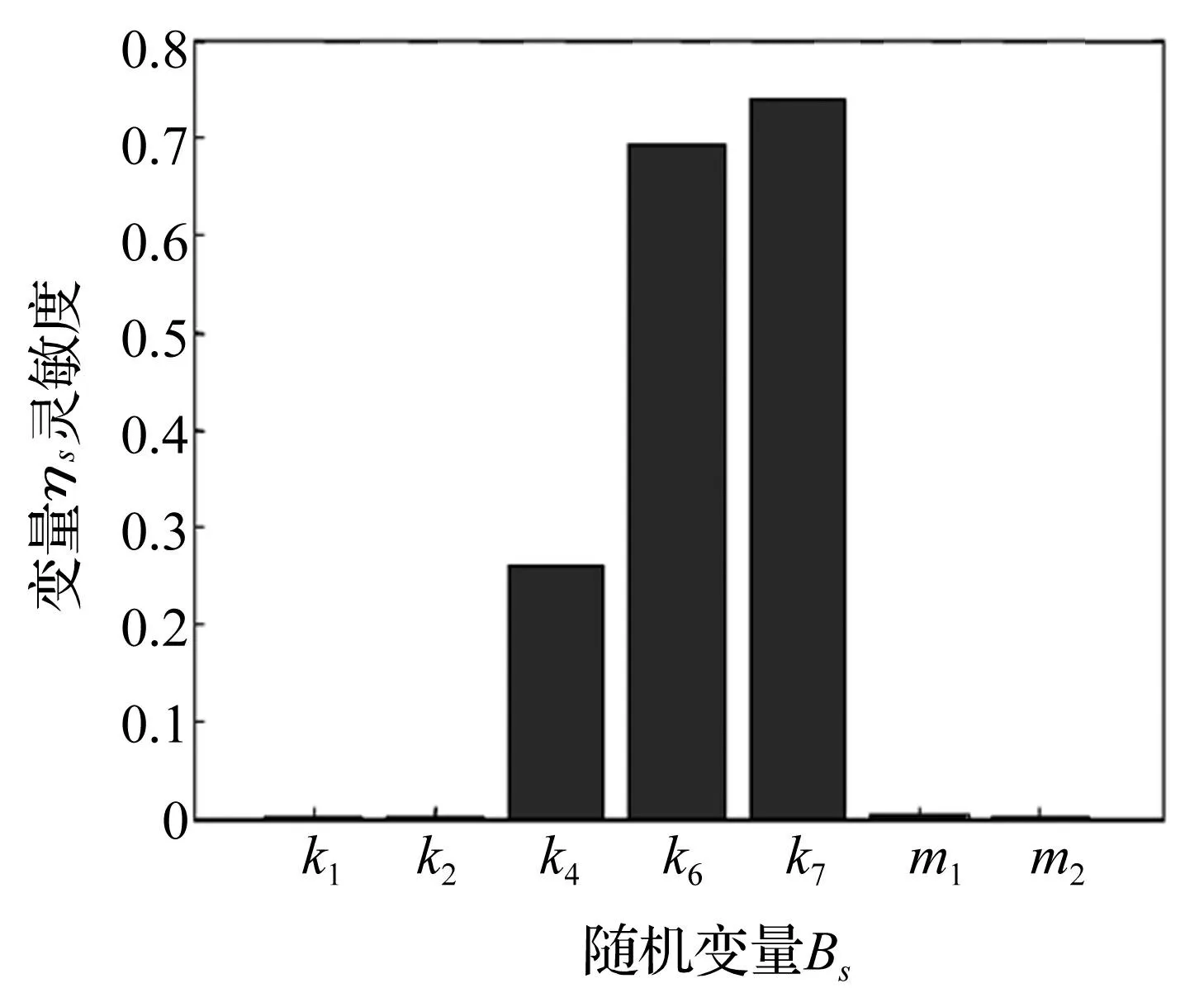
图9　可靠度对基本随机变量方差灵敏度 Fig.9 The sensitivity of variance of basic random variable for reliability

通过灵敏度分析的结果表明，不同随机参数对系统可靠性的影响程度是不同的。对于本电梯系统来说，电梯系统随机参数m1、m2的增加会使系统趋于更加可靠，而随机变量参数k1、k2、k4、k6、k7的增加会使系统趋于不可靠。其中k4、k6、k7较为敏感，其他随机变量影响不大。因此，为了有效降低共振的影响，在设计时要重点关注绳头弹簧刚度和曳引机的隔振垫的刚度。

5结论

(1)对曳引式电梯系统建立8自由度耦合振动动力学模型，并考虑了电梯轿厢两侧曳引绳在轿厢运行过程中具有变刚度特性，得出的各阶固有频率也具有时变特性。通过各阶频率曲线可以看出轿厢位置对各阶频率影响不同。

(2)本文将频率可靠性灵敏度相关理论应用到电梯系统振动的可靠性问题上，结合人工神经网络技术和模态分析方法，对电梯系统共振失效进行了灵敏度分析，研究结果表明系统的一些参数对共振失效的影响较大，在结构参数设计时具有指导意义。

参考文献

[1]KangJK,SulSK.Vertical-vibrationcontrolofelevatorusingestimatedcaraccelerationfeedbackcompensation[J].IEEETransactionsonIndustrialElectronics(S0278-D046), 2000, 47(1):91-99.

[2]NaiK,ForsytheW,etal.Improvingridequalityinhigh-speedelevators[J].ElevatorWorld, 1997(6):88-93.

[3]YamazakiY,TomisawaM,etal.Vibrationcontrolofsuperhighspeedelevators[J].ProcoftheIMAC,1998 :300-306.

[4]于德介，喻进辉. 高速电梯机械系统动力学模型的建立与修正[J]. 振动与冲击,1997(1):11-14.

YUde-jie,YUjin-hui.Establishingandupdatingthedynamicmodelofthemechanicalsystemofhighspeedelevators[J].VibrationandShock,1997(1):11-14.

[5]胡振东，赵珊珊.高速电梯系统时变动力学模型与分析[J].力学季刊,2002,23(3):422-426.

HUZhen-dong,ZHAOShan-shan.Modelingandanalysisoftime-varyingdynamicsforhigh-speedelevator[J].ChineseQuarterlyofMechanics,2002,23(3):422-426.

[6]包继虎，张 鹏，朱昌明.变长度提升系统钢丝绳纵向振动特性[J].振动与冲击,2013,32(15):173-177.

BAOJi-hu,ZHANGPeng,ZHUChang-ming.Longitudinalvibrationofropehoistingsystemswithtime-varyinglength[J].JournalofVibrationandShock,2013,32 (15):173-177.

[7]MelchersRE,Ahammedm.AfastapproximatemethodforparametersensitivityestimationinMonteCarlostructuralreliability[J].Computers&Structures, 2004, 82(1):55-61.

[8]张长友，朱昌明.电梯系统动态固有频率计算及减振策略[J].系统仿真学报,2007, 19(16):3856-3859.

ZHANGChang-you,ZHUChang-ming.Calculationmethodofdynamicnaturalfrequenciesofelevatorsystemandvibration-suppressionstrategy[J].Journalofsystemandsimulation, 2007, 19(16):3856-3859.

[9]罗永彬，陈炳炎，朱光汉.电梯机械系统动态特性分析[J].浙江工业大学学报，1997, 3(25):211-217.

LUOYong-bin,CHENBing-yan,ZHUGuang-han.Analysisofthedynamicbehaviorofelevatormechanicalsystem[J].JournalofZhejiangUniversityofTechnology,1997, 3(25):211-217.

[10]付岑.电梯振动的试验分析与解决方案[J].起重运输机械，2001(8):19-21.

FUCen.Testanalysisandsolutionforelevatorvibration[J].HoistingandConveyingMachinery,2001(8):19-21.

[11]张聚，杨庆华,周国斌,等.高速电梯机械系统振动的分析与计算[J].机电工程,2000, 17(4):78-82.

ZHANGJu,YANGQing-hua,ZHOUGuo-bin,etal.Vibrationanalysisandcomputationofmechanicalsystemofhigh-speedelevator[J].Mechanical&ElectricalEngineeringMagazine, 2000, 17(4):78-82.

[12]张长友，朱昌明，吴光明.电梯系统垂直振动分析与抑制[J].振动与冲击，2003, 22(4):72-75.

ZHANGChang-you,ZHUChang-ming,WUGuang-ming.Suppressionandanalysisontheverticalvibrationofelevatorsystem[J].JournalofVibrationandShock, 2003, 22(4):72-75.

[13]张义民. 机械振动[M].北京：清华大学出版社，2007.

[14]吕春梅，张义民，冯文周，等. 多跨转子系统频率可靠性灵敏度与稳健设计[J]. 机械工程学报,2012, 48(10):178-183.

LÜChun-mei,ZHANGYi-min,FENGWen-zhou,etal.FrequencyreliabilitysensitivityandrobustdesignoftheMultispanrotorsystem[J].Journalofmechanicalengineering,2012, 48(10):178-183.

[15]曹树谦, 张文德，萧龙翔. 振动结构模态分析-理论、实验与应用[M]. 天津:天津大学出版社，2001.

[16]WUYT.Computationalmethodsforefficientstructurereliabilityandreliabilitysensitivityanalysis[J].AIAAJournal, 1994, 32(8):1717-1723.

第一作者毛杰男，博士生，1987年生

通信作者郝志勇男，博士，教授，博士生导师，1955年生