三参数威布尔分布参数估计及在可靠性分析中的应用
第一作者郑锐男,硕士,工程师,1985年4月生
三参数威布尔分布参数估计及在可靠性分析中的应用
郑锐
(中国船舶重工集团公司第七一六研究所,江苏连云港222006)
摘要:威布尔分布是可靠性中应用最广泛的分布之一。三参数威布尔分布尤其适用于在开始使用时有一时间段内不发生故障的情况。由于该分布的位置参数不等于0,在参数估计时不能采用简单的参数估计方法实现,限制了该分布形式在可靠性分析中的应用。根据三参数威布尔分布的特点提出了一种综合图解法和遗传算法的参数估计方法,应用该方法可以获得更精确的参数估计值。随后应用于某系列数控车床计算机数控系统的故障分析中,验证了参数估计方法的可行性。
关键词:三参数威布尔分布;参数估计;图解法;遗传算法;数控机床
基金项目:国家自然科学
收稿日期:2013-09-03修改稿收到日期:2014-03-27
中图分类号:TG659文献标志码:A
Parameter estimation of three-parameter Weibull distribution and its application in reliability analysis
ZHENGRui(The 716th Research Institute of China Shipbuildnig Industry Corporation, Lianyungang 222006,China)
Abstract:Weibull distribution is one of the most widely used distributions in reliability analysis. However, the application of three-parameter Weibull distribution is often limited due to the fact that its positional parameter is not equal to 0 and its parameters cannot be estimated with simple methods. Actually, the three-parameter Weibull distribution is particularly suitable for the case that there is no fault in a period of time at the beginning of use. Here, a parameter estimation method synthesizing graphical method and genetic algorithm for three-parameter Weibull distribution was presented according to the characteristics of the distribution. Then the three-parameter Weibull distribution with the proposed parameter estimation method was applied in failure analysis of a series of CNC lathes and successful results were achieved.
Key words:three-parameter Weibull distribution; parameter estimation,graphical method; genetic algorithm; CNC machine tools
可靠性分析的首要问题是寻找能够确切反映系统故障机理并与故障数据的分析结果相符合的故障分布规律。常用的方法是将故障数据拟合成某种分布形式,在确定出各分布参数之后,对故障数据进行可靠性评估和预测[1]。
威布尔分布是描述机械系统及其零部件寿命数据分布规律最常用的一种分布形式[2]。两参数威布尔分布凭借其参数估计简单和适应性较强的特点在故障分析中占据重要的地位。两参数威布尔分布描述的设备在t>0的任意时间内都可能发生故障。然而,大量的工程实践证明,许多设备在投入使用后一段时间段内不会发生任何故障,这些设备的故障数据经过威布尔变换后在威布尔概率纸上呈现的不再是一条直线,此时如果仍然采用两参数威布尔分布模型拟合故障数据就可能会给可靠性分析带来较大的误差。三参数威布尔分布尤其适用于这种情况,能够提供更精确的分析结果。
三参数威布尔分布的参数估计相比两参数威布尔分布的参数估计要复杂得多,其最常用的参数估计方法是极大似然法[3]。三参数威布尔分布的似然方程组是非线性的,结构十分复杂,常采用Newtom-Raphson迭代等方法求解。用这种方法求解时,初选值的选择不当会导致迭代过程发散,无法得到最终结果。另外,三参数威布尔分布的参数估计方法还有双线性回归法、概率权重矩法、相关系数优化法、灰色估计法、Bayes统计分析法等[4-8],这些方法针对不同样本容量的适应能力各不相同,但都难免复杂的计算。本文提出一种综合图解法和遗传算法的三参数威布尔分布参数估计方法,其中图解法为遗传算法提供搜索范围,而遗传算法可通过迭代获得更精确的参数估计值。
1参数估计方法
1.1图解法
三参数威布尔分布的可靠度函数表达式为
(1)
式中:β为形状参数,η为尺度参数,γ为位置参数(t<γ时无故障)。
对式(1)两次取自然对数后可以转换为
ln{-ln[R(t)]}=βln(t-γ)-βln(η)
(2)
对式(2)作威布尔变换,即令y=ln{-ln[R(t)]},x=lnt,并不能得到线性函数,但可以利用威布尔概率纸进行参数估计。根据式(2)的性质,当t-γ=0,即x=ln(γ)时,y趋向于-;而当t趋向于时,y=βx-βln(η)。即x=lnγ和y=βx-βln(η)是式(2)经过威布尔变换后的得到的函数的两条渐近线。由此可得三参数威布尔分布参数估计的步骤如下:

(2)在故障数据的WPP图上拟合两条渐近线:其中一条在所有散点左侧,垂直于横坐标,其表达式为x=x0;另一条是当x趋向于∞时的渐近线,其表达式为y=kx-b。根据三参数威布尔分布的图形性质可得以下方程组。
(3)

1.2遗传算法
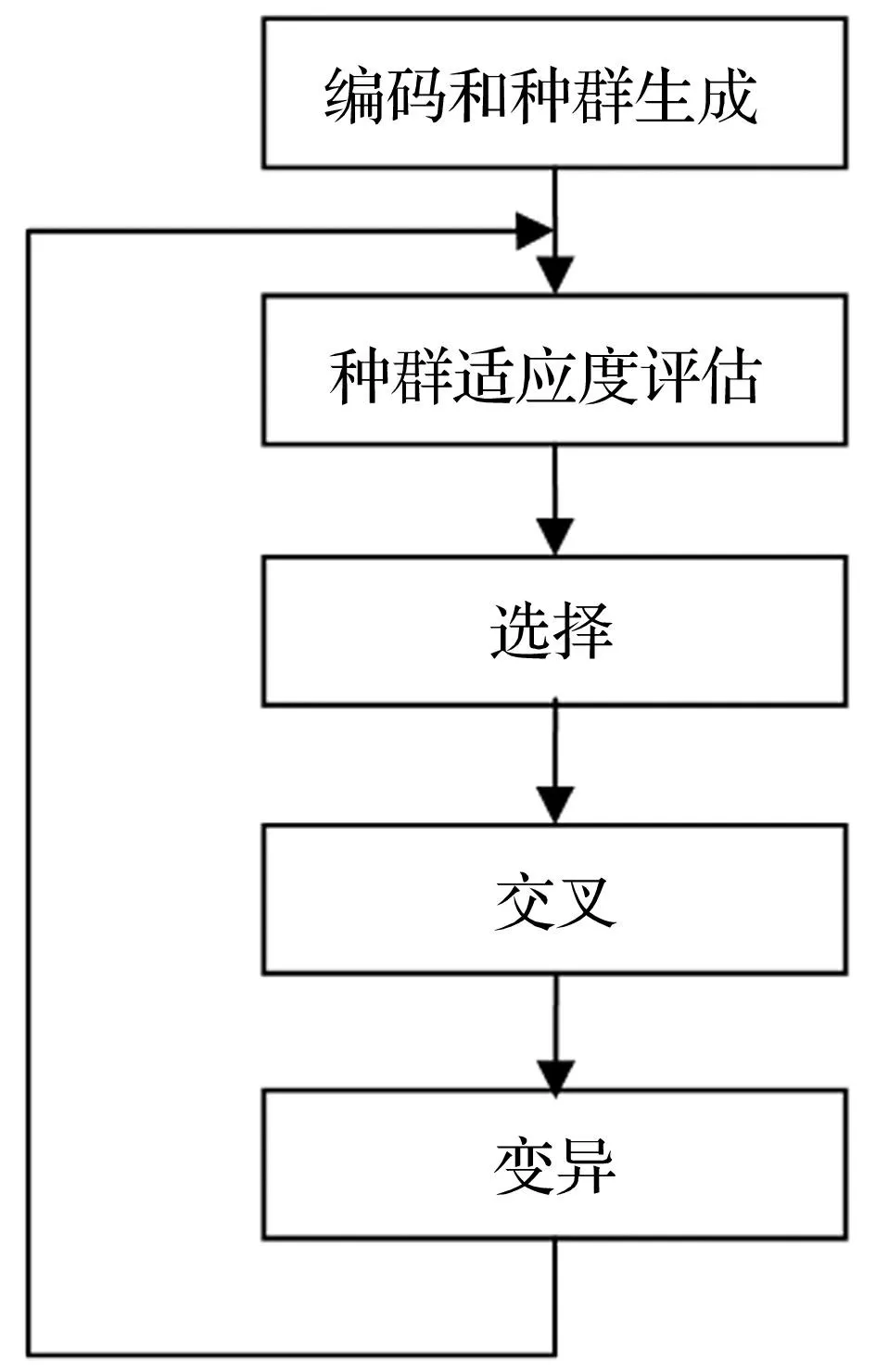
图1 遗传算法流程图 Fig.1Flow Chart of GA
遗传算法(GA)具有较强的全局优化能力,是一种自适应的、智能的搜索技术,其最成功的应用领域是复杂的非线性优化问题。遗传算法是一种群体型操作,该操作以群体中的所有个体为对象,它的基本流程如图1所示,包含6个基本要素。
(1)参数编码。编码是解空间向GA空间的映射,是连接问题与算法的桥梁。编码的方法有二进制编码,实数编码,区间值编码等。编码方法的选择将直接影响选择、杂交、变异等算子的设计,也影响算法的复杂性。
(2)生成初始群体。遗传迭代前,需要首先建立一个由若干初始解(也称为个体)组成的群体,即初始群体。初始群体中的每个个体都是通过随机方法得到的参数编码。
生成初始群体前通常要确定每个参数的范围,称作搜索空间。搜索空间必须足够大,能够涵盖每一个适合的个体,但是太大的搜索空间又会影响收敛的速度,因此搜索空间的定义非常重要。对于三参数威布尔分布的各个参数的搜索空间,这里利用图解法产生的参数估计值获得。首先给定宽松系数θ(0<θ<1),定义分布中每个参数的搜索空间为
(4)
式中:θ值越大,搜索范围越大;反之,越小。
(3)适应度评估。遗传算法在遗传迭代时基本不利用外部信息,仅以适应度函数为依据,利用种群中的每个个体的适应度值进行搜索。适应度值越大的个体被选择的概率越大。因此,适应度函数的选取将直接影响个体的质量,并同样会影响收敛速度。
对于三参数威布尔分布,本文在d检验(柯尔莫哥洛夫-斯米尔诺夫检验,或k-s检验)[9-10]的基础上经过适当的处理作为适应度函数。
d检验法是可靠性分析中常用的检验方法,它比χ2检验法精细,而且还适用于小样本的情况。d检验法是将n个试验数据按由小到大的次序排列,根据假设的分布,计算每个数据对应的R0(ti),将其与经验分布函数Rn(ti)进行比较,其中差值的最大绝对值即检验统计量Dn的观察值。将Dn与临界值Dn,α进行比较。若满足式(5),则接受原假设;否则,拒绝原假设。
(5)
式中:R0(t)为原假设分布函数,即三参数威布尔分布,函数中的参数对应于种群中个体的染色体段。
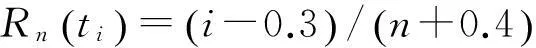

由此可得三参数威布尔分布的适应度函数的表达式如下
Fitness(t)=Dn,α-Dn
(6)
适应度函数的取值越大,表明原假设分布函数越贴近经验分布函数,即获得的分布函数越精确,在遗传迭代中被选择的几率越大。而且这个适应度函数还有一个重要的优势:如果对于某个体使Fitness(t)>0,则可以判定该个体中的参数估计值通过d检验,可以在遗传迭代中直接获得符合d检验的参数估计值。
(4)选择。在对个体适应度进行评价的基础上把优化的个体直接遗传到下一代,或通过配对交叉产生新的个体,再遗传到下一代。
(5)交叉。交叉操作是遗传算法中最主要的操作。交叉的步骤为:首先对种群中个体进行随机配对;然后,在配对个体中随机设定交叉处(一点或多点),配对个体彼此交换部分信息。
(6)变异。变异操作是按位(bit)进行的,即把染色体某一位的内容进行编译。编译操作同样也是随机进行的。一般而言,变异概率都取得较小。变异操作是十分微妙的遗传操作,它需要和交叉操作配合使用,目的是挖掘群体中个体的多样化,克服有可能限于局部解的弊病。
选择、交叉、变异均属遗传算法的基本操作,方法繁多,但仅与收敛速度有关,在此不作赘述,请参看相关文献。
2在可靠性分析中的应用
计算机数控系统(Computer Numerical Control)是数控机床的核心部分,主要有计算机数控装置(CNC)、伺服驱动装置、位置检测装置、可编程控制器PLC和接口电路组成。计算机数控系统的故障往往会带来较大的危害度,其可靠性对于数控机床至关重要。表1给出了某系列数控机床数控系统出厂使用半年的故障数据。
图2 给出了数控机床计算机数控系统故障间隔时间的散点图,从图中可以看出散点并不呈一条直线,具有明显的拐点,符合三参数威布尔分布的特征。故而假设计算机数控系统的故障间隔时间服从三参数威布尔分布。按照图解法的步骤,在WPP图上作两条渐进线L1和L2,见图2。两条渐近线表达式分别为:
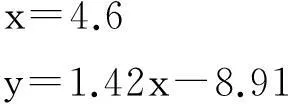
(7)

图2 计算机数控系统故障数据WPP及渐近线图 Fig.2 WPP and asymptotic line graph of CNC system

序号tiRn(ti)xiyi11040.96734.6444-3.403521220.92064.8040-2.49173171———41710.82715.1417-1.661652570.78045.5491-1.394462730.73365.6095-1.17217282———82820.64025.6419-0.807493070.59355.7268-0.6505103740.54675.9243-0.5045113860.50005.9558-0.3665124940.45336.2025-0.2341135010.40656.2166-0.1053145150.35986.24420.0219155760.31316.35610.1495166740.26646.51320.2798176990.21966.54970.4160187010.17296.55250.5625198030.12626.68840.72762010360.07946.94310.92932111980.03277.08841.2297
由此可得三参数威布尔分布图解法的初始解为:β=1.42,η=530.94,γ=99.48。
令宽松系数θ=0.5,可得三参数威布尔分布的搜索空间为

(8)
运用遗传算法进行遗传迭代可得三参数威布尔分布的参数估计值及适应度见表2,其适应度大于0且远大于图解法得到的适应度,说明遗传算法的参数估计值不但能通过d检验,而且计算精度远大于图解法。

表2 参数的估计值及其适应度
因此,计算机数控系统的故障间隔时间服从三参数威布尔分布的假设成立,其可靠度函数为
(9)
图3给出了计算机数控系统的可靠性函数曲线,图中的散点即为故障时间点的经验分布函数值。图中的散点均匀的分布在曲线的两侧,说明三参数威布尔分布及文中给出参数估计方法对于计算机数控系统的故障分析是适用的。

图3 计算机数控系统的可靠度函数图 Fig.3 Reliability graph of CNC system
3结论
首先揭示了三参数威布尔分布在可靠性分析中的特殊意义,然后针对其参数估计复杂的问题,提出了一种综合图解法和遗传算法的参数估计方法。该方法以图解法的解为基础形成搜索空间,用遗传算法提高解的精度,从而得到更精确的参数估计值。随后三参数威布尔分布应用于计算机数控系统的可靠性分析中,验证了本文提出的参数估计方法的可行性。本文提出的参数估计方法对于其他复杂的威布尔分布形式(例如竞争威布尔分布)的参数估计具有一定的启示意义。
参考文献
[1]张英芝,申桂香,吴甦,等. 随机结尾数控机床三参数威布尔分布模型[J]. 吉林大学学报(工学版),2009,39(2):378-381.
ZHANG Ying-zhi, SHEN Gui-xiang, WU Su, et al. 3-parameter Weibull distribution for random truncated NC machine tool falt data[J]. Journal of Jilin University (Engineering and Technology Edition), 2009,39(2):378-381.
[2]Murthy D N P, Xie M, et al. Weibull models [M]. New York ,John Wiley,2004.
[3]杨谋存,聂宏. 三参数Weibull分布参数的极大似然估计数值解法[J]. 南京航空航天大学学报, 2007,39(1):22-25.
YANG Mou-cun, NIE Hong. Advanced algorithm for maximum likelihood estimation of three parameter weibull distribution[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007,39(1):22-25.
[4]严晓东,马翔,郑荣跃. 三参数威布尔分布参数估计方法比较[J]. 宁波大学学报(理工版),2005,18(3):301-305.
YAN Xiao-dong, MA Xiang, ZHENG Rong-yue. Comparion of the parameters estimation methods for 3-parameter weibull distribution[J].Journal of Ningbo University (NSEE), 2005,18(3):301-305.
[5]Tsionas E G. Posterior analysis, prediction and reliability in three-parameter Weibull distributions [C]. Communications in Statistic-Theory and Methods, 2000,29(7):1435-1449.
[6]杨志忠,刘瑞元. 三参数Weibull分布参数估计求法改进[J]. 工程数学学报, 2004,21(2):281-284.
YANG Zhi-zhong, LIU Rui-yuan. Improvement of parameter estimation method for Three-parameter Weibull distribution[J]. Journal of Engineering Mathematics,2004,21(2):281-284.
[7]Teimouri M, Gupta A K. On the Three-parameter weibull distribution shape parameter estimaion[J]. Journal of Data Science,2013,11:403-414.
[8]卢安平,赵林,郭增伟,等.基于Monte Carlo法的极值分布类型及其参数估计方法比较[J]. 哈尔滨工业大学学报, 2013,45(2):87-95.
LU An-ping, ZHAO Lin, GUO Zeng-wei, et al. A comparative study of extreme value distribution and parameterestimation based on the Monte Carlo method[J]. Journal of Harbin Institute of Technology, 2013,45(2):87-95.
[9]陆阳,王强, 岳峰, 等.软件可靠性关键参数判定的据估计方法[J]. 系统工程理论与实践,2014,34(1): 248-254.
LU Yang,WANG Qiang, YUE Feng, et al. Key parameter judgment with moment estimation in software reliability prediction[J].Systems Engneering-Theory & Practice,2014,34(1): 248-254.
[10]Xing L, Boddu P, Sun Y, et al. Reliability analysis of static and dynamic fault-tolerant systems subject to probabilistic common-cause failures [J]. Proceedings of the Institution of Mechanical Engineers part 0-Journal of Risk and Reliability,2010,224(1):43-45.


