阻尼矩阵选取对核电厂结构地震响应的影响分析

阻尼矩阵选取对核电厂结构地震响应的影响分析

李小军1,3,侯春林2,潘蓉2,周国良2,杨宇2

(1. 北京工业大学建筑工程学院，北京100124； 2.国家环保总局核与辐射安全中心，北京100082；3.中国地震局地球物理研究所，北京100080)

摘要：已有研究表明时程动力法中阻尼矩阵的确定对复杂结构工程的地震响应有明显的影响，而核电厂安全相关结构在抗震分析时通常采用时程动力法。为研究阻尼矩阵的选取对核电厂结构的地震响应的影响，从比例阻尼拟合的精度出发，基于结构不同振型对结构产生的影响程度入手，建立更为精确的结构阻尼模型，即等效比例阻尼，并进一步考虑结构自振特性以加权最小二乘法拟合确定等效比例阻尼系数，提出了核电厂结构地震响应分析相应的计算方法。计算结果表明，该方法较传统比例阻尼的方法更接近精确解，是核电工程抗震分析的一个实用参考应用。

关键词：核电厂；抗震分析；阻尼模型；时程动力法

中图分类号:P315文献标志码：A

基金项目：国家科技支撑计划(2013BAJ08B03)；国家自然科学基金(50978218，51108376)；教育部高等学校博士学科点专项科研基金(20136120110003)；陕西省科研项目(2012K12-03-01，2011KTCQ03-05，2013JC16)

收稿日期：2013-08-26修改稿收到日期：2014-01-02

Effectofdampingmatrixselectiononseismicresponseofnuclearpowerplantstructures

LI Xiao-jun1,3, HOU Chun-lin2,PANRong2,ZHOUGuo-liang2,YANGYu2(1.TheCollegeofArchitectureandCivilEngineering,BeijingUniversityofTechnology,Beijing100124,China；2.NuclearandRadiationSafetyCentre,MinistryofEnvironmentalProtectionofthePeople’sRepublicofChina,Beijing100082,China；3.InstituteofGeophysics,ChinaEarthquakeAdministration,Beijing100081,China)

Abstract:To study the effect of determination of damping matrix on the seismic response of nuclear power plant structures, fitting accuracy of the proportional damping of nuclear power plant structures and the influence of different shape of structures were considered. On this basis, a more precise model, that is, an equivalent proportional damping model was set up. Furthermore, a corresponding method for the seismic response analysis of nuclear power plant structures was proposed based on determining the proportional damping coefficient by weighted least square fitting method. The application and analysis show that the results by the proposed method are closer to the exact solutions than by the method with traditional damping coefficient, and it is suitable for the seismic response of nuclear power plant structures.

Keywords:nuclearpowerplant;seismicanalysis;dampingmodel;time-historymethod

工程结构动力反应过程中存在能量的耗散，并导致外部能量输入结束后结构由振动状态逐步衰减到静止状态。这种由于阻尼而消耗的能量被称之为阻尼耗能，阻尼用来描述结构振动过程中某种能量耗散的方式，结构动力分析中阻尼被视为结构与支撑之间的摩擦、材料之间的内摩擦、周围介质的阻力等引起的振动衰减作用[1]。阻尼是结构抗震分析中一个重要因素，在结构的振动分析中，各种响应函数都包括阻尼这个参数，能否正确设定阻尼，直接影响到结构动力分析结果的可靠性。阻尼选取不恰当时，其阻尼值一个较小的差异可能会导致结构响应上成倍的变化[2,9,14-15]。由于阻尼的本质和表象的复杂性，提出的模型众多[11-13]，阻尼矩阵的选取也各不相同。针对结构动力时程分析，经过近几十年的研究，已经提出了多种阻尼表达方式[10]，其中以粘性比例阻尼最为常用，其中最具代表性的有Rayleigh阻尼模型、Cauchy阻尼模型、Clough阻尼模型等。其它比例阻尼模型多是Rayleigh阻尼模型的拓展形式，Rayleigh阻尼模型由于物理关系明确，且Rayleigh阻尼矩阵可通过模态向量正交化为对角矩阵，便于动力方程解耦和显式计算而得到了广泛应用。但Rayleigh阻尼矩阵建立方式也不尽相同，有关文献讨论了Rayleigh阻尼矩阵的不同建立方式对大跨桥梁、土石坝等结构动力反应的影响，研究显示不同阻尼矩阵对计算结果有较大的影响。在核电厂结构抗震分析计算过程中，阻尼矩阵的选取是否合理同样会影响核电厂结构和设备抗震分析结果，阻尼矩阵的合理选取成为核电厂抗震设防中值得关注的重要问题。要研究阻尼矩阵选取对核电厂结构地震反应的影响，应首先搞清楚核电厂结构地震反应的分析方法。对于安全相关的核电厂结构抗震分析计算，中国《核电厂抗震设计规范》(GB50267-97)[1]规定Ⅰ、Ⅱ类物项的抗震设计可采用等效静力计算法、反应谱法和时程动力分析法。美国土木工程协会《核电厂结构和安全相关构件的抗震分析》(ASCE4-98)[2]和《标准审查大纲》(NUREG-0800 3.7.2)[3]推荐在核电厂结构响应分析时，可采用时程法、反应谱法、复频响应分析法和等效静力法。实际工程经验中，常使用时程动力法计算核电厂结构的地震反应，以便给出设备的抗震输入。时程动力法分模态叠加时程动力法和逐步积分时程动力法，逐步积分动力时程法要应用到Rayleigh阻尼矩阵，因此需研究阻尼矩阵选取方法对核电厂结构地震反应的影响。参考已有研究，模态叠加时程法的计算结果可作为研究阻尼矩阵选取对核电厂结构地震反应影响的参考，本文则基于国内三代机组CAP1400的核岛结构模型[4]，以模态叠加法动力时程分析结果为参考，研究不同阻尼对核电厂结构地震反应的影响。

1核电厂结构动力时程分析方法及阻尼矩阵的选取

1.1核电厂结构动力时程分析方法

核电厂抗震分析中，常常建立精细的结构动力有限元模型，采用动力时程分析法计算结构的地震反应。在线弹性条件下，核电厂结构体系的地震反应分析动力方程为：

(1)

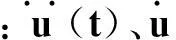
对于核电厂结构时程动力分析，可选用模态叠加法或逐步积分法进行求解。模态叠加法时程分析是将一个多自由度体系振动分解成不同振型的单自由度体系的振动来求解，单自由度系统的动力响应分析可使用杜哈美精确积分。它要求输入各振型的阻尼比。这种方法具有运算速度快，阻尼输入准确等优点。但目前模态叠加时程分析方法仅适用于线弹性状态下结构时程动力分析，不适合结构的非线性计算。另一类方法是逐步积分时程动力分析方法，采用这类方法可进行结构弹塑性时程动力分析。其积分方法又可分成常加速度法、线性加速度法、Wilson、Newmarkα-β方法等。使用模态叠加动力时程分析时，结构阻尼比类型选择模态阻尼比。此时，应根据结构物的结构特征及相关的法规规定确定动力分析中的模态阻尼比，规范中规定的各种结构形式的阻尼比即为模态阻尼比。当在动力计算中必须考虑非线性因素时，则只能采用直接积分法进行动力分析，需采用比例阻尼建立合理的阻尼矩阵。

1.2核电厂结构动力时程分析时阻尼矩阵的选取

本文基于ANSYS软件开展核电厂结构抗震分析中阻尼矩阵的实现及选取方法的研究。在结构分析中，可使用多种阻尼输入，按不同的命令可分为：ALPHD输入α阻尼参数；BETAD输入β阻尼参数；DMPRAT：输入整个结构的阻尼比ζ；MDAMP输入与各振型频率对应的模态阻尼比；DAMP输入对应于某种材料的材料阻尼系数；与以上几种命令的输入对应的ANSYS计算的总阻尼阵C分别为：

(2)

式中：M是结构中有阻尼的材料种类数，n是具有特有阻尼的单元类型数。前两项是用α与β定义的Rayleigh阻尼，第三项是与整体结构的阻尼比ζ对应的阻尼阵，第四项是材料阻尼，最后一项是一些单元特有的单元阻尼阵。在各种阻尼输入下，程序计算出的第i 阶模态的总模态阻尼比可表示为：

(3)

式中，前两项是α阻尼与β阻尼对应的模态阻尼比，第三项是输入的整个结构的阻尼比，第四项是输入的模态阻尼比，最后一项是m种材料的材料阻尼系数ξ产生的模态阻尼比。

(4)

式中：Ej是第j种材料对应的模态应变能。

当采用模态叠加法进行时程动力分析时，ANSYS对材料阻尼与结构阻尼比直接使用；当采用逐步积分时程动力分析时，最常用也是比较简单的阻尼是Rayleigh阻尼，核电厂实际工程经验中也亦常选取Rayleigh阻尼。值得一提的是，在逐步积分过程中可同时使用材料阻尼和Rayleigh阻尼，但计算结果较模态叠加法小很多，尽管整个计算过程阻尼阵可以建立，但计算结果是不准确的，从式(5)求α与β阻尼系数过程即可以得到验证，因此，在逐步积分时程动力分析中，仅可以使用Rayleigh阻尼。实际计算过程中，ANSYS里分别用ALPHD与BETAD命令输入α与β阻尼系数以实现Rayleigh阻尼阻尼矩阵的建立。在实际工程计算时，已知结构总阻尼比是ζ，使选用的两个频率点上α阻尼与β阻尼产生的等效阻尼比与其相等，就可以求出相应的α与β阻尼系数，计算过程如下：

(5)

可计算得到：

(6)

式中， ω1和ω2为无阻尼的自振频率。对于自振频率的定义范围，一般是应与导致结构反应的频率范围相一致，这需要考虑自振频率特性和输入地震波的频谱特性。

实际工程经验中，结构相对简单的模型建立阻尼矩阵时可选取振型参与系数最大的两阶振型，即ω1和ω2结构的前两阶频率；或者当考虑结构自振频率特性和输入地震波的频谱特性时，选取感兴趣的两阶频率，即ω1和ω2为与结构反应一致的频率段。这两种方法均是基于两阶阵型频率建立结构体的阻尼矩阵。对于刚度均匀的体系，一般取相应振动的两阶频率常可取得合理的结果，对复杂结构体系则需要进一步研究阻尼矩阵对结构体系的影响。已有的研究结果表明阻尼矩阵选取方法不同会对土石坝反应[6]、大跨桥梁[7,14]及超高层结构[7,15]等不同类型结构产生不同程度的地震反应影响。为此，本文开展了不同阻尼矩阵选取对核电厂结构地震响应的影响，并基于已有的阻尼类型提出了一种新的阻尼矩阵的选取方法。

1.3建议的阻尼矩阵确定方法

已有研究表明，各种粘滞阻尼模型的实质都是对结构的各个振型阻尼比的一种拟合[8]，也就是说并不是从物理概念出发，而是从数学处理方法的角度出发，只不过是拟合函数各不相同[9]。基于此，本文提出一个考虑结构自振特性的阻尼矩阵建立方法，并和传统的阻尼矩阵计算方法进行比较。本文的阻尼实际选取过程如下：对于感兴趣的振型频率ω1,ω2,...,ωn，按其重要性赋给权重为w1,w2,...,wn。通常情况下，频率越低，这个振型的阻尼设定越重要，因而权重应该按照频率大小单调递减。推荐的权重函数是w=1/ω,或者w=exp(-ω)。根据上述参数，Rayleigh阻尼参数α,β 的拟合方法为求解如下最小化的优化问题，即：

(7)

此目标函数为关于α,β 的凸函数，可以看成加权最小二乘拟合。对于这两种权重，仍需验证哪一种在实际工程计算中更适用。

2计算分析模型及相关参数

2.1结构模型

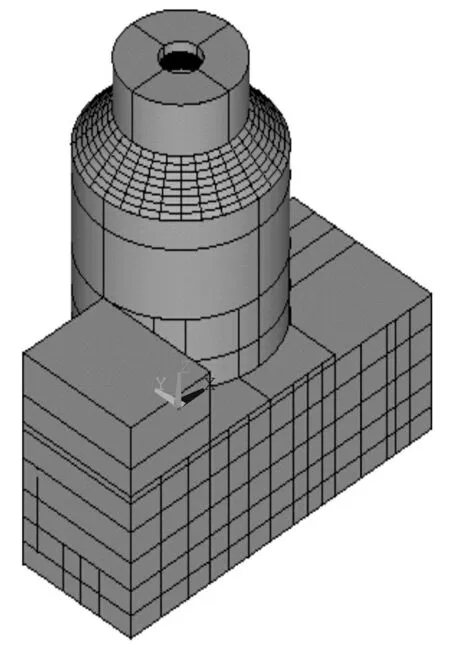
图1　CAP1400机组屏蔽厂房结构 Fig.1 CAP1400 Nuclear Island structures

为分析阻尼矩阵选取方法对核电厂结构地震响应的影响，本文选取CAP1400屏蔽厂房模型，CAP1400核岛结构模型包括安全壳厂房(钢安全壳和安全壳内部结构)、屏蔽厂房(屏蔽厂房和辅助厂房)，这些结构坐落在同一个基础上。对核岛厂房建立三维有限元模型，依据整体电厂的布置，可分为：一个耦合的屏蔽厂房和辅助厂房的有限元模型(简称ASB)，一个安全壳内部结构的有限元模型(简称CIS)，一个屏蔽厂房屋顶的有限元模型和一个钢安全壳的轴对称板壳模型(简称ASB)。在CAP1400实际设计分析过程中，这些厂房单独建模，然后耦合在一起进行抗震分析，而对于底部固定处理的情况下，屏蔽厂房和辅助厂房的有限元模型在抗震分析是可以解耦的，即可以单独进行抗震分析。本文为分析阻尼矩阵对核电厂结构地震响应的影响，可只选取CAP1400核电厂屏蔽厂房和辅助厂房结构模型，简称为CAP1400屏蔽厂房模型。CAP1400屏蔽厂房模型包括屏蔽厂房和辅助厂房以及安全壳内部结构的钢筋混凝土部分，其有限元模型基于混凝土全截面建立，指定结构墙体和楼板混凝土抗压强度对应的弹性模量，采用调整结构单元材料密度的方法来考虑混凝土的重度加上均匀分布的等效荷载。采用等效附加2.5kN/m2的楼面活荷载或75%的屋面雪荷载来考虑诸如小设备、管道和电缆管的分布荷载。辅助厂房和屏蔽厂房以板壳单元进行模拟，有限元模型底部在基础底板的中间，标高为-11.700m。安全壳的内部结构的底部用实体单元模拟，在此有限元模型中，为方便有限元模型的底端约束，内部结构的实体单元有限元模型底部也取为-11.700m，内部结构实体与屏蔽厂房壳体之间采用多点约束技术连接。辅助厂房和屏蔽厂房模型与安全壳模型间的交界面半径为23.435m，在屏蔽厂房的中间面。CAP1400屏蔽厂房的有限元模型如图1所示；CAP1400屏蔽厂房屋顶结构钢梁有限元模型如图2所示。

图2　CAP1400屋顶钢梁模型 Fig.2 Stick Model of CAP1400 Nuclear Island structures

与以往核电厂(M310、CPR1000等)抗震分析方法不同的是，CAP1400选用的是模态叠加法时程法分析，得到抗震系统的分析和设计所需的构筑物反应。故本文选取CAP1400核岛结构模型，一方面可复核CAP1400设计过程中核岛结构的抗震分析计算结果，另一方面可参考已有CAP1400核电厂结构的模态叠加法抗震分析计算结果，研究阻尼矩阵选取对核电厂结构地震响应的影响。CAP1400核电厂结构模型底端固定时，前几阶主要模态分析计算结果如表1所示。耦合的屏蔽厂房和辅助厂房的模型中屏蔽厂房壳单元质量为112 368.6t，梁单元542.3t，质量单元3 268.9t，共计116 179.8t。加上内部结构底座实体单元的质量，与CAP1400提交报告中ASB模型的主要模态振型及总质量128 400t提供的结果基本一致。

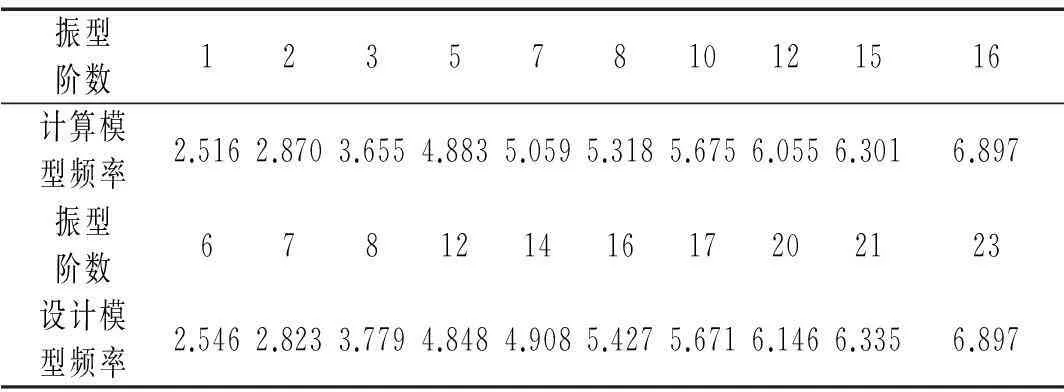
表1　 CAP1400屏蔽厂房结构模态频率的

2.2地震动时程

为保证与CAP1400核电厂原有设计文件中计算结果的一致性，拟选择与核电厂要求的抗震设计强度匹配的输入地震动。本节基于CAP1400核电厂标准设计反应谱拟合了一组人工时程，该组时程包括水平向x，y方向和竖直z三个方向上的三条人工时程。每条人工时程的地震动峰值加速度以0.30g标定、时程间隔为0.01s、总持时为30s；人工时程能满足能同时包络5个阻尼比(2%、3%、4%、5%、7%)下的设计反应谱的要求、《核电厂抗震设计规范》和NUREG-0800中3.7.1节对人工时程的相关规定，包括拟合人工时程所选频率控制点，拟合精度和功率谱密度要求等。该组人工时程三个方向的统计相关性系数分别为0.085、0.008和0.130，均小于0.16，满足单组人工时程三个方向相互独立的要求。人工地震动时程如图3所示，分别为水平向x，y方向和竖直z三个方向的三条时程。

图3　计算输入地震动加速度时程 Fig.3 Acceleration time-history of the input ground motion

3计算结果比较

3.1不同方法拟合的阻尼系数

为分析不同阻尼矩阵对核电厂结构地震反应的影响，本节所列的图表中将模态叠加法动力时程分析计算结果标注为模态法，阻尼系数计算取前两阶振型频率时2.516-2.870Hz时标注为方法一，阻尼系数计算取与结构相关的频率段即2.516-33Hz时标注为方法二，阻尼系数计算取整个频率段0.4-33Hz时标注为方法三，阻尼系数计算取本文推荐的最小二乘法计算时，权重函数为w=1/ω时标注为方法四，权重函数为w=exp(-ω)时标注为方法五。不同阻尼矩阵选取计算得到的α与β值如表2所示，依据式(3)得到实际计算过程中不同阻尼矩阵选取使用的阻尼如图4所示。由表2和图4可知，不同阻尼矩阵选取所建立的计算阻尼矩阵是有一定差异，这种差异对核电厂结构地震反应造成的影响需进一步分析。

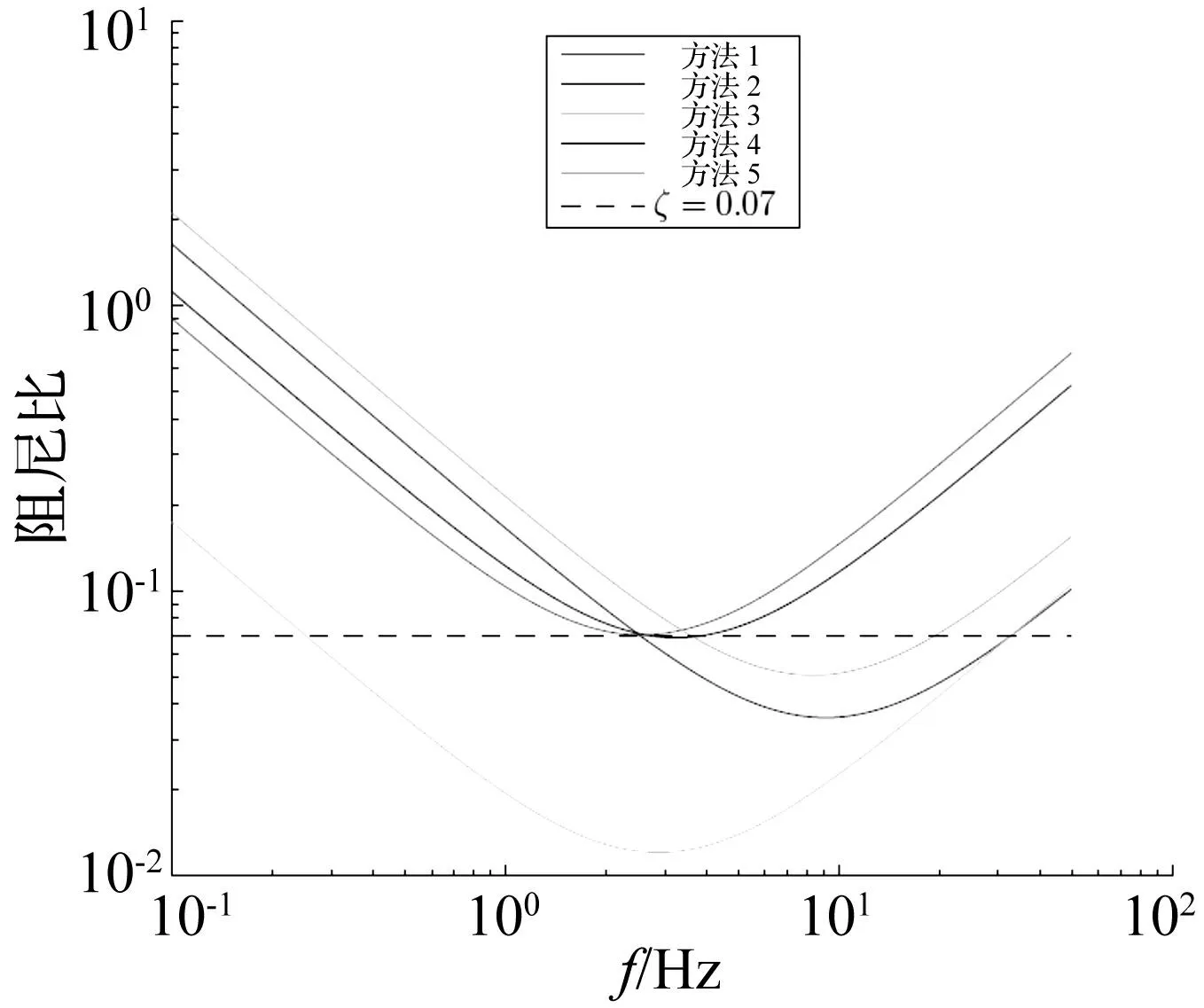
图4　不同的阻尼矩阵方法对应的阻尼值随频率的变化 Fig.4 Variation of the damping ratios related to different methods of damping matrix with frequency

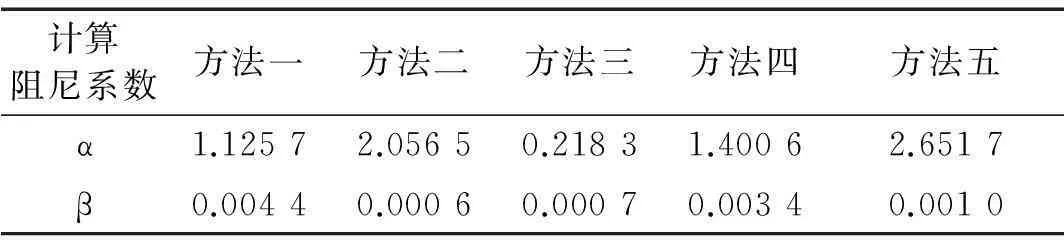
计算阻尼系数方法一方法二方法三方法四方法五α1.12572.05650.21831.40062.6517β0.00440.00060.00070.00340.0010

3.2不同阻尼矩阵选取的计算结果

为保证计算结果的正确性及可靠性，选取计算结果比较点为屏蔽厂房与辅助厂房的节点7 320(低于辅

助厂房屋顶的某一标高)、节点6 866(辅助厂房屋顶处的标高)、节点1 658(进气口下方某一标高)、节点1 500(进气口上方某一标高)、节点3 460(屏蔽厂房上部水箱的底部标高)和节点3316(屏蔽厂房上部水箱的顶部标高)。采用不同阻尼矩阵计算对应的节点峰值加速度比较如表3所示，对应的节点最大相对位移比较如表4所示，对应的节点5%阻尼反应谱的比较如图5所示。

由表3可知，方法一、方法二和方法三中，同一节点同一方向的峰值加速度值均有差异，方法二和方法三与模态法计算结果差异较大，方法二和方法三的计算结果过于保守，尤其是方法三，偏离实际结果最大，方法一的计算结果与模态法较接近，但对于7 320节点的x向峰值加速度仍有19.7%的差异；方法四和方法五中，方法五计算结果偏大，方法四与模态法计算果相近，方法五的计算结果同方法二和方法三一样，计算结果过于保守；方法四和方法一中，对于7 320节点的x向峰值加速度，方法四与模态法的计算结果的差异可降低至12.4%；对于有些节点，如1 500节点的x向峰值加速度，方法四与模态法计算结果一样。由以上分析可知，计算同一节点峰值加速度时，方法四更接近模态法的计算结果。

表3　采用的阻尼矩阵方法时观测节点的峰值加速度计算值(单位： g)

表4　采用不同的阻尼矩阵方法时观测节点的峰值加速度计算值(单位： g)

图5　采用不同的阻尼矩阵方法时观测节点的加速度反应谱计算值比较 Fig.5 Comparison of the computed spectral accelerations of observation nodes related to different methods of damping matrix

由表4可知，方法一、方法二和方法三中，同一节点同一方向的最大相对位移值均有差异，方法三与模态法计算结果差异最大，计算结果过于保守，方法一的计算结果与模态法较接近，如对于7 320节点的x向最大相对位移值有4.1%的差异；方法四和方法五中，方法五计算结果偏大，方法四与模态法计算结果较接近；方法四和方法一中，对于7 320节点的x向峰值加速度，方法四与模态法的计算结果的差异降低至1.8%，几乎一样；对于有些节点，如1 500节点的x向最大相对位移，方法一和方法四与模态法计算结果差异均在小数点后的第五位有效数字。由以上分析可知，计算同一节点最大相对位移时，方法一和方法四两种计算方法与模态法计算结果均比较一致，差异都在5%范围已内，但两种方法相比较，方法四的计算结果较方法一更为精确些。

由图5可知，采用不同的阻尼矩阵方法的同一节点相同方向的加速度反应谱均有差异，方法二、方法三和方法五的计算结果均大于模态法，且方法三的计算结果与模态法差异最大，方法一和方法四的计算结果均小于模态法，但方法四的计算结果较方法一更接近于模态法的精确解。

综上所述，由阻尼矩阵选取方法的不同计算得到的节点峰值加速度、最大相对位移和5%阻尼的加速度反应谱的比较可知，本文提出的权重函数w=1/ω的最小二乘法计算的阻尼矩阵建立方法与模态法计算的精确解更为接近。

4结论

已有研究表明，复杂结构工程进行动力时程分析中，结构阻尼对计算结果影响非常大，而由于结构阻尼形成机理的复杂性，研究结果差异性较大。本文基于CAP1400三代核电机组的屏蔽厂房结构，选用传统的阻尼矩阵的建立方法及本文提出的两种拟合比例阻尼的新方法，以模态法时程动力分析结果为参考精确解，量化了阻尼矩阵的选取对核电厂结构地震反应的峰值加速度、相对最大位移及加速度反应谱之间的差异，得到以下认识：

(1)在核电厂抗震分析时，线性状态下推荐使用模态叠加法时程动力分析法，该方法可考虑结构的不同结构材料阻尼，计算结果较逐步积分时程动力分析结构保守准确；

(2)当使用逐步积分时程动力分析法进行核电厂抗震分析时，依据一定频率段建立阻尼的计算结果过于保守，依据前两阶阵型频率建立阻尼矩阵的方法优于依据一定频率段建立阻尼的计算结果，但依据前两阶阵型频率建立阻尼矩阵的计算结果与精确解仍有一定的差异，偏不保守，需进一步改进；

(3)本文提出的考虑结构自振特性的以w=1/ω为权重函数的最小二乘法拟合阻尼系数的方法较传统方法的分析结果更接近精确解，可供核电厂实际结构工程线性抗震分析时使用，同时也可在核电厂结构进行非线性分析时如抗震裕量评估(SMA)及考虑地基-结构相互作用分析过程时应用参考。

参考文献

[1]中华人民共和国国家标准。核电厂抗震设计规范，GB/50267-97[S].1997.

[2]AmericanSocietyofCivilEngineers.SeismicAnalysisofSafety-RelatedNuclearStructuresandCommentary,ASCE4-98Standard[S]. 2000.

[3]U.S.NuclearRegulatoryCommission.StandardReviewPlan,NUREG-0800,Revison3[S]. 2007.

[4]国家核电上海核工程研究设计院.CAP1400初步安全分析报告第三章构筑物、部件、设备和系统的设计[R]. 上海：2012.

[5]邹德高，徐斌，孔宪京. 瑞利阻尼系数确定方法对高土石坝地震反应的影响研究[J].岩土力学, 2011, 32(3): 797-803.

ZOUDe-gao,XUBin,KONGXian-jin，StudyofinfluenceofdifferentmethodsforcalculatingRayleighdampingcoefficientonhignearth-rockdamseismicresponse[J].RockandSoilMechanics, 2011, 32(3): 797-803.

[6]张静.大型结构地震反应分析中阻尼矩阵的计算模型[D].上海：同济大学土木工程学院，2009.

[7]杨志勇，李桂青，瞿伟廉. 结构阻尼的发展及其研究近况[J]，武汉工业大学学报，2000，22(3):38-41.

YANGZhi-yong,LIGui-qing,ZHAIWei-lian.Theresearchhistoryandrecentdevelepmentofstructuraldamping[J].JournalofWuhanUniversityofTechnology,2000，22(3):38-41.

[8]黄宗明，白绍良，赖明. 结构地震反应时程分析中的阻尼问题评述[J].地震工程与工程振动.1996，16(2)：95-102.

HUANGZong-ming，BAIShao-liang，LAIMing.Reviewonthedampinginearthquakeresponsetime-historyanalysisofstructures[J].EarthquakeEngineeringandEngineeringVibration,1996,16(2):95-102.

[9]淡丹辉，孙利民. 结构动力有限元分析的阻尼建模及评价[J].振动与冲击，2007, 26(2)：121-124.

DANDan-hui，SUNLi-min.Dampingmodelingandevaluationofstructuraldynamicfiniteelementanalysis[J].JournalofVibrationandShock，2007, 26(2)：121-124.

[10]黄宗明. 结构地震反应时程分析中的阻尼研究[D].重庆：重庆建筑大学，1995.

[11]董军，邓洪州，王肇民. 结构动力分析阻尼模型研究[J].世界地震工程，2000，16(4): 63-69.

DONGJun,DENGHong-zhou,WANGZhao-min.Studiesonthedampingmodelsforstructuraldynamictimehistoryanalysis[J].WorldInformationonEarthquakeEngineering,2000,16(4):63-69.

[12]李田. 结构时程动力分析中的阻尼取值研究[J].土木工程学报,1997,30(3):68-73.

LITian.Astudyondampingvaluesappliedtothetime-historydynamicanalysisofstructures[J].ChinaCivilEngineeringSociety,1997,30(3):68-73.

[13]楼梦麟，张静.大跨度拱桥地震反应分析中阻尼模型的讨论[J]. 振动与冲击，2009，(5)：22-26.

LOUMeng-lin，ZHANGJing.Discussionondampingmodelsforseismicresponseanalysisoflong-spanbridge[J].JournalofVibrationandShock, 2009，(5)：22-26.

[14]楼梦麟，隋磊，沈飞. 不同阻尼矩阵建模对超高层结构地震反应分析的影响[J].结构工程师，2013, 29(1):55-61.

LOUMeng-lin,SUILei,SHENFei.Effectsofdampingmatrixmodelingonseismicresponseofsuperhigh-risestructures[J].StructuralEngineers,2013, 29(1):55-61.

第一作者郑山锁男，博士后，教授，博士生导师，1960年4月生