脉冲风洞测力系统建模与载荷辨识方法研究

脉冲风洞测力系统建模与载荷辨识方法研究

王锋1,2，贺伟1，毛鹏飞1，张小庆1

(1.中国空气动力研究与发展中心吸气式高超声速技术研究中心，绵阳6210002.中国空气动力研究与发展中心高超声速冲压发动机技术重点实验室，绵阳621000)

摘要：将载荷辨识技术应用于脉冲燃烧风洞模型测力。用子结构综合法建立了测力试验系统的动力学模型，在时域内将动力学方程进行离散，建立起天平测量信号与模型气动载荷历程之间的线性关系，作为载荷辨识的模型。采用Tikhonov正则化和子空间投影法相结合的混合正则化方法，将高维的、不适定的载荷辨识问题转化为低维的适定问题，以利于快速求解。提出了一种新方法来确定合适的投影子空间维数，然后应用L曲线准则来寻找低维正则化问题的最优正则化参数。最后通过算例验证了系统建模方法的精度和载荷辨识算法的有效性与稳定性。

关键词：脉冲风洞;动力学建模;载荷辨识;正则化;反问题

中图分类号:V231;O32文献标志码：A

Dynamicmodelingoftestingsysteminimpulsefacilitiesandloadidentificationmethod

WANG Feng1,2, HE Wei1,MAOPeng-fei1,ZHANGXiao-qing1(1.Air-breathingHypersonicTechnologyResearchCenter,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China;2.ScienceandTechnologyonScramjetLaboratory,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China)

Abstract:Load identification method was applied to force measurement in impulse combustion facilities. The dynamic model of the testing system was built using substructure synthesis method. Then, the differential equations were discretized to establish the linear relationship between the outputs of balance and the dynamic forces history acting on the aircraft model. A hybrid regularization method which combines the Tikhonov regularization and subspace projection method was proposed to solve the load identification problem. The hybrid method converts the ill-conditioned large scale problem into a well-posed small scale problem which can be solved easily. A new method was proposed to determine the size of the projection subspace. The L-curve criteria was employed to search the optimal regularization parameter of the dimension-reduced problem. The accuracy of the structural dynamic modeling method and the effective and stability of the load identification method were validated by a numerical example.

Keywords:impulsefacilities;structuraldynamicmodeling;loadidentification;regularization;inverseproblem

吸气式高超声速飞行器是当前国际航空航天技术的热点研究领域，地面风洞试验是最重要的研究手段，脉冲燃烧风洞是国内目前开展大尺度超燃发动机和机体-推进一体化高超声速飞行器试验研究的主力设备之一，具有口径大、建造和运行成本较低的优点。由于其有效的试验时间较短，只有约200ms～300ms，给模型测力试验带来一定的困难。目前采用常规的测力方法，为了在短时间内测得模型的气动力，需尽量降低模型的质量，同时尽量提高天平的刚度，以便提高试验系统的响应速度。吸气式飞行器采用机身和推进系统一体化设计，内外流紧密耦合，为了反映真实的气动-推进特性，希望采用全尺寸或接近全尺寸的试验模型。所以，目前在风洞开展试验的飞行器模型尺寸和质量越来越大，导致试验系统的响应速度降低，弹性振动也难以衰减，基于稳态测量思想的常规测力方法面临挑战。因此，有必要研究新的测力方法，提高脉冲风洞测力的准确性，更好地发挥其优势。

本文研究采用载荷辨识技术进行间接测力的方法。载荷辨识是根据测量得到的结构响应(应变、位移、速度或加速度等)，结合结构的动力学方程(或传递函数)反求结构所受的载荷历程。作为结构动力学的第二类反问题，载荷辨识技术获得了广泛的研究和应用[1-5]，其难点在于问题本身的不适定性，因此在求解时普遍使用正则化方法，文献[6]对此进行了较全面的总结。

载荷辨识应用于模型测力，不需要结构响应达到稳态，可以放松对天平刚度的要求和对模型质量的限制，同时，辨识得到的是载荷随时间的变化过程，能反映更丰富的试验动态信息，如发动机点火时的推力建立过程，这对于精细地研究高超声速飞行器的气动-推力特性具有重要价值。Simmons等[7]最早将载荷辨识技术用于激波风洞模型阻力测量，使用的应力波天平，后来又将该技术发展用于多分量同时测量[8-10]。考虑到脉冲燃烧风洞的试验时间远大于激波风洞(5ms左右)，本文的方法在试验系统建模、天平标定方面均和基于应力波天平的测力技术有所不同，并且提出了新的载荷辨识算法。

1试验系统的动力学建模

载荷辨识需已知系统的动态特性，所以首先建立试验系统的结构动力学方程，并希望方程的自由度尽量少，以降低后续的计算量。

图1　试验系统示意图 Fig.1 Schematic of the testing system

1.1试验系统结构组成

风洞测力试验系统主要由飞行器模型、天平、支架以及数据采集系统组成，对于结构动力学建模，仅考虑前三部分。由于飞行器模型一般比较长、比较重，同时，为了避开其腹部的推进流道，通常采用背部支撑的方式固定在风洞中，系统的剖面如图1所示。天平的浮动框与试验模型固连，天平的固定框与支架上端固连，支架下端固定于地面。在来流作用下，试验模型带动天平浮动框运动，使天平的弹性元件产生应变，利用应变片产生输出信号。

1.2建模方法

可以用有限元方法直接对整个试验系统进行建模，然后通过模态降阶得到低阶模型，但是，为了在动力学方程中保留模型的刚体自由度和直接使用天平的标定数据，在此采用子结构方法来建模。将系统分为试验飞行器、天平和支架三个子结构。由于试验时天平的浮动框与试验飞行器固连在一起，固定框与支架固连在一起，因此，在建模时把浮动框归入试验飞行器，把固定框归入支架，而天平子系统本身只考虑连接浮动框与固定框的弹性测量元件。

子结构采用Craig-Bampton方法[11](后面简称C-B方法)建模。C-B方法的子结构模态包括界面约束模态(后面简称约束模态)和固定界面正规模态(后面简称正规模态)，因此，首先要确定子结构间的连接界面，并根据需要作必要的简化。

前面已将天平浮动框归入试验飞行器、将天平固定框归入支架，所以试验飞行器与天平的连接面就是天平测量元件与浮动框的对接面，天平与支架的连接面就是测量元件与固定框的连接面。实际中，天平的浮动框和固定框的刚度远远大于测量元件的刚度，相对于弹性测量元件，两个框可近似看作刚体，于是它们与测量元件的对接界面均可简化为一个6自由度的点。将试验飞行器(含浮动框)的界面点记作点Ⅰ、天平(测量元件)在浮动框一侧的界面点记作点Ⅱ、天平(测量元件)在固定框一侧的界面点记作点Ⅲ、支架的界面点记作点Ⅳ。

1.2.1试验飞行器的模型

试验飞行器用有限元方法建模。为了将其与天平的对接面简化为一个点，在适当的位置，例如质心处，设置一节点作为主节点(即点Ⅰ)，将浮动框上与天平弹性元件对接面上的节点作为从节点，用刚性单元相连。在此基础上，用成熟的商业有限元软件可以直接进行子结构分析，输出子结构的质量和刚度矩阵，从而建立其动力学方程

(1)

这里，下标B(Boundary)表示界面约束模态，下标N(Normal)表示正规模态。ηⅠ,B是试验飞行器约束模态的位移向量，为6个刚体位移

(2)

ηⅠ,N为正规模态位移向量，假设取前nm阶正规模态，则

(3)

因此，飞行器子系统共有6+nm个自由度。因为约束模态均为刚体模态，所以子阵KⅠ,BB为零矩阵，而子阵MⅠ,BB为飞行器的刚体质量矩阵(参考点为点Ⅰ)，而fⅠ,B正是飞行器所受气动力和力矩向量(关于点Ⅰ的)。fⅠ,N是正规模态对应的广义力，其第Ⅰ个分量的计算式如下

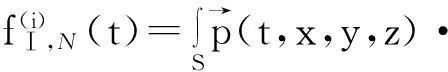
(4)

1.2.2天平子系统的模型

天平的浮动框和固定框分别归属飞行器和支架后，天平子系统仅剩下弹性测量元件，由于测量元件尺寸相对较小，质量也较轻，为简化模型，忽略其惯性，从而将天平子系统建模为无质量的广义弹簧，其与试验飞行器和支架分别有一个对接点(点Ⅱ和点Ⅲ)，所以天平子系统共12个自由度，其模型为12×12的刚度矩阵。简化模型示意图见图2。

虽然可以用有限元计算天平的刚度矩阵，但天平是试验系统的关键环节，实际中要经过校准，显然利用校准数据来得到其刚度矩阵将更为准确。

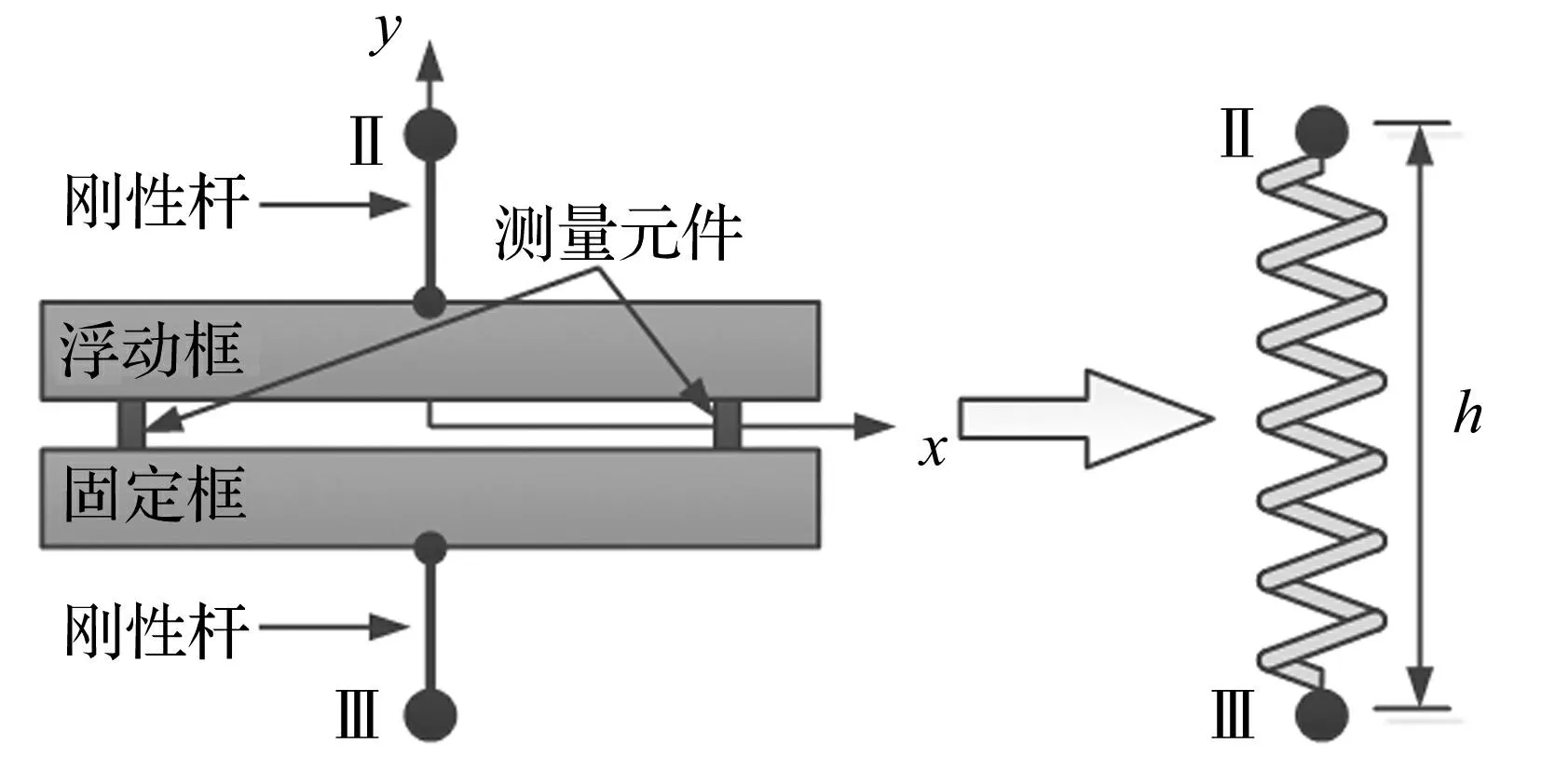
图2　天平子系统的力学模型 Fig.2 Mechanical model of the balance

点Ⅱ、点Ⅲ的位移向量分别记作

天平子系统的力学模型为

(5)

式中，fⅡ、fⅢ分别是作用于点Ⅱ、点Ⅲ的载荷向量，每个载荷向量包括3个力和3个力矩。在校准时，是将天平固定框完全约束，通过刚性足够的夹具与浮动框连接，然后在夹具上施加载荷，载荷施加点称为校心，一般位于天平的几何中心线上。在此，假设点Ⅱ即为校心。点Ⅲ选在同一中心线上位于固定框的一侧，与固定框刚性连接，与点Ⅱ之间的距离为h。那么，校准时的边界条件即为：点Ⅲ完全固定，在点Ⅱ施加校准载荷。于是在方程(5)中，ηⅢ=0，从而有

KⅡ,ⅡηⅡ=fⅡ

(6)

KⅢ,ⅡηⅡ=fⅢ

(7)

代入式(6)有

KⅡ,ⅡRⅡ=PⅡ

(8)

于是得到

(10)

利用式(7)和式(8)可得

KⅢ,ⅡRⅡ=-TB1PⅡ=-TB1KⅡ,ⅡRⅡ

(11)

所以有

KⅢ,Ⅱ=-TB1KⅡ,Ⅱ

(12)

因为刚度矩阵是对称的，所以有

KⅡ,Ⅲ=KTⅢ,Ⅱ=-KTⅡ,ⅡTTB1=-KⅡ,ⅡTTB1

(13)

现在尚有KⅢ,Ⅲ待求。假设解除点Ⅲ的所有约束，允许天平产生刚体运动，在点Ⅱ沿6个自由度依次施加微位移Δx、Δy、Δz、Δθx、Δθy、Δθz，写成位移向量矩阵

由于现在点Ⅲ自由，它要产生相协调的一组位移向量，记作ΔRⅢ，忽略二阶小量，易得

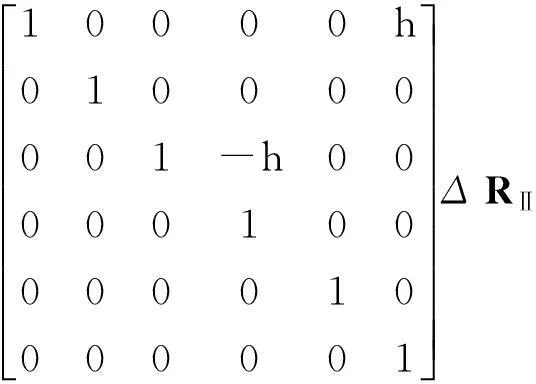
(14)

因为点Ⅲ不受力，将ΔRⅡ、ΔRⅢ代入式(5)的第二组方程，有

KⅢ,ⅡΔRⅡ+KⅢ,ⅢΔRⅢ=0

(15)

再利用式(14)可得

(16)

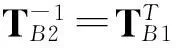
KⅢ,Ⅲ=TB1KⅡ,ⅡTTB1

(17)

至此，利用天平校准时的加载及位移测量数据可以计算出其刚度矩阵。天平校准时还要获取天平方程，即天平传感器(一般是应变计)输出与校心载荷的关系，这是常规天平校准的首要目的，具体过程在此不详述，假设已获得如下天平方程

v=NB,ⅡfⅡ

(18)

式中：v是天平输出(一般是电压)，其与载荷向量是等长的，系数矩阵NB,Ⅱ是方阵，且非奇异。现在需要推导天平输出与点Ⅱ、Ⅲ位移的关系。因为校准时固定框(点Ⅲ)被完全约束，所以ηⅢ=0，式(6)成立，将其代入式(18)得

v=NB,ⅡKⅡ,ⅡηⅡ≜SⅡηⅡ

(19)

这里，将SⅡ=NB,ⅡKⅡ,Ⅱ称为点Ⅱ对应的传感矩阵。尚需求点Ⅲ对应的传感矩阵，将其记作SⅢ，则两点都产生位移时，天平的输出应该是

v=SⅡηⅡ+SⅢηⅢ

(20)

如果给定点Ⅱ的位移ηⅡ，而让点Ⅲ自由运动，则根据式(14)有ηⅢ=TB2ηⅡ，此时天平仅有刚体位移，输出应该为零，根据式(20)有

SⅡηⅡ+SⅢTB2ηⅡ=0

(21)

所以有

(22)

代入式(20)，有

此即天平子系统的传感方程。

1.2.3支架子系统模型

支架子系统亦用有限元方法建模，其过程与试验飞行器子系统一样，需设置一节点作为主节点(即点Ⅳ)，选取固定框上与弹性元件对接处的所有节点为从节点，用刚性单元相连。在此基础上，用商业有限元软件执行子结构分析可以获取子结构的质量和刚度矩

阵，得到其动力学方程为

(24)

支架约束模态的位移向量为

假设正规模态取前ns阶，记为

则方程(24)共6+ns个自由度。

1.2.4系统模型综合

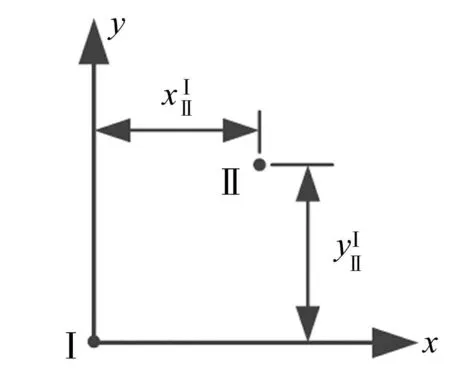
图3　点Ⅰ和点Ⅱ的相对位置 Fig.3 Position relationship of point Ⅰ and point Ⅱ

尽管各子结构之间的界面已简化为一个点，但是各子结构的界面点是为建模方便而选取的，相邻子结构的“界面”不一定重合，需要用刚性杆将其连接，以构成完整系统。

各子结构的界面点尽管不一致，但应该都是选在其对称面(x-y平面，见图1)内。假设点Ⅰ和点Ⅱ的相对位置如图3所示，则用刚性杆连接后，其位移(微量)向量之间存在如下关系

ηⅡ=

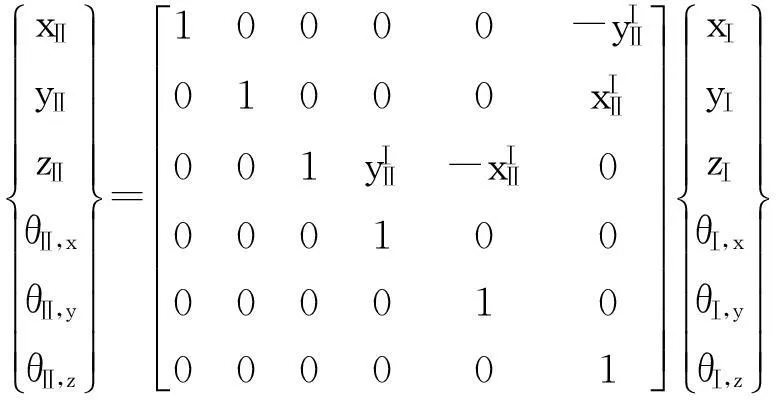
(25)

类似地，可建立点Ⅲ和点Ⅳ位移向量的关系

(26)

利用式(25)、(26)，可将三个子结构的方程(1)、(5)和(24)综合在一起，形成整个系统的动力学方程，其中独立的自由度向量只有ηⅠ,B、ηⅠ,N、ηⅣ,B、ηⅣ,N，列在一起记作

系统的动力学方程为

(27)

其中

K=

实际中，天平置于飞行器内部，是不受外载荷作用的，因此fⅡ和fⅢ均为零。支架外部可以加整流外罩进行遮挡，也不受气动载荷，因此fⅣ,B和fⅣ,N为零。非零载荷只有试验飞行器的气动载荷，其被分解为约束模态载荷和正规模态载荷，根据它们的定义，实际中前者是主要的，也是人们通常所指的气动载荷，后者则相对较小，而且不直接引起天平输出，因此可将fⅠ,N忽略，仅保留fⅠ,B。于是，试验系统的力载荷向量简化为

实际结构总是有阻尼的，考虑阻尼后系统动力学方程为

(28)

传感方程(23)也需要用η来表示，易得

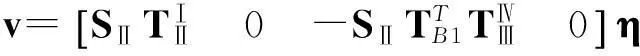
(29)

2载荷辨识模型

式(28)、(29)构成完整的试验系统动力学输入输出方程。通过扩维降阶将其变为状态空间形式

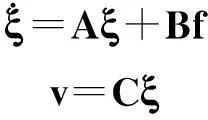
(30)

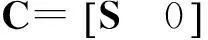
y=Rx

(31)

式中：输出y已知，输入x待求。

3载荷辨识方法

3.1子空间投影法

载荷辨识是典型的反问题，方程(31)通常是病态的，输出向量y中的噪声会使得解x严重偏离真解，失去利用价值，而实际中测量噪声(误差)是不可避免的。为了得到有意义的解，必须对其进行正则化，Tikhonov正则化方法[15-16]是最常用的，它用如下最小化问题的解作为问题(31)的近似解[17]

(32)

式中α(>0)是正则化参数。上式与如下问题等价

(33)

实际中，由于结构频率较高，测量的采样率也很高，若待辨识的时段稍长则矩阵R的规模会很大，而在优化选择正则化参数α的过程中，要反复求解式(33)，因此很难直接基于式(33)来求解。

为了使实际问题的求解更加可行，这里采用子空间投影法，将问题(32)的解限制在某个维数较低的解域上，从而降低求解规模。假设选定了一组基向量w1、w2、…、wk，将近似解x限制在由其张成的k维空间Wk上，即

x∈Wk=span{w1,w2,…,wk}

令

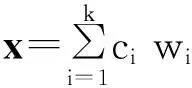
(34)

(35)

其等价问题为

(WTkRTRWk+αWTkWk)cα=(RWk)Ty

(36)

方程(36)的系数矩阵大小为k×k，通常k远远小于R的行数和列数，求解规模大大降低。

显然，投影子空间的选择，也就是投影基向量w1、w2、…、wk的选择是影响近似解好坏的关键，为了逼近原问题的解，该子空间需尽量包含系数矩阵R前k个右奇异向量的信息。Krylov子空间具备这样的特性[18]。k维Krylov子空间的定义如下[16, 18]

Krylov子空间的基向量可以按定义直接计算，但采用Golub-Kahan双对角迭代法[19]可以得到性质更好的基向量，并为问题的求解带来方便。基本算法如下：

w0=0，β1z1=y

对i=1,2,3,…,k，执行以下迭代：

αiwi=RTzi-βiwi-1

βi+1zi+1=Rwi-αkzi

式中，实数αi、βi的作用是分别使向量wi和zi单位化。迭代的结果得到如下关系式

RWk=Zk+1Bk

(37)

式中，

并且，Wk、Zk+1矩阵各自的列向量是相互正交的单位向量。将式(37)代入式(36)并利用Wk、Zk+1的正交性质，式(36)可简化为

(BTkBk+αI)cα=BTkZTk+1y

(38)

根据前面的迭代算法，y=β1z1，所以BTkZTk+1y=β1BTkZTk+1z1=β1BTke1，其中e1标准欧氏空间的第1个向量。于是，式(38)进一步简化为

(BTkBk+αI)cα=β1BTke1

(39)

注意BTkBk+αI为三对角矩阵，因此上式可以用追赶法快速求解。得到cα后，最终解由下式给出

(40)

3.2确定正则化参数的L曲线准则

(41)

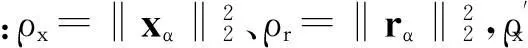
(42)

式中zα是如下问题的解

(43)

当采用子空间投影后,有

(44)

(45)

为减小计算量，zα也用子空间投影法来近似计算，即令

zα≈Wkζ

(46)

从而将问题(43)变为如下容易求解的问题

(47)

于是，曲率的κ(α) 计算量大大降低，使得L曲线准则容易实施。

3.3子空间维数的确定方法

现在讨论如何确定适当的子空间维数k。显然，对同一个正则化参数α，取不同的子空间维数，得到的正则化解是不同的，因此，不同子空间维数下作出的L曲线是不重合的。但是，由于k维Krylov子空间的基向量具有逼近矩阵R前k个右奇异向量的性质，随着k的增加，后面的基向量对正则解的贡献逐渐减弱，所以L曲线本身随k的增加将趋于收敛。在此，取如下指标作为判断L曲线收敛的依据

J=‖xα‖2·‖rα‖2

(48)

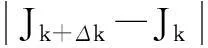
3.4求解算法

根据前面的讨论，对问题(31)完整的求解算法包括两步，首先用3.3节的方法确定合适的子空间维数，然后在该子空间下用3.2节的L曲线准则确定最优的正则化参数，并得到对应的正则化解。第一步的详细算法流程为：

(1)给定初始子空间维数k0和维数的增量Δk；给定i0和nα，计算出αi序列；给定参数ε；

(2)执行k0步Golub-Kahan双对角迭代，得到式(37)的各矩阵；

(3)针对每个αi求解方程(39)，由(44)、(45)式得到‖xα‖2、‖rα‖2，计算指标函数值序列J(αi,k)，找出最小值对应的序号ik和最小值Jk；

(4)将当前子空间下的结果ik、Jk与上一步的结果ik-Δk、Jk-Δk作比较，若满足条件

终止，得到子空间维数k；否则往下执行；

(5)k←k+Δk，继续执行Δk步Golub-Kahan，扩充子空间，转到第3步。

确定了子空间维数后，对应低维正则化问题的L曲线就确定了，现在需要寻找最大曲率点的正则化参数。这时，L曲线上各点的曲率κ是参数α的函数，即式(41)，可以采用一维搜索算法[23]求函数κ(α)的近似极大值解，起点可以取前面确定子空间维数时得到的αik，具体算法在此不再详细列出。得到问题(39)的正则解cα后代入式(40)，最终得到问题(31)的正则化解。

4数值算例

考虑一个虚拟的试验飞行器及其测力系统，其模型、天平及支架如图4所示。飞行器长2.1m，材料为超硬铝，重255.24kg，天平和支架为钢材。

图4　试验系统三维图 Fig.4 View of the testing system

用有限元法直接对全系统建模，称其为全阶模型，作为简化模型的对比基准。天平也用有限元建模，通过静力计算，模拟实际校准过程，用得到的数据建立简化模型的刚度矩阵。每个测量通道取四个点的应变组成惠氏电桥，根据经验设置应变片的灵敏度，将应变转化为电压，据此计算天平传感矩阵。

4.1模态计算结果

用有限元软件分别对试验飞行器和支架进行子结构分析并输出质量、刚度矩阵，得到子结构动力学模型。其中试验飞行器取7个正规模态，支架取6个正规模态，加上各自的6个约束模态，系统简化模型共25个自由度，而全阶模型的节点数超过30万，自由度超过100万。对全阶模型和简化模型进行模态分析，得到的前10阶固有频率列于表1，可见简化模型纵向和横侧向的前两阶频率精度都是比较高的。

表1　固有频率计算结果对比

4.2瞬态响应结果

某脉冲燃烧风洞典型的来流动压变化曲线如图5所示(对原始数据作低通滤波的结果)。现在计算试验系统在其作用下的天平输出。对于全阶模型，用工程方法[24]计算试验飞行器表面气流压力分布，模拟真实的受力状态。对于简化模型，先将飞行器的压力分布系数积分，得到合力和力矩(关于质心)系数，再作为集中力加载。计算时，两种模型的阻尼均以模态阻尼方式施加，各阶阻尼比均取0.005。

假设侧滑角为零，则气动载荷只有阻力、升力和俯仰力矩。在图5所示来流作用下，全阶模型和简化模型得到的天平三个通道的输出对比如图6所示，低频信号吻合良好。高频响应的误差来自两个方面，一是简化模型本身的高频特性误差较大，二是两种模型的加载方式不同，全阶模型加载的是分布力，而简化模型加载的是等效集中力，忽略了式(1)中的fⅠ,N。

由模态分析和瞬态响应结果的对比，说明低阶简化模型反映了试验系统主要的动力学特性。

图5　典型的风洞来流动压曲线 Fig.5 The history of dynamic pressure of the flow

图6　瞬态响应对比 Fig.6 Comparison of transient responses

图7　载荷辨识结果对比 Fig.7 Comparison of the identified loads

4.3载荷辨识结果

以全阶模型计算的瞬态响应当作试验测量结果，对飞行器所受载荷历程进行辨识。输出采样率取5 000Hz，采样时长0.8s，有3个输出，3个待辨识载荷，原始问题式(31)中矩阵R的大小为12 000×12 003。根据对真实试验测量信号的统计分析，测量噪声的标准差约为0.002 3mV，在此按0.005mV给计算输出加白噪声。计算时，初始子空间维数取550，增量取10，子空间收敛判定参数ε取0.001，正则化参数序列取10-30～10-20之间15个对数均布的点。最终确定的子空间维数为920，远低于原始问题的维数，最优正则化参数为α=1.453 8×10-24。3个载荷的辨识结果与真实值的对比见图7，二者吻合良好。定义辨识误差为

(49)

对于辨识结果中的噪声，可以通过适当的平滑处理来有效地降低。图8是对阻力曲线用20点平均法进行平滑处理后的结果，噪声大大降低，但载荷本身的低频信息仍得以保留。

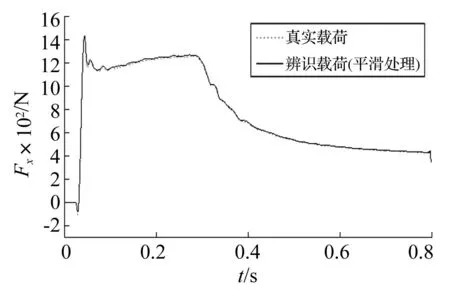
图8　平滑后的阻力曲线 Fig.8 Smoothed drag force

现在考察测量信号中不同噪声强度对辨识结果的影响。分别取噪声的标准差为0.002mV、0.004mV、0.008mV、0.016mV、0.032mV和0.064mV时得到的辨识结果如表2所示。其中，辨识误差取的是3个载荷的平均误差。可见，随着噪声强度的增加，子空间维数在减小、正则化参数在增大，即对问题的正则化作用不断加强，相应地，辨识误差也在逐渐变大。均符合预期的规律。

表2　噪声对辨识结果的影响

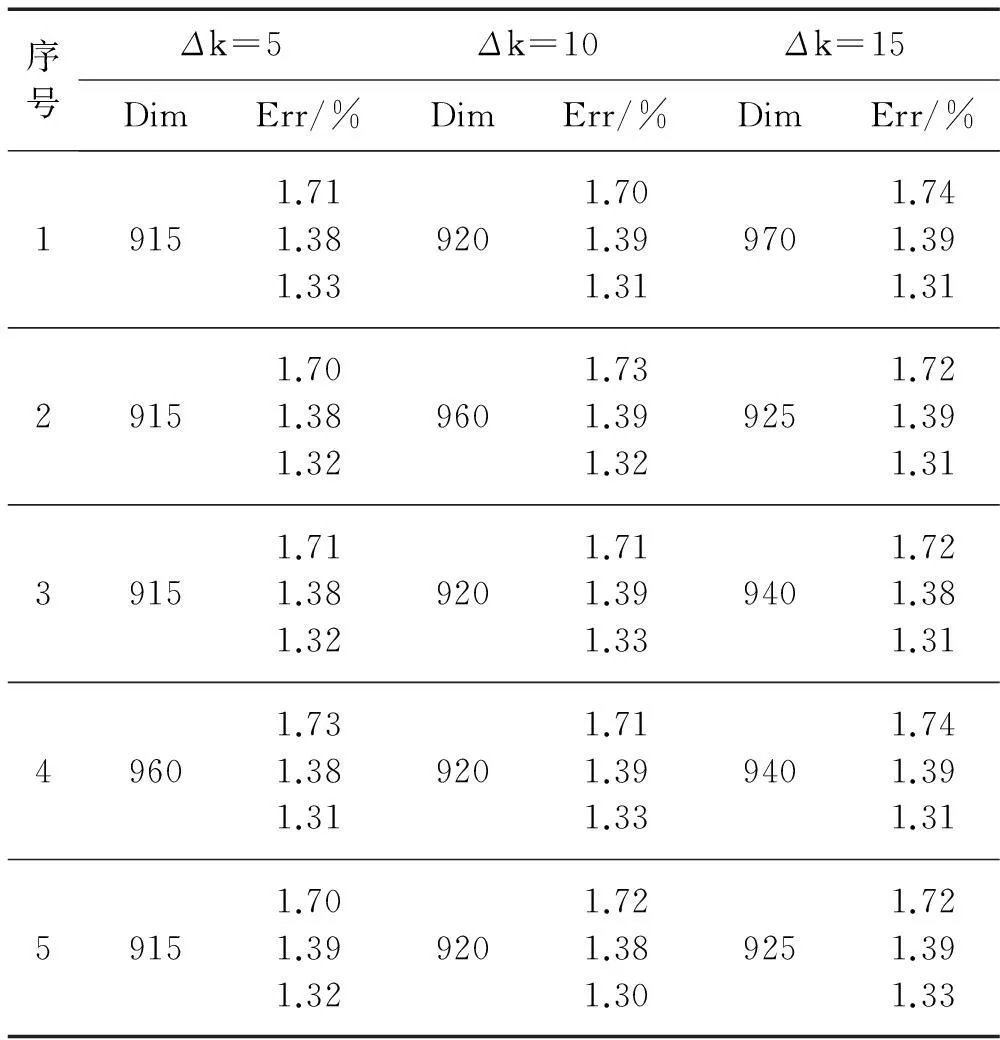
表3　不同计算条件下的结果

4.4算法的稳定性分析

输出测量信号中的噪声是随机的，因此算法每次执行得到的结果亦可能有所不同，包括子空间大小、正则化参数以及辨识结果的精度。但是噪声的统计特性基本不变，所以，对于一个稳定的算法，计算结果不应有大幅波动。另外，子空间维数增量Δk和正则化参数序列αi的设置也会对计算过程和结果产生影响。

现分别取Δk等于5、10、15，每种情况执行5次辨识算法，每次的噪声随机生成，正则化参数序列也在10-30～10-20之间随机生成15个点。计算结果如表3所示，可见尽管子空间维数有所波动，但变化不大，而辨识结果的精度也变化很小，表明算法是稳定、鲁棒的。

5结论

本文应用子结构综合法，并充分利用天平校准数据，建立了试验系统的低维动力学模型，可以比较准确地反映系统的低频动态特性。通过对动力学方程进行时域离散，建立起试验飞行器气动力(力矩)与天平响应之间的线性关系方程，用来进行气动载荷的辨识。

将Tikhonov正则化方法与基于Krylov子空间的投影法结合，把高维的不适定问题变为低维的适定问题，并充分利用Golub-Kahan双对角迭代算法的性质，大大提高了求解效率。

提出了确定投影子空间大小的方法，该方法仅需计算低维问题的正则解及剩余向量的范数，计算简单。子空间维数确定后，问题的规模大大减小，再应用L曲线准则确定最优的正则化参数，计算量大为降低，用一维搜索算法可快速得到最优参数。数值试验表明，算法具有良好的稳定性。

在对试验系统进行建模时，结构的阻尼参数是假定已知的，而实际中通常难以准确知道结构的阻尼参数，因此，利用测量响应，对载荷和阻尼参数同时进行辨识是值得进一步研究的课题。

参考文献

[1]HollandsworthPE,BusbyHR.Impactforceidentificationusingthegeneralinversetechnique[J].InternationalJournalofImpactEngineering, 1989, 8(4): 315-322.

[2]ChoiK,ChangFK.Identificationofimpactforceandlocationusingdistributedsensors[J].AIAAJournal, 1996, 34(1): 136-142.

[3]MaoYM,GuoXL,ZhaoY.Astatespaceforceidentificationmethodbasedonmarkovparametersprecisecomputationandregularizationtechnique[J].JournalofSoundandVibration, 2010, 329(15): 3008-3019.

[4]HwangJS,KareemA,KimH.Windloadidentificationusingwindtunneltestdatabyinverseanalysis[J].JournalofWindEngineeringandIndustrialAero-dynamics, 2011, 99(1): 18-26.

[5]RonasiH,JohanssonH,LarssonF.Anumericalframeworkforloadidentificationandregularizationwithapplicationtorollingdiscproblem[J].Compu-ters&Structures, 2011, 89: 38-47.

[6]王林军. 正则化方法及其在动态载荷辨识中的应用[D]. 长沙：湖南大学, 2011.

[7]SandersonSR,SimmonsJM.Dragbalanceforhypervelocityimpulsefacilities[J].AIAAJournal, 1991, 29(12): 2185-2191.

[8]SmithAL,MeeDJ,DanielWJT,etal.Design,modellingandanalysisofasixcomponentforcebalanceforhypervelocitywindtunneltesting[J].ComputersandStructures, 2001, 79: 1077-1088.

[9]RobinsonMJ,MeeDJ,TsaiCY,etal.Three-componentforcemeasurementsonalargescramjetinashocktunnel[J].JournalofSpacecraftandRockets, 2004, 41(3): 416-425.

[10]RobinsonMJ,HannemannK,SchrammJM.Designandimplementationofaninternalstresswaveforcebalanceinashocktunnel[J].CEASSpaceJournal, 2011, (1): 45-57.

[11]CraigRR,Jr,BamptonMCC.Couplingofsubstructuresfordynamicanalysis[J].AIAAJournal, 1968, 6: 1313-1319.

[12]郭杏林, 毛玉明, 赵岩, 等. 基于Markov参数精细积分法的载荷识别研究[J]. 振动与冲击, 2009, 28(3): 27-31.

GUOXin-lin,MAOYu-ming,ZHAOYan,etal.Loadidentificationbasedonprecisetime-stepintegrationforMarkovparameters[J].JournalofVibrationandShock, 2009, 28(3): 27-31.

[13]ZhongWX,WilliamsFW.Aprecisetimeintegrationmethod[J].JournalofMechanicalEngineeringScience, 1994, 208: 427-430.

[14]韩旭, 刘杰, 李伟杰, 等. 时域内多源动态载荷的一种计算反求技术[J]. 力学学报, 2009, 41(4): 595-602.

HANXu,LIUJie,LIWei-jie,etal.Acomputationalinversetechniqueforreconstructionofmultisourceloadsintimedomain[J].ChineseJournalofTheoreticalandAppliedMechanics, 2009, 41(4): 595-602.

[15]CalvettiD,MorigiS,ReichelL,etal.Tikhonovregulariza-tionandtheL-curveforlargediscreteill-posedproblems[J].JournalofComputationalandAppliedMathematics, 2000, 123(1-2): 423-446.

[16]LampeJ,ReichelL,VossH.Large-scaletikhonovregulari-zationviareductionbyorthogonalprojection[J].LinearAlgebraanditsApplications, 2012, 436(8): 2845-2865.

[17]BauerF,LukasMA.Comparingparameterchoicemethodsforregularizationofill-posedproblems[J].MathematicsandComputersinSimulation, 2011, 81(9): 1795-1841.

[18]HansenPC.Discreteinverseproblems:Insightandalgorithms[M].Philadelphia:SocietyforIndustrialandAppliedMathematics, 2010.

[19]GolubG,KahanW.Calculatingthesingularvaluesandpseudo-inverseofamatrix[J].JournaloftheSocietyforIndustrial&AppliedMathematics,SeriesB:NumericalAnalysis, 1965, 2(2): 205-224.

[20]HansenPC,O’learyD.Theuseofl-curveintheregulariza-tionofdiscreteill-posedproblems[J].SIAMJournalonScientificComputing, 1993, 14: 1487-1503.

[21]VogelCR.Computationalmethodsforinverseproblems[M].Philadelphia:SIAM, 2002.

[22]RegińskaT.Aregularizationparameterindiscreteill-posedproblems[J].SIAMJournalonScientificComputing, 1996, 17(3): 740-749.

[23]袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京; 科学出版社. 1997: 56-107.

[24]BonelliF,CutroneL,VottaR,etal.Preliminarydesignofahypersonicair-breathingvehicle[C]. 17thAIAAInternationalSpacePlanesandHypersonicSystemsandTechnologiesConference,SanFrancisco,California, 11-14April, 2011.