一种基于残周期正弦拟合的冲击峰值计算方法

一种基于残周期正弦拟合的冲击峰值计算方法

梁志国1,李新良1,朱振宇1,2

(1.北京长城计量测试技术研究所计量与校准技术重点实验室，北京100095;2.天津大学精密仪器与光电子工程学院，天津300072)

摘要：针对半正弦冲击波形峰值幅度的计算，提出了一种基于残周期正弦曲线拟合的最小二乘计算方法，通过在脉冲测量波形中截取峰值附近近似于半正弦部分的峰值波形，使用残周期正弦曲线拟合方法计算获得冲击峰值幅度。它具有操作简捷易行、收敛性好的特点，并可以通过拟合残差有效值来判定拟合效果的优劣。该方法直接使用截取的峰值波形原始数据进行计算，不需要用滤波器对波形数据进行预处理，从而避免了冲击计量中常用的数字滤波给峰值计算结果带来的影响，可以获得更加客观准确的校准结果。通过在实际校准实验波形上的计算，并与以往计算方法进行了比较，验证了所述方法的有效性和切实可行性。

关键词：脉冲；峰值幅度；正弦曲线拟合；参数估计；校准；评价

中图分类号:TM930.14文献标志码：A

基金项目：国家十二五预研基金资助项目(51309020301)

收稿日期：2013-08-29修改稿收到日期：2014-01-02

Novelcalculationmethodforpeakofimpulsewaveformsbasedonpartialsinusoidalcurve-fitting

LIANG Zhi-guo1,LIXin-liang1,ZHUZhen-yu1,2(1.NationalKeyLaboratoryofMetrologyandCalibrationTechnology,ChangchengInstituteofMetrologyandMeasurement,Beijing100095,China;2.CollegeofPrecisionInstrumentandOpto-ElectronicsEngineering,TianjinUniversity,Tianjin300072,China)

Abstract:Aiming at the peak calculation of half-sine style impulse, a novel calculation method based on partial sinusoidal curve-fitting was presented. A half-sine wave part near the impulse peak was taken out from acquisition data, and then the partial sinusoidal curve-fitting was applied to get the impulse peak value. The method has the specialties of being easy to use, good convergence, and so on. Through the curve-fitting error analysis, one can compare the different curve-fitting results, and know which is better. The method presented uses the sampling data to calculate the impulse peak directly, without any filtering for pre-pressing, so, it can attain the more precise and more impersonal peak results. In a group of impulse calibration experiments, comparing with traditional methods, both the correctness and the feasibility of the pulse peak calculation method were proved.

Keywords:impulse;peakamplitude;sinusoidalcurve-fitting;parameterestimation;calibration;evaluation

冲击是一种常见的物理现象，人们用落槌、霍普金森冲击机、压缩空气炮等许多手段可以产生冲击波形，其峰值、脉宽等测量和计算是冲击测量中的基本问题[1-9]。

冲击波形属于脉冲波，而脉冲峰值的计算与确定是脉冲测量中的基本问题，为了避免噪声、阶跃响应过冲、振玲等对峰值计算的影响，IEC标准里定义了脉冲的“顶”(top)、“底”(base)等基本术语，用来描述脉冲的峰值和谷值，并以众数法来确定脉冲的“顶”和“底”[10-11]。对于方波等“顶”与“底”较平坦的脉冲波形，该定义及方法具有优良的适应性。但对于冲击产生的类似于半正弦型脉冲，其峰值往往不平坦、不规则、且采样测量点也不够多，这时，使用众数法常常会遇到适应性较差的问题，最直接的表现就是测量重复性较差。通常人们的做法是对测量波形进行滤波，将冲击波形的峰值滤得比较平坦后再直接寻找最大值确定峰值[5-6]。然而，滤波带宽的选取，以及滤波后是否给峰值造成较大影响的判定，一直是困扰冲击计量的基本问题，并使得冲击测量的准确度一直难以提高，约为5%左右[12]。

本文后续内容，主要是针对半正弦类冲击波形峰值计算的问题，提出一种模型化方法，以半正弦拟合方法确定冲击波形的峰值，并试图在不使用滤波器的情况下，直接以原始采集波形数据进行最小二乘曲线拟合，获得半正弦冲击波形的峰值，以期提高测量准确度和重复性。

1测量原理

冲击波形，在很多时候人们也称其为半正弦冲击波形，这主要是从形状上看，其近似于正弦波的一半而已，在处理方式方法上，从未将其与正弦波建立起联系。其最主要的原因可以归纳为两点：①完整的冲击波形形状与半正弦波形通常的差距非常大，仅仅在峰值附近的一个区间内，其外观与半正弦有些类似，即便如此，冲击波形的上升沿与下降沿两部分也并不对称，因而很难严格表述为“半正弦”波形；②使用“半正弦”模型表述冲击波形时，由于是“半正弦”而波型欠完整，使得通常很难确定波形参数。

残周期正弦波四参数拟合方法出现后，使得人们可以对“半正弦”类冲击波形按正弦模型方式进行处理，其中需要的前提仅仅是将冲击波形中与正弦波形差异较大的部分舍去而已。其具体过程如下：

(1)使用冲击激励源产生半正弦冲击激励，用传感器及配套波形数据采集系统进行波形测量，获得完整的冲击测量波形[13]；

(2)用比较法获得冲击波形的最大值和最小值；

(3)截取最大值和最小值之间近似半正弦部分波形用于峰值计算；

(4)将用于峰值计算部分波形按残周期正弦波拟合方法进行最小二乘波形拟合[14]。设用于波形拟合计算的采样序列为x1,x2,…,xn。其正弦波形最小二乘拟合曲线的函数表达式为：

y(i)=A·cos(ω·i+φ)+D

拟合残差有效值为：

式中:A为拟合正弦波形幅度；ω为拟合正弦波形角频率；φ为拟合正弦波形初始相位；D为拟合正弦波形直流分量；ρ为拟合残差有效值。当采样序列中仅含有噪声因素误差时，ρ即为叠加在正弦波形之上噪声的实验标准偏差。则可得冲击波形峰值估计值为：A+D。以拟合残差有效值ρ判断比较拟合优劣，并以此对所获峰值结果进行判断。

2校准装置及工作过程

如图1所示，加速度一次冲击校准装置主要由冲击机、差动式光栅激光干涉仪、数字示波器和计算机系统组成。各部分工作过程简介见图1。

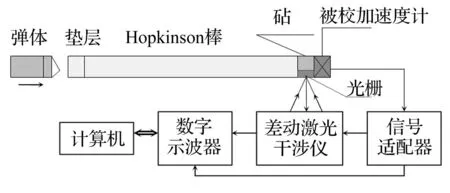
图1　加速度一次冲击校准装置框图 Fig.1 Calibration device of primary shock

Hopkinson冲击机，使用Hopkinson棒，在棒中产生应力波。在距激励端面几倍棒直径远处，应力波的波振面实际上变成了平面波。只要棒的长度与直径之比充分大，用Hopkinson冲击机，在校准端面可以获得波形良好，横向运动小的冲击过程。

差动式激光干涉仪用于测量含有光栅运动速度信息的多普勒频移信号，并传给数字示波器。数字示波器用于采集多普勒信号和记录被校加速度计输出信号，并转换为数字信号。

其工作过程如图1所示，使用Hopkinson冲击机对Hopkinson棒发射弹体，产生冲击加速度，同时作用于光栅和被校加速度传感器，被校加速度传感器测得的信号经信号适配器后被数字示波器采集。光栅位移经差动激光干涉仪产生具有多普勒效应的调频信号，该调频信号被数字示波器采集；对该调频信号进行频率解调后，可获得作用于加速度传感器上的速度值和加速度值[13]。

3实验验证

使用350B04型冲击加速度传感器(编号11024)和PCBF482A型放大器在上述加速度一次冲击校准装置所做实验，获得如图2所示的校准曲线波形[15-16]。

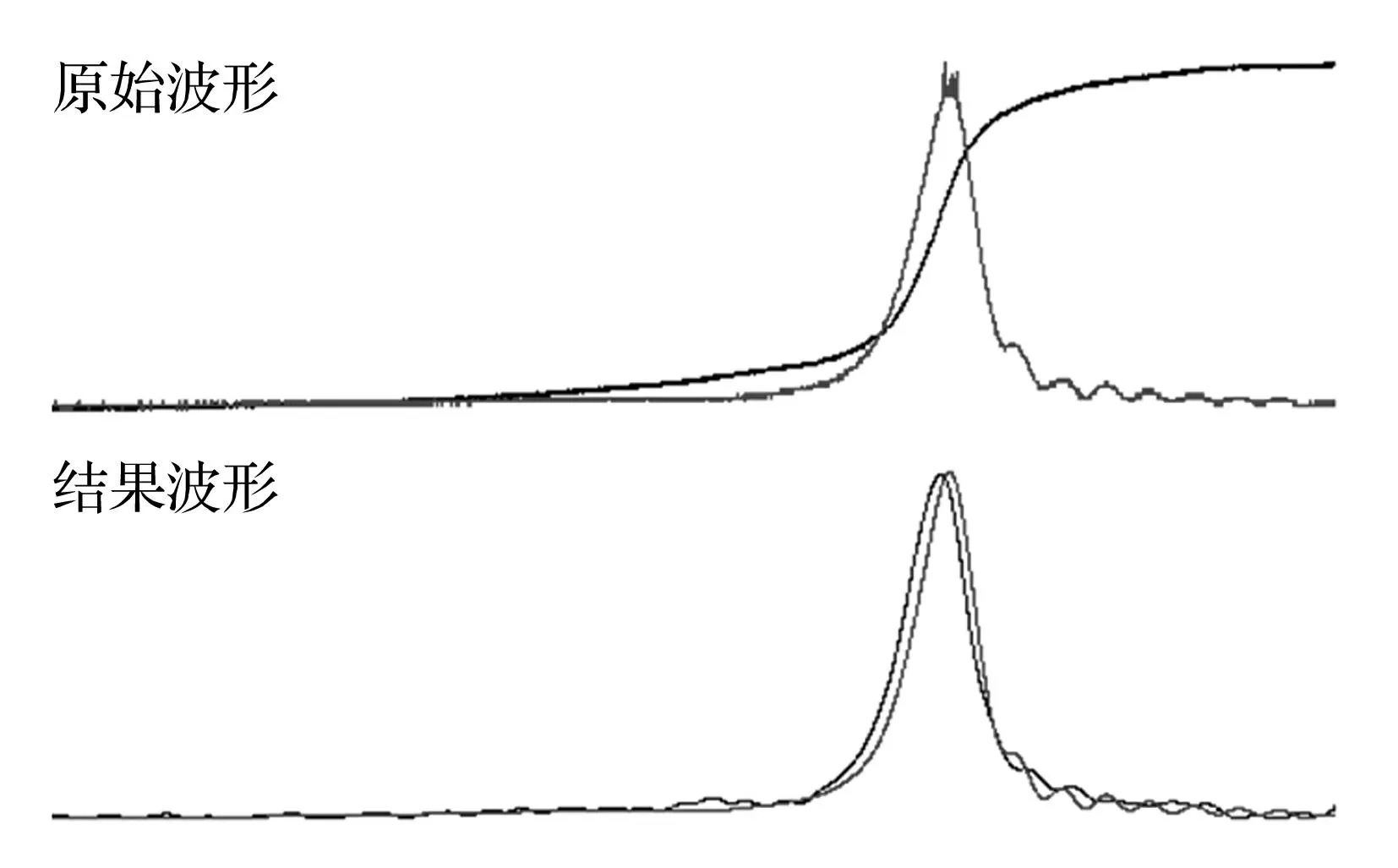
图2　冲击加速度传感器校准曲线 Fig.2 Acceleration waveform of impulse

图2上部是加速度传感器输出的半正弦冲击加速度波形和由激光干涉仪输出的阶跃速度波形，下部是经过带宽20kHz的数字滤波器滤波后的冲击加速度波形和由冲击速度微分获得的冲击加速度校准波形。

所使用的采集设备为TDS544A型数字示波器。双通道采样时，采样率6.25MSps，8BitsA/D，存储深度50kSamples/ch，模拟带宽500MHz，最小电压分度1mV/div。放大器归一化系数为1，放大倍数1，截止频率为30kHz。

加速度传感器的标称灵敏度为0.940 0mV/g，经按照检定规程校准获得的校准灵敏度为1.006 2mV/g，校准脉冲峰值3 221.14g，脉冲电压值为3.241V，所用数字滤波器带宽20kHz。这里使用的是直接读取法获得的加速度峰值[16]。

将图2所述波形按时间刻度重新绘制曲线如图3所示。

按本文上述方法进行处理，截取上3/4部分脉冲，使用残周期拟合方法获得拟合曲线与测量曲线如图4所示[14]，拟合正弦峰值为：A= 0.959 759V，拟合正弦直流偏移为：D= 2.422 325V；拟合残差有效值为：ρ=91.868 92mV；则拟合脉冲峰值为：3.382 084V。

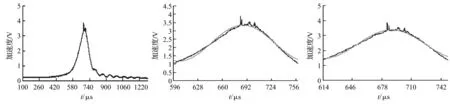
图3 冲击加速度传感器校准曲线Fig.3Accelerationwaveformofimpulse图4 冲击加速度波形及拟合曲线(3/4幅度)Fig.4Partialaccelerationwaveformofimpulseandcurve-fitting图5 冲击加速度波形及拟合曲线(2/3幅度)Fig.5Partialaccelerationwaveformofimpulseandcurve-fitting

按本文上述方法进行处理，截取上2/3部分脉冲，使用残周期拟合方法获得拟合曲线与测量曲线如图5所示，拟合正弦峰值为：A=1.085 737V，拟合正弦直流偏移为：D=2.265 4V；拟合残差有效值为：ρ=108.107 1mV；则拟合脉冲峰值为：3.351 137V。

按本文上述方法进行处理，截取上1/2部分脉冲，使用残周期拟合方法获得拟合曲线与测量曲线如图6所示，拟合正弦峰值为：A= 0.7321408V，拟合正弦直流偏移为：D= 2.675 251V；拟合残差有效值为：ρ= 70.103 34mV；则拟合脉冲峰值为：3.407 392V。

图6　冲击加速度波形及拟合曲线(1/2幅度) Fig.6 Partial acceleration waveform of impulse and curve-fitting

4讨论

由上述计算过程可见，使用本文所述方法，在脉冲峰值分别截取3/4、2/3和1/2等不同幅度计算半正弦脉冲时，获得的计算结果波动仅为1.6%，是一个非常良好的结果。不仅如此，本文所述方法的最大优势是可以通过拟合残差有效值来判断拟合效果的优劣，并针对不同截取范围所获得的拟合峰值，给出哪一个更可靠的量化判据，从图4~图6的三个曲线段的拟合结果来看，由于图6曲线的拟合残差有效值最小，故可以认定图6拟合所获得的峰值结果3.407 392V更为符合实际，也更可靠。

而使用以往方法经滤波获得的校准结果峰值3.241V比本文方法小，分析应该是使用滤波器滤除噪声和尖峰毛刺引起了峰值变化造成的结果。从而证明本文方法不使用滤波而直接用残周期正弦曲线拟合获取脉冲峰值的优越性。在脉冲峰值比较平滑时，本文方法能获得更加稳定良好的拟合结果。

尽管如此，在高加速度传感器计量校准中，由于冲击波形往往伴有畸变和不规则，使用本文方法会需要进一步判断和取舍。例如图7是另一种8309型高加速度传感器(其电荷灵敏度0.047 8pC/g)在38 737.44g条件下的校准结果曲线，从图中可见，该冲击波形在上升沿和峰值处均有畸变，它距离半正弦的理想情况有一定差异，使用本文方法虽然仍可以获得拟合峰值，但拟合残差有效值将变大。这时，需要人们首先判定截取哪一段波形用于峰值拟合计算，并且峰值处的“峰”如何对待和定义，这个问题解决后，计算问题将很容易通过本文方法获得有效结果。

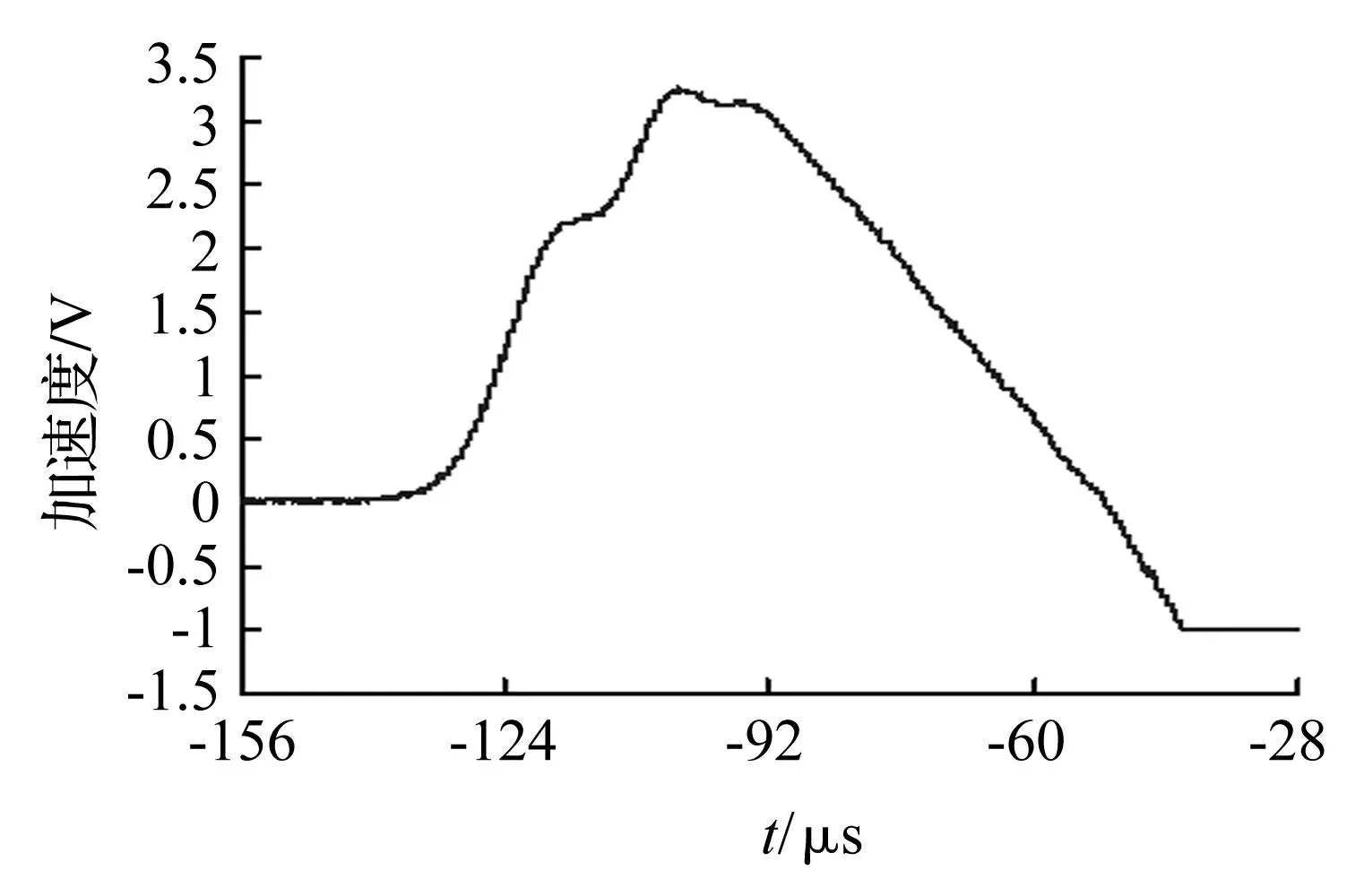
图7　 8309冲击加速度传感器校准曲线 Fig.7 Acceleration waveform of impulse for model 8309 transducer

在峰值定义明确后，峰值计算从本质上讲是一个曲线拟合问题，实际上，通过多项式拟合也能获得较好的效果，但多项式拟合后，寻找峰值需要求根，是一个比较复杂繁琐的工作，并且多项式本身还有定阶等问题，不如本文方法简便，由于本文方法对所有峰值均使用一个尺度，更容易执行、判断和比较。

5结论

本文针对半正弦冲击波形的峰值幅度计算，提出了一种基于残周期正弦波曲线拟合的峰值计算方法，其特点是以总体最小二乘方式获得峰值，避免峰值噪声、毛刺尖峰等给传感器测量曲线峰值估计带来的影响，并且可以利用拟合残差有效值来辅助判定峰值估计的可信程度。同时，不需要使用滤波器进行预先处理，直接使用原始波形数据进行计算，也避免了滤波器特性给峰值估计带来的附加影响。该方法具有鲁棒性优良、操作简捷有效、收敛性良好，可望被应用到脉冲计量校准、测试的实际工作中，用于脉冲峰值的计算和估计。由于高斯形状脉冲波形与半正弦形状差异不大，故本文上述方法也有望用于高斯形状脉冲峰值的计算中。

参考文献

[1]向红，汤伯森.L-P摄动法在跌落冲击问题中的应用[J].振动与冲击，2002，21(1)：39-42.

XIANGHong,TANGBo-sen,ApplicationofL-Pperturbationmethodindroppingshockproblem[J].JournalofVibrationandShock，2002，21(1)：39-42.

[2]卢富德，陶伟明，高德.具有简支梁式易损部件的产品包装系统跌落冲击研究[J].振动与冲击，2012，31(15)：79-81.

LUFu-de,TAOWei-ming,GAODe.Dropimpactanalysisonitempackingsystemwithbeamtypeelasticcriticalcomponent[J],JournalofVibrationandShock，2012，31(15)：79-81.

[3]高德，卢富德.基于杆式弹性易损部件的非线性系统跌落冲击研究[J]. 振动与冲击，2012，31(15)：47-49.

GAODe,LIUFu-de.Dropimpactanalysisofpackagingsystemwithbartypeelasticcriticalcomponents[J].JournalofVibrationandShock，2012，31(15)：47-49.

[4]陈安军.非线性包装系统跌落冲击问题变分迭代法[J].振动与冲击，2013，32(18)：105-107.

CHENAn-jun.Variationaliterationmethodfordroppingshockproblemofacubicnon-linearpackingsystem[J].JournalofVibrationandShock，2013，32(18)：105-107.

[5]ISO16063-13-2001(E),Methodsforthecalibrationofvibrationandshocktransducers-Part13:Primaryshockcalibrationusinglaserinterferometry[S].InternationalOrganizationforStandardization,pp11.

[6]GB/T20485.13-2007, 振动与冲击传感器校准方法——第13部分：激光干涉法冲击绝对校准.北京：中国标准出版社，2008.

[7]JJG791-1992，冲击力法冲击加速度校准装置[M].北京：中国计量出版社，1993,3，9.

[8]JJG632-1989，动态力传感器[M].北京：中国计量出版社，1990,5，7.

[9]JJG497-2000，碰撞试验台[M].北京：中国计量出版社，2000,7，5.

[10]IECStandard, 469-2,Pulsetechniquesandapparatus, (part2:Pulsemeasurementandanalysis,generalconsiderations)[M].InternationalElectricalCommission, 1987: 21-22.

[11]GB9318-1988，脉冲信号发生器测试方法[M].北京:电子工业出版社，1990年4月.

[12]ISO16063-1-1998(E),Methodsforthecalibrationofvibrationandshocktransducers-Part1:BasicConcepts,InternationalOrganizationforStandardization,pp17.

[13]梁志国，李新良，连大鸿.激光干涉法一次冲击加速度校准[J].电子测量与仪器学报，2006，20(1)：68-72.

LIANGZhi-guo,LIXin-liang,LIANDa-hong.Primaryshockcalibrationusinglaserinterferometry[J].JournalofElectronicMeasurementandInstrument,Feb. 2006, 20(10): 68-72.

[14]梁志国，孟晓风.残周期正弦波形的四参数拟合[J].计量学报，2009，30(3): 245-249.

LIANGZhi-guo,MENGXiao-feng.Acurve-fitarithmeticoffour-parametersinewaveforpartialperiod[J].ActaMetrologicaSinica,May, 2009, 30(3): 245-249.

[15]JJF1153-2006，冲击加速度计(绝对法)校准规范.北京：中国计量出版社，2007年3.

[16]JJG233-2008，压电加速度计检定规程.北京：中国计量出版社，2008年12月.

第一作者陶永康男，博士生，1989年12月生

通信作者董景新男，教授，博士生导师，1948年生