网结构隔振特性的理论与实验研究

网结构隔振特性的理论与实验研究

裴亚鲁1,2,黄修长1,2，张志谊1,2

(1.上海交通大学振动、冲击、噪声研究所，上海200240； 2.上海交通大学机械系统与振动国家重点实验室，上海200240)

摘要：针对航天器微振动高性能隔振的特殊要求，提出一种基于网结构的新型隔振方法，对由振源-网结构-弹性边界构成的耦合系统进行了振动建模与分析。对于网结构，采用子结构导纳综合法建立其模型，获得了垂直于网面的频域振动方程；对于边界梁，采用弦-梁单向耦合，将动态张力沿垂直和水平方向分解，得到振动响应的完整描述。在此模型基础上，分析了耦合系统的振动传递特性。为验证理论的正确性，设计并搭建了网结构微振动实验台。结果表明，网结构平台具有良好的被动隔振效果，在较宽的频段内，可以实现20 dB以上的振动衰减。

关键词：隔振平台；耦合系统；子结构导纳法；振动传递

中图分类号:TB535.1文献标志码：A

基金项目：国家自然科学基金(51168021)

收稿日期：2013-09-12修改稿收到日期：2014-01-02

Theoretical and experimental study on the vibration isolation performance of a grid-structure

PEIYa-lu1,2,HUANGXiu-chang1,2,ZHANGZhi-yi1,2(1. Institute of Vibration, Shock and Noise, Shanghai Jiao Tong University, Shanghai 200240, China;2. State Key Laboratory of Mechanical System and Vibration, Shanghai Jiao Tong University, Shanghai 200240, China)

Abstract:A novel vibration isolation method using a plane grid structure was presented to meet the special demand of high-performance vibration isolation against microvibration in spacecraft. The vibration of a coupled system, which consists of vibration source, grid structure and flexible support, was modeled and analyzed. The out-plane vibration equation of the grid structure in frequency domain was obtained by using the substructure mobility synthesis principle. Based on the assumption that the coupling between string and beam is unidirecional, a complete description of the vibration of the beam was achieved by decomposing the dynamic tension force of the string in the vertical and horizontal directions. The vibration transmission characteristics were analyzed in terms of the synthesized model and an experimental platform was set up to verify the isolaion performance of the grid structure. The results show that the grid-structure is effective in vibration isolation and more than 20dB attenuation in transmission can be achieved.

Key words:vibration isolation platform; coupled system; substructure mobility approach; vibration transmission

航天器微振动是影响高精度遥感卫星指向精度和成像质量等关键性能的主要因素[1]，由于其微小性、固有性、宽频性和难控性，航天器的微振动力学环境极为复杂和特殊，分析与控制难度都很大[2]。此外，太空使用环境对振动控制系统的复杂性、可靠性、稳定性等方面都有新的严格要求，例如地面广泛使用的橡胶类隔振器，必须通过空间模拟环境试验，其材料不能有辐射不稳定组分，这就严重限制了常规材料的应用。因此，对于太空环境，必须考虑使用环境的特殊性，研究和发展新型隔振系统[3-5]。

本文研究的网结构隔振平台由振源平台、网结构和边界支承组成。网结构由相互交错的张紧弦构成，而支承结构则是由梁或板-梁组合体构成。迄今为止，有关弦的振动建模与分析方法，国内外学者已经开展了大量研究，如Liu等[6]研究了参数激励作用下两端拉紧的弹性弦线的小幅非线性振动，考虑了由于振动引起弦线长度变化而导致的非线性因素；Bank等[7-9]对钢琴弦振动做了深入研究，详细探讨了弦中的纵横耦合及共振等问题。对于弦梁耦合结构，因其在机械、建筑等领域的广泛应用，也已有大量的研究与成果，如Cheng等[10]把光纤耦合器简化成一个具有四个节点的弦梁耦合系统，建立了正弦激励下系统的振动理论模型；Michel等[11]研究了桥梁工程中的斜拉索，将索-梁耦合振动分解为沿索轴向的参数振动和垂直于轴向的强迫振动。但是，索与弦模型并不完全等效，而且这些实际工程应用多涉及大变形，因而对弦梁耦合振动的研究也多为非线性动力学研究。

本文研究网结构在微振动条件下的振动特性，特别是网结构中的脉动张力及其对边界的作用。经典弦振动振动方程没有考虑张力脉动，因为考虑张力脉动的弦振动方程是非线性的，含有张力相关的高次项，与弹性边界耦合后的振动方程更加不易求解，目前还没有一般性方法。本文旨在提出网结构振动的数学物理模型及求解方法，以揭示耦合系统的振动传递特性。

1网结构隔振平台构造

如图1所示，平台包括振源安装平台、平台支承、网结构以及弹性边界支承。网结构是隔振系统的关键组成部分，其中网线由高强度金属线交错编织而成，端部固定于金属框架，框架上有网线张力调整单元，张力及其脉动由力传感器检测。

外界激励通过振源平台作用于网结构，网结构中的张紧力随之发生变化，进而引起弹性边界的振动。通过分析振源平台与边界支承的振动响应，以及网结构的张力变化规律，可以研究网结构的隔振效果以及振动传递衰减特性。

本文首先以振源-网结构-弹性边界构成的耦合系统为研究对象，进行振动建模和传递特性分析；然后进行实验平台的搭建，测试以及实验验证。理论建模时，振源采用刚体模型，振源平台与网结构刚性连接。网结构和边界支承分别采用张紧弦和简支梁描述，耦合系统模型通过子结构导纳法建立。建模中不计及重力对系统振动的影响。

2基本理论

2.1弦的振动描述

以两端自由的张紧弦为研究对象，如图2所示。弦长l，在距离端部h处受横向简谐力Feiωt作用。

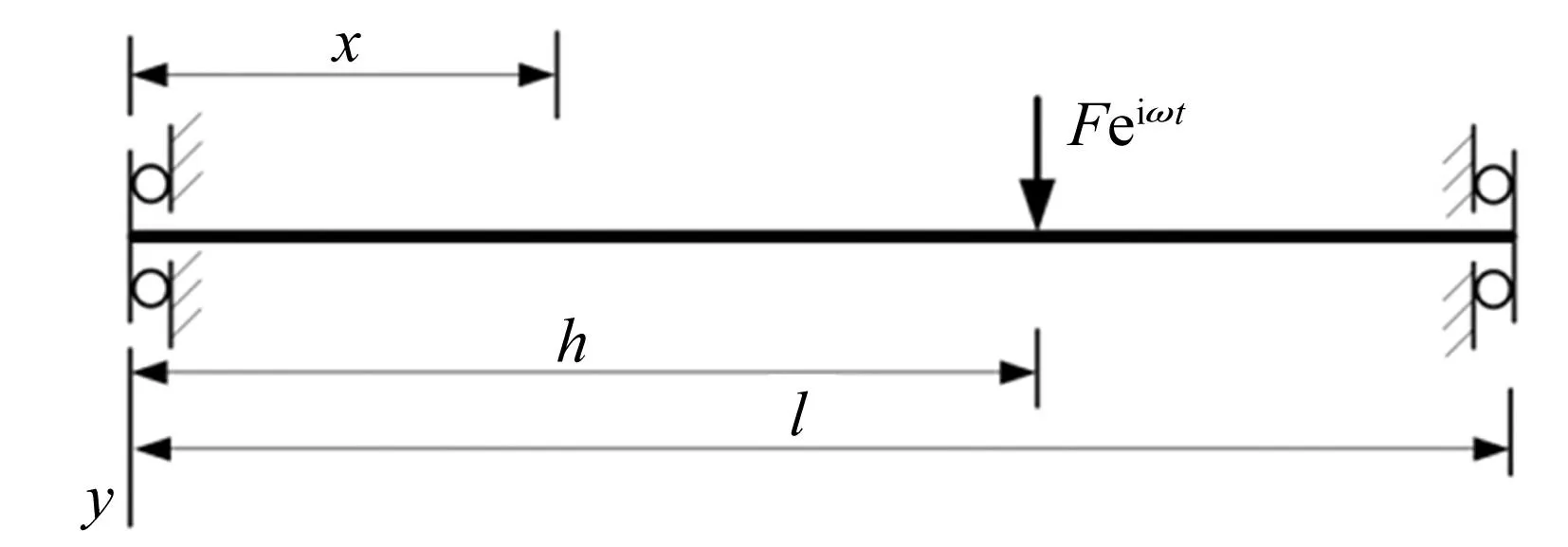
图2两端自由的张紧弦横向受力模型 Fig.2 Free-free tensioned string with a lateral force

基本假定：不计阻尼；弦只承受拉力，且在静态工作点附近的变形符合胡克定律；考虑微幅振动，不计弦的纵向振动[8]。

2.1.1弦的横向振动

弦横向振动的微分方程：

(1)

式中，μ=ρA，ρ为弦密度，A为弦横截面积，T0为弦预紧力，t为时间。

边界条件：

(2)

距离端部x与h处两点间的跨点位移导纳[12]：

(3)

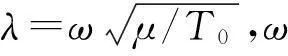
2.1.2弦内张力变化

弦的横向振动使得弦内张力发生变化，取弦段上的微元dx进行分析，如图3所示。

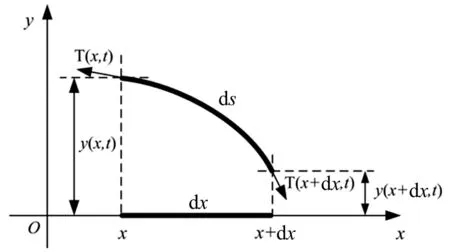
图3　弦段微元ds模型 Fig.3 Short element of the string

设微元在端部产生的横向振动位移分别为y(x,t)和y(x+dx,t)。微元长度变为ds，近似计算如下：

(ds)2≈(dx)2+[y(x+dx,t)-y(x,t)]2

(4)

由于dx无穷小，式(4)可化为：

(5)

化简上式可得：

(6)

设弦内张力T=T(x,t)，由胡克定律得[8]：

(7)

将式(6)代入式(7)，忽略高次项，得张力T的计算公式：

(8)

式中，E为弦的弹性模量。

2.2梁的理论模型

以两端简支的矩形截面梁为研究对象，如图4所示。梁长l，在距离端部a处受简谐力fsinωt作用。

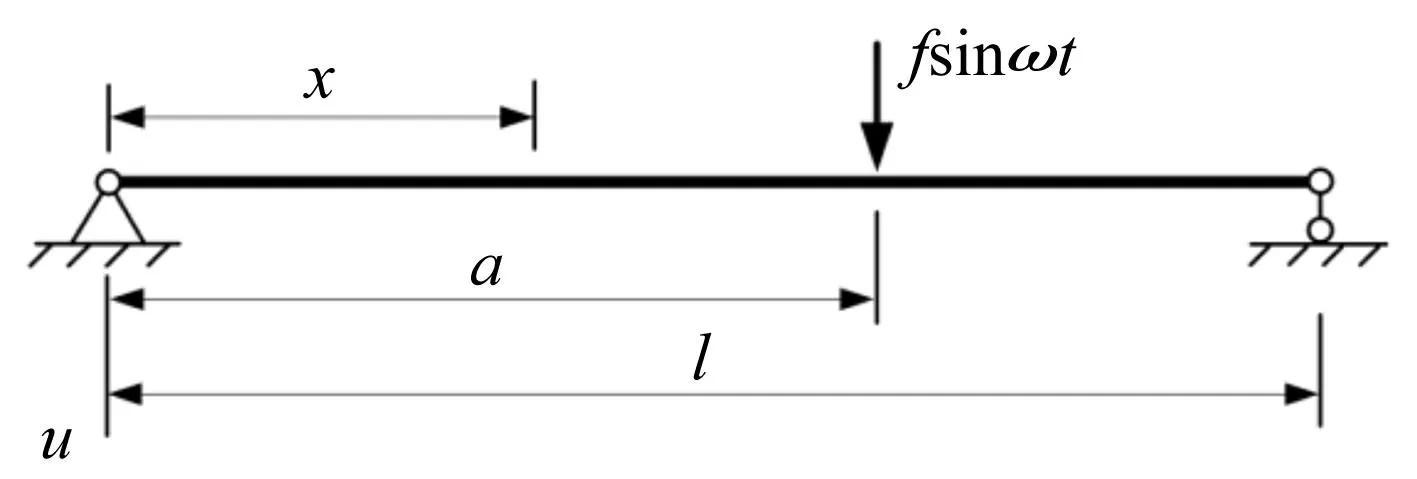
图4　两端简支梁横向受力模型 Fig.4 Simply supported beam under a lateral force

梁的横向振动微分方程：

(9)

边界条件：

(10)

固有频率:

(11)

距离端部x与a处两点间的跨点位移导纳[11]：

(12)

2.3刚体的理论模型

建立质量均匀的刚体模型，如图5所示。长宽高分别为a、b、c，坐标系O-XYZ以刚体质心为原点，各坐标轴平行于刚体棱边。

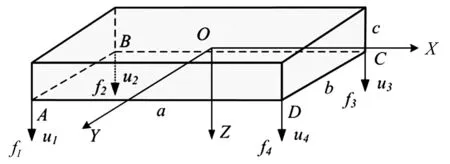
图5　刚体模型 Fig.5Rigid body model

频率为ω时，A、B、C、D处的4个节点力fi与相应节点位移ui之间的关系为[12]：

(13)

式中:

式中，m为刚体质量，Jx、Jy为转动惯量。

3刚体-网结构-边界梁耦合系统建模

耦合系统由刚体、网结构与边界梁三个子系统构成，如图6所示。网结构四根张紧弦呈“井”字交错，端部固定于简支梁上，网结构与刚体在弦交叉点处刚性连接，各连接点满足位移协调和力平衡条件。图中，P为一个弦-梁连接点，Q为距端部为x的弦上一点。

图6　刚体-网结构-边界梁耦合系统建模 Fig.6 Coupled system modeling

假定在刚体质心处施加沿Z向的简谐激励，研究耦合系统中网结构和边界梁的振动响应特性。

3.1子结构导纳法建模

主要研究网结构在网面垂向的振动传递特性。建模假定：不计梁的初始变形，忽略阻尼。

子结构导纳法是对有限个自由度耦合的两个结构进行拼装和振动分析的有效方法，在隔振系统的振动传递分析中已得到实际应用[15]。本文采用由Jetmundsen提出的机械导纳法[16]，得到两个子结构的导纳综合公式：

(14)

式中：上下标A和B表示子结构A和子结构B；j表示子结构A和子结构B的连接坐标；i表示内部坐标。

基于上述子结构导纳法，进行四次导纳综合，如图7所示。分别建立交叉弦模型、井字弦模型、弦梁耦合模型以及与刚体综合后完整的耦合系统模型。

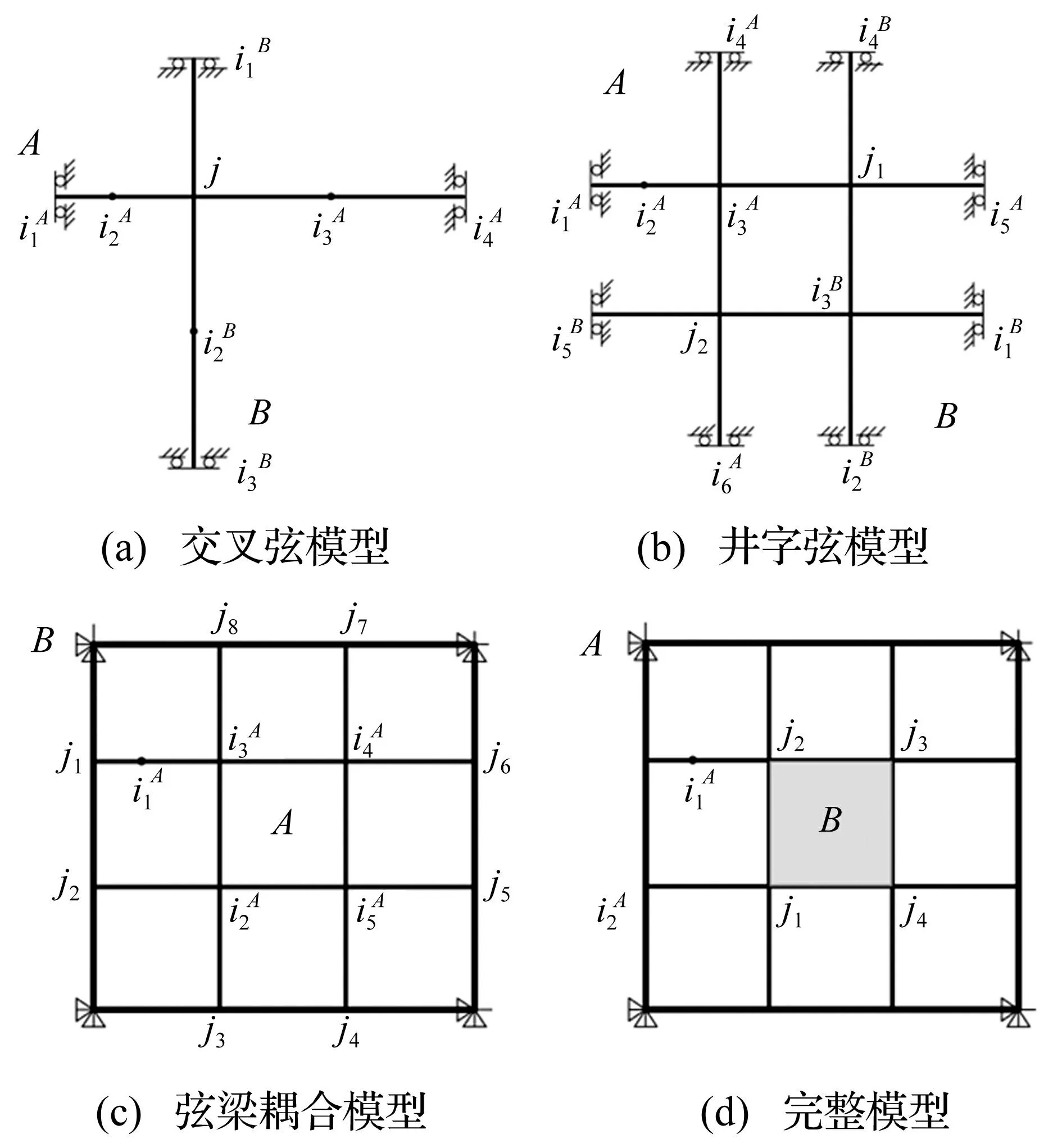
图7　耦合系统导纳综合建模 Fig.7 Mobility synthesis modeling of the coupled system

由此，即可确定组合模型在图6各点处的导纳矩阵H，以及各点激励力与位移响应的关系：

(zQzPzAzBzCzD)T=

H(fQfPfAfBfCfD)T

(15)

需要指明：①由于Q点的任意性，可以得到该弦段各点处的振动响应特性；②假设激励作用于刚体任意位置，可将其平移和旋转至质心，然后等效变换为A、B、C、D处的4个节点力，最终得到模型在各点处的频响特性；③子结构导纳法对边界梁的振动描述并不完整, 边界梁的振动是在张紧弦动态张力作用下的强迫振动，而子结构导纳法只研究了边界梁沿网面垂向的振动特性。

3.2边界梁振动的完整描述

边界梁的振动还可以通过将弦端部动态张力分解到垂直与平行于网面方向进行研究：将垂直和水平张力分量分别作用在边界梁上，然后进行振动响应的合成，即可获得梁在弦梁耦合点处总的响应特性。

将式(8)确定的弦动态张力沿垂直网面方向分解，得垂向分量：

(16)

式中，y(x,t)可由式(15)中的zQ(x,t)确定。

令式(16)中x=0，得到弦端部动态张力的垂向分量，将其作用于边界简支梁上，如图8所示。

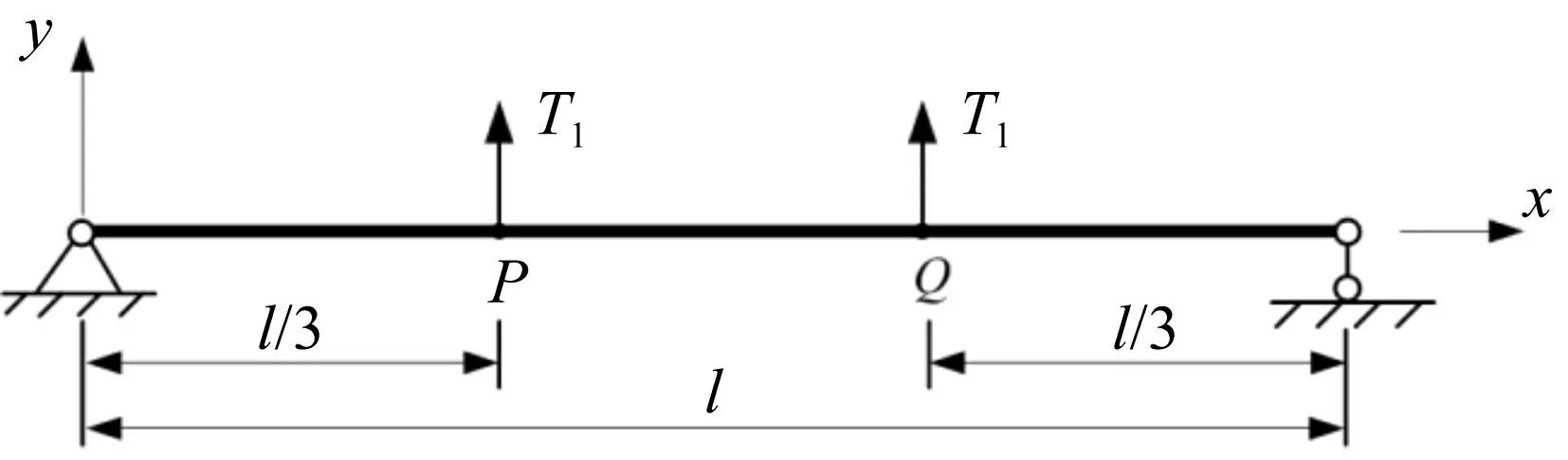
图8　边界简支梁的受力模型 Fig.8 Boundary beam under tension of the strings

在线弹性、小变形条件下，由式(12)，通过叠加法可以求得梁在弦梁耦合点P、Q处沿网面垂向的位移响应幅值：

(17)

式中，T1为由式(16)确定的动态张力幅值。

同理，得到动态张力的水平分量：

(18)

以及边界梁平行网面方向的位移响应幅值y2。将水平和垂直方向的响应进行合成，即可得到梁沿弦方向总的位移响应幅值：

(19)

通过改变激振频率ω，即可得到边界梁在弦梁耦合点处总的振动频响特性。有必要指明，这里采用的张力分解的方法是基于弦梁的单向耦合，即弦的张力变化引起梁的振动响应，但不计梁对弦振动的影响。

4算例分析

在刚体质心处施加垂向单位简谐激励力，研究耦合系统的振动传递特性，建模参数如下：

弦模型：弹性模量E=2×1011N/m2，长度l=1 m，横截面积A=10-5m2, 预紧力T0=100 N，密度ρ=7 800kg/m3；

梁模型：弹性模量E=2×1011N/m2，长度l=1 m，密度ρ=7 800 kg/m3，横截面宽、高b=h=0.05 m；

刚体模型：质量M=5 kg，长、宽a=b=1/3 m，高c=1/12 m。

4.1边界梁的频响特性

将弦端部动态张力的垂直和水平分量分别作用于边界简支梁，得到梁在弦梁耦合点处垂直和平行于网面方向的加速度频响，与刚体原点加速度频响对比，如图9所示。

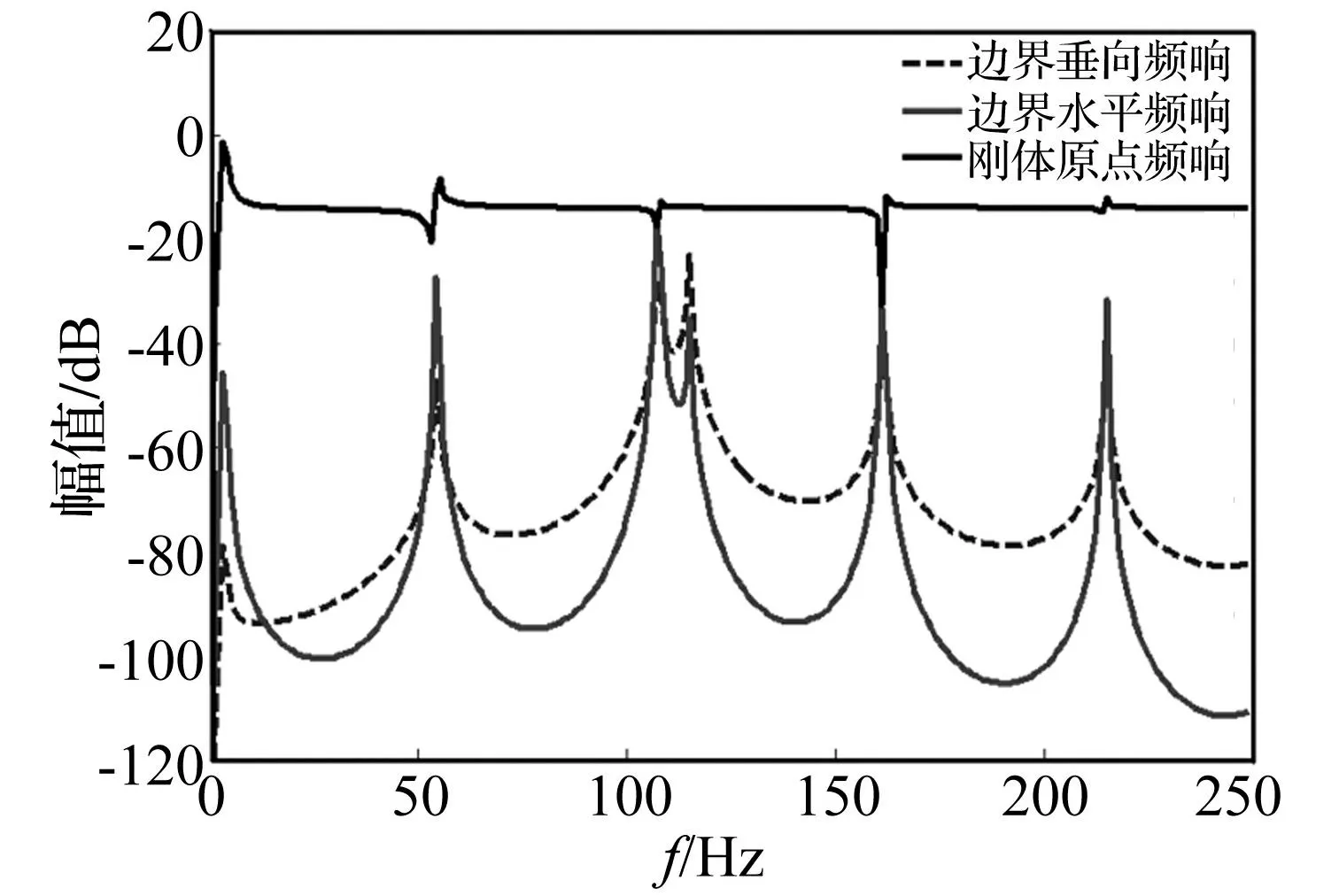
图9　边界梁的跨点加速度频响与原点频响比较图 Fig.9 Comparison of frequency responses

图9表明，网结构可以实现刚体到边界梁振动的大幅衰减；由于采用垂向激励，弦动态张力的水平分量较小，故使用等截面梁所得边界的水平振动量级也较小。

4.2力传递特性

用张紧弦对边界梁的动态张力幅值除以激励力幅值，得到耦合系统的力传递随频率的衰减，如图10所示。

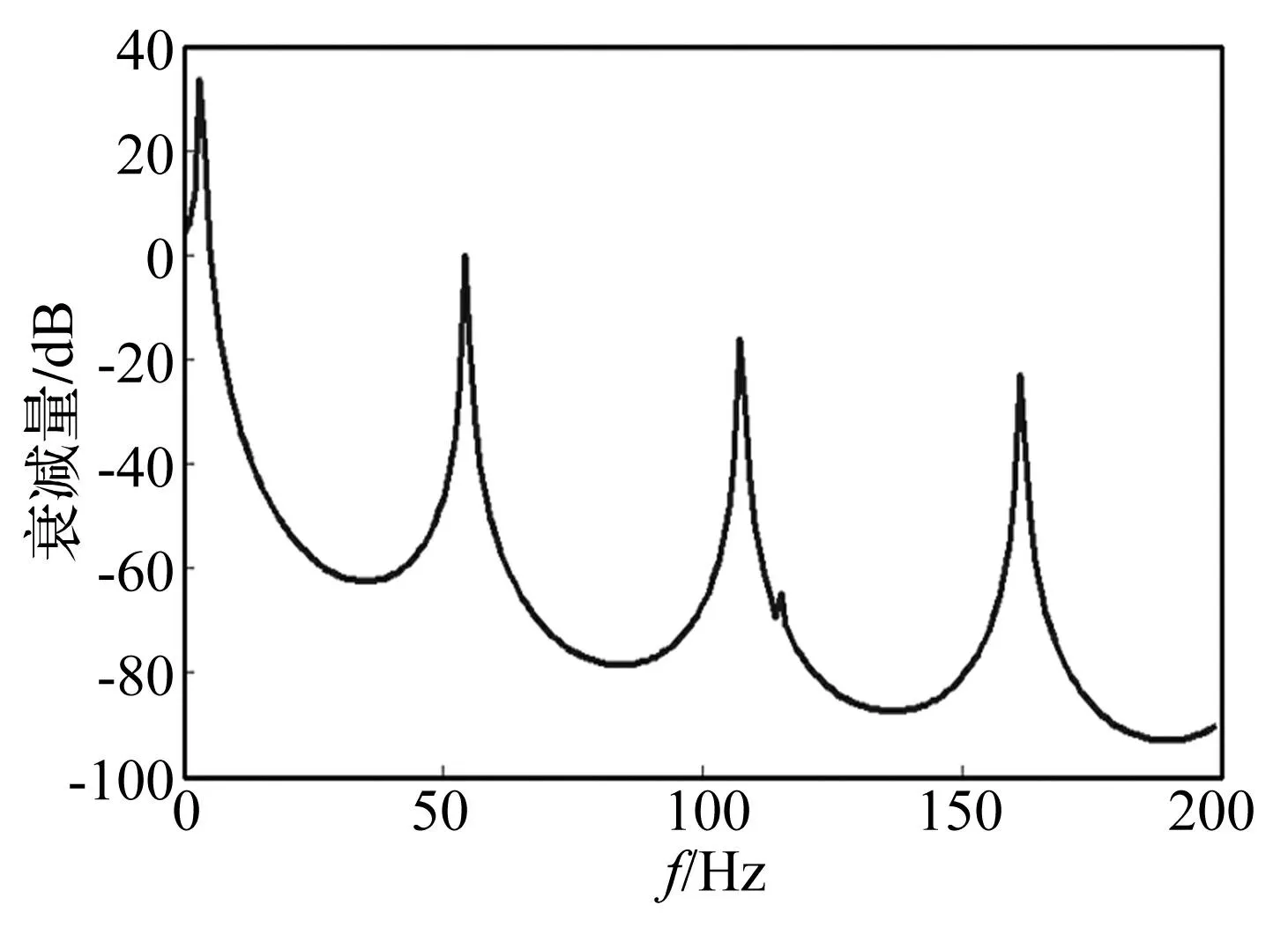
图10　力传递特性曲线 Fig.10 Attenuation of the force transmission

图10表明，力的传递除了低频段以及共振峰处衰减较小外，在其它频段都较为显著。

5实验研究

设计并搭建网结构微振动实验平台，如图11所示。平台是由相互交织张紧的钢丝绳，铝合金边界支承和上平板组成的综合系统。

图11　网结构隔振实验平台 Fig.11 The grid-structure-platform for experiment

两根钢丝绳纵横穿过侧板上的通孔，相互交叠，固定端一端放置应变式力传感器，用于检测网结构初始的静态预紧力，另一端安装有压电式的力传感器，用以检测振动传递过程中的动态张力变化。边界支承由四个铝合金侧板通过螺栓紧固连接，上平板支承于网的四个交叉点。在边界侧板与上平板上布置加速度传感器，测试其加速度响应。

实验采用力锤激励方式，得到上平板到边界侧板的频响以及力传递衰减特性。整个系统的传感器布置图如图12所示。测出各测点的响应值，信号直接进入信号采集与分析仪器。

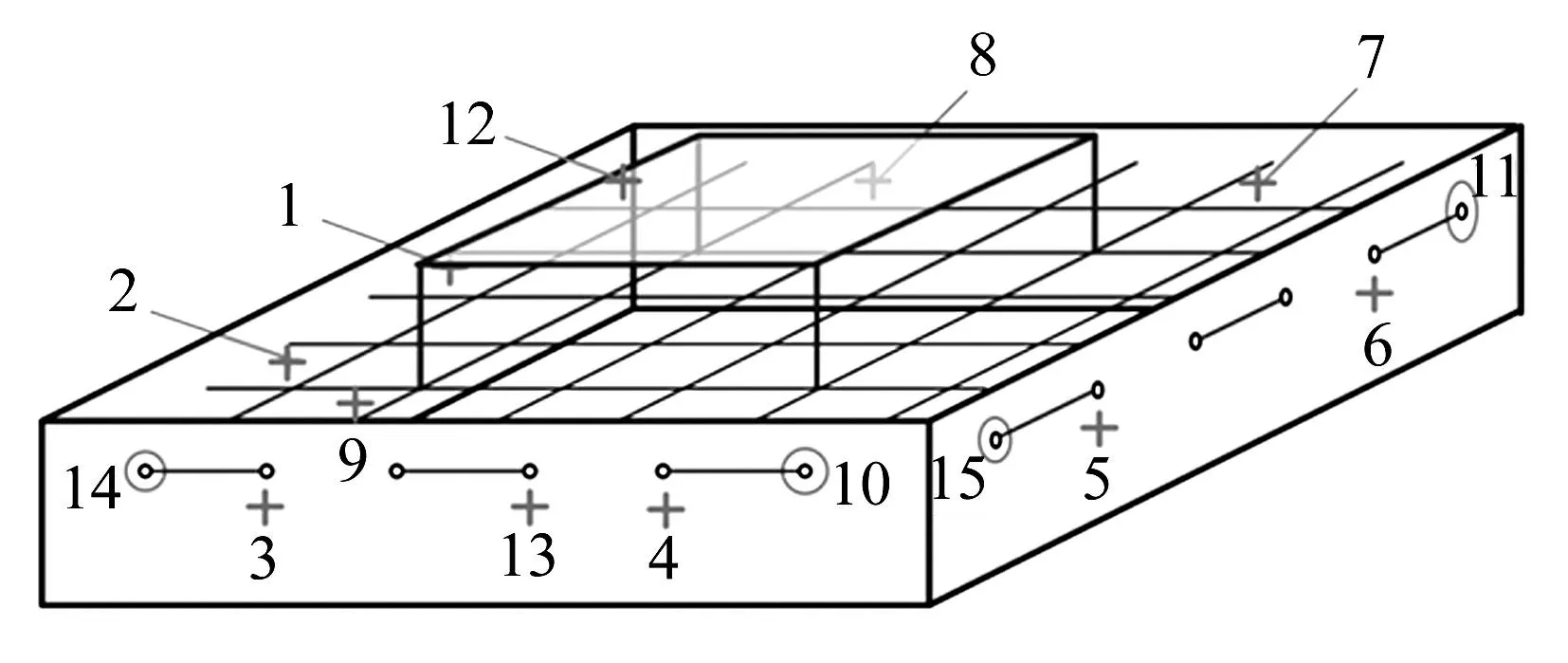
测点1-8，13—— 测试侧板的水平加速度响应； 测点9 —— 测试侧板的垂向加速度响应； 测点12 —— 测试上平板的垂向加速度响应； 测点10, 11 —— 测试钢丝绳的静态预紧力大小； 测点14,15 —— 测试钢丝绳的动态张力波动； 测点16 —— 测试力锤的冲击力信号。 图12　传感器布置图 Fig.12 Arrangement of transducers

5.1背景振动

由于网结构隔振平台的隔振对象是微振动，对实验环境要求较高，振动环境应在10-3g量级。因此，需要严格控制外界干扰，并对背景振动进行测试。

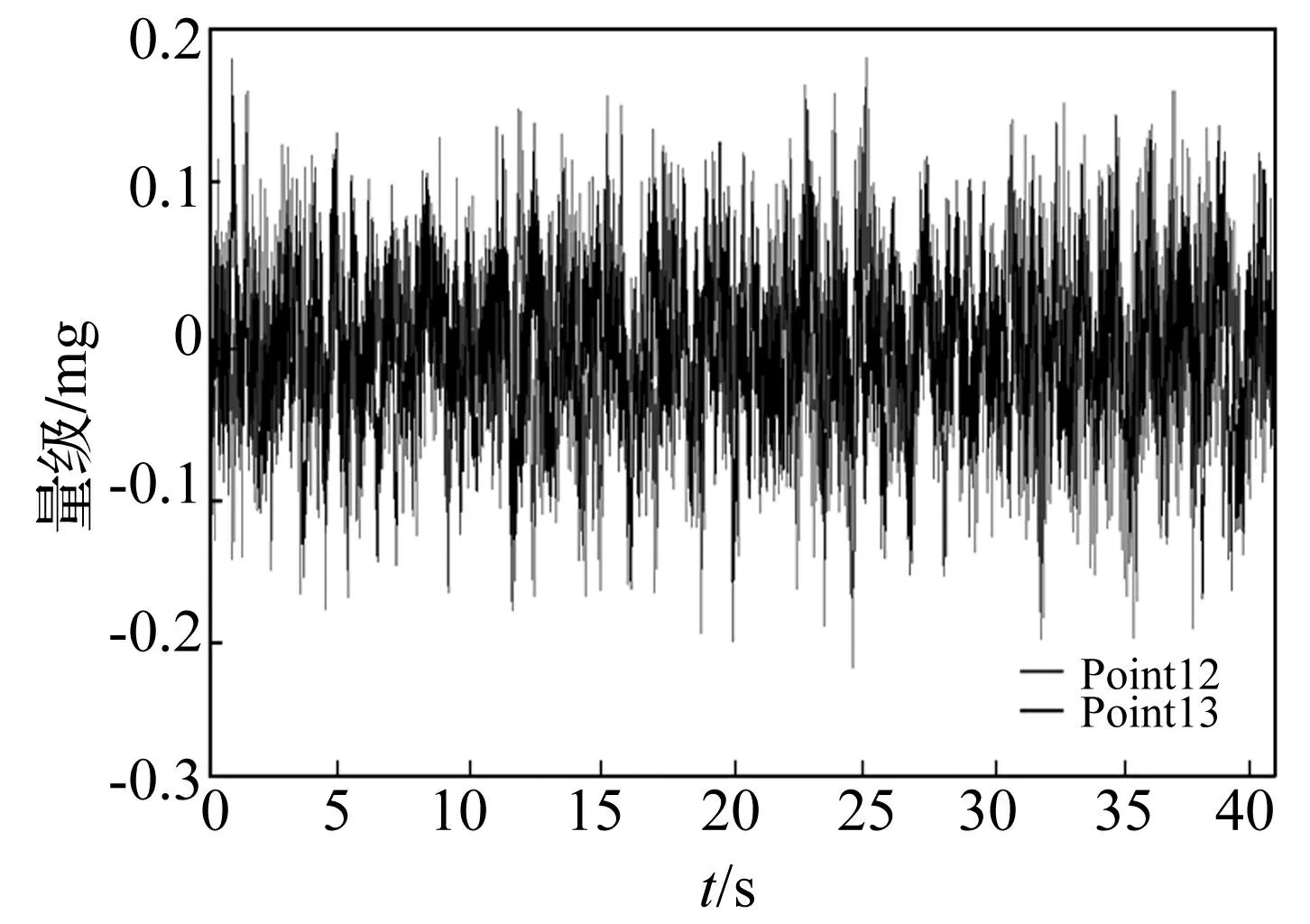
图13　背景振动 Fig.13 Background vibrations

图13是加速度传感器12和13拾取的背景振动可以喊出，上平板和边界侧板的背景振动小于0.2×10-3g，满足微振动的实验条件。

5.2频响测试

首先，由力传感器测得钢丝绳纵、横两个方向的静态预紧力，分别为59 N和67 N；然后，用力锤锤击上平板中心，测试上平板垂向以及边界侧板水平和垂直方向的振动加速度响应，得到频响特性曲线如图14所示。

图14表明，在较宽的频段内，平台在水平方向可以实现20 dB以上的振动衰减，在垂直方向则有30 dB以上的振动衰减。需要指明: ①由于采用加速度传感器，接近0Hz的测试数据并不精确。②边界支承采用板结构，垂向刚度远大于水平刚度，故垂向振动响应较小，为研究网结构本身的振动传递特性，还需要进行力的传递测试。

图14　频响特性曲线 Fig.14 Frequency response characteristics

5.3力传递测试

将力锤冲击力和由测点14、15处力传感器测得的动态张力送入信号采集仪，得到网结构面内纵、横两方向力传递衰减的特性曲线，如图15所示。

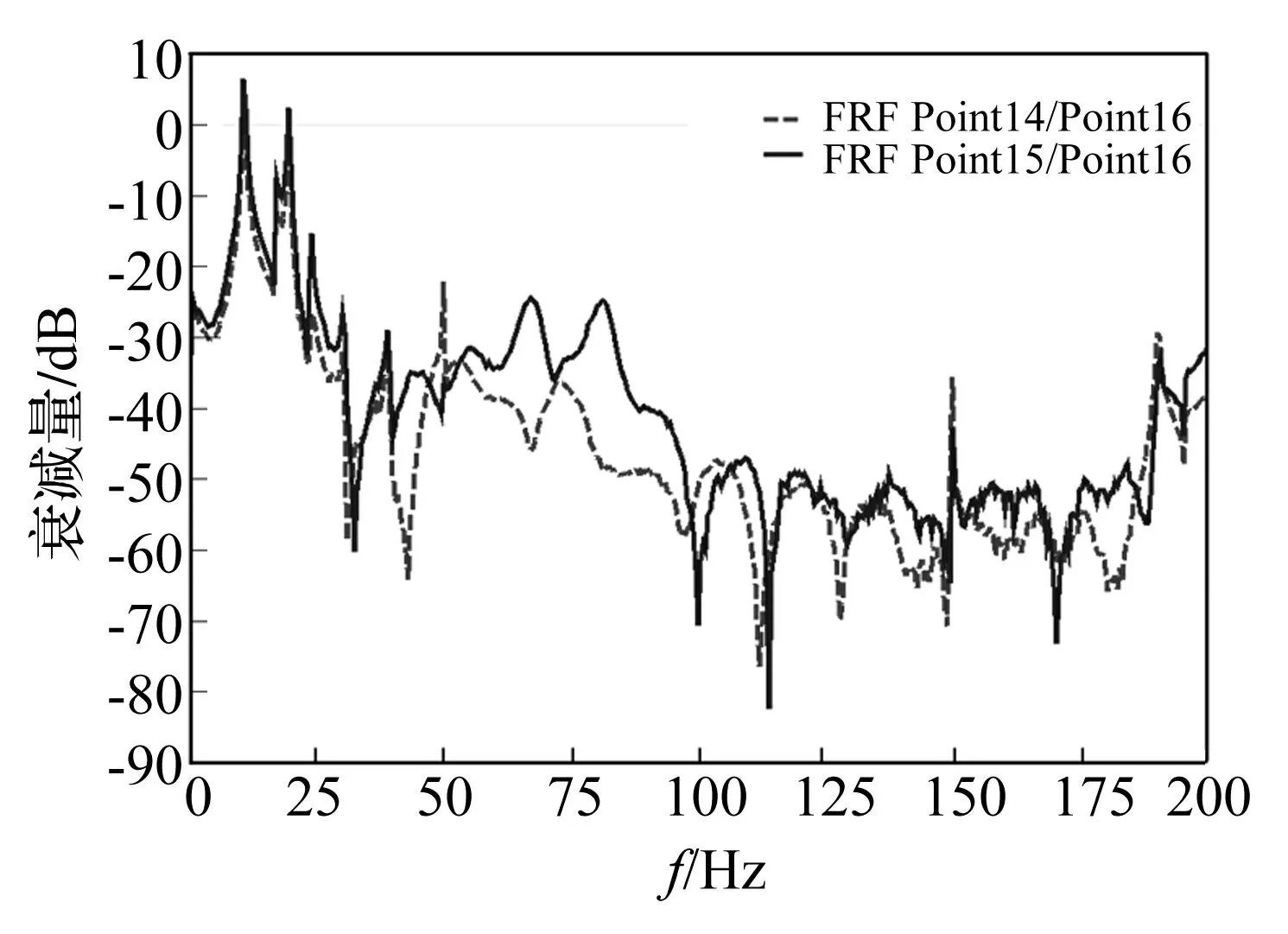
图15　实测力传递衰减曲线 Fig.15 Measured attenuation of force transmission

图15表明，网结构能够实现激励力从上平台到边界支承的大幅衰减。在0~200 Hz频段内，衰减特性良好，可达20 dB以上(除平台的两个固有频率处)。此外，纵、横方向的力传递特性基本一致，中频段的差异与两钢丝绳张力差异有关。

6结论

本文对所提出的网结构隔振平台进行了振动建模、计算分析以及实验研究，为这种轻型隔振平台的设计提供了理论基础。主要结论如下：

(1)利用子结构导纳综合法能够得到“振源-网结构-边界支承”耦合系统在各连接点处垂直于网面的加速度响应。

(2)通过张力分解的方法可以完整描述边界梁的振动，所得垂向振动分量与子结构导纳法的结果一致，而且该方法能够给出梁平行于网面方向的加速度响应。

(3)网结构隔振平台具有良好的被动隔振效果。实验结果显示，在0~200 Hz频段内，水平、垂向都能够实现较大的振动衰减；与低频段相比， 中高频段有更好

的力传递衰减特性；对于力的衰减特性，理论预测与实验结果的趋势一致。

参考文献

[1]庞世伟, 杨雷, 曲广吉. 高精度航天器微振动建模与评估技术最近进展[J]. 强度与环境, 2007, 34(6)：1-9.

PANG Shi-wei, YANG LEI, QU Guang-ji. New development of micro-vibration integrated modeling and assessment technology for high performance spacecraft[J]. Structure & Environment Engineering, 2007, 34(6)：1-9.

[2]马兴瑞，于登云，韩增尧, 等. 星箭力学环境分析与试验技术研究进展[J]. 宇航学报, 2006, 27(3)：323-331.

MA Xing-rui, YU Deng-yun, HAN Zeng-yao, et al. Research evolution on the satelite-rocket mechanical environment analysis & test technology[J]. Journal of Astronautics, 2006, 27(3)：323-331.

[3]Bronowicki A J. Vibration isolator for large space telescopes[J]. Journal of Spacecraft & Rockets, 2006, 43(1)：45-53.

[4]Rittweger A, Albus J, Hornung E. Passive damping devices for aerospace structures[J]. Acta Astronautica, 2002, 50: 597-608.

[5]Foshage J, Davis T, Sullivan J. Hybrid active/passive actuator for spacecraft vibration isolation suppression[C]// Actuator Technology and Applications: Proceedings of the Society of Photo Optical Instrumentation Engineers, 1996, 2865, 323-335.

[6]Liu I S, Rincon M A. Effect of moving boundaries on the vibrating elastic string[J]. Applied Numerical Mathematics, 2003, 47(1)：159-172.

[7]Bank B, Sujbert L. Modeling the longitudinal vibration of piano strings[C]// Stockholm Music Acoust, Stockholm, Sweden, 2003：143-146.

[8]Bank B, Sujbert L. A piano model including longitudinal string vibrations[C]// Digital Audio Effects, Naples, Italy, 2004：89-94.

[9]Bank B. Accurate and efficient modeling of beating and two stage decay for string instrument synthesis[C]// MOSART Workshop on Current Research Directions in Computer Music, Barcelona, Spain, 2001：134-137.

[10]Cheng G, Zu J W. Dynamic analysis of an optical fiber coupler in telecommunications[J]. Journal of Sound and Vibration, 2003, 268：15-31.

[11]Michel V. Cable vibration in cable-stayed bridges[J]. Bridge Dynamic, 1998：213-233.

[12]Bishop R E D, Johnson D C. The mechanics of vibration[M]. New York: Cambridge University Press, 1960：172-185.

[13]Rao S. Mechanical vibration[M]. Fourth Edition. New Jersey：Pearson Prentice Hall, 2004：439-447.

[14]Louis N, Janet D. Analytical mechanics[M]. New York: Cambridge University Press, 1998.

[15]Liu W, Ewins D J. Substructure synthesis via elastic media[J]. Journal of Sound and Vibration, 2002, 257(2)：361-379.

[16]Jetmundsen B, Bielawa R, Flanelly W. Generalized frequency domain substructure synthesis[J]. Journal of the American Helicopter Society, 1988, 33(1)：55-65.

第一作者宋志刚男，博士，教授，1974年7月生