小学一年级数感不良儿童的筛查与动态干预*

张丽锦 毕 远 梁 熠 刘敏红

(1陕西师范大学心理学院,西安 710062) (2宁夏大学,银川 750021)

1 引言

数学学习困难(math learning difficulty,MLD,简称数学困难,MD)表现为儿童的阅读与拼写能力正常,但算术能力显著低于其智龄水平。作为一个会长期阻碍儿童从正常教学中获益的问题,与之相关的筛查、干预和预防等领域长期受到教育学、心理学研究者和教育实践工作者的普遍关注。目前国内对数学困难的诊断和甄别大多使用的是能力—成绩差异模型(ability-achievement discrepancy models)(见毕远,张丽锦,2014),即基于学习困难是智力与学习成绩不匹配的基本构念,通过控制阅读能力来考查智力与数学成绩的匹配情况。但是,由于小学低年级儿童的数学成绩普遍较高,数学成绩并不能很好地反映数学能力,若要可靠地鉴别数学困难儿童,至少要到小学四年级数学成绩相对稳定且出现显著分化以后。实际上,在小学一、二年级甚至幼儿时期,有些儿童就已经表现出数学学习上的困难和障碍,需要及时甄别并给予训练和辅导。根据DSM-Ⅴ的诊断标准,学习困难出现在学龄期,当对儿童学业能力的要求超过他们有限的能力时(例如,限时测验、在规定时间内完成阅读或撰写一定长度和复杂度的文章,超负荷的学习负担等),学习困难才会明显表现出来(American Psychiatric Association,2013)。所以,对于学前儿童使用“数学学习困难”应当谨慎,对于小学低年级儿童,出于学习成绩普遍偏高的考虑也要谨慎。国外研究者通常使用的概念是“数学困难风险儿童”(children at risk for mathematics difficulties),本研究用的是“数感不良儿童”,为的是准确使用概念和诊断标准。

数感(number sense)是关于数字间关联的意识和直觉能力(Malofeeva,Day,Saco,Young,&Ciancio,2004),它从幼儿早期开始显现并一直发展着,直到小学中年级成熟。对幼儿和小学低年级儿童来讲,数感的核心成分包括对小数量(小于3或5——视不同任务而定)的快速直觉、数型识别、数量比较、数量估计、数数以及执行简单的数量转换等(见Berch,2005;Case,1998)。这些基本数感能力是独立于语言与空间知识和一般记忆能力的特定的认知功能(Gelman &Butterworth,2005;Landerl,Bevan,&Butterworth,2004)。数感的这种对数量和大小的直觉能力可能是先天的并且是早期数学学习的基础(Geary,2006),同时它也与儿童早期数概念的教育和经验有关(Case &Griffin,1990),可以通过学习和训练得到改善。也就是说,数感不仅涉及非语言数字系统,也与受经验和学习影响的语言数字系统有关(Geary,1995;Levine,Jordan,&Huttenlocher,1992)。幼儿早期就表现出来的对小数量的识别、比较和操作上的不同敏感度和差异体现了不同的数感水平。如果儿童不能理解数量之间的关系组合,将不利于算术事实(arithmetic fact)的获取和提取。

与受到的关注不相称的是,对于数感,目前还没有一个公认的定义。数感被认为是一个“好识别,难定义”(Case,1998)的概念。尽管研究者对数感的组成各持己见,比如,Berch (2005)曾汇总研究者对数感成分的划分,发现多达 30余种;但如前所述,研究者们对数感核心成分的认识还是比较一致的(见 Berch,2005;Case,1998)。虽然与数感有关的概念和理论问题尚未解决,但能够指导测量与干预的数感模型已经构建而成。Jordan及其同事(Jordan,Kaplan,Oláh,&Locuniak,2006)基于以往研究和自己的发现,提出了儿童数感的“五成分能力结构”理论模型。这五成分包括：数数(counting)、数知识(number knowledge)、数量转换(number transformation)、数量估计(number estimation)和数型(number patterns)。五成分数感结构在发展上有先后顺序,每一阶段数感的发展以前一阶段各成分能力的获得为基础。五成分的这种逐级支撑与依次获得的关系反映出儿童数感发展的轨迹和阶段,为数感的细化研究、测量评估和干预训练提供了理论指导。尽管Jordan的数感五成分理论及其测验未必详尽涵盖了被研究确认的和与小学数学课程有关的数学认知内容,但对基本的数学能力都有涉及,而且可以排除是对基本认知能力(如,一般工作记忆)的考查。五成分模型强调数感是对儿童关于数、数量关系和数量操作的直觉,对儿童日后更高层级(higher-order)的数学思维(如数量操作与数量程序中的流畅性与灵活性)非常重要,所以数感对数学成绩有显著的预测作用。研究发现,幼儿园和小学低年级儿童的数感水平可以预测其更高年级的数学成绩(Chard et al.,2005;Dyson,Jordan,&Glutting,2013;Geary,2011;Jordan,Glutting,Dyson,Hassinger-Das,&Irwin,2012)。幼儿园时的数感表现可以解释一年级数学成绩66%的变异,而家庭背景、性别、年龄的解释都明显低于数感(Jordan,Hanich,&Kaplan,2003b);一年级上学期的数感成绩,可以很好地预测一年级下学期和三年级的数学成绩,且预测力不随时间衰减(Jordan,Glutting,&Ramineni,2010)。需要特别说明的是,数感测验和数学成绩测验在内容和形式上是有所不同的,一般来讲数感测验在内容上要比同一时期的数学测验所涉及的数字范围更广,在题型设计上也要考虑对被试的相对新异性,尽量使儿童无法直接依靠已经学到的算术知识或数字事实解决问题。

数感被认为是人的一种基本数学素养,是建立明确的数概念和有效计算的基础,是在数学与现实问题之间建立联系的桥梁。与数学认知发展不同,数感能力强调儿童对数字的直觉或感觉,以及主动运用这种直觉“以灵活而有创造性的方式”(Sowder,1992)解决新的数学问题。大量研究证实,数感作为鉴别数学学习困难强有力的预测指标发挥着重要的作用,儿童早期的数感不良极有可能发展成为数学困难(Anghileri,2000/2007;Chard et al.,2005;Fuchs et al.,2013;Gersten,Jordan,&Flojo,2005;Jordan et al.,2010;Locuniak &Jordan,2008;Mazzocco&Thompson,2005;Seethaler &Fuchs,2010)。同时,数感也被认为是预防数学困难的有效干预内容,这样针对数感的干预就有可能降低儿童日后出现数学困难的程度和可能性。

尽管对年幼儿童的数学困难进行诊断需要谨慎,但筛查和评鉴潜在数学困难风险儿童,或者说甄别数感不良儿童却是可行的。一是因为数感是早期发展的,对学前及小学低年级数学困难风险儿童的甄别不适合采用年级水平离差法时,数感测验不失为一个合适的选择;二是因为数感测量涉及到了多种数学加工成分,可以相对广泛地说明数学困难的多种表现。从教学实践角度来说,数感鉴别是以及早补充教学、降低风险为目的,意图对存在潜在数学困难风险的儿童进行筛查以便干预,而非提前对低年级儿童作“数学学习困难”的诊断,这既避免了错误鉴别的风险和标签效应,又满足了早期预防干预教学的需要。

检验一个数感测验反映个体数学能力的程度,可以看它与数学成绩的关联程度,也可以看它对数学困难的预测程度。此外,对于小学低年级来讲,还有一个非常可靠的指标,即计算流畅性。计算流畅性(calculation fluency或computational fluency)是指快速、准确、轻松地进行基本运算并灵活应用的能力(Kilpatrick,Swafford,&Findell,2001),是解决数学问题的重要能力。计算流畅性是低年级数学学习的特点,且与核心计算原理的基础知识相互促进,对数学学习的很多方面(从解决简单的整数问题到计算分数、小数、百分数,再到代数方程、甚至基本的几何问题)都有促进作用(Jordan,Glutting,&Ramineni,2008)。有研究发现,数学能力和计算流畅性之间的关系非常稳定,且较少受其他能力的影响(Locuniak &Jordan,2008)。

数感不良能够导致儿童在算术事实提取上的困难;而良好的数感则可以加强儿童对基本算术事实的表征(Geary &Hoard,2005;Jordan,Levine,&Huttenlocher,1994)。而算术事实是指已经转化为陈述性知识的数量转换关系(如,4 + 3=7),其特点是在解决数学问题时能够快速、轻松、准确地进行提取(Hasselbring,Goin,&Bransford,1988),即不用计算直接从记忆中获取准确答案(但并非是仅靠死记硬背积累算术事实),这显然和计算流畅性密切相关。研究发现,有逻辑意义的而非死记硬背的练习对实现流畅性非常重要(Geary et al.,2008)。可见,数感和计算流畅性之间的关系相当密切,计算流畅性也如数感一样对数学成绩和数学困难倾向有良好的预测作用。提高儿童的计算流畅性有助于他们在更高等级的数学问题上获得成功(McNeil,Fyfe,&Dunwiddie,2015)。研究主张,计算流畅性的前提性基础能力包括数感、记忆广度、阅读/语言能力和空间能力(Locuniak &Jordan,2008),作为一个外显的可操作的测量指标,计算流畅性得以发展依赖于有直觉特性的数感的发展和那些基本能力的发展。数感既然作为计算流畅性的基本要素,它的不良发展必然会导致儿童在计算方面的缺陷,并容易导致数学困难(Gersten et al.,2005;Mazzocco &Thompson,2005)。多项研究证实,数学困难儿童在解决数学问题中的一个显著表现是计算流畅性不足(Bryant,2005;Locuniak &Jordan,2008)。无论数学困难儿童的阅读能力如何,在解决一位数加法问题时,其速度和准确性方面都有缺陷,而速度和准确性对数学能力至关重要(Barnes et al.,2006;Carr &Alexeev,2011)。他们在限时计算任务上的成绩都明显不及数学正常儿童(Hanich,Jordan,Kaplan,&Dick,2001;Jordan &Hanich,2003;Jordan,Hanich,&Kaplan,2003a;Jordan &Montani,1997),从记忆中提取算术事实也表现出明显的困难(e.g.,Geary,Hoard,Nugent,&Baliey,2012)。尽管他们中的大部分在计数程序的技能使用上能赶上正常同伴,但提取算术事实的困难却一直存在(Geary et al.,2012;Jordan et al.,2003b)。

从测量的角度来看,数感是早期发展的,所以建立个体早期的评估系统既可行又有意义。对于计算流畅性来讲,即使是小学低年级儿童,考查和甄别他们在计算方面是否快速准确也是容易操作的。需要说明的是,计算流畅性可以评估小学低年级儿童的数学能力,但它并不能作为诊断和筛查量表来使用。我们前面提到,数学困难的表现有多种,而计算流畅性只是其中相对更核心的一个特征,就像心理数线与儿童的数学能力、数学成绩有很强的相关,且可以预测数学成绩一样(Booth &Siegler,2008) (心理数线与计算流畅性之间也有很强的相关)。这样,与数学能力有很高相关的数感成分当然不止流畅性和数线,它们只是良好的预测指标之一,并不能广泛地代表数学认知的能力范畴。而依据五成分理论编制的数感测验,包含了数感的多种成分,会比任何单一成分的数学能力测验更适合。

尽管国外已有比较成熟的数感测验工具,但是受家庭和学校教育因素,以及亚洲语言和英语语言数词不同的影响,东西方儿童早期的数感发展水平存在较大差异(Chan,2014;Geary,Bow-Thomas,Liu,&Siegler,1996;Rodic et al.,2015),在精确数字估计方面更是如此(周广东,莫雷,温红博,2009)。就国内情况来看,直接测量数感和与数感相关成分的测验多半是针对幼儿的。由于数感五成分的难度阶梯和逐级发展的关系,对幼儿期的数感评估会涉及不到数感的高级成分,比如,周欣及其同事开发的“3～6岁儿童学习和发展指南(草案)：认知领域发展水平测查工具(R)”(周欣,黄瑾,赵振国,杨宗华,2009),涉及的是数数策略、数量守恒和估算等数感的中、低级成分(当然,该研究使用的不是“数感”的概念)。赵振国对幼儿数感的研究使用的是改编国外测验项目的测查工具,涉及数数、数知识、数量转换3个成分(赵振国,2008)。研究发现,待明确鉴别某儿童有数学困难后再施以补救教学和特殊教育,其效果并不理想(Chard et al.,2005)。因此,若要构建涵盖五成分的且具有有效预测性的数感测验,以实现对有潜在数学困难风险儿童的及早鉴别并进行针对性干预,小学一年级儿童是比较理想的研究对象。而且考虑到我国非标准化的幼儿园教育(数感不良的高发群体——低社会经济地位家庭儿童早期的数学教育参差不齐),小学一年级作为义务教育的起点,也是一个合适的测量与干预点。

本研究的目的首先是编制一套能够对小学低年级儿童的数感水平进行评估的测验,以了解儿童数感发展的水平并筛选出数感不良儿童;其次,将探查经过对数感重要成分——数量转换和数量估计的干预后,数感不良儿童数感水平的提升情况,且这一进步是否也体现在计算流畅性上。也就是说,本研究除了在考查数感和计算流畅性密切关系的基础上,进一步探究二者中的哪一方对另一方具有预测作用之外,还将探查对具有核心意义的数量转换(包括数字组合)和数量估计的学习对小学低年级数感不良儿童的数感和计算流畅性的促进作用。Locuniak和Jordan (2008)曾对198名幼儿园儿童的数感和计算流畅性进行回归分析,发现数感中的数知识和数量组合(number combination)对幼儿园儿童计算流畅性的贡献最大,数知识每提高 1分,计算流畅性增加0.86;数量组合每提高1分,计算流畅性增加0.76。建立有效的评估方法可以发现低年级儿童的数感不足,以便于及时采取补救措施;考查何种内容的干预有助于促进儿童数感的发展,是对有效干预的考量。对于小学一年级儿童来讲,数知识已是较容易的数感成分,而有一定难度且较为核心的数量转换和数量估计可能更有助于数感不良儿童数学能力的发展与促进。

2 研究 1 “儿童数感发展测验(一年级用)”的编制

拟编制符合心理测量学标准的“儿童数感发展测验(一年级用)”,以实现识别和筛查数感不良儿童的目的。

2.1 被试

以银川市3所普通小学(西夏区九小、西夏区十小和逸夫小学)一年级儿童202人(女生95人)为被试,年龄范围在 6.12～8.61 岁,

M

±

SD

=6.43±0.65。

2.2 工具

自编“儿童数感发展测验(一年级用)”。

2.3 程序

项目构成

数感测验初始项目的形成一方面借鉴国外相关测验(Griffin,Case,&Siegler,1994;Jordan et al.,2008;Malofeeva et al.,2004)的框架和测题内容及形式;另一方面考虑到我国小学数学课程标准和教学内容,并结合小学一年级学生的认知特点,形成了56个初始项目,涵盖了数感的5个成分：①

数数

考查儿童对数数原则、基数、序数的掌握,以及依靠所掌握的基数、序数原则来解决数数问题的高级数数能力,这样可以避免明显的天花板效应;②

数知识

考查儿童区分不同数量、识别相同数量、进行数量比较的能力;③

数量转换

包含故事问题和言语计算问题,考查儿童通过加、减改变数量的计算能力;④

数量估计

考查儿童近似估计数量大小的能力;⑤

数型

考查儿童的模仿和扩充数型、识别数量间关系的能力。

正式测验的形成

第一步,确定命题双向细目表,形成数感初始测验;第二步,对 202名被试进行初测,进行难度和区分度分析,保留 46个项目;第三步,将这些项目按照“数数−数知识−数量转换−数量估计−数型”的从易到难的顺序进行编排,形成正式测验——“儿童数感发展测验 1(一年级用)”;最后,参照该测验试题的难易度和形式编制数感测验的 3个复本测验,分别命名为“儿童数感发展测验 2/3/4”。

重测

对其中89名被试在1周后进行重测。

2.4 结果

2.4.1 以命题双向细目表确定测验的内容效度

首先在数感五成分框架下构建包含 4级目标(识记、理解、应用、分析综合)的双向细目表,请10位一年级数学教师进行评定。结合编制的文字材料事先给教师讲解数感五成分的含义及试题形式,要求教师对照项目的试题卷(试卷中每道题目旁边均标明该题欲达到的上述4级目标之一),在5等级量表(1=“完全不匹配”,5=“完全匹配”)上逐项打分,评定所测内容目标与欲测内容目标的一致性。计算教师打分的平均数,结果有 4个项目平均得分低于 3,即不能很好地反映欲测内容,予以删除,保留匹配良好(平均分在3.4～4.5之间)的52个项目(见表1)。

2.4.2 项目分析

首先计算各项目的难度值(见表2),然后对各项目的得分进行高低排序,取上、下两端各27%的被试为高、低分组,进行差异性检验。结果发现,有6个项目的高、低分组间差异不显著,予以删除。项目25尽管高、低分组差异不显著,但该项目是对一张纸上的几何图形进行数量估计,其数量分别是有难度梯度的几个、10几个、20几个、30几个和40几个,25题因数量少而估计得非常准确。考虑到该项目对考查数感的意义和在数量估计题型难度梯度中的作用,所以予以保留。其余45个项目的

t

检验差异显著,区分度良好。最后保留的46个项目中,数数 6 个(T1～T6),数知识 8 个(T7～T14),数量转换 7个(T15～T17的 3个项目是故事问题,T18～T21的 4个项目是言语计算问题),数量估计16 个(T22～T29 和T39～T46),数型 9 个(T30～T38)。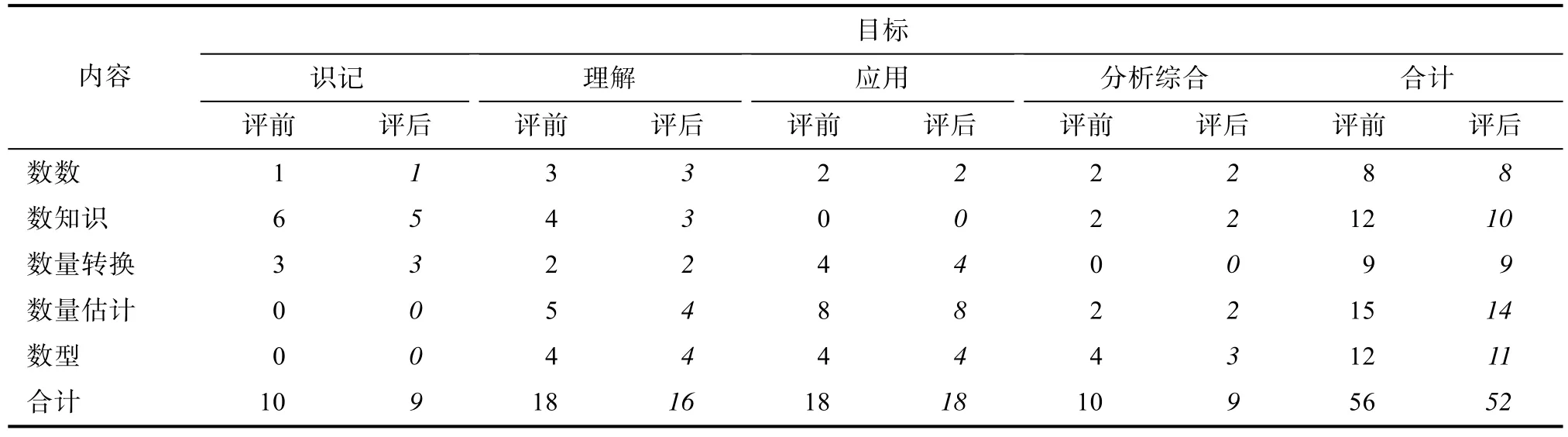

表1 “儿童数感发展测验(一年级用)”命题细目表项目评定筛选结果

表2 “儿童数感发展测验(一年级用)”各项目难度和区分度(N=202)

表3 “儿童数感发展测验”分维度信度和复本信度(n=87)

2.4.3 信度分析

本数感发展测验各维度的 Cronbach α系数均在0.70以上(

p

s＜0.05),总测验Cronbach α系数为0.90。87名被试(2人因迟到未进行重测)的重测信度为0.88。各平行测验之间的复本信度均在0.9以上(

p

s＜0.01) (见表3)。

2.4.4 效标关联效度分析

以期中和期末两次数学成绩的平均分作为效标考查测验的效标关联效度,发现数学成绩与测验各维度均呈显著的正相关(见表4),表明该测验效标关联效度良好。

3 研究2 对数感不良儿童的动态干预

研究2旨在构建促进儿童数感和计算流畅性发展的易操作、可推广的干预模式,以提高数感不良儿童的水平。研究过程为：对筛选出的数感不良儿童实施“前测−干预−后测”的动态测验方案,考查干预前、后儿童数感和计算流畅性的进步,并进一步考查二者的作用关系。

表4 数学成绩与“儿童数感发展测验(一年级用)”的相关(N=202)

3.1 被试

基于数感水平与家庭社会经济地位的相关关系(Codding,Chan-Iannetta,George,Ferreira,&Volpe,2011;Jordan et al.,2006;Malofeeva et al.,2004;Ramani,Siegler,&Hitti,2012),为了得到足够的数感不良儿童样本,从银川市城乡结合部2所新移民小学(兴泾镇回民三小、镇北堡奕龙希望小学)选取 268名一年级儿童为被试,年龄在 5.13～8.25 岁之间,

M

±

SD

=6.05±0.76。

3.2 材料

3.2.1 儿童数感发展测验(一年级用)

答对一题计1分,答错或不答计0分,满分46分。

3.2.2 一般言语与记忆能力测验

采用陈国鹏等人修订的麦卡锡幼儿智能量表(中国修订版)的言语分量表和记忆分量表(陈国鹏,李丹,1994)衡量被试的一般语言能力和短时记忆能力。

3.2.3 数集测验

以Geary等人(Geary,Bailey,&Hoard,2009)的数集测验(Number Sets Test)测量儿童的计算流畅性,该测验可以简单方便地测查儿童识别数字组合的准确性和流畅性。Geary等人(Geary et al.,2009)报告的4种计分类型的Cronbach α系数分别为——击中：0.88;误报：0.90;漏报：0.70;正确拒绝：0.85。其中击中率 + 漏报率=100%,误报率 + 正确拒绝率=100%。目标数字分别为5和9,本研究任务是：要求被试在60s (目标数字为5)或90s (目标数字为 9)的时间内,尽可能又快又准地圈出两/三个物体、两/三个数字、或者数字与物体相加等于 5或9的项目。计分标准：若相加等于目标数字时,被试圈上,则“击中”计 1分;若漏圈,则“漏报”计 1分。若相加不等于目标数字时,被试圈上,则“误报”计1分;没有圈上,则“正确拒绝”计1分。击中和误报的满分均为72分。

3.3 程序

实验程序分为3个阶段：

(1)前测阶段

对所有被试(268人)施测“儿童数感发展测验(一年级用)”“计算流畅性测验”和“麦卡锡幼儿智能量表”的言语和记忆分量表,筛选出数感测验得分处于下30% (15分),且言语分量表和记忆分量表达到常模水平(麦卡锡言语分量表5岁3个月到8岁6个月儿童的常模分数是 54～76,记忆分量表是38～55。本研究5.13～8.25岁被试的言语分量表分数是52～72,记忆分量表分数为 35～53)的数感不良儿童56人(排除智力落后)确定为数感发展不良组,再随机分为干预组29人(女13人)、控制组27人(女13人)。从余下的212名被试(排除智力落后,数感测验在16分以上)中随机抽取40名(女22人)作为正常对照组。根据以往研究,使用差异模型方法,数学能力测验的第 25个百分位是适合用来甄别学习困难儿童的标准(Geary et al.,2012;Locuniak &Jordan,2008;Swanson &Beebe-Frankenberger,2004),本研究筛查的是数感不良儿童,而非程度更重的数学困难儿童,加之从城乡结合部新移民学校筛选,所以取30%为分界点。

(2)干预阶段

根据儿童数感能力发展的顺序,遵循从具体到抽象的原则,先后进行数量转换和数量估计的干预。本着强调情境性、互动性和趣味性的原则选择数感干预材料并设计游戏性较强的干预步骤,强调儿童在实际情境中依据对数的直觉进行操作和解决直观问题。干预游戏采用回合制方式进行,即一小组4～5名儿童轮流进行操作,方便主试记录、了解每名儿童的情况,在自由游戏环节结束后逐一询问计算过程以了解被试的策略使用和掌握情况,随后给予针对性的反馈。干预在安静的教室里进行,每次干预一个任务,被试掌握某一任务策略后,进入下一任务。每次干预时间约为30～40 min。每周干预2次,持续6周。对数感不良控制组与正常对照组儿童进行故事书阅读,阅读次数和时间与干预组相同。

(3)后测阶段

干预结束一周后随机抽取一套数感测验的复本对3组儿童进行后测,同时施测数集测验。

3.4 结果

3.4.1 不同数感水平儿童前、后测数感成绩的比较

干预前对3组被试的数感水平进行检验,以保证数感不良干预组和控制组儿童的数感水平基本相同。结果显示3组之间差异显著,具体为干预组与控制组在数感各维度和总分上差异均不显著(

p

s＞0.05),且两组与正常组差异均十分显著(

p

s＜0.01)(见表5)。

表5 三组不同数感水平被试在“儿童数感发展测验”上的前、后测成绩比较(M±SD)

考虑到言语、数字记忆和数感前测成绩可能会对被试数感后测成绩有影响,因此,将它们作为协变量对数感后测成绩进行协方差分析以考查干预效果。结果显示,干预组在除了数知识以外的数感其他维度和总分上均显著高于控制组(

p

s＜0.01),且在各维度和总分上与正常组没有差异(

p

s＞0.05)(见表5)。说明干预组经数量转换和数量估计的干预后,数感成绩有了明显提高。为进一步考查3组在前、后测中数感成绩的变化,分别对各组数感前、后测进行相关样本

t

检验,结果显示干预组在数感各维度和总分上的后测成绩与前测相比均有显著提高。相比之下,控制组数感不良儿童虽在数知识、数量转换和数量估计 3个维度中有一定进步(

p

s＜0.05),但却明显低于干预组的促进效果;并且在数数和数型这两个比较难的维度上,没有表现出显著进步。为了考查数感不良干预组与控制组在数感前、后测间的水平增长是否有差异,对两组被试在数感测验各维度和总分上的前、后测增量分数(即表5中的后测分减去前测分)进行

t

检验。结果发现,两组除在数知识维度上没有差异外,其他4个维度和总分上,干预组的增量分都显著高于控制组(

t

=3.52,

p

＜0.001;

t

=4.46,

p

＜0.001;

t

=1.99,

p

＜0.05;

t

=2.84,

p

＜0.01;

t

=7.00,

p

＜0.01),表明干预组明显优于控制组的干预效果。

3.4.2 不同数感水平儿童前、后测计算流畅性的比较

根据 MacMillan (2002),以

d

′作为衡量儿童计算流畅性的指标,

d

′=

Z

–

Z

,表示对目标数量的敏感度,

d

′值越高,计算流畅性就越好。结果发现(见表6),3组被试在计算流畅性前测上差异显著(

F

(2,93)=7.43,

p

＜0.001,η=0.16),数感不良干预组和控制组差异不显著,但二者均与正常组差异显著(

p

＜0.05)。对3组被试计算流畅性后测进行检验发现,组间主效应显著(

F

(2,93)=8.62,

p

＜0.01,η=0.14),事后检验表明,干预组在计算流畅性后测上显著好于控制组(

p

＜0.05),且与正常组差异不显著(

p

＞0.05)。这与如前所述的前测中正常组好于两个数感不良组的结果是不同的,而且这种变化主要体现在数感干预组上的明显进步,表明通过数感任务的干预,干预组被试的计算流畅性水平显著提升,基本达到了正常组的水平。

表6 三组不同数感水平被试在“计算流畅性测验”前、后测的比较(M±SD)

3.4.3 数感和计算流畅性的交叉−滞后相关分析

从上述分析可以看出,3组被试的数感和计算流畅性在后测时都有显著增长,为进一步考查二者之间的关系,明确数感和计算流畅性的相互作用方向,对数感和计算流畅性的发展做交叉−滞后分析(见图1)。

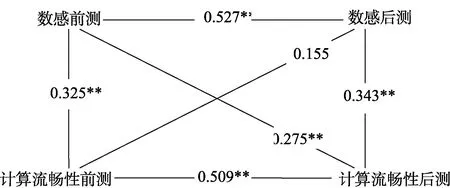
图1 数感和计算流畅性的交叉−滞后相关分析

数感和计算流畅性的前、后测之间的稳定性分别为 β=0.527,

p

＜0.001;β=0.509,

p

＜0.01;β＞β,说明稳定相关一致;数感和计算流畅性的前测、后测的同步性分别为β=0.325,

p

＜0.01;β=0.343,

p

＜0.01,说明同步相关也一致。同步相关和稳定相关一致,符合交叉−滞后组设计的基本假设(Kantowitz,Roediger,&Elmes,1997/2001)。将数感和计算流畅性的前、后测成绩配对,以数感和计算流畅性的前测为自变量,分层先后进入回归方程,先以计算流畅性后测为因变量进行回归分析,结果发现数感前测成绩能够非常显著地预测计算流畅性后测(β=0.275,

p

＜0.01);然后再以数感后测为因变量进行回归分析,发现计算流畅性前测不能预测数感后测(β=0.155,

p

＞0.05)。该结果在一定程度上预示数感可能是计算流畅性的基础。

4 讨论

4.1 信、效度良好的儿童数感发展测验

数学困难是发生在学龄期儿童中的一种学习困难类型,持续时间长、表现明显(American Psychiatric Association,2013)。一个有数学困难的儿童不得不面对与之相关的长期问题,对个体数学成绩改善和升学都有很大的影响。如引言所述,数感是数学困难的强预测变量(Chard et al.,2005;Jordan et al.,2010;Locuniak &Jordan,2008;Seethaler &Fuchs,2010),那么,对儿童数感水平的考核、诊断、甄别和干预就显得格外重要。国外已有的数感测验(如Griffin et al.,1994;Jordan et al.,2008;Malofeeva et al.,2004)试图从幼儿园和小学低年级阶段开始来考查儿童的数感发展状况,以期尽早准确筛查出数感表现不良的、潜在的数学困难风险儿童,并及时进行干预。与西方一些国家不同,中国儿童从幼儿期开始,家庭和幼儿园就十分强调对幼儿数数技能和计算能力的培养,所以国外的数感测验可能并不适合中国儿童。本研究试图考查小学一年级儿童的数感发展水平并对数感发展不良儿童进行干预,这就有必要构建适合中国儿童的数感测验以便识别和筛查数感发展不良儿童。数感测验的内容比同一时期的数学测验所涉及的数字范围要广,在题型设计上要求有新异性,使被测者无法依靠已经学到的算术知识或数字事实直接解决问题。这是采用数感测验考查低龄儿童数学能力并筛查有潜在数学风险儿童的优势。本研究编制的“儿童数感发展测验(一年级用)”主要基于 Jordan等人(Jordan et al.,2006)的五成分理论模型,涵盖了数数、数知识、数量转换、数量估计、数型5个成分,考查的内容有心理数线、有精确计算和数量估计,还有针对算术事实的快速提取等,这比任何单一成分的数学能力测验都具有更好的代表性和更广泛的解释性。

本研究所编制的数感测验采用了双向细目表法,还通过借鉴以往数感测验、参考数学课程标准、专家教师评定等措施来保证内容效度,其效标关联效度验证了数感测验与数感成绩的相关关系,得到了符合测量学标准的两类效度指标。各类信度指标也显示,测验的内部一致性信度、重测信度、复本信度均一致稳定,符合测量学标准。因此,所编制的儿童数感发展测验可以用来评定小学一年级儿童的数感发展水平,并可对数感发展不良儿童进行甄别筛查。

4.2 数量转换和数量估计的动态训练干预对儿童数感发展的促进

为考查经数量转换和数量估计的干预后,数感不良儿童的数感水平和计算流畅性是否提高,本研究将筛查出的数感不良儿童分为干预组和控制组,并与正常对照组进行比较。结果证实了所选干预内容和干预方式的有效性,历经 6周的干预,数感不良干预组在数感5个成分的得分及总分上均有显著提高。而没有接受干预的控制组虽有提高,但在有一定难度的任务(数数和数型)上增长却不显著。我们认为这一增长可能与学校的常规数学教学有关,当然,也不排除自然成熟的影响。数型是数感五成分中的最高成分,考查的是儿童识别数量间关系、根据数量间关系进行推理运算的能力。对低年级儿童来说,这些是比较难的项目,从他们已有的课堂数学知识中实现迁移尚有难度。这时指向于数量转换和数量估计的数感干预便发挥了独特的作用,显示出更明显的效果。根据数感成分依次获得的理论(Jordan et al.,2006,2010),数数维度原本是数感五成分中最基础的维度,但我们在编制项目阶段的预测验中发现,基础性的数数项目对于一年级儿童难度过低,几乎全部答对。因为我国一年级儿童大多于学前期在幼儿园大班或学前班就已接受数学课堂教学,基础性的数数项目对他们还是过于简单,因此便提高了难度。项目涉及到了数数的高级能力,包括依靠所掌握的基数、序数原则来解决数数问题,如,“从3往后数的第5个数是多少？”这无疑提高了对儿童数感能力的要求,他们从常规数学教学中也难以获得直接知识支撑。而此时基于数感干预的训练便显示出了传统数学教学不可替代的优势。再来看数感正常组儿童的成绩,首先他们的数感前测成绩就明显高于数感不良组,尽管没有接受干预训练,但基于自身较高的数感水平,他们在数学教学中的理解、获益和提升会远优于另外两组;另外,“数感”作为一种对数量和数量间关联的意识以及灵活地解决数量问题的能力(Anghileri,2000/2007;Malofeeva et al.,2004),在儿童身上一直不断发展着。所以,除数知识维度外,数感正常组儿童在其他4个数感维度和总分上均有显著增长。至于数知识维度,在前测时该组儿童的成绩就比较高,可发展的空间有限,所以没有表现出显著增长。

本研究选择数量转换和数量估计这两个数感的关键成分作为干预内容,依据的是Jordan等人的主张(如 Locuniak &Jordan,2008;Jordan et al.,2006,2010),数量转换和数量估计对儿童数感水平的预测性最大。同时,在对数学困难的干预方面,Pellegrino和Goldman (1987)也曾提出,对数学困难儿童的补救教学应该包括对算术事实的干预训练。有研究证实,在小学阶段有数学困难倾向的儿童不能自动提取一些算术事实,他们(7岁儿童)所提取的算术事实数量显著低于同龄数学学习正常儿童;且这种差距随年龄的增长而更加明显,到了12岁,数学学习正常的儿童正确提取算术事实的数量是数学困难儿童的3倍(Hasselbring et al.,1988)。研究证实,对算术事实的自动提取对长期的数学成功非常重要(National Mathematics Advisory Panel,2008)。对算术事实不能快速提取严重阻碍了儿童计算流畅性的发展,许多数学困难儿童掌握了程序性知识,但是他们需要以某种方式存储这种信息,才能保证其快速准确地提取。因此,数量转换的动态干预正是帮助这些数感不良儿童将算术事实变为陈述性知识,进而提高计算流畅性水平。

4.3 数感是计算流畅性的基础,是评估年幼儿童数学能力的有效测验内容

研究发现,数感不良能够导致计数加工不足、算术事实提取缓慢、精确计算不足等几乎所有数学困难的特征(Geary,Hamson,&Hoard,2000;Jordan et al.,2003a,2003b)。如前所述,研究已证实数学困难儿童在解决一位数加法问题时的速度和准确性方面都存有缺陷,且与阅读能力无关(Barnes et al.,2006);那些在数学上表现不良的儿童从记忆中检索一位数问题答案的准确度也较低(Carr &Alexeev,2011);同时,计算流畅性不足又是数学学习困难儿童的明显特点(Bryant,2005;Cowan &Powell,2014;Fuchs et al.,2013;Locuniak &Jordan,2008;Reigosa-Crespo et al.,2012)。这些研究都证实了数感和计算流畅性对数学能力、数学困难倾向的预测与影响作用。如前所述,对数学困难的诊断鉴别多年来一直是能力–成绩差异模型占主导,但差异模型因和数学成绩相关对小学低年级儿童并不适用,因此需要更适切敏感的测量指标考查低年级儿童的数学能力。而且,即使在小学低年级,考查和甄别儿童在计算方面是否快速准确也是很容易操作的。那么,计算流畅性是否可以直接用来甄别和诊断年幼儿童的数学困难倾向,筛查潜在数学困难风险儿童？数感测验因涵盖多种数学能力,可以较好地预测年幼儿童的数学能力,是甄别低龄儿童数学困难倾向的良好指标。在这一点上,计算流畅性是否也可以起到类似的作用？为探明此问题,本研究基于动态干预研究对数感和计算流畅性进行了交叉—滞后相关分析,发现了数感对计算流畅性的基础性意义,数感成分中的数量转换和数量估计对计算流畅性有显著的促进作用,支持了前人的研究(如Cowan &Powell,2014;Locuniak &Jordan,2008)。实际上,从另一方面也可以说明计算流畅性不是数感的前提性基础,而是反过来,那些体现数感基本特性的基本数学能力,如列举点数、数值大小比较等对计算流畅性有着较强的影响(Reigosa-Crespo et al.,2012)。厘清这一问题对于诊断和甄别潜在数学困难风险儿童非常重要。数学困难除了有单纯的数学困难和伴阅读困难的两大类别,就单纯的数学困难本身来讲,其表现也存在跨领域的不均衡性(Ginsburg,1997),因为数学的不同方面包括不同的认知能力(Geary et al.,2000),而非只是笼而统之的数学能力(mathematical competence)。比如,有些数学困难儿童表现出算术事实提取的不足,但对数数原则和数学概念把握良好;有些数学困难儿童有良好的计算技能但却不能很好地理解数概念(Jordan &Hanich,2000;Jordan &Montani,1997;Russell &Ginsburg,1984)。所以DSM-Ⅴ提出：诊断数学困难,要列出受损的所有领域和子领域。如果受损领域超过一个,应该根据具体分类——数感、算术事实记忆(memorization of arithmetic facts)、精确或流畅的计算(accurate or fluent calculation)、精确数学推理(accurate math reasoning)——具体指明究竟是哪些领域受损(American Psychiatric Association,2013)。从这里可以看出,数感和计算流畅性虽同为预测低龄儿童数学能力的敏感指标,但属于不同的领域。

这又回到了我们在前言中提到的数感概念的问题——“好识别、难定义”(Case,1998)。不难看出,DSM-Ⅴ中提到的数感与Jordan五成分模型的数感内容是不一样的,后者的成分范围更广,基本涵盖了年幼儿童最基本的数学能力,涉及到数数、数知识、数量转换、数量估计和数型多种数学加工成分。基于五成分模型构建的数感测验,可以相对广泛地说明数学困难的多种表现,且指标明确,所以,以此甄别潜在数学困难风险儿童是可靠和可行的。而计算流畅性是年幼儿童数学能力的外在表现之一,从诊断和筛查角度来讲,计算流畅性,如心理数线(Booth &Siegler,2008)一样,只是良好的预测指标之一,还不能广泛地代表数学认知的能力范畴,而更为基础和范畴广泛的数感评估则更为适合。我们通过研究证实了数感是计算流畅性的基础,为数感在评估测量中的可靠意义提供了前提性依据。依据五成分理论模型编制的数感测验,包含数感的多种成分,有心理数线、有精确计算和数量估计、有数数技能等,以此评估潜在数学困难风险儿童,比任何单一成分的数学能力测验都具有更好的代表性和更广泛的解释性。而且数感测验的各个成分已被证明和数学能力关系密切——如,早期的

数数

困难可以预测日后的算术运算困难(Geary,Hoard,&Hamson,1999);

数知识

是一年级算术成绩的强预测变量(零阶相关系数达0.73) (Baker et al.,2002);与语言相关的

数量转换

涉及到了经验和学习对数学能力的意义,与非言语计算有关的

数量转换

则考查了与工作记忆有关的数量表征能力;

数估计

与要求精确数知识的算术运算技能有显著相关(Dowker,1997);

数型

的掌握可以使数字组合变得更加流畅(Gray &Tall,1994;Jordan et al.,1994)——也强有力地支持了数感测验作为评估和筛查工具的有效价值。

最后,需要特别强调的是,在深入小学数学教学实践的过程中,我们发现数学教师对数感促进数学能力的显著意义还没有充分的认识,对儿童数感的培养和训练还处在无意识教学阶段。事实上,培养和训练儿童的数感不但有利于他们将已有数学知识进行良好的迁移,而且有利于他们在科技高度发达的社会中为今后的生活和工作打好基础、做好准备(Anghileri,2000/2007)。因此,全美数学教师协会(NCTM) National Council of Teachers of Mathematics (NCTM).(1994)..Reston,VA:Author.1994年就提出了从学龄前到高中阶段的数感教学建议,我国也于 2001年将数感教学写入了全日制义务教育数学课程标准 中华人民共和国教育部.(2001)..北京:北京师范大学出版社.,将数感的形成作为学校数学课程改革的主要目标之一。因此,在数学教学中大力强调估算和数感的训练势在必行,本研究在数感干预内容和干预手段上的研究正是服务于数感教学的有益探索。

5 结论

(1)所编制的涉及数感多种成分的“儿童数感发展测验(一年级用)”信、效度良好,可以有效评估儿童的数感发展状况,并区分出不同数感发展水平的儿童;

(2)通过对数感不良儿童进行指向于数量转换和数量估计的动态干预,其数感水平得到显著提高,并且计算流畅性水平也得到提高;

(3)数感是计算流畅性的基础和预测变量。

American Psychiatric Association.(2013).

Diagnostic and statistical manual of mental disorders

(5th ed.).Arlington:American Psychiatric Publishing.Anghileri,J.(Ed.).(2007).

Teaching number sense

(W.B.Xu,Trans.).Beijing,China:Beijing Normal University Press.(Original work published 2000).[安吉莱瑞,J.(主编).(2007).

如何培养学生的数感

(徐文彬译).北京:北京师范大学出版社.]Baker,S.,Gersten,R.,Flojo,J.,Katz,R.,Chard,D.,&Clarke,B.(2002).

Preventing mathematics difficulties in young children:Focus on effective screening of early number sense delays

.(Technical Report No.0305).Eugene,OR:Pacific Institutes for Research.Barnes,M.A.,Wilkinson,M.,Khemani,E.,Boudesquie,A.,Dennis,M.,&Fletcher,J.M.(2006).Arithmetic processing in children with spina bifida:Calculation accuracy,strategy use,and fact retrieval fluency.

Journal of Learning Disabilities,39

(2),174–187.Berch,D.B.(2005).Making sense of number sense:Implications for children with mathematical disabilities.

Journal of Learning Disabilities,38

(4),333–339.Bi,Y.,&Zhang,L.J.(2014).Problems and strategies on identifying mathematics learning disabilities with the ability-achievement discrepancy models.

Chinese Journal of Special Education,

(5),49–54.[毕远,张丽锦.(2014).以能力-成绩差异模型鉴别数学困难的问题与对策.

中国特殊教育,

(5),49–54.]Booth,J.L.,&Siegler,R.S.(2008).Numerical magnitude representations influence arithmetic learning.

Child Development,79

(4),1016–1031.Bryant,D.P.(2005).Commentary on early identification and intervention for students with mathematics difficulties.

Journal of Learning Disabilities,38

(4),340–345.Carr,M.,&Alexeev,N.(2011).Fluency,accuracy,and gender predict developmental trajectories of arithmetic strategies.

Journal of Educational Psychology,103

(3),617–631.Case,R.(1998).

A psychological model of number sense.

Paper presented at the annual meeting of the American Educational Research Association,San Diego,CA.Case,R.,&Griffin,S.(1990).Child cognitive development:The role of central conceptual structures in the development of scientific and social thought.

Advances in Psychology,64

,193–230.Chan,W.W.L.(2014).Understanding and processing numbers among chinese children.

Psychology &Neuroscience,7

(4),583–591.Chard,D.J.,Clarke,B.,Baker,S.,Otterstedt,J.,Braun,D.,&Katz,R.(2005).Using measures of number sense to screen for difficulties in mathematics:Preliminary findings.

Assessment for Effective Intervention,30

(2),3–14.Chen,G.P.,&Li,D.(1994).The revision of the Chinese norm of McCarthy scale of children’s abilities.

Chinese Journal of Clinical Psychology,2

(3),135–140.[陈国鹏,李丹.(1994).麦卡锡儿童智能量表的修订.

中国临床心理学杂志,2

(3),135–140.]Codding,R.S.,Chan-Iannetta,L.,George,S.,Ferreira,K.,&Volpe,R.(2011).Early number skills:Examining the effects of class-wide interventions on kindergarten performance.

School Psychology Quarterly,26

(1),85–96.Cowan,R.,&Powell,D.(2014).The contributions of domaingeneral and numerical factors to third-grade arithmetic skills and mathematical learning disability.

Journal of Educational Psychology,106

(1),214–229.Dowker,A.(1997).Young children's addition estimates.

Mathematical Cognition,3

(2),140–153.Dyson,N.I.,Jordan,N.C.,&Glutting,J.(2013).A number sense intervention for low-income kindergartners at risk for mathematics difficulties.

Journal of Learning Disabilities,46

(2),166–181.Fuchs,L.S.,Geary,D.C.,Compton,D.L.,Fuchs,D.,Schatschneider,C.,Hamlett,C.L.,...Changas,P.(2013).Effects of first-grade number knowledge tutoring with contrasting forms of practice.

Journal of Educational Psychology,105

(1),58–77.Geary,D.C.(1995).Reflections of evolution and culture in children's cognition:Implications for mathematical development and instruction.

American Psychologist,50

(1),24–37.Geary,D.C.(2006).Development of mathematical understanding.In D.Kuhl &R.S.Siegler (Vol.Eds.) &W.Damon (Gen.Ed.),

Cognition,perception,and language,Vol 2:Handbook of child psychology

(6th ed.,pp.777–810).New York:John Wiley &Sons.Geary,D.C.(2011).Cognitive predictors of achievement growth in mathematics:A 5-year longitudinal study.

Developmental Psychology,47

,1539–1552.Geary,D.C.,Bailey,D.H.,&Hoard,M.K.(2009).Predicting mathematical achievement and mathematical learning disability with a simple screening tool:The Number Sets Test.

Journal of Psychoeducational Assessment,27

(3),265–279.Geary,D.C.,Bow-Thomas,C.C.,Liu,F.,&Siegler,R.S.(1996).Development of arithmetical competencies in Chinese and American children:Influence of age,language,and schooling.

Child Development,67

(5),2022–2044.Geary,D.C.,Boykin,A.W.,Embretson,S.,Reyna,V.,Siegler,R.,Berch,D.B.,&Graban,J.(2008).

Report of the task group on learning processes.

Download from http://www2.ed.gov/about/bdscomm/list/mathpanel/report/l earning-processes.pdfGeary,D.C.,Hamson,C.O.,&Hoard,M.K.(2000).Numerical and arithmetical cognition:A longitudinal study of process and concept deficits in children with learning disability.

Journal of Experimental Child Psychology,77

(3),236–263.Geary,D.C.,&Hoard,M.K.(2005).Learning disabilities in arithmetic and mathematics:Theoretical and empirical perspectives.In J.I.D.Campbell (Ed.),

Handbook of mathematical cognition

(pp.253–267).New York:Psychology Press.Geary,D.C.,Hoard,M.K.,&Hamson,C.O.(1999).Numerical and arithmetical cognition:Patterns of functions and deficits in children at risk for a mathematical disability.

Journal of Experimental Child Psychology,74

(3),213–239.Geary,D.C.,Hoard,M.K.,Nugent,L.,&Bailey,D.H.(2012).Mathematical cognition deficits in children with learning disabilities and persistent low achievement:A five-year prospective study.

Journal of Educational Psychology,104

(1),206–223.Gelman,R.,&Butterworth,B.(2005).Number and language:How are they related?

Trends in Cognitive Sciences,9

(1),6–10.Gersten,R.,Jordan,N.C.,&Flojo,J.R.(2005).Early identification and interventions for students with mathematics difficulties.

Journal of Learning Disabilites,38

(4),293–304.Ginsburg,H.P.(1997).Mathematics learning disabilities:A view from developmental psychology.

Journal of Learning Disabilities,30

(1),20–33.Gray,E.M.,&Tall,D.O.(1994).Duality,ambiguity,and flexibility:A "proceptual" view of simple arithmetic.

Journal for Research in Mathematics Education,25

,116–140.Griffin,S.A.,Case,R.,&Siegler,R.S.(1994).Rightstart:Providing the central conceptual prerequisites for first formal learning of arithmetic to students at risk for school failure.In K.McGilly (Ed.),

Classroom lessons:Integrating cognitive theory and classroom practice

(pp.24–49).Cambridge,MA:MIT Press.Hanich,L.B.,Jordan,N.C.,Kaplan,D.,&Dick,J.(2001).Performance across different areas of mathematical cognition in children with learning difficulties.

Journal of Educational Psychology,93

(3),615–626.Hasselbring,T.S.,Goin,L.,&Bransford,J.D.(1988).Developing math automaticity in learning handicapped children:The role of computerized drill and practice.

Focus on Exceptional Children,20

(6),1–7.Jordan,N.C.,Glutting,J.,Dyson,N.,Hassinger-Das,B.,&Irwin,C.(2012).Building kindergartners' number sense:A randomized controlled study.

Journal of Educational Psychology,104

(3),647–660.Jordan,N.C.,Glutting,J.,&Ramineni,C.(2008).A number sense assessment tool for identifying children at risk for mathematical difficulties.In A.Dowker (Ed.),

Mathematical difficulties:Psychology and intervention

(pp.45–58).San Diego,CA:Academic Press.Jordan,N.C.,Glutting,J.,&Ramineni,C.(2010).The importance of number sense to mathematics achievement in first and third grades.

Learning and Individual Differences,20

(2),82–88.Jordan,N.C.,&Hanich,L.B.(2000).Mathematical thinking in second-grade children with different forms of LD.

Journal of Learning Disabilities,33

(6),567–578.Jordan,N.C.,&Hanich,L.B.(2003).Characteristics of children with moderate mathematics deficiencies:A longitudinal perspective.

Learning Disabilities Research &Practice,18

(4),213–221.Jordan,N.C.,Hanich,L.B.,&Kaplan,D.(2003a).A longitudinal study of mathematical competencies in children with specific mathematics difficulties versus children with comorbid mathematics and reading difficulties.

Child Development,74

(3),834–850.Jordan,N.C.,Hanich,L.B.,&Kaplan,D.(2003b).Arithmetic fact mastery in young children:A longitudinal investigation.

Journal of Experimental Child Psychology,85

(2),103–119.Jordan,N.C.,Kaplan,D.,Oláh,L.,&Locuniak,M.N.(2006).Number sense growth in kindergarten:A longitudinal investigation of children at risk for mathematics difficulties.

Child Development,77

(1),153–175.Jordan,N.C.,Levine,S.C.,&Huttenlocher,J.(1994).Development of calculation abilities in middle-and low-income children after formal instruction in school.

Journal of Applied Developmental Psychology,15

(2),223–240.Jordan,N.C.,&Montani,T.O.(1997).Cognitive arithmetic and problem solving:A comparison of children with specific and general mathematics difficulties.

Journal of Learning Disabilities,30

(6),624–634.Kantowitz,B.H.,Roediger,B.H.,&Elmes,D.G.,(Eds).(2001).

Experimental psychology

:

Access to psychological research

(X.Y.Guo,et al.Trans).(p.55).Shanghai,China:East China Normal University Press.(Original work published 1997)[坎特威茨,B.H.,罗迪格,B.H.,埃尔姆斯,D.G.(主编).(2001).

实验心理学——掌握心理学的研究

(郭秀艳 等译).(p.55).上海:华东师范大学出版社.]Kilpatrick,J.,Swafford,J.,&Findell,B.(Eds.).(2001).

Adding it up:Helping children learn mathematics

(pp.140–153).Washington,DC:National Academies Press.Landerl,K.,Bevan,A.,&Butterworth,B.(2004).Developmental dyscalculia and basic numerical capacities:A study of 8–9-year-old students.

Cognition,93

(2),99–125.Levine,S.C.,Jordan,N.C.,&Huttenlocher,J.(1992).Development of calculation abilities in young children.

Journal of Experimental Child Psychology,53

(1),72–103.Locuniak,M.N.,&Jordan,N.C.(2008).Using kindergarten number sense to predict calculation fluency in second grade.

Journal of Learning Disabilities,41

(5),451–459.Macmillan,N.A.(2002).Signal detection theory.In J.Wixted(Ed.),

Stevens’ handbook of experimental psychology (Vol.4):Methodology in experimental psychology

(3rd ed.,pp.43–90).New York:John Wiley &Sons,Inc.Malofeeva,E.,Day,J.,Saco,X.,Young,L.,&Ciancio,D.(2004).Construction and evaluation of a number sense test with head start children.

Journal of Educational Psychology,96

(4),648–659.Mazzocco,M.M.M.,&Thompson,R.E.(2005).Kindergarten predictors of math learning disability.

Learning Disabilities Research and Practice,20

(3),142–155.McNeil,N.M.,Fyfe,E.R.,&Dunwiddie,A.E.(2015).Arithmetic practice can be modified to promote understanding of mathematical equivalence.

Journal of Educational Psychology,107

(2),423–436.National Mathematics Advisory Panel.(2008).

Foundations for success:Final report of the National Mathematics Advisory Panel.

Washington,DC:United States Department of Education.Pellegrino,J.W.,&Goldman,S.R.(1987).Information processing and elementary mathematics.

Journal of Learning Disabilities,20

(1),23–32.Ramani,G.B.,Siegler,R.S.,&Hitti,A.(2012).Taking it to the classroom:Number board games as a small group learning activity.

Journal of Educational Psychology,104

(3),661–672.Reigosa-Crespo,V.,Valdés-Sosa,M.,Butterworth,B.,Estévez,N.,Rodríguez,M.,Santos,E.,...Lage,A.(2012).Basic numerical capacities and prevalence of developmental dyscalculia:The havana survey.

Developmental Psychology,48

(1),123–135.Rodic,M.,Zhou,X.L.,Tikhomirova,T.,Wei,W.,Malykh,S.,Ismatulina,V.,...Kovas,Y.(2015).Cross-cultural investigation into cognitive underpinnings of individual differences in early arithmetic.

Developmental Science,18

,165–174.Russell,R.L.,&Ginsburg,H.P.(1984).Cognitive analysis of children's mathematics difficulties.

Cognition and Instruction,1

(2),217–244.Seethaler,P.M.,&Fuchs,L.S.(2010).The predictive utility of kindergarten screening for math difficulty.

Exceptional Children,77

(1),37–59.

Sowder,J.(1992).Making sense of numbers in school

mathematics.In G.Leinhardt,R.Putman,&R.A.Hattrup(Eds.),

Analysis of arithmetic for mathematics teaching

(pp.1–51).Hillsdale,New Jersey:Lawrence Erlbaum Associates.Swanson,H.L.,&Beebe-Frankenberger,M.(2004).The relationship between working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties.

Journal of Educational Psychology,96

(3),471–491.Zhao,Z.G.(2008).The study on the development of number sense in young children aged 3-6.

Psychological Development and Education,24

(4),8–12.[赵振国.(2008).3～6岁儿童数感发展的研究.

心理发展与教育,24

(4),8–12.]Zhou,G.D.,Mo,L.,&Wen,H.B.(2009).Representational patterns of numerical estimation and its development in children.

Psychological Development and Education,25

(4),21–29.[周广东,莫雷,温红博.(2009).儿童数字估计的表征模式与发展.

心理发展与教育,25

(4),21–29.]Zhou,X.,Huang,J.,Zhao,Z.G.,&Yang Z.H.(2009).On development of 6-year-old children’s mathematical cognition.

Early Childhood Education (Educational Sciences),(11)

,35–39.[周欣,黄瑾,赵振国,杨宗华.(2009).大班儿童数学认知的发展.

幼儿教育(教育科学),(11)

,35–39.]