基于ADAMS的Ø335钢管端面倒棱机自动输送机构的优化设计

基于ADAMS的φ335钢管端面倒棱机自动输送机构的优化设计

郑帅1,2，柴晓艳1,2，刘锡军1,2，元磊1,2

(1．天津理工大学 天津市先进机电系统设计与智能控制重点实验室 天津 300384； 2.天津理工大学 机械工程学院，天津 300384)

摘要：自动输送机构是钢管倒棱机中重要组成部分，运用ADAMS软件建立了自动输送机构的虚拟样机模型，进行仿真分析、优化设计，优化后降低了输送机构原动件的驱动力，使升降过程最大升降力降低了62.9%，平均升降力降低了59.4%，使推进过程最大推进力降低了74.8%,平均推进力降低了72.7%。

关键词：输送机构；钢管倒棱机；优化设计；仿真分析

中图分类号：TG502文献标识码：A

收稿日期：2015-04-27；修订日期：2015-06-19

基金项目：2014年天津市中小型创新

作者简介：郑帅(1990-)，男，天津理工大学硕士研究生。

ADAMS-based optimal design for automatic conveying mechanism ofφ335 steel pipe end chamfering machine

ZHENG Shuai1,2, CHAI Xiao-yan1,2, LIU Xi-jun1,2, YUAN Lei1,2

(1.Tianjin Key Laboratory of the Design and Intelligent Control of the Advanced Mechatronical System,

Tianjin University of Technology, Tianjin 300384, China;

2. School of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384,China)

Abstract：Automatic conveying mechanism is an important part of steel pipe end chamfering machine. ADAMS software is applied to establish the model of virtual prototype of automatic conveying mechanism. Then the simulation analysis and optimal design have been completed. The driving force of conveying mechanism is reduced through the optimization. The maximum lifting force of lifting process is reduced by 62.9%, and the average lifting force is decreased by 59.4%. The maximum propulsive force of progradation is reduced by 74.8%, and the average propulsive force is decreased by 72.7%.

Keywords：conveying mechanism; pipe chamfering machine; optimal design; simulation analysis

0前言

随着国民经济的快速发展，钢管的产量与日俱增，2014年我国钢管产量达到了8898.01万吨，钢管端面倒棱机是对钢管两端进行平头、倒棱、去毛刺的机构，可提高钢管的附加值，扩展钢管更广泛的用途，钢管自动输送机构是钢管端面倒棱机的重要组成部分[1]。本文对钢管自动输送机构在ADAMS中进行了参数化建模，对输送机构液压缸的驱动力采取两种优化方案，通过比较两种优化方案的结果，可以为改进输送机构提供最优的方案[2]，实现最大程度降低液压缸能耗的目的，得到优化的钢管自动输送机构。

1自动输送机构的工作过程

自动输送机构如图1所示，钢管端面倒棱机由自动输送机构、铣头加工机构和夹紧机构三部分组成。由于摆杆1、3长度相等且平行布置，故杆1、2、3和机架AD组成平行四边形机构，当活塞杆5伸缩时，带动摆杆1、3摆动，1、3杆摆动时带动连杆2水平升降，杆1、2、3、5、9和机架组成了升降机构。连杆2分为前后对称的两个杆件，在这两个杆件之间有滚子(图中未画出)分布于B、C两端，滑移块4被滚子支撑，滑移块4上有V型块，滑移块4随杆2水平升降，当活塞杆8伸缩时，带动摆杆7摆动，摆杆7通过连杆6带动滑移块4水平移动，由于滑移块4是支撑在滚子上，所以滑移块4水平移动时，将产生滚动摩擦。杆6、7、8、10、滑移块4和机架组成推进机构。

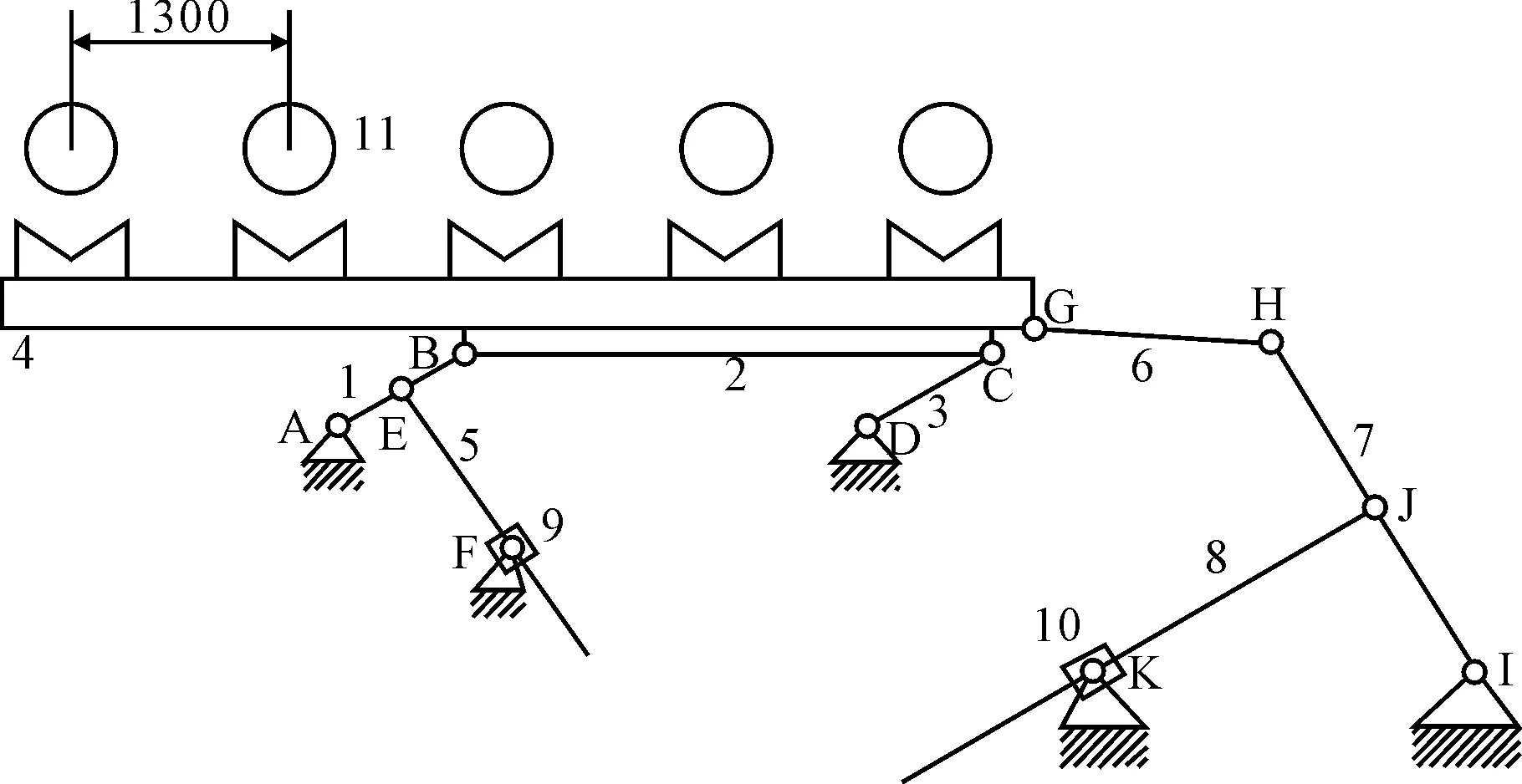
1.摆杆 2.连杆 3.摆杆 4.滑移块 5.活塞杆 6.连杆 7.摆杆 8.活塞杆 9.液压缸 10.液压缸 11.钢管 图1　φ335自动输送机构简图 Fig.1　Diagram of φ335 automatic conveying mechanism

机构的运动过程包括4个行程，第一行程：活塞杆5驱动杆1，带动升降机构上升，上升至接触钢管后，继续上升至杆1、3到达垂直位置，然后活塞杆5停止驱动，则第一行程结束。第二行程：液压缸10驱动杆7，带动推进机构向右水平移动，移动1 300 mm后，液压缸10停止驱动，则第二行程结束[3]。第三行程：活塞杆5开始收缩，带动滑移块4和钢管11开始水平下降，下降到钢管接触夹紧装置的V型槽时(图中未画V型槽)，钢管被V型槽拖住，然后铣头加工机构开始对钢管两端进行平头、倒棱等工作，同时滑移块4上的V型块与钢管11脱离，继续下降到杆1、3回到初始位置，完成第三行程运动。最后推进机构反向(向左)水平移动一个步进距离，完成最后一个行程运动，等待下一周期的输送运动。

2升降机构的优化设计

2.1优化目标

建立升降机构模型，如图2所示。由于要使得当杆1、3到达垂直位置时机构停止运动，为此要建立对杆1角度的测量，使用ADAMS的传感器监测该角度，使得当杆1与水平方向夹角为90°时，机构停止运动。进行运动学仿真，并建立对活塞杆5的推进力测量，得到活塞杆5在升降运动中推进力随时间变化的曲线，如图3所示。图3中出现峰值的时刻为滑移块4上的V型块刚接触钢管的那一刻，钢管产生了一个瞬时加速度，根据牛顿第二定律，活塞杆5所出推进力瞬时达到最大值，该最大值为48 677.851 8 N[4]。活塞杆5在运动过程中保持匀速运动，通过图3可以看出其推进力在升降过程中是变化的。升降机构的优化目标是液压缸9的最大推进力，优化目的是该最大推进力为最小，通过优化原动件液压缸的安装位置以及升降机构相关铰链点的位置，实现活塞杆5中最大推进力为最小，从而实现降低液压缸能耗的目的。

图2　升降机构模型 Fig.2　Lifting mechanism model

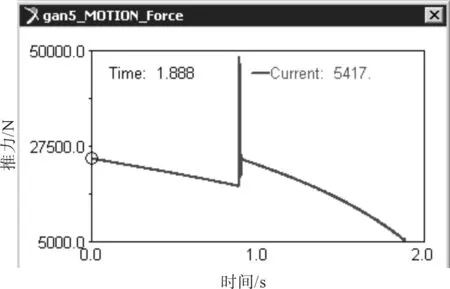
图3　活塞杆5的推进力变化曲线 Fig.3　Curve of propulsion force from piston rod 5

2.2参数化建模

根据优化目标，对升降机构相关铰链点的坐标进行参数化，参数化后得到相应的设计变量，参数化的铰链点如图4所示[5]。

对F点的y坐标进行参数化，F点y坐标的变化可以改变杆5的倾斜角度，故不需要对F点的x坐标进行优化。当铰链点E、F发生变化时，杆5与水平方向的夹角α在变化，由图4可知：

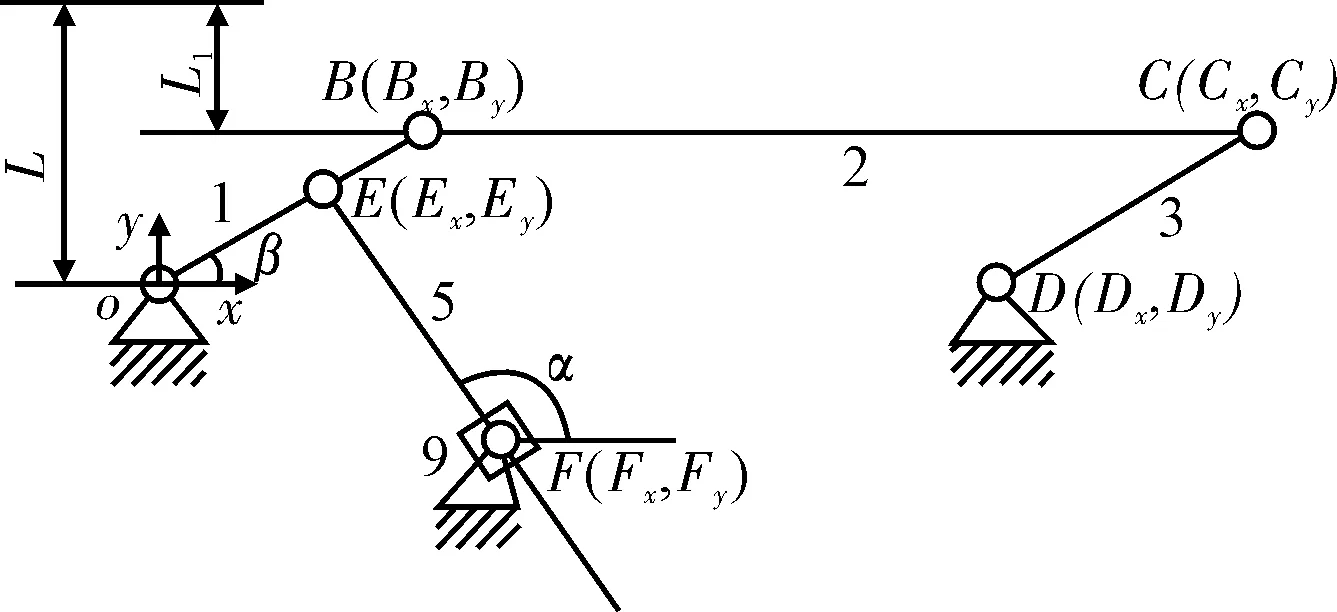
图4　升降机构参数关系几何图形 Fig.4　Geometric figure for parameters relationship of lifting mechanism

E点进行参数化后得到设计变量Ex、Ey，设计变量Ex的变化会带动Ey的变化，其结果是E点始终保持在杆1上[6]。杆1与水平方向的夹角设为β，其相互关系如图4所示。

Ey=tanβ*Ex

D点是为了改变杆长而设置的参数化点，对D点的x坐标进行参数化。

B点进行参数化后得到设计变量Bx、By，设计变量By的变化会带动Bx和β的变化。机构的行程是一定的，即图中的L1值，由夹紧机构来确定该行程，当管径给定时，该行程是确定的。设杆1长度为L,由图4可得：

L-L1=By

By/sinβ-L1=By

由图也可确定Bx值，即

Bx=By/tanβ

C点是为了改变杆长而设置的参数化点，对C点的x、y坐标分别进行参数化，由于杆1和杆3始终保持平行，所以该机构B点和C点对应的设计变量应该保持同步变化，由图4可得

Cx=Dx+Cy/tanβ

Cy=By

由此完成了升降机构的参数化建模。

2.3优化设计

在参数化建模中，建立了设计变量，设计变量包括因变量和自变量，因变量用自变量的表达式来表达，优化前需要对每个自变量进行敏感度分析，通过自变量初始值处的敏感度大小来确定需要优化的自变量。

2.3.1确定优化参数

由以上分析可知，设计变量Fy、Ex、Dx、By是自变量，对4个设计变量进行敏感度分析，测得设计变量在初始值处的敏感度，结果见表1。

表1　设计变量敏感度

由表1可知，敏感度较大的自变量是Fy、Ex、By，这三个自变量对优化结果的影响较大，Dx的敏感度较小，在设计研究报告中，Dx的值增加10%，即机构在x方向杆长增加10%，活塞杆5的最大力变化仅为1.97%，这说明Dx对机构的影响较小，故舍去Dx，优化参数只有Fy、Ex、By[7]。其中By是与机构整体尺寸有关的参数 ，因此采取两种优化方案：第一种，对机构整体尺寸进行优化，即对设计变量Fy、Ex、By进行优化；第二种，不对机构整体尺寸进行优化，只对机构局部尺寸进行优化，即对设计变量Fy、Ex进行优化。

2.3.2确定优化参数取值范围

根据图1和图4分析，Fy应该在纵坐标Ky(该标注点见图9)与By之间变化，故Fy的取值范围为(-856，By)。Ex应该在杆1上变化，但Ex不能过小，否则活塞杆5推不动杆1，故Ex的取值范围为(150，Bx)。By是该机构在y方向上的杆长增量，这个增量值不能太大，否则就会使整个机构包括与之配套的设备整体增大，因此设定在±10%之内变化。

2.3.3优化计算和分析

两种优化方案的操作步骤相同，在完成参数化分析的准备工作以后，便可以进行优化计算。

(1)按照第一种优化方案，对机构整体尺寸进行优化，即对Fy、Ex、By进行优化后，得到升降机构活塞杆5在迭代过程中的最大推进力变化曲线。

从设计研究报告可以看出，优化后各个设计变量的取值以及对应的最大推进力，结果见表2。

表2　升降机构第一种优化结果

从表2可以看出，优化后Fy、Ex和By都发生了变化，By增加了10%。通过优化最大推进力降低了69.9%，平均推进力降低了49.2%。优化后总能耗为

W=Fvt=7273.4276J

式中，F为推进过程中的平均力，F=9 512.473 7 N；v为推进速度，v=0.2 m/s；t为推进时间，t=3.8231s[8]。

(2)按照第二种优化方案，对机构局部尺寸进行优化，即对Fy、Ex进行优化后，得到升降机构活塞杆5在迭代过程中的最大推进力变化曲线。

从设计研究报告可以看出，优化后各个设计变量的取值以及对应的最大推进力，结果见表3。

表3　升降机构第二种优化结果

从表3可以看出，优化后Fy、Ex都发生了变化，通过优化最大推进力降低了62.9%，平均推进力降低了59.4%。优化后总能耗为

W=Fvt=5932.7961J

其中，F=7598.745 N；v=0.2 m/s；t=3.9038 s。

两种优化方案的比较见表4。

从表4可以看出，虽然第一种优化方案的最大力比第二种小，但是第一种优化方案的能耗比第二种高1 340.631 5 J，第二种优化方案更节能，故采用第二种优化方案，即对升降机构采用局部尺寸优化方案。

表4　升降机构的两种优化结果对比

3推进机构的优化设计

3.1优化目标

建立推进机构模型，如图5所示。建立对活塞杆8推进力的测量，进行运动学仿真，得到活塞杆8推进力在推进运动中的变化曲线，如图8所示。曲线在起始阶段出现最大力是因为此时推进机构刚开始拉动钢管，钢管需要产生一个突变加速度，根据牛顿第二定律，故活塞杆8的出力在此时产生突变导致出现最大力，最大力为14 657.025 8 N。活塞杆8在推进过程中保持匀速运动，从图6可以看出，活塞杆8在运动过程中的驱动力是变化的。对于活塞杆8，其出力大小与其安装位置及杆6、7、8的相对位置关系和杆6、7的长度有关。活塞杆8的安装位置由铰链J、K决定，推进机构的优化目标是液压缸10的最大推进力，优化目的是要使得该最大推进力为最小，通过优化原动件液压缸的安装位置以及推进机构相关铰链点的位置，实现活塞杆8中最大推进力为最小，从而实现降低液压缸能耗的目的

图5　推进机构模型 Fig.5　Propulsion mechanism model

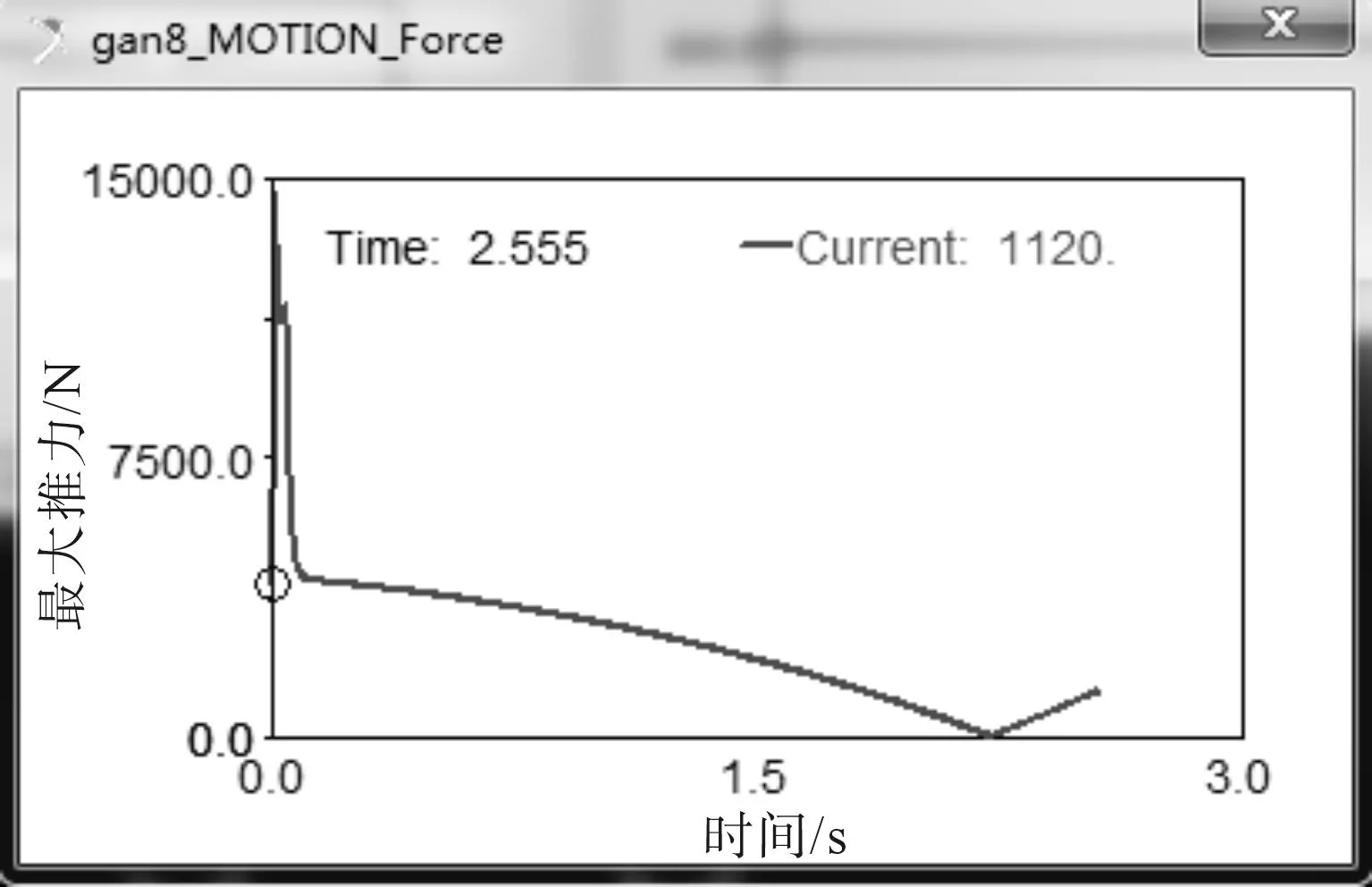
图6　活塞杆8推进力的变化曲线 Fig.6　Curve of propulsion force from piston rod 8

3.2参数化建模

根据优化目标，我们对推进机构相关铰链点的坐标进行参数化，参数化后得到相应的设计变量，参数化的铰链点如图7所示。在图7中，由于要使推进机构前进一个步进距离L2后机构停止运动，为此要建立对滑移块4的位移测量，使用传感器监测该位移到达一个步进距离时，机构停止运动，即用传感器监测滑移块4中的G点前进一个步进距离L2到达G’点时，让机构停止运动[9]。

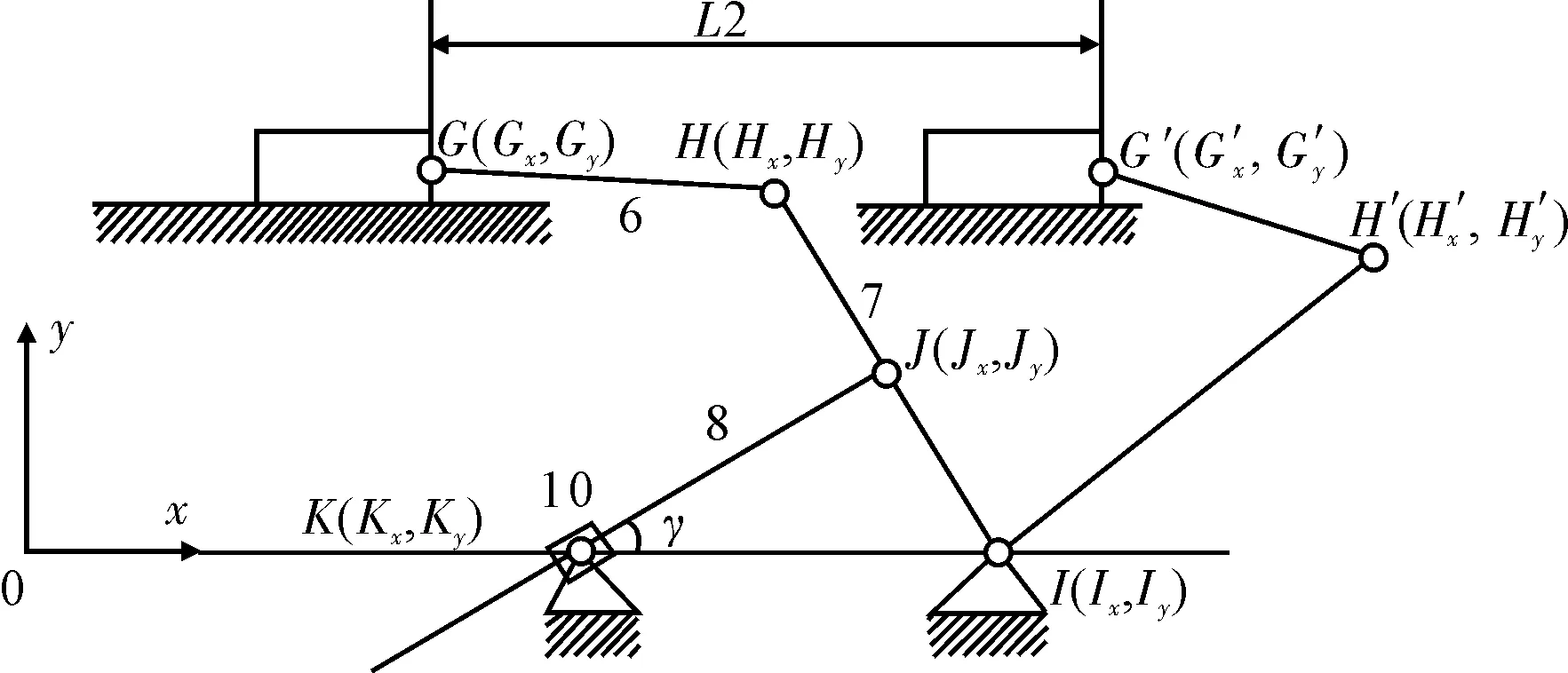
图7　推进机构参数关系几何图形 Fig.7　Geometric figure for parameters relationship of propulsion mechanism

K点的y坐标Ky进行参数化，Ky的变化结果是使活塞杆的倾斜角度改变，故K点的x坐标不需要优化，在x方向上找一个合适的安装点即可。

J点的x、y坐标进行参数化后得到设计变量Jx、Jy，设计变量Jx的变化会带动Jy的变化，变化的结果是J点始终在杆7上。

H点是为了改变杆长而设置的参数化点，对H点的x、y坐标进行参数化，Hx、Hy可以同时改变杆6、7在x方向和y方向的长度，Hx、Hy变化时，H点始终保持在杆7上，由图7可得

即

3.3优化设计

3.3.1确定优化参数

由以上分析可知，我们确定自变量为Ky、Jx、Hx、Hy，对每个自变量进行敏感度分析，测得设计变量在初始值处的敏感度，结果见表5。

表5　设计变量的敏感度

从表5可以看出，设计变量Ky、Jx、Hx和Hy的敏感度都较大，故四个设计变量对活塞杆8的出力影响都较大。其中Hx、Hy是与机构整体尺寸有关的参数 ，因此采取两种优化方案：第一种，对机构整体尺寸进行优化，即对设计变量Ky、Jx、Hx和Hy进行优化；第二种，不对机构整体尺寸进行优化，只对机构局部尺寸进行优化，即对设计变量Ky、Jx进行优化。

3.3.2确定优化参数取值范围

Ky的变化范围是Iy到Hy之间，故Ky的取值范围是(-856，Hy)。Jx在杆7上变化，但Jx不能太接近Ix，太接近会导致活塞杆8推不动7杆，故Jx的取值范围是(Hx，5200)。Hx和Hy是为了改变杆件在x方向和y方向的长度而设置的变量，杆长过小，不能满足推进行程的要求，杆长过大会使整个机构和相关配套设备尺寸增大，故取值范围是原杆长度的±10%[10]。

3.3.3优化分析和计算

两种优化方案的操作步骤相同，在完成参数化分析的准备工作以后，便可以进行优化计算。

(1)按照第一种优化方案，对推进机构整体尺寸进行优化，即对设计变量Ky、Jx、Hx和Hy进行优化，得到迭代过程中推进机构活塞杆8最大力的变化曲线。

从设计研究报告可以看出，优化后各个设计变量的取值以及对应的推进机构的最大推进力，见表6。

表6　推进机构第一种优化结果

从表6可以看出，优化后各个设计变量的值都发生变化，Hx减小2.2%，Hy增加4.9%。通过优化，推进机构活塞杆8的最大力降低了74.8%，平均力降低了72.7%。优化后总能耗为

W=Fvt=708.982 3 J

其中，F=689.926 6 N；v=0.2 m/s；t=5.138 1 s。

(2)按照第二种优化方案，对推进机构局部尺寸进行优化，即对设计变量Ky、Jx进行优化，得到迭代过程中活塞杆8最大力的变化曲线。

从优化设计报告可以看出，优化后各个设计变量的取值以及对应的推进机构最大力，见表7。

表7　推进机构第二种优化结果

从表7可以看出，优化后各个设计变量的取值都发生变化。通过优化，推进机构活塞杆8的最大力降低了70.3%，平均力降低了66.6%。优化后的总能耗为

W=Fvt=842.0978 J

其中，F=843.4473 N；v=0.2 m/s；t=4.992 s[11]。

推进机构两种优化结果比较见表8。

表8　推进机构两种优化结果比较

从表8可以看出，第一种优化方案的最大力比第二种小，而且第一种优化方案的能耗比第二种少133.115 5 J，故采用第一种优化方案，即对推进机构采用整体尺寸优化方案。

4结论

本文利用ADAMS软件建立了φ335钢管端面倒棱机自动输送机构的仿真分析模型，对升降机构和推进机构分别进行了整体尺寸和局部尺寸的优化。根据优化结果，对升降机构采用局部尺寸优化方案，此优化方案节能效果更明显，优化后升降机构的最大载荷由原先的48 677.851 8 N减少到18 081.5 N，减少了62.9%，平均载荷由原先的18 730.907 5 N减少到7 598.745 N，减少了59.4%。对推进机构采用整体尺寸优化方案，优化后推进机构的最大载荷由原先的14 657.025 8N减少到3 695.65 N，减少了74.8%，平均载荷由原先的2 525.589 9 N减少到689.926 6 N，减少了72.7%。将优化的结果数据应用到选择机构的标准件上，同时还可以将结果数据应用到零件的强度校核上。目前已将该优化结果应用到φ335钢管端面倒棱机上。

参考文献：

[1]余小巧. 全自动钢管端面铣头机自动送料机构的优化设计[D].天津：天津理工大学，2011：2-4.

[2]芮成杰，柴晓艳．钢管端面铣头倒棱机夹紧机构的优化设计[J]．重型机械，2012(06)：43-48.

[3]张显峰.φ610全自动钢管端面铣头自动送料机构的优化设计[D].天津：天津理工大学，2012:4-7 .

[4]李军，邢俊文，覃文洁．ADAMS实例教程[M]．北京理工大学出版社．2002:73-80.

[5]柴晓艳，余小巧.φ406钢管端面铣头倒棱机自动送料机构的优化设计[J]. 重型机械，2010(06)：41-46.

[6]申永胜．机械原理教程[M]．清华大学出版社，1999:32-40.

[7]侯锁军,秦东晨. 基于ADAMS/View多连杆独立悬架的运动学仿真及优化设计[J]. 拖拉机与农用运输车，2010(01)：60-61.

[8]廖乐康，方扬，林新志. 齿轮齿条爬升式升船机驱动系统的电机功率计算方法[J]. 机电工程,2013(04):459-463.

[9]韩董董，王成军， 陈蕾，等. 基于ADAMS的三维并联振动铸造机的仿真与优化[J]. 铸造技术,2014(11):2721-2723.

[10]于珊珊，贺磊，郭前建. 基于ADAMS软件的机械压力机工作机构优化设计[J]. 机械设计,2013(02):24-26.

[11]王飞，杨国来，葛建立，等.某火炮射击稳定性的总体参数灵敏度分析与优化[J]. 火炮发射与控制学报，2014(04):58-61.