一种新型结晶器振动同步控制模型

·新技术新设备·

一种新型结晶器振动同步控制模型

曾晶1，胡亮2， 王文学1， 李武红1

(1.中国重型机械研究院股份公司,陕西 西安 710032；2.陕西钢铁集团有限公司科技发展部，陕西 西安 710018)

摘要：在浇铸过程中为保证铸坯在结晶器内的脱模和润滑，结晶器振动参数必须随着钢种、拉速的变化而变化。本文提出一种新型结晶器振动同步控制模型及相关振动参数的精确计算方法，取代传统的经验估计值，进一步改善铸坯表面质量。

关键词：结晶器非正弦振动；同步控制模型；负滑动时间；负滑动量；偏斜率；振幅；振频

中图分类号：TF341.6文献标识码：A

收稿日期：2015-04-18；修订日期：2015-06-10

作者简介：曾晶(1976-)，男，中国重型机械研究院股份公司高级工程师。

A new kind of synchronistic control model for MD vibration

ZENG Jing1, HU Liang2, WANG Wen-xue1, LI Wu-hong1

(1.China National Heavy Machinery Research Institute Co., Ltd., Xi’an 710032, China;

2.Shaanxi Iron & Steel(Group)Co.,Ltd.,Xi’an 710018, China)

Abstract：MD vibration parameter must be changed as steel grade & casting speed to ensure demoulding and lubrication in casting. This article puts forward a new kind of synchronistic control model using in MD vibration and give a way to calculate the vibration parameter accurately instead of estimated values by experience for improving slab surface quality more.

Keywords：MD non-sinusoidal vibration；synchronistic control model；negative sliding time；negative slip amount；vibration amplitude；vibration frequency

0前言

目前国内应用振动同步控制模型的模式大致分为正向振动模型和反向振动模型两种。所谓正向振动模型是指振动的频率随拉速的增加而增加、振幅随拉速的增加而减小，反向振动模则相反。其振动参数的控制方式如下。

α=常数

其中，f为振频，c/s；S为振幅，m；Vg为拉速，m/s；α为偏斜率，%。

这些振动参数大多依靠实际生产经验或借鉴国外相关文献中所提及的公式，并没有从振动工艺要求出发，实时、动态地计算振动参数，从而实现结晶器的同步振动控制。

至于振动模型应当采用正向振动模型还是反向振动模型，应当采用正弦振动还是非正弦振动更是众说纷纭。

本文将提出一种新型结晶器振动同步控制模型。振幅、振频与拉速的关系将不再是简单的归属于正向振动模式或是反向振动模式；偏斜率的取值不再单单依赖于经验，可以随着拉速的变化而动态改变；所有这些振动参数的确立将完全取决于振动工艺的要求。

1模型的建立

结晶器振动的目的就是使铸坯在结晶器内顺利脱模，防止结晶器铜板与铸坯发生粘结，并对拉裂的坯壳进行焊合，同时促使保护渣在结晶器内充分润滑。

由此，我们可以将结晶器的振动过程分解为上升和下降两部份。在结晶器上升的过程中，结晶器向上的速率越快则弯月面区域结晶器铜板与坯壳之间的摩擦力也就越大，初生坯壳被拉裂或拉断的几率也就越高。因此可以引入控制变量对结晶器向上振动的速率给予限定。在结晶器下降的过程中，下行的最大速率应超过拉坯速率，使得结晶器相对于铸坯发生负向滑脱，利于脱模。在负滑动的过程中，可以引入相应的控制变量对结晶器下行的动作做出限定。

对于正弦振动来说，在工艺上通常用负滑动时间、负滑动量对结晶器的振动行为进行考量。反过来，我们可以先根据生产的实际情况设定不同拉速下合理的负滑动时间、负滑动量，然后反算出振幅及振频。对于非正弦振动来说，通常使用物理意义并不直观偏斜率来控制结晶器向上振动的行为，正滑动时间、正向振动最大速率才是重要的工艺考核指标。同样，我们也可以通过设定合理的最大正向振动速率，然后反向计算出该条件下的偏斜率。

基于以上思路，可先假定结晶器的振动为正弦振动，其振动曲线方程如式(1)。

Fs(t)=S·sin(2f1·π·t)

(1)

若Fs(t)满足设定的负滑动量及负滑动时间，则可建立方程如式(2)、式(3)。

(2)

S=

(3)

式中，tn为负滑脱时间，s；f1为正弦振动振频，c/s；NSA为负滑脱量，m。

式(2)不能转换为f1关于Vs的显式表达式，但可以通过计算机得到f1精确的数值解。将f1代入式(3)可得振幅S。

在保证结晶器向下振动满足式(2)、式(3)的前提下，为进一步控制结晶器向上振动的行为，应重新建构结晶器向上振动的曲线，并保证该曲线与式(1)的下行曲线光滑连接。为保证振动加速度曲线的连续性，可在速度层面上对结晶器向上振动的曲线进行建构，如图1所示。

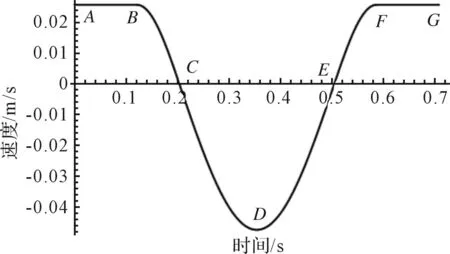
图1　非正弦振动速度曲线建构 Fig.1　Construction of non-sinusoidal velocity curve

图1所示的单个周期内的速度曲线连续、可导。曲线共分为5段。其中，“AB”、“FG”为直线段、“BC”、“EF”“CDE”为正弦或余弦曲线。由于振动的速度图像为对称图形，所以曲线“BC”、“EF”的振幅、频率一样、直线段“AB”、“FG”长度一样，且有相同的纵坐标。

设曲线“CDE”的方程为

V=2π·f1·S·cos(2π·f1·t)

(4)

其中，f1为曲线“CDE”的振频，Hz；设曲线“BC”的方程为

V=2π·f2·S2·cos(2π·f2·t)

(5)

其中，S2为曲线“BC”的振幅，m；f2为曲线“BC”的振频，c/s。

设曲线“CDE”中最大的速率为Vmax。

设曲线“AB”所对应的速率为V0=β·Vmax，0≤β≤1。

设曲线“AB”的“的长度为t0。

图1中的曲线可由结晶器正弦振动同步模型来确定其参数(振幅S、频率f1)。根据图1的图像特性和结晶器的振动固有特性可知曲线“BC”和曲线“CDE”在“C”点的斜率相同、曲线“ABC”与坐标轴所围成的面积应等于曲线“CDE”与坐标轴所围成的面积的一半。因此可建立如下方程。

(6)

求解后可得

图1所示的非正弦振动速度曲线可由参数β、f1、f2、S、S2、t0完全确定。通过计算可得非正弦振动曲线的其他相关参数。

非正弦振动曲线的频率为

(7)

非正弦振动曲线的偏斜为

(8)

偏斜率与β的关系可由图2直观的反应，偏斜率与β成反比关系，随着结晶器上升的最大速率V0越来越接近结晶器下降时的最大速率Vmax，偏斜率逐渐变小最终趋近于零。当β=1时，V0=Vmax，此时非正弦振动变为正弦振动。也就是说在本文所提到的结晶器非正弦振动同步模型涵盖了结晶器正弦振动同步控制模型，结晶器正弦振动同步控制模型只是该振动同步控制模型的一种特殊情况。

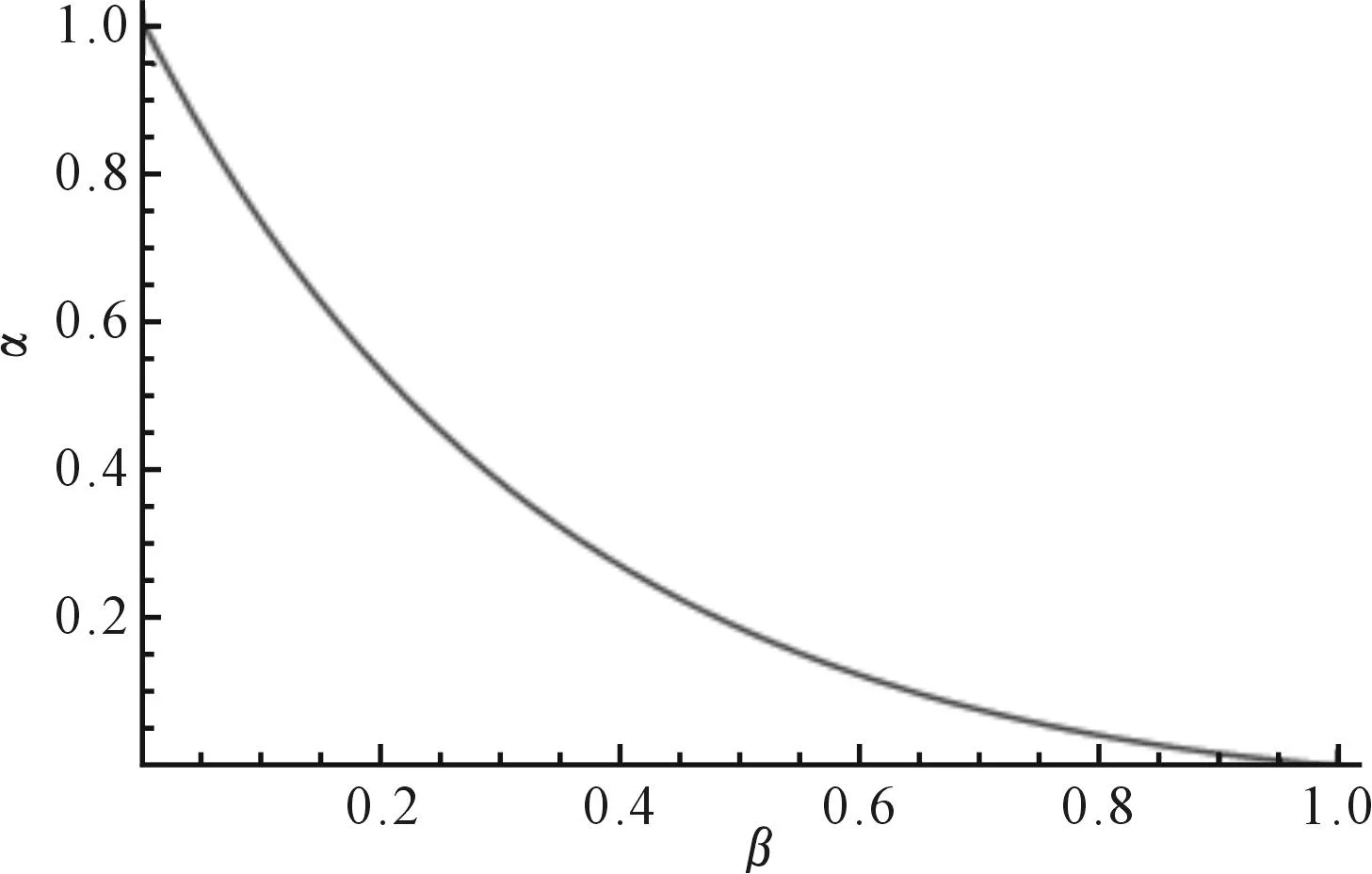
图2　偏斜率α与β的关系 Fig.2　 Relation of deflection α and β

在工程应用中，结晶器偏斜率的取值多半依赖经验，取值范围介于0%到40%。根据式(7)可知β的取值范围应当介于0.285534到1之间。也就是说在采用该结晶器非正弦振动模型行时，可将结晶器向上振动的最大速率控制在0.285534到1倍Vmax范围内。

当非正弦振动的速度曲线相关参数确定后，可得到非正弦振动的位移表达式、速度表达式和加速度表达式，分别见式(8)、式(9)、式(10)。

(9)

(10)

(11)

式(8)、式(9)、式(10)中各表达式的变量取值范围均为

2模型的应用

针对某钢种在拉速1.8 m/min的条件下，设定负滑动时间tn=0.15 s、负滑动量NSA=3.5 mm、振动的上行速率与最大下行速率的比值β=0.4，可得

α=0.26925=26.925%

S=0.004495m=4.495 mm

f=1.7011Hz=102.067 c/min

对应的单位周期内位移曲线、速度曲线、加速度曲线分别如图3、图4、图5所示。

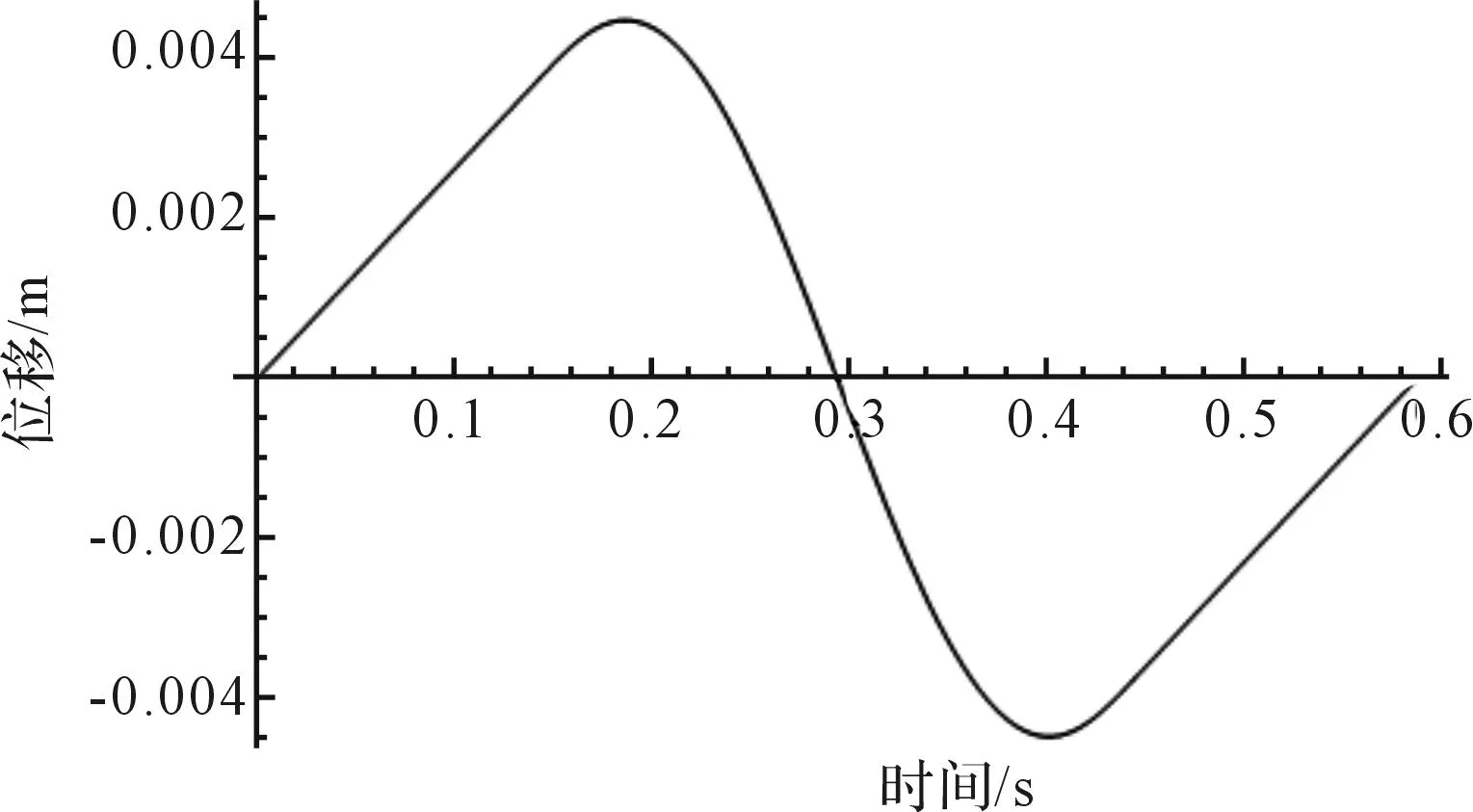
图3　位移曲线 Fig.3　Position curve

在生产过程中，拉速根据实际生产情况会发生变化，结晶器非正弦振动的振幅、频率、偏斜率也会随着拉速在实时地动态改变。我们可以根据钢种类型及该钢种的最大稳定生产拉速、按照本模型的计算方法计算出不同拉速下的非正弦振动参数，从而实现结晶器非正弦振动的同步控制。

若按表1的工艺参数要求，通过本文的同步模型计算方法我们可以得到不同拉速下的非正弦振动参数见表2。

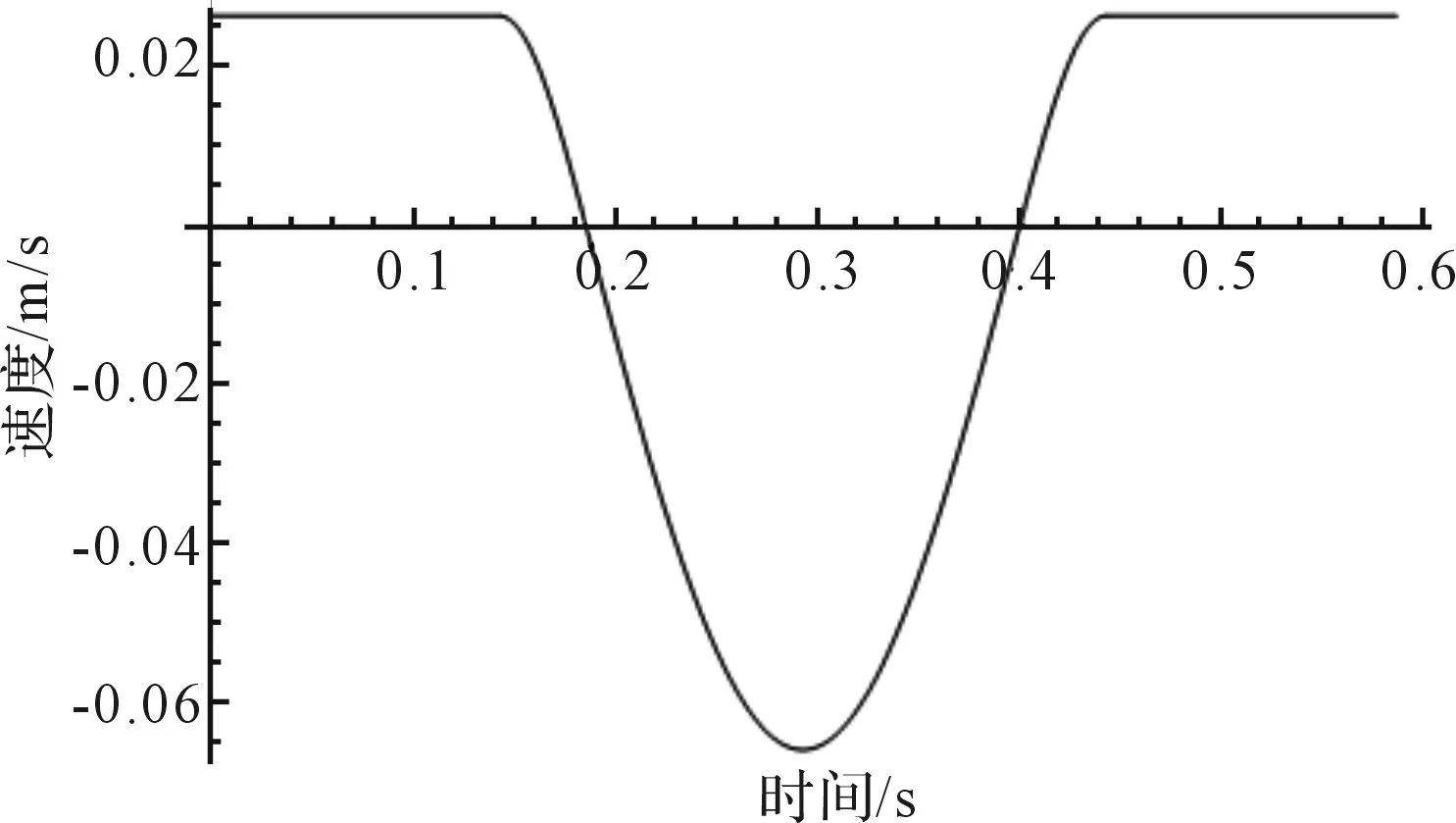
图4　速度曲线 Fig.4　Velocity curve

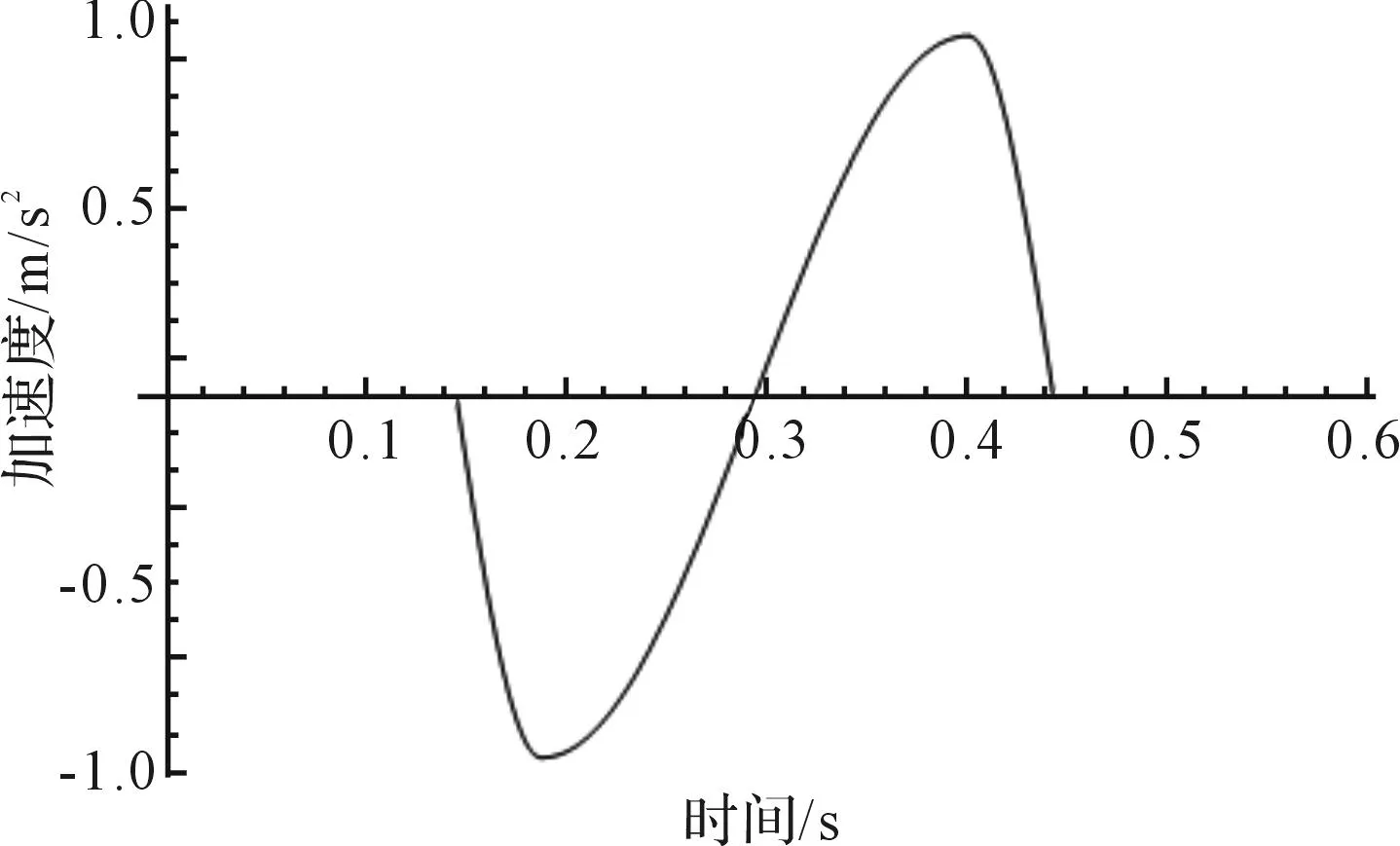
图5　加速度曲线 Fig.5　Acceleration curve

负滑动时间Tn变换范围/s0.15-0.12最高拉速Vmax/m/min1.8振动上行最大速率与下行最大速率比β1.0～0.4负滑动量NSA变换范围/mm3.5～2

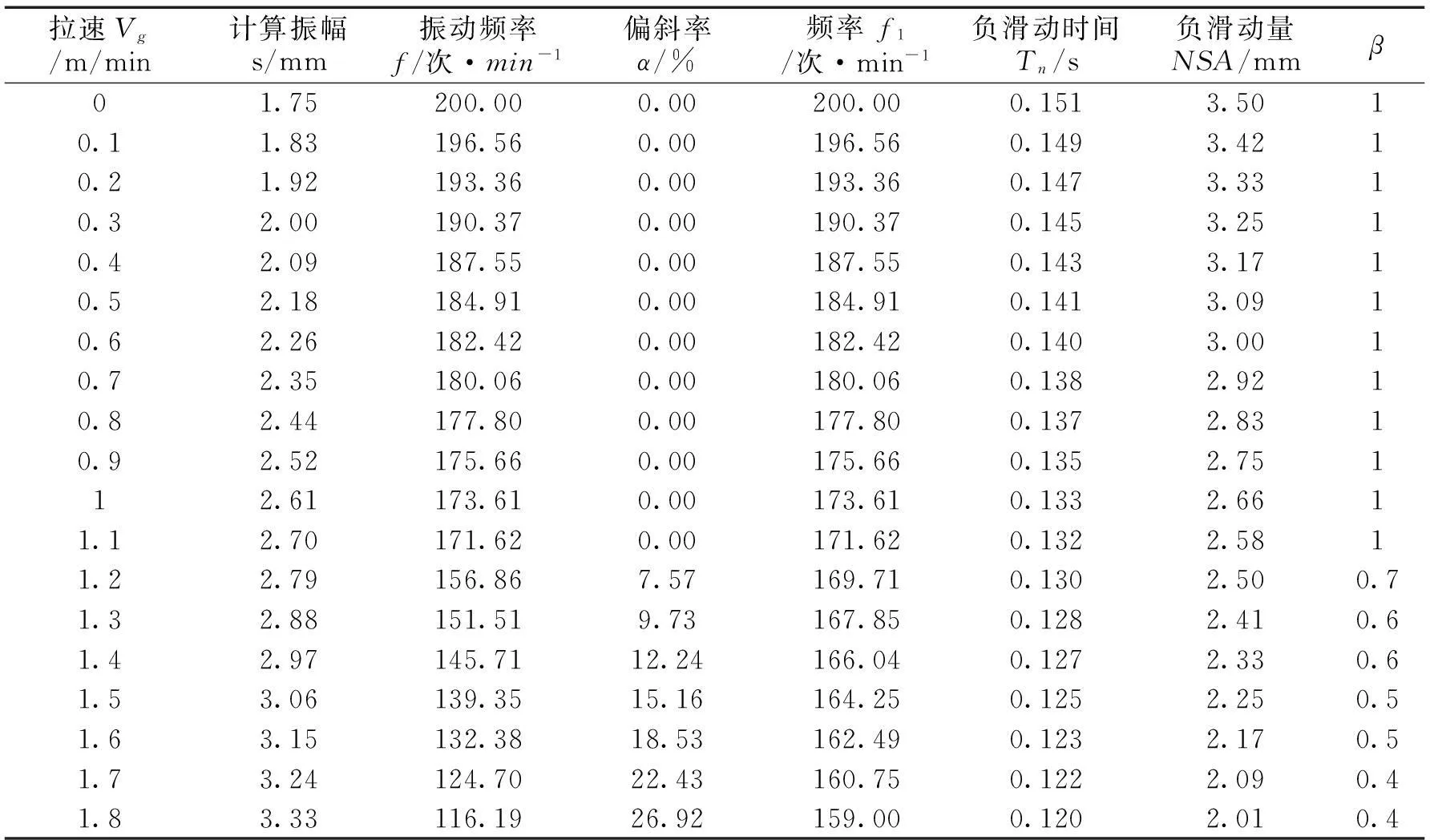
表2　不同拉速下的非正弦振动参数

3结论

本模型兼顾了正弦振动同步控制模型，即正弦振动同步控制模型仅仅是该模型的一种特殊情况，且仅当β=1时，本模型即可变为正弦振动同步控制模型。对于高拉速连铸机，甚至超高拉速连铸机，拉速的变化范围很大。当拉速处于较低的区间范围时，可以将控制变量β设定为1，将结晶器振动转化为正弦振动，可获得较大的正向滑动速度防止粘接；而当拉速处于较高的区间时，由于拉速较高，应将控制变量β设定为较低的值，以降低结晶器向上振动时相对于铸坯的速度，降低结晶器内初生坯壳被拉裂的风险。显然，结晶器非正弦振动同步控制模型比正弦振动同步控制模型有更好的适应性。同样，控制变量β随拉速的变化也可以是非线性的，这使得该模型的调整更为灵活。

参考文献:

[1]同济大学应用数学系. 高等数学(第五版). 北京[M]. 高等教育出版社,2004.

[2]蔡庆森，王小平. 连续矫直曲线的研究及应用[J]. 重型机械,2001(5).

[3]干勇等. 连续铸钢凝固过程数学物理模拟[M]. 北京: 冶金工业出版社,2001.

[4]蔡开科，潘毓淳，赵家贵.连续铸钢500问[M].北京：冶金工业出版社，1994.

[5]蔡开科. 连铸机结晶器[M].北京：冶金工业出版社，2008.