考虑环境温度的重型落地镗铣床热误差建模研究

·实验研究·

考虑环境温度的重型落地镗铣床热误差建模研究

陈学尚1,2，黄智1，许可1，衡凤琴1，王正杰1,杜丽1, 王立平1

(1.成都电子科技大学 机械电子工程学院，四川 成都 611731；2.中国燃气涡轮研究院，四川 江油 621703)

摘要：重型落地镗铣床因自身尺寸大、结构复杂且易受多热源影响导致其产生较大的热变形，使得主轴刀尖点产生偏移，降低乃至严重恶化机床加工精度。本文针对重型落地镗铣床开展了不同环境温度和工况的热特性实验，依据实验结果对常见的热误差模型进行对比分析得到了一种鲁棒性更强、预测效果好的模型，为重型落地镗铣床热误差控制提供参考依据。

关键词：重型落地镗铣床；环境温度；热误差建模；多点温度

中图分类号：TG536文献标识码：A

收稿日期：2015-06-04；修订日期：2015-07-27

基金项目：国家科技重大专项(2013ZX04013-011)

作者简介：陈学尚，男(1987-)，成都电子科技大学机械电子工程学院硕士研究生，主要研究方向为CAD/CAM。

Considering the influence of environmental temperature of heavy type milling boring machine tool thermal error modeling

CHEN Xue-shang1,2, XU Ke1, HUNG Zhi1, HENG Feng-qin1

(1.School of Mechatronics Engineering, University Electronic Science and

Technology of China, Chengdu 611731,China; 2.China Gas Turbine Establishment, Jiangyou 621703,China)

Abstract：Owing to its large structure and ranges of movement, heavy type milling boring machine is susceptible to external and internal thermal source，which will transfer to frame cause distortion. As a result of superposition of those deformations, it causes offsets to tip point and machining precision will be reduced. In this paper the thermal characteristics experiments of environment and different work conditions were conducted. According to analyze of the experiments, two kinds of usual thermal error model were compared to find which one is more robust and accurate and provide a reference for thermal error modeling.

Keywords：heavy type boring and milling machine; environment temperature；thermal error modeling; multi-point temperature

0引言

随着航天、航空、风电、船舶等方面的深入发展，对大型零部件精度要求越来越高，重型机床的应用日益受到了广泛的重视。研究表明：热误差占机床总误差的40%～70%[1]左右，已成为影响机床加工精度最主要的因素之一。为了保持及提高重型机床的加工精度，必须对机床热误差进行有效补偿，因此作为其补偿的关键支撑技术——热误差的建模研究就显得尤为重要。近年来，线性回归、神经网络理论[2-4]等也已运用到热误差建模中，由于重型机床所处的外接热源和工况的复杂性，上述研究方法对综合考虑复杂环境温度和工况共同作用情况下的热误差模型研究涉及不多，更鲜有在重型机床热误差建模规律研究中对二者的鲁棒性和预测性做出对比分析的报道。

本文主要针对重型落地镗铣床的热误差建模进行分析研究，开展了环境和不同工况下的热特性实验。通过相关实验分析，建立了新的热误差模型并与其它热误差模型对比分析，得到了一种鲁棒性更强、预测效果好的模型。

1热误差模型

由于热误差建模方法较多，首先选用了多元线性回归和BP神经网络这两种常见热误差模型进行对比分析。

1.1多元线性回归模型

多元线性回归分析是利用统计学原理建立多个输入变量和单个输出变量相对应的数学模型的技术方法。该方法具有计算量较小，计算简单，预测精度高等特点，广泛运用于热误差建模中。

以Y表示响应变量，以X1,X2,X3,…,XP表示自变量，其中P表示为自变量个数，Y与自变量之间有线性关系，二者之间的数学模型可以用以下表达式建立：

Y=β0+β1X1+β2X2+…+βPXP+ε

(1)

其中ε是随机扰动观察值，β0,β1…,βP称为回归参数或者回归系数，这些是未知参数，可以通过观测数据来估计。由式(1)表示n个随机方程的矩阵表达式为：

Y=Xβ+ε

(2)

其中β是未知参数向量，将会对它用最小二乘法进行估计。当X′X可逆时，可得：

(3)

因此观测值yi(i=1,2,…,n)的回归拟合值为：

(4)

1.2BP神经网络模型

BP 神经网络全称为 Back-Propagation Network，是一种多层前馈神经网络，即信号向前传递，误差反向传播。结构如图1所示。

图1　BP神经网络结构图 Fig.1　BP neural network structure diagram

BP神经网络模型设计如下:

(1)输入和输出层设计。输入和输出要依据求解问题和数据表现方式来确定。由于本次测量是模拟信号，以时间序列方式作为输入和输出数据方式。输出层个数由需要多少个期望来确定，输入层个数由与输出相关联个数决定。

(2)隐藏层设计。隐藏层设计包括设计几层隐含层，及确定各个隐含层神经元数目。对于 BP神经网络存在一个非常重要的定理，即对于任何在一个在闭区间连续函数都可以用含有单个隐藏层的BP网络模型逼近，因而往往只需要一个三层 BP 网络就可以完成任意维之间的映射[4]。隐藏层的神经元数目的选择是一个比较复杂的问题，很难找到一个理想的解析式来表示。目前，主要依据以下公式作为选择最佳隐藏层神经元数目时参考。

(5)

n1=log2n

(6)

式中，n为输入节点个数，m为输出节点数，n1为隐藏层节点数，a为[0,10]之间的整数。

(3)传递函数、网络学习函数、网络训练函数、性能函数的确定

2热特性实验

本次测试结合IS0230-3∶2003[5]开展了包括环境温度、常转速和变转速热误差测试，实验目的是为了测试不同环境和工况下齐二机床厂的TK6920重型落地镗铣床热关键部位的温升和机床主轴热变形。

采用电涡流传感器并基于五点法检测机床主轴热位移，运用PT100测量环境及机床温升，运用多通道数据采集卡USB2830采集数据，运用开发的软件采集温度和热变形数据。

图2　现场测视图 Fig.2　Thermal deformation and temperature rise of machine tool spindle

2.1环境温度与热变形测试

由于重型机床一般安放在普通车间，且重型机床体积大、行程长，易受车间环境温度中空气复杂流动等外界波动影响。对于普通机床来说，往往取一个环境温度测点[6，7]就足够表示环境温度信息；但是对于重型机床来说，其自身尺寸较大，所处的车间环境温度稳定性差，只用一个温度测点不足以代表实际环境温度变化的真实状态，因此有必要增加环境温度测点个数。

文献[1]指出，厂房垂直方向环境温度变化较大，而水平方向环境温度变化较小。本次选择3个环境温度测点，测试该机床不同高度温度变化。即在机床顶部安装一个温度测点T1，用以检测上端环境温度变化；主轴前端一个T11，用以检测主轴周围环境温度变化；底部一个测点T13。连续测量3天，实验结果如图2所示。

从图2分析可知，TK6920重型落地镗铣床24小时内环境温升最大可到2 ℃左右，且在同一时刻不同高度温升最大可达1 ℃。机床主轴最大热变形量可达36 μm，不容忽视，且Y、Z向变形明显大于X向。整体来看，热变形变化趋势与温度的变化趋势基本一致。

2.2不同工况下热误差实验

为了研究不同工况下机床主轴的热变形和温升规律，开展了常转速热误差实验和两种不同的变转速实验。依据前人温度测点布置经验和现场技术人员的建议，再结合TK6920重型落地镗床结构特点对整机布置温度传感器。整机共分为几个部分：滑枕部分，主轴箱部分，油膜部分，滑座，立柱部分，电机部分，环境。共布置29个温度测点，部分现场图如图3、4所示。

图2　机床冷机主轴热变形与温升 Fig.2　 Thermal deformation and temperature rise of machine tool spindle

图3　滑枕前端面温度传感器布置 Fig.3　Temperature sensor placement of ram fore-end

图4　滑枕前端上表面温度传感器布置 Fig.4　Temperature sensor placement of upper-surface for ram fore-end

不同工况下，主轴热变形如图5～9所示。

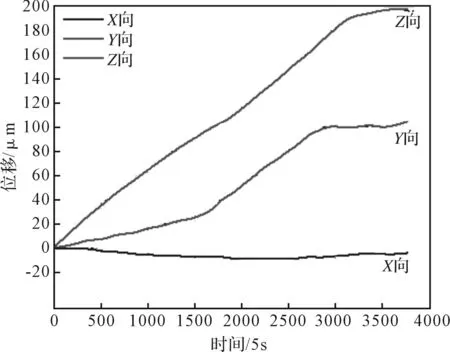
图5　恒定转速下主轴各向热误差 Fig.5　Each direction thermal error of machine-tool spindle under constant rotational speed

图6　变转速组合1主轴Z向热变形 Fig.6　 Z-direction hot deformation of spindle under variable rotational speed group 1

图7　变转速组合1主轴Y向热变形 Fig.7　Y-direction hot deformation of spindle under variable rotational speed group 1

图8　变转速组合2主轴Y向热变形 Fig.8　Y-direction hot deformation of spindle under variable rotational speed group 2

图9　变转速组合2主轴Z向热变形 Fig.9　Z-direction hot deformation of spindle under variable rotational speed group 2

常转速实验以确定机床热平衡的时间，通过不间断测量机床主轴各向热误差最长在4.5 h达到平衡，可以为机床加工前预热提供参考。不同转速下机床热变形，发现热变形的变化和转速变化大体一致，即转速变化越大，热变形变化也越大，同时指出在加工过程中应避免快速的转速变化。同时，Z向变形实验结果中均最大，而主轴X向热变形相比于Y、Z向热变形较小。因此在热误差建模过程中，重点研究Y、Z随温度变化的热误差模型。

3热误差建模

TK6920受内外热源叠加影响而产生热变形。其变形包含两部分[6，7]，即环境导致热变形和内部热源导致热变形之和，如式(7)。

Δl=Δlin+Δlext

(7)

为了描述拟合曲线的拟合效果，采用拟合率[8]指标加以判断，其中拟合率表达式如式(8)：

(8)

3.1环境对机床主轴热变形的线性回归模型

对于本次研究的对象，存在X，Y，Z向变形，由于X向变形较小，重点研究Y,Z向变形。虽然环境温度测点为3个，但是有不影响结果的测点，应该去除。以Y向为例，由于T13与Y向热变形相关系数绝对值为0.68，低于0.8按照主因素测点原则应予去掉，而T1、T11均大于0.8，分别为0.88、0.98，有必要进一步分析。以3天的环境测试数据，温升数据按照表1中温度测点组合作为输入，Y向热误差数据作为输出带入式(3)、(4)中后得到拟合输出，并将相应数据带入式(8)求得拟合率，并计算相应残差，结果见表1。

表1　环境温度测点组合结果对比

从表1中可以明显看出两个环境温度测点明显优于一个温度测点，因此环境部分测点为T1、T11即立柱顶端空气和主轴前端空气测点。Z向有相同结论，这里不再赘述。通过将组别1温度测点温升(Δt1，Δt11)数据作为输入，Y、Z向热变形数据分别作为输出导入式(3)求得系数后，将系数带入式(4)后可得环境温度与冷机下主轴热变形关系式(9)、(10)。

ΔYext=-7.3×Δt1+8.4×Δt11+0.28

(9)

ΔZext=12.43×Δt1+5.15×Δt11+5.27

(10)

3.2关键温度测点的优化选择

由于热源分为内部热源和外部热源，外部热源在本文中只考虑环境温度在上文已讨论。为了能更方便的优化内部热源温度测点个数，将按照机床结构特点和内部热源分布情况把机床温度测点分为以下五类，具体分类见表2。

表2　温度测点分类

通过变转速组合一中各个温度测点与Y、Z向相关性计算，得到相应的相关系数见表3。按照主因素策略[9，10]，将与主轴Y、Z向热变形相关系数小于0.8的温度测点去掉，余下的温度测点则按照互不相关原则优化，即每类中选取一个最具代表性的温度测点作为本类温度测点代表作为模型的输入。由于电机类所有测点没有相关系数大于0.8的温度测点，所以由原来的五类变成四类，其中每类中有只有一个温度测点作为模型的输入，结果见表4。

表3　内部热源温度测点与 Y、 Z向热变形相关系数

表4　内部热源关键点

3.3环境和内热源对主轴热变形的线性回归模型

由于该测试对象放置在一个普通车间没有环境温度控制，要想单独获得内部热源所导致的机床热误差,通过实验和测量的方式是不可能的。由于机床整体热误差是由内外部热源作用的叠加[6]，因此内部热源所导致的热误差可以通过测量得到总的热误差减去由环境温度导致的预测误差后间接得到。内部温度测点的选取已在4.2节阐述，以变转速组合1测试数据中温度测点数据T3、T2、T29、T6的温升Δt3、Δt2、Δt29、Δt6作为Y向模型输入，同样以温升Δt3、Δt22、Δt23、Δt9作为Z向模型输入，以相应的主轴Y,Z向变形数据分别作为输出带入式(3)后通过式(4)得到内部热源作用所导致热变形的模型如式(10),(11)，其中ΔYin、ΔZin单位为μm。主轴Y、Z向热变形线性回归模型拟合效果如图10和11所示。

ΔYin=0.3×Δt3+0.5×Δt2+

31.2×Δt6+9.4×Δt29

(10)

ΔZin=45.79×Δt3-12.51×Δt23-

62.99×Δt22+74.51×Δt29

(11)

图10　主轴Y向热变形线性回归模型 Fig.10　Y-direction hot deformation linear regression model of spindle

因此，集成环境和内部热源对重型机床主轴热变形的多元线性回归模型如图12,13所示。

ΔY=0.3×Δt3+0.5×Δt2+31.2×Δt6+

9.4×Δt29-7.3×Δt1+8.4×Δt11+0.28

(12)

ΔZ=45.8×Δt3+12.5×Δt23-63×Δt22+

74.5×Δt29+12.4×Δt1+5.1×Δt11+5.2

(13)

3.4BP模型

将环境温度测点和通过主因素策略和互不相关策略优化得到内部热源测点作为模型的输入，以主轴Y、Z向热变形分别作为模型的输出。模型的输入个数为6个，输出个数为1，隐藏层神经元通过式(5)(6)选定为5个。以变转速组合1中温升Δt3、Δt2、Δt29、Δt6、Δt11、Δt1作为Y向模型输入，同样以温升Δt3、Δt22、Δt23、Δt9、Δt11、Δt1作为Z向模型输入，以相应的主轴Y、Z向变形数据分别作为输出带入神经网络模型中建模。最后拟合效果如图12,13所示。

图11　主轴Z向热变形线性回归模型 Fig.11　Z-direction hot deformation linear regression model of spindle

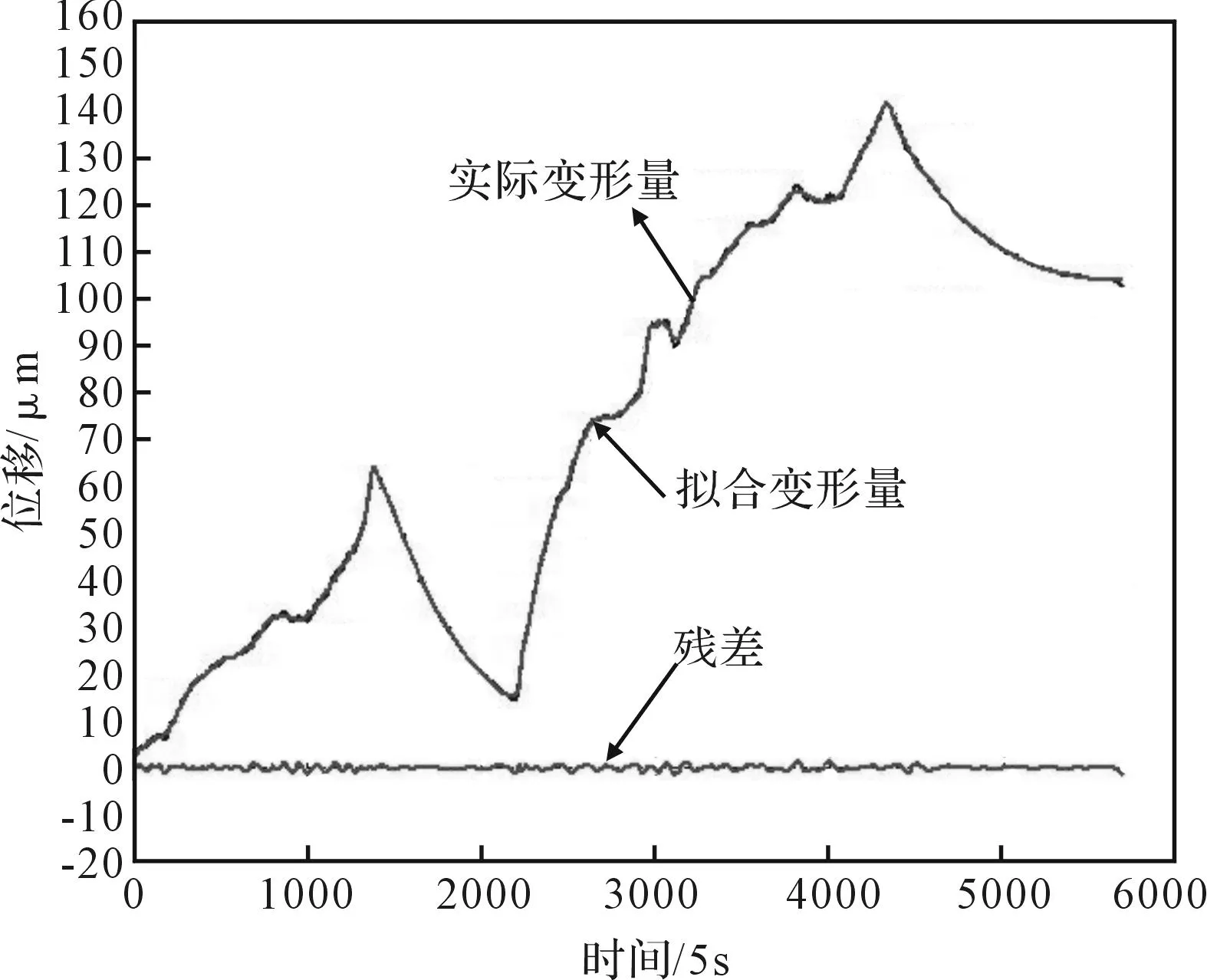
图12　主轴Y向神经网络模型 Fig.12　 Y-direction neural network model of spindle

图13　主轴Z向神经网络模型 Fig.13　Z-direction neural network model of spindle

由图12,13可以看出，神经网络模型拟合效果较好，几乎可以跟随全部实测数据拟合程度很高，分别可达96%和98%。同时对比线性回归模型和神经网络模拟合精度好于线性回归模型。

3.5模型对比分析

由于线性回归和神经网络的拟合效果都较好，为了测试模型的预测效果和鲁棒性，将选取与上述建模数据工况完全不同工况，以常转速下所获得温度测点数据作为输入，通过4.4节建立的模型计算出相应的预测值。预测结果如图14、15所示。

图14　主轴Y向模型对比 Fig.14　Contrast of Y-direction model of spindle

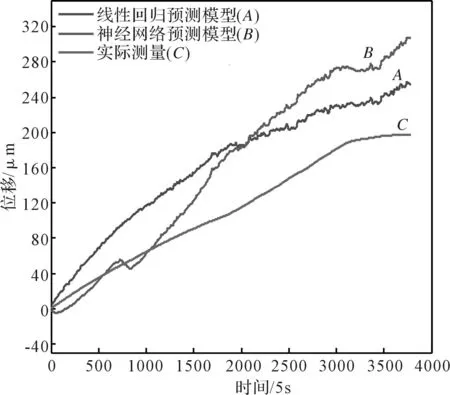
图15　主轴Z向模型对比 Fig.15　Contrast of Z-direction model of spindle

从图14分析得知，在主轴Y向热变形中，考虑到多点环境温度和内部热源相互叠加的线性回归模型与实测数据趋势大致接近，而神经网络模型失真严重；线性回归预测率为32%，神经网络预测率为8%。从图15中分析可知，线性回归模型和神经网络都与实测数据变化趋势接近，但是神经网络预测模型预测率为18%，线性回归预测模型预测率为34%。对比表明线性回归模型预测效果明显高于神经网络；另外神经网络建模还需要较多的工况数据样本，较为耗时、耗力。

4结论

本文针对重型数控落地镗铣床的热误差探讨了多元线性回归模型和BP神经网络模型建立的可行性，并结合实验建立起了考虑多点环境温度及内部热源的常用热误差模型。通过对比分析研究表明，BP神经网络和线性回归模型的拟合能力都较强，但是在考虑多点环境和内部热源共同作用下的线性回归模型的预测效果明显高于BP神经网络模型，前者具有建模简单便捷，预测精度较高，鲁棒性好的优点。本文研究成果对其它重型机床热误差模型建立具有一定的参考价值，为后续热变形控制奠定相关技术基础和理论依据。

参考文献：

[1]WECK M，MC K P． Reduction and compensation of thermal error in machine tools[J]. Annals of CIRP-CIRP Annals-Manufacturing Technology，1995，44(2) : 589-598．

[2]项伟宏,郑力,刘大成,等．机床主轴热误差建模 [J]．制造技术与机床, 2000,(11): 12-15.

[3]吴雄彪．基于贝叶斯网络的数控机床热误差建模[J]．中国机械工程, 2009, 20(3): 293-296.

[4]葛哲学,孙志强．神经网络理论与MATLAB R2007实现[M]．北京：电子工业出版社, 2007.

[5]Josef M, et al. Thermal issues in machine tools[J]. CIRP Annals-Manufacturing Technology ,2012 , 61: 771-791.

[6]林伟青，傅建中，陈子辰，等． 数控机床热误差的动态自适应加权最小二乘支持矢量机建模方法[J]． 机械工程学报，2009，45(3) : 178-182．

[7]ISO230-3:2003 test code for machine tools-Part 3: determination of thermal effects[M]. International Organization for Standardization

[8]B. Tan, et al. A thermal error model for large machine tools that considers environmental thermal hysteresis effects[J]. Int. J. Mach. Tools Manuf. 2014, 82(4): 11-20.

[9]Vyroubal J. Compensation of Machine Tool Thermal Deformation in Spindle Axis Direction Based on Decomposition Method[J].Precision Engineering,2012,36:121-127.

[10]杨建国．数控机床误差综合补偿技术及应用[D]．上海：上海交通大学,1998.

[11]E. Gomez-Acedo,A.Olarra,L.N.Lo Calle,A method for thermal characterization and modeling of large gantry-type machine tools[J].The International Journal of Advanced Manufacturing Technology 2012，62(9-12)：875-886.