改进的认知诊断模型项目功能差异检验方法——基于观察信息矩阵的Wald统计量*

刘彦楼 辛 涛, 李令青 田 伟 刘笑笑

(1北京师范大学发展心理研究所,北京 100875) (2中国基础教育质量监测协同创新中心,北京 100875)(3泰山学院教师教育学院,山东泰安 271000)

1 引言

认知诊断模型可以提供关于受测者知识或技能掌握程度的细粒度的、多维诊断性反馈信息,因此,引起了学生、教师、心理测量学家以及认知心理学家等的关注(Greeno,1980;Leighton &Gierl,2007),是当前心理测量领域研究的热点之一。迄今为止,研究者提出了许多认知诊断模型,这些模型可以被分为一般性的认知诊断模型框架以及特殊的认知诊断模型。一般性的认知诊断模型框架,主要包括von Davier (2005)的一般诊断模型(

General Diagnostic Model,

GDM)、Henson,Templin 和 Willse (2009)提出的对数线性认知诊断模型(

Log-Linear Cognitive Diagnosis Model,

LCDM)以及 de la Torre (2011)的G-DINA模型,常见的特殊的认知诊断模型有决定性输入,噪音与门模型(

Deterministic Input,Noisy And Gate,

DINA) (de la Torre &Douglas,2004;Haertel,1989;Junker &Sijtsma,2001),补偿的重参数化统一模型(

Compensatory Reparameterized Unified Model,

C-RUM) (e.g.,Hartz,2002)等。

从统计上来讲,以上这些一般性的认知诊断模型与特殊的认知诊断模型都属于有约束的潜在类别模型(von Davier,2009)。这些“约束”主要是通过Q矩阵来实现的。Q矩阵是一个设计矩阵,其中的元素一般是“0”与“1”,虽然有研究(Chen &de la Torre,2013)已经将 Q矩阵扩展为多级的,但在绝大多数的实际应用中仍假定其是二分的,因此本研究仍假定Q矩阵是二分的。在认知诊断模型中一般将受测者的知识或技能统称为潜在属性,简称属性。Q矩阵的功能在于设定认知诊断测验中项目与属性之间的对应关系,Q矩阵中元素取值为1代表正确作答某一项目需要某一对应的属性,取值为0则代表不需要。将认知诊断模型与Q矩阵在项目水平上进行组合,可以反映出研究者对于受测者在作答项目时的潜在认知过程或操作的假定。

在使用认知诊断测验对于受测者的属性掌握状况进行诊断的时候,研究者面临的一个重要的理论及现实问题是如何进行项目功能差异(

Differential Item Functioning,

DIF)检验。因为当测验中含有功能差异的项目时,不仅会产生测验公平性的问题,而且也会影响到受测者属性掌握模式的判别(王卓然,边玉芳,郭磊,2015)。在认知诊断模型中一个被广泛接受的 DIF定义是不同组中具有相同属性掌握模式的受测者正确作答某一项目的概率不同(Hou et al.,2014;Li,2008)。当前研究者们提出了一些不同的方法用于检验认知诊断模型中的DIF (Hou et al.,2014;Li,2008;王卓然,郭磊,边玉芳,2014;Li &Wang,2015;Zhang,2006)。Zhang (2006)提出使用 MH法(Holland &Thayer,1988;Mantel &Haenszel,1959)以及SIBTEST法(Shealy &Stout,1993),用受测者的测验总分以及属性掌握模式作为匹配变量去检验 DINA模型中的 DIF。Zhang (2006)所提出的方法中的不足之处在于：目标组以及对照组的项目参数以及属性掌握模式参数是作为一个整体被同时估计出来的,因此会导致其估计值不准确;另外,MH法以及SIBTEST法只能检验一致性DIF。Hou(2013)的研究中指出逻辑斯蒂克回归法(

Logistic Regression,

LR) (Swaminathan &Rogers,1990),MH法以及 SIBTEST法的统计检验力都受到测验中DIF项目比例的影响。Li (2008)使用改进的高阶DINA模型(de la Torre &Douglas,2004)去检验DIF,然而,Li研究的不足之处在于：在某些模拟条件下,经验一类错误率(指的是在实际模拟中所观察到的一类错误)过高或者过低;另外这一方法只适用于高阶模型而非一般性的模型。Hou等人(2014)提出使用 Wald统计量检验项目功能差异,并且认为Wald统计量的检验方法的效果接近或者是优于MH以及SIBTEST方法,然而,Hou等人所提出的Wald统计量存在以下不足：首先是一类错误率过高,不符合预先设置的显著性水平;其次,统计功效研究中,正确拒绝率是使用的每个模拟条件下的10,000次重复所获得统计量的经验分布来计算的,这使得其研究结果无法推广到一般性的模型以及实际应用中。另外,需要指出,Hou等人(2014)在计算Wald统计量时使用的是de la Torre (2009,2011)所提出认知诊断模型信息矩阵的计算方法。王卓然等人(2014)的研究发现尽管 Wald方法的检验力要高于LR法与MH法,但是也存在一类错误率膨胀的问题。Li和Wang (2015)比较了使用马尔可夫链蒙特卡罗(

Markov chain Monte Carlo,

MCMC)法计算项目参数时,LCDM-DIF方法以及Wald方法在评价项目功能差异时的表现。Li和Wang发现,他们所使用的LCDM-DIF方法以及Wald统计量具有较好的一类错误控制率(仅有稍许的膨胀),并且当被比较的组数为 3时,Wald统计量的统计功效要优于LCDM-DIF。

通过以上文献综述我们可以发现,尽管研究者们一致地认为Wald统计量在检验DIF时有着高的统计检验力,但是不同的研究对于 Wald统计量的一类错误控制率的表现却有着不同的结果。澄清不同的方法构建的Wald统计量为什么在一类错误控制率的表现不同这个问题,不仅在理论上具有重要意义,而且对于测验实践也有重要意义。Hou等人(2014)以及王卓然等人(2014)所使用Wald统计量,均是基于de la Torre (2009,2011)所提出的项目参数的经验交叉相乘信息矩阵而构建的,而非基于全部的模型参数(即模型中所有自由估计的参数)。然而,相关研究指出(Tian,Cai,Thissen,&Xin,2013;Paek&Cai,2013)通过对信息矩阵求逆计算误差—协方差矩阵时,信息矩阵应该包括全部的模型参数,而非仅仅是项目参数;并且研究发现当模型的参数是通过EM (Expectation-Maximization)方法(de la Torre,2009,2011)所估计获得时,应该通过对观察信息矩阵(基于样本观测数据所计算的信息矩阵,有些研究中也将其简称为观察矩阵)求逆的方法计算误差—协方差矩阵(Kenward &Molenberghs,1998;Louis,1982)。已有研究发现在项目反应理论中观察信息矩阵的逆可以很好的渐近误差—协方差矩阵(Paek &Cai,2013)。

针对以往研究中Wald统计量构建方法的局限,解决在认知诊断模型中更加准确地估计Wald统计量这一重大理论问题,促进认知诊断测验在实践中的运用,本研究拟将观察信息矩阵的计算方法引入到认知诊断模型中,期望获得一个好的误差—协方差矩阵的估计方法,从而改进 Wald统计量在检验DIF时的表现。研究包括主要包括以下3个部分：首先,介绍用于检验认知诊断模型中 DIF的 Wald统计量的构建,重点强调误差—协方差矩阵在构建中所起的重要作用;其次,介绍认知诊断模型中经验交叉相乘信息矩阵以及观察信息矩阵的计算方法;第三,采用模拟的方法,探索本研究所提出的改进后的Wald统计量在计算DIF时的一类错误控制率以及统计检验力的表现,并且与通过经验交叉相乘信息矩阵而构建的Wald统计量所获得的结果进行比较;为了更好的说明本研究中的研究结果,我们也将本研究的结果与其他采用相同实验设计的研究的结果(如,Hou et al.,2014;Li &Wang,2015)进行了直接的比较。

2 改进的Wald统计量的计算方法

在本研究中,我们将使用LCDM作为例子,说明在认知诊断模型中如何应用改进后的Wald统计量进行DIF检验。LCDM是一个广义的认知诊断模型,对于其中的参数进行约束,便可以获得一些特殊的模型,如DINA以及C-RUM等(Henson et al.,2009)。

LCDM 假定在给定属性掌握模式α的条件下,受测者

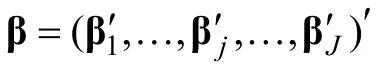
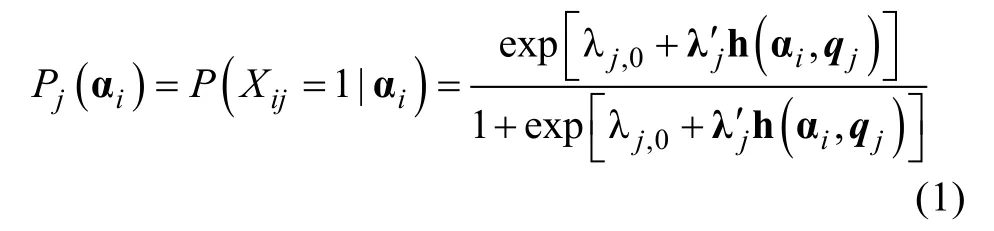
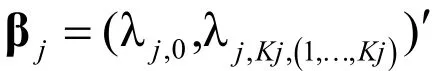
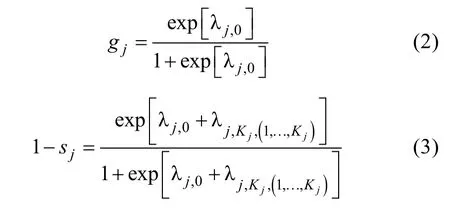
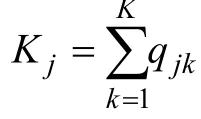
i

在各个项目上的作答是独立的,其反应向量X的似然函数,可以表示如下,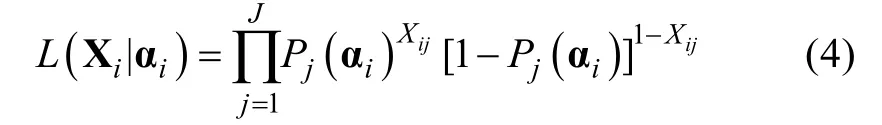

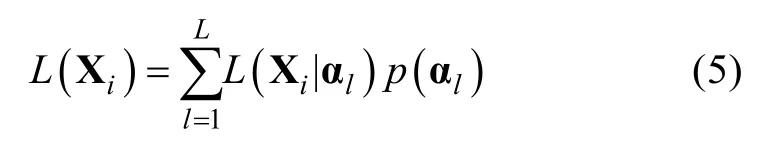
反应向量X的边际概率,可以表示为：

在公式(5)中,

p

（α）是属性掌握模式 α的概率,在LCDM中,所有属性掌握模式的概率之和为1。为满足这一约束,本研究参考 Rupp,Templin和 Henson(2010)所使用的概念,设η=(η,…,η)′为模型的结构参数(

structural parameters

),用以描述任一受测者来自特定属性掌握模式的概率,使用以下表达式,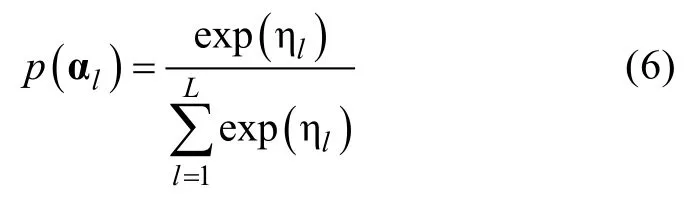

并且对结构参数η施加约束,固定其中任一参数为0,一般而言,可以选择固定最后一个模型参数η为0。

再进一步假定,受测者之间的作答都是独立的,因此所有受测者作答X的似然函数为可以用如下公式来表示,

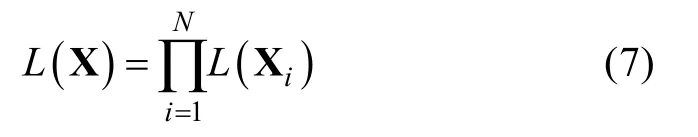
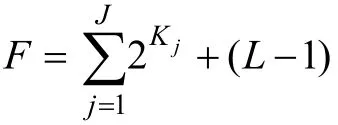
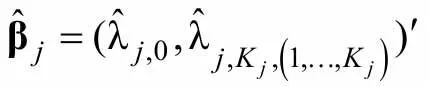
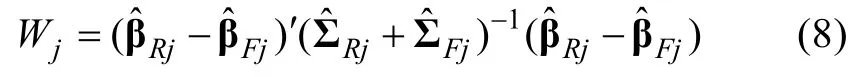
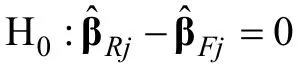
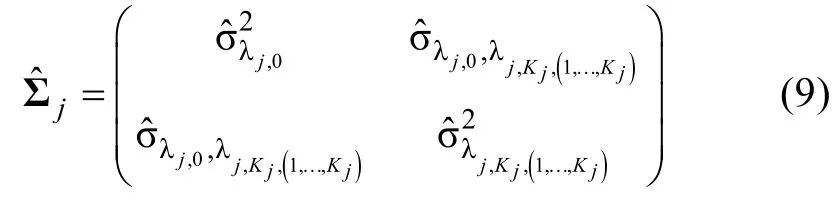
从公式(8)可以发现方差—协方差矩阵估计的准确性,对于 Wald统计量会产生重大的影响,这也就是说LCDM中信息矩阵的估计会对Wald统计量的计算产生重大影响。

EM算法(Dempster,Laird,&Rubin,1977)对于心理测量学产生了非常大的影响,它将复杂的计算非完整数据似然函数最大值问题转换为较为简单的一系列伪完整数据问题,在认知诊断模型分析软件中得到了广泛的应用。然而,在通过EM算法计算参数时,信息矩阵(或者是其逆方差—协方差矩阵)并不是伴随产生的,因此,需要去进行专门的计算。研究发现,当使用期望—最大化算法去计算模型的极大似然估计值时,使用观察信息矩阵能够很好的去渐近模型的方差—协方差矩阵(Louis,1982),感兴趣的研究者可以参考 Kenward和 Molenberghs(1998)的研究。对于 LCDM 而言,包含所有自由估计参数的经验交叉相乘信息矩阵的公式可以表达如下：

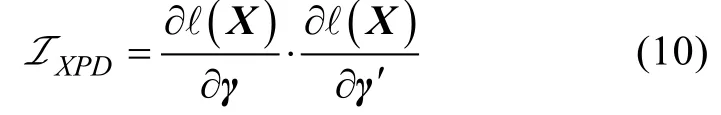
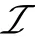
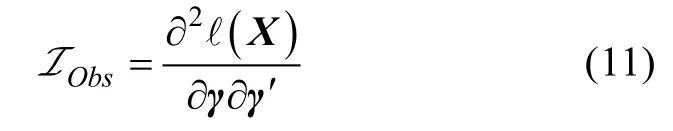
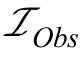
3 方法

3.1 研究设计

采用 Monte Carlo的方法进行研究,受测者的作答反应、模型的参数估计以及Wald统计量的计算均采用

R

语言(R Core Team,2015)编程实现。每种实验条件均重复1000次,以获得稳定的结果。为了便于与以往研究结果进行直接的比较,本研究所采用Hou等人(2014)所设计的实验条件,这些实验条件也被Li和Wang (2015)所采用。与Hou等人(2014)研究不同的是,本研究中 Wald统计量的计算是通过包含全部模型参数的观察信息矩阵或者是经验交叉相乘信息矩阵所计算获得的。

本研究中所采用Q矩阵中包含30个测验项目,5个属性,并且限制每个项目所包含的属性数量最多为3。Q矩阵采用平衡设计,每个属性被项目所测量的次数相等,同样使包含 1、2、3个属性的项目数量也相等即包含1、2、3个属性的项目分别有10个。具体的Q矩阵设计见表1。

为方便与以往研究结果进行直接对比,本研究设计中的数据生成模型也同样采用DINA模型,对照组中的猜测以及滑动参数设置为相等,且有三个水平：0.1,0.2以及0.3,猜测以及滑动参数值设置的越小,说明项目越能够区分出受测者是否掌握了所测的属性(Templin &Henson,2006)。DIF类型有两个水平：一致性DIF以及非一致性 DIF。一致性 DIF指的是对于某一个组而言,正确作答某个项目的概率在所有可能的属性掌握模式下均一致性地高或者是低;非一致性DIF指的是正确作答某个项目的概率在一些属性掌握模式下高,在另外一些属性掌握模式下低,或者是相反,即正确作答的概率具有非一致性。DIF大小有两个水平：0.05与0.1,当项目参数值为0.1时仅考虑了0.05这一水平的DIF大小,以防项目参数值等于 0。样本大小有两个水平：500与1000。在认知诊断模型中样本的大小会对模型参数估计值的精确性产生影响,进而也会影响到Wald统计量的计算,因此,样本大小也是一个需要考虑的重要因素。

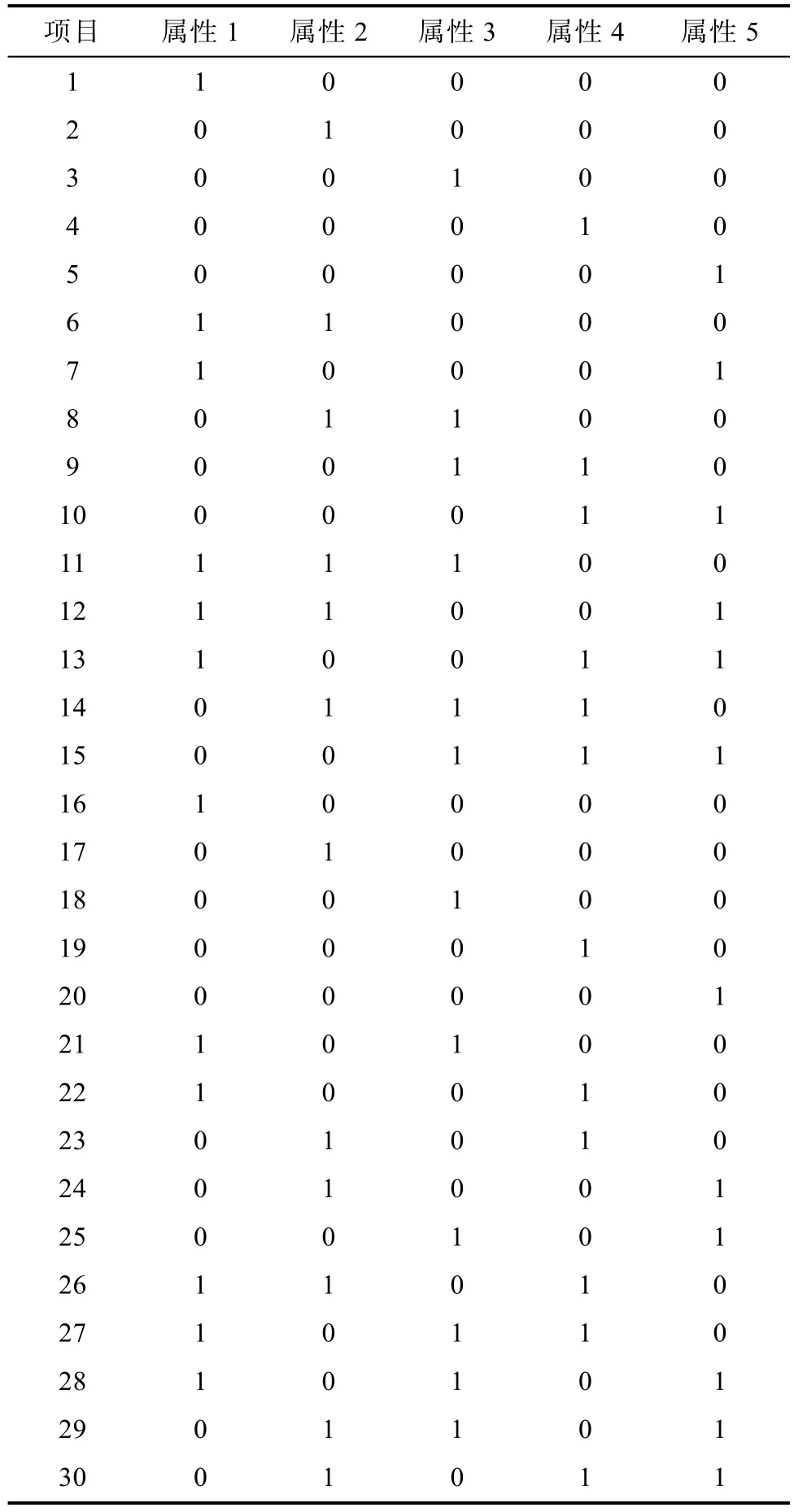
表1 Q矩阵

3.2 评价指标

本研究中所采用的评价指标为经验一类错误率以及统计检验力。经验一类错误率是通过 1000次模拟中,错误地检验出每个项目出现DIF的百分比,然后参照以往研究结果的呈现方式(Hou et al.,2014),分别对包含一个、两个以及三个属性的项目求平均。统计检验力指的是在这1000次循环中正确拒绝原假设的比例。当认知诊断测验中不存在 DIF时,如果我们所构建 Wald统计量是渐近卡方分布的,那么它观察到的一类错误率应该符合预先设置的理论上的一类错误控制率,如0.05;如果在认知诊断测验中存在 DIF,那么 Wald统计量正确拒绝的比例越高,说明它能够检验出DIF项目的能力越强。

4 研究结果

4.1 经验一类错误率

表2呈现了各个实验条件下的使用观察信息矩阵估计方法的Wald统计量获得的平均经验一类错误率。计算一类错误控制率所使用的参照分布为自由度为2的卡方分布。通过表2可以发现当项目的猜测以及滑动参数都比较小的时候,即项目能够较为有效的区分受测者是否掌握所测属性的时,一类错误控制率能够很好的接近预先设置的显著性水平。随着样本量的增大,一类错误控制率的表现也越好。另外,不论是包含一个、两个还是三个属性的项目,其观察一类错误率均能较好的接近0.05这一显著性水平。另外需要指出的是,尽管在当样本量较小(

N

=500)且项目的猜测参数以及滑动参数较大的情况下(

g

=

s

=0.3),平均的经验一类错误率表现较差,但根据 Bradley (1978)的健壮宽松准则(当显著性水平为 0.05时经验一类错误控制率在0.025与 0.075之间),仍然可以认为是得到了较好的控制。可以发现,本研究中所提出的改进的Wald统计量计算方法所获得的结果并不存在过度膨胀的现象,这与 Hou等人(2014)以及王卓然等人(2015)的结果恰好相反,说明本研究中所提出的Wald统计量的计算方法明显优于以上两个研究所使用的 Wald统计量的计算方法。通过比较表2与表3中的一类错误控制率可以发现基于观察信息矩阵计算的Wald统计量的表现要优于基于经验交叉相乘信息矩阵而计算的Wald统计量。基于经验交叉相乘矩阵而获得的Wald统计量的一类错误控制率较为保守,但是表3的结果同样显示包含一个、两个以及三个属性的项目的一类错误控制率仍大致相等。Li和 Wang (2015)在 MCMC框架下采用LCDM-DIF以及Wald统计量对于DIF检验方法进行了研究,在其研究一中同样采用了 Hou等人(2014)的研究设计,因此本研究的研究结果同样也是可以直接与 Li等人的结果进行比较。通过对比研究结果可以发现,本研究中所提出基于观察信息矩阵计算的Wald统计量与Li等人的研究中所使用的LCDM-DIF以及Wald统计量均具有较好的一类错误控制率。一个非常有意思的现象是在本研究中的一些实验条件下(见表2)Wald统计量一类错误率有细微的保守而Li等人研究结果中的LCDM-DIF以及 Wald统计量在某些实验条件中一类错误率却有稍许膨胀。从公式(8)中可以发现Wald统计量的准确性,依赖于模型参数估计值的准确性。当受测者数量较少(如

N

=500时)或者是模型中的“噪音”过大时(如项目的猜测与滑动参数均为 0.3时),模型参数估计值的准确性会受到相对较大的影响,因此,在本研究的

N

=500以及

g

=

s

=0.3这两种条件下Wald统计量一类错误率有细微的保守。

表2 基于观察信息矩阵的平均的经验一类错误率(α=0.05)

表3 基于经验交叉相乘信息矩阵的平均的经验一类错误率(α=0.05)

4.2 统计检验力

表4中呈现的是当认知诊断测验中存在一致性DIF时的考察一个、两个以及三个属性项目在1000次循环中的基于观察信息矩阵计算的 Wald统计量的平均经验拒绝比例,所使用的参照分布同样为自由度为2的卡方分布。从表4中可以看出,随着DIF的增大,Wald统计量的统计检验力也会随之增大,并且当项目的猜测以及滑动参数都为 0.2的时候,总平均的拒绝率要大于同为0.3时的项目参数值的条件。这是由于同项目参数值0.3相比,DIF大小为0.1时,这一值对于项目参数值0.2而言相对更大。随着样本量的增加,Wald统计量的统计检验力也在变大,即样本量的大小对用于检验DIF的Wald统计量而言也是一个重要因素。因为随着样本量的增加,模型参数估计值的准确性也会增加,进而会使得参数估计值的标准误变小,因此,在对照组与目标组项目参数差异相等的情况下,更倾向于获得一个大的Wald统计量的值。另外,通过观察平均值可以发现,当目标组具有负向的 DIF时,同正向 DIF相比,Wald统计量的统计检验力更大。比较表4与表5,可以发现基于观察信息矩阵的Wald统计量的统计检验力均要明显优于基于经验交叉相乘信息矩阵的Wald统计量的统计检验力。这也说明基于经验交叉相乘信息矩阵的Wald统计量存在保守的问题。

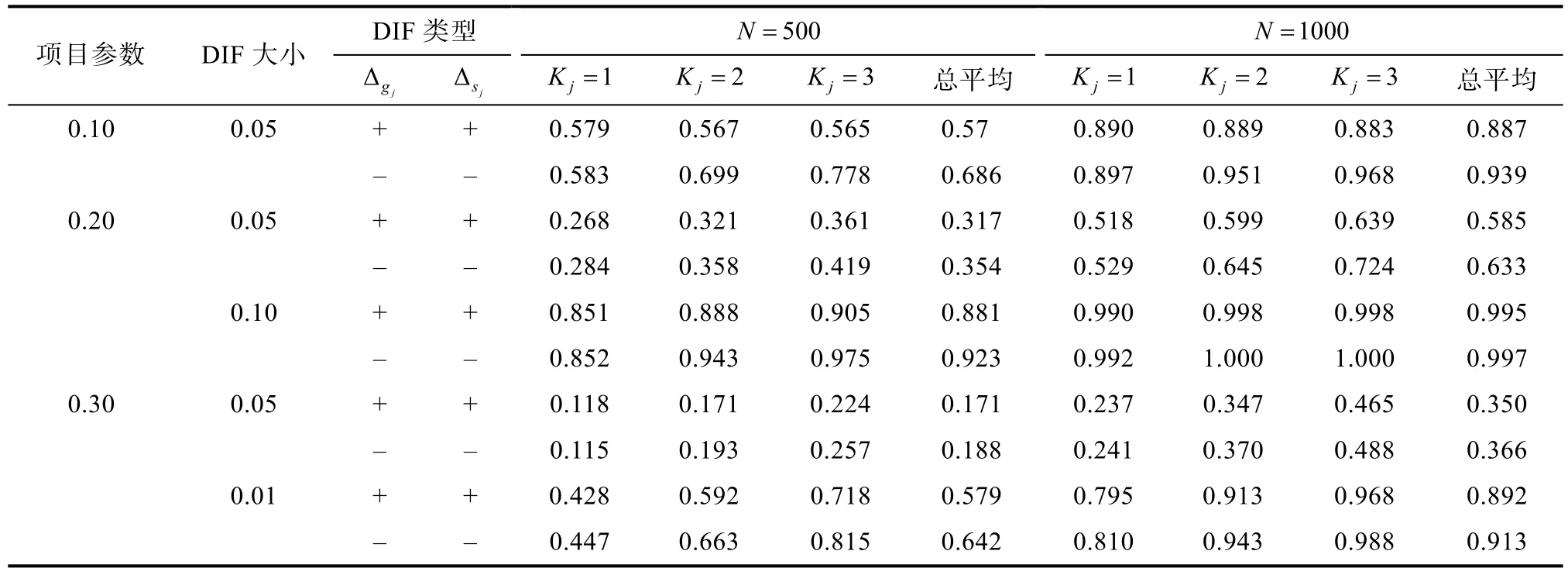
表4 基于观察信息矩阵的一致性DIF的平均经验统计检验力(α=0.05)

表6中呈现的是非一致性DIF条件下采用观察信息矩阵的Wald统计量的1000次模拟结果,计算统计检验力所使用的参照分布同样为自由度为2的卡方分布。从表6中同样可以发现随着DIF的增大,Wald统计量的统计检验力也在增大。随着样本量的增加,Wald统计量的统计检验力同样是在增大的。而且在DIF大小相同条件下,当项目的猜测以及滑动参数相对较小时,Wald统计量的统计检验力会相对较大。比较表6与表7同样可以发现,在非一致性DIF条件下,采用观察信息矩阵计算的Wald统计量的统计检验力均高于采用经验交叉相乘信息矩阵而计算获得的Wald统计量的统计检验力。

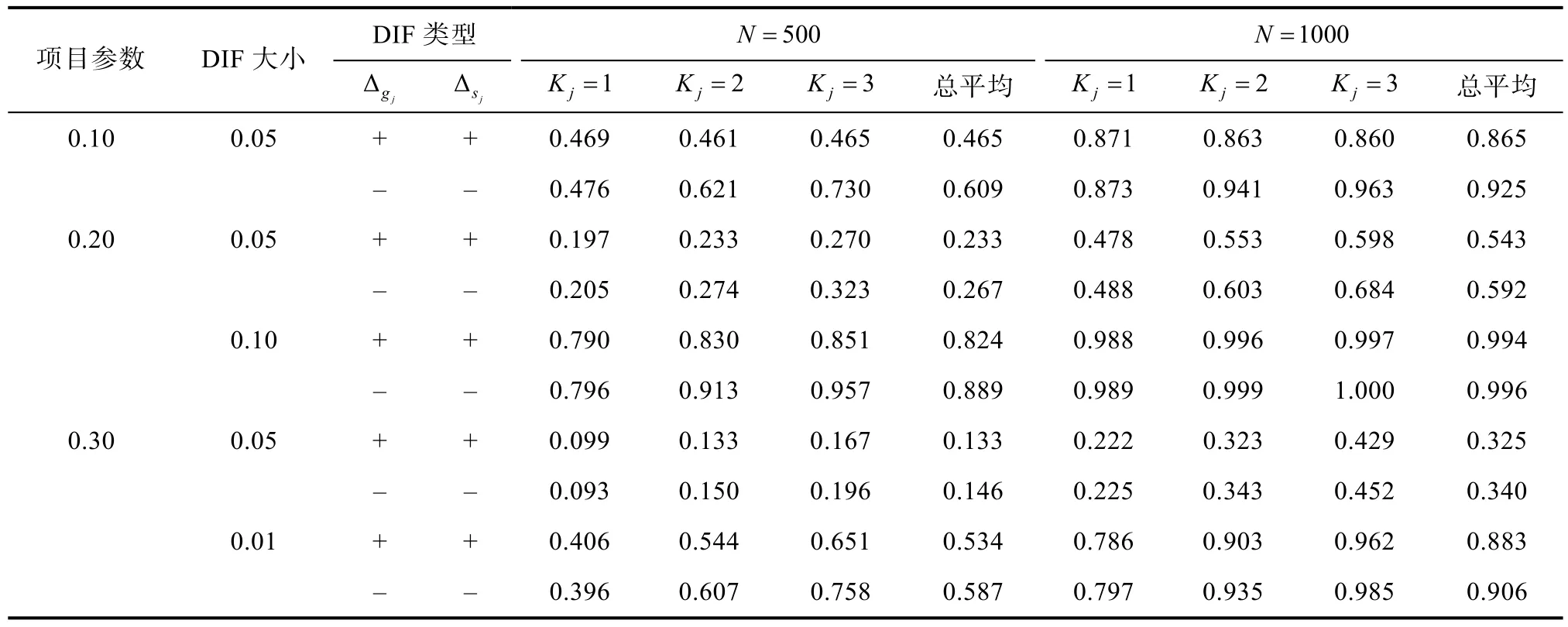
表5 基于经验交叉相乘信息矩阵的一致性DIF的平均经验统计检验力(α=0.05)

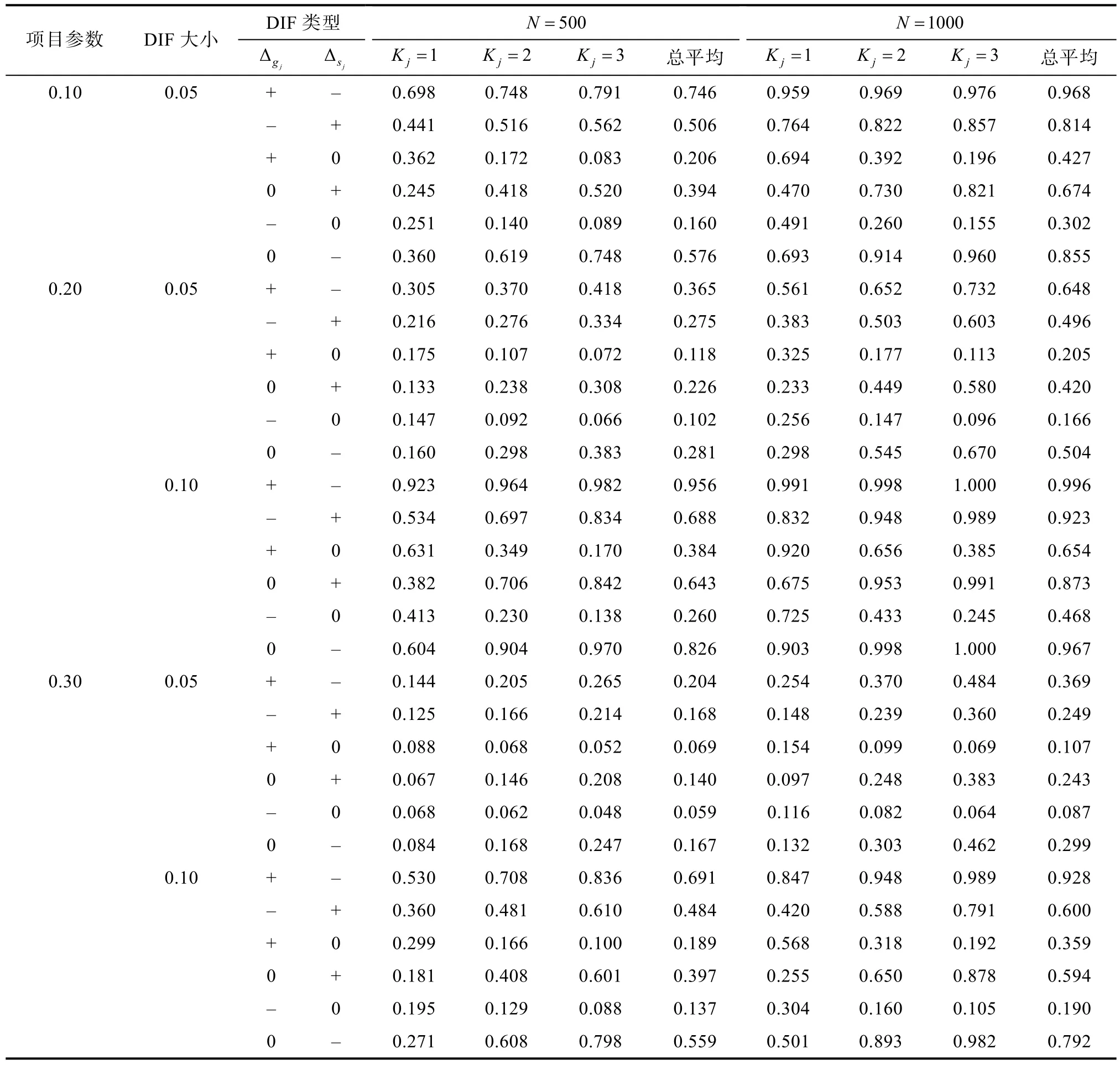
表6 基于观察信息矩阵的非一致性DIF的平均经验统计检验力(α=0.05)

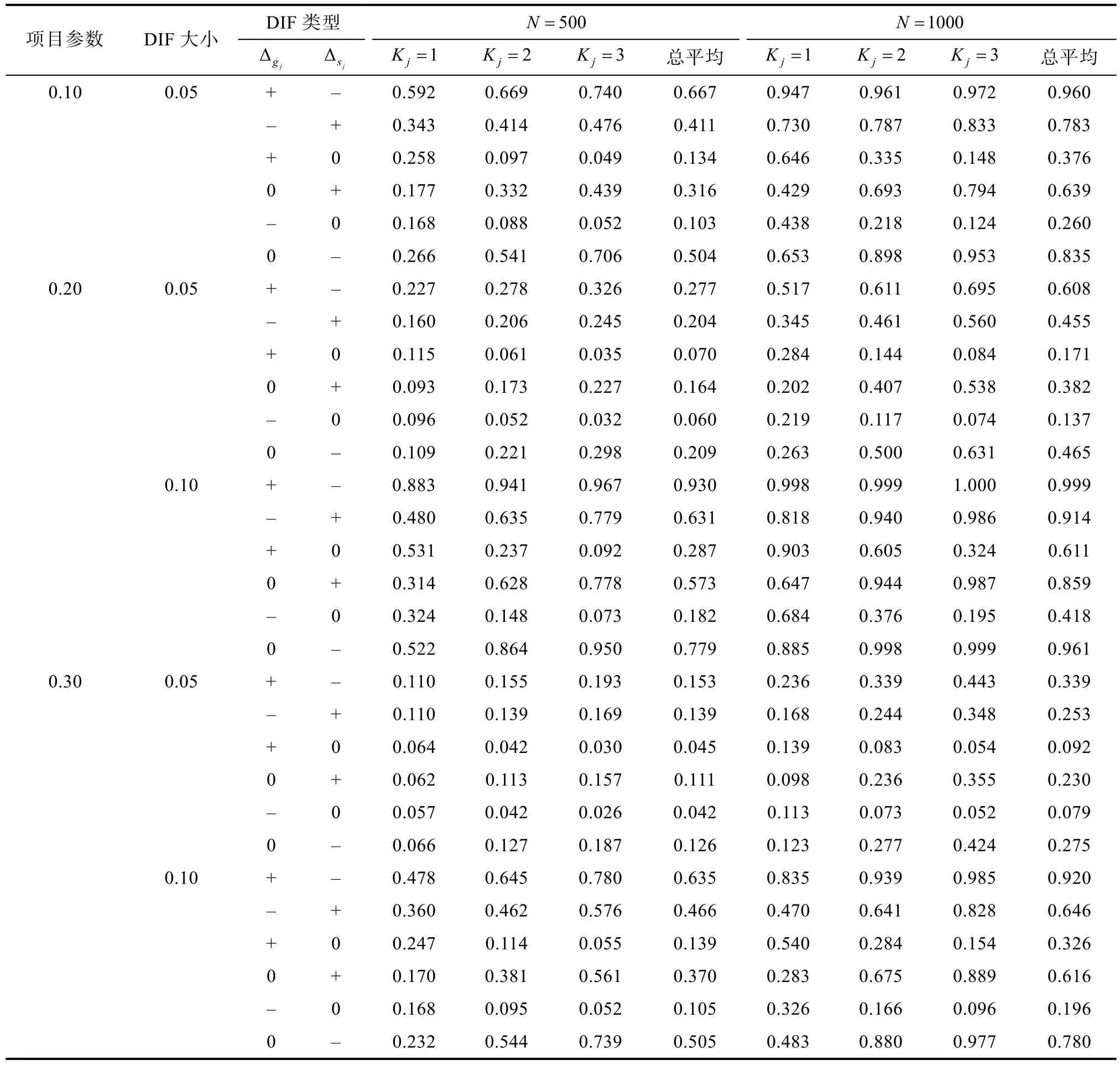
表7 基于经验交叉相乘信息矩阵的非一致性DIF的平均经验统计检验力(α=0.05)

5 讨论

认知诊断模型能够提够关于受测者属性掌握模式的较为详尽的诊断性信息,它不仅能为老师的教以及学生的学提供有针对性的建议,而且也有助于教育者深入理解受测者的认知心理。在使用这一模型来解释受测者的作答之前,研究者需要确定认知诊断测验项目的参数对于所有受测者都是不变的,否则会对受测者的属性掌握模式的估计带来不良的影响(王卓然等,2015),进而导致错误的诊断性信息。DIF检验可以用以确认不同组的受测者在同一个项目的作答上是否存在差异,即除了属性掌握模式外,受测者所在的组会影响到他们对于项目的反应。为保证测验的效度,在使用认知诊断模型来拟合受测者的作答数据前,需要进行DIF检验。先前研究者发现Wald统计量在检验DIF时,有着许多其他统计量所不具备的优点,然而前人研究中对于Wald统计量在检验DIF时的一类错误率的表现,存在明显的结论冲突。如,Hou等人(2014)以及王卓然等人(2014)的模拟研究发现 Wald统计量会存在一类错误控制率膨胀的问题,Li和Wang (2015)的模拟研究却发现,其研究中所用的 LCDM-DIF以及Wald统计量在使用MCMC计算时有着良好的一类错误控制率。本研究采用Hou等人以及Li等人研究中所使用的同等条件通过模拟发现,这些差异主要是由于 Wald统计量计算方法的差异引起的。因此,我们认为本研究提出的改进的 Wald统计量的计算方法解决了 DIF研究中一直困扰研究者的Wald统计量在检验DIF时的一类错误率的表现不同这一重要问题,具有重大的理论意义。

5.1 Wald统计量在检验DIF时的一类错误控制率

在模型正确设定的前提下,如果统计量能够很好的服从渐近分布,那么,它的一类错误控制率应该能够较好的接近预先设定好的显著性水平。本研究中所提出改进的 Wald统计量的计算方法具有这一特征,从结果中可以发现,本研究的一类错误控制率均较好地接近预先设定的 0.05这一显著性水平。因此,我们认为在Hou等人(2014)以及王卓然等人(2014)研究中所产生的 Wald统计量一类错误膨胀的问题,是由于不恰当的信息矩阵估计方法而引起的。本研究的这一结果明确地解释了为什么 Wald统计量在不同研究中有不同表现的问题,对于认知诊断模型的理论发展有一定的推动作用。另外,相对于MCMC参数估计方法,MMLE/EM具有运算量小、耗时短等优点,本研究所提出的改进的 Wald统计量正是基于 MMLE/EM,因此,本研究不仅具有重大的理论意义,而且对于认知诊断实践也具有重要的现实意义。

5.2 Wald统计量在检验DIF时的统计检验力

当确认统计量的一类错误控制率能够较好的接近预先设定的显著性水平后,接下来所要考虑的另外一个重要问题是当认知诊断测验中的项目中存在 DIF时,这一统计量能否有效地拒绝不存在DIF的原假设而选择备择假设。通过表4与表6中的结果,可以发现在样本量较大时(

N

=1000),改进后的Wald统计量在检验DIF时的统计检验力均明显的高于样本量比较小时(

N

=500)的统计检验力。因此,本研究建议在应用Wald统计量进行DIF检验的时候,如果想要达到较高的统计检验力,应保证较大的样本量。因为Hou等人(2014)发现,其研究中所采用的 Wald统计量计算方式,会导致一类错误率膨胀,因此,在计算统计检验力的时候,她们采用了两种方式进行。第一种方式是直接用 Wald统计量的理论分布即自由度为2的卡方分布的理论值来计算,由于其开发的 Wald统计量的计算方式的一类错误率膨胀会使得原本不存在 DIF的项目被误判为存在 DIF,因此计算结果不够可靠;她们所采用的第二种方式是计算当不存在 DIF项目时Wald统计量在每种实验条件组合下10,000次模拟的经验分布,然后通过获得的显著性水平的临界值,来计算Wald统计量的统计检验力,这种计算方式虽然保证了模拟实验结果具有较高的可靠性,但是不具备现实的可操作性,因此,对于其研究目的而言只能算是一种不完整解决的方案。因为Hou等人(2014)的第二种计算方式具有较高的理论上的结果可靠性,因此可以作为研究结果的一个参考。通过研究结果对照我们发现,本研究所采用的自由度为2的卡方分布理论值所计算获得的研究结果与 Hou等人(2014)的第二种计算方式所获结果具有很高的一致性,这也能够间接的表明,本研究所使用的改进后的Wald统计量计算方式具有准确性及可靠性的特点。

5.3 以后的研究方向

由于本研究关注的重点在于,在EM算法框架下提出一个恰当的 Wald统计量的计算方式,用以准确有效地来检验认知诊断测验中可能存在的DIF项目,澄清以往研究中所用de la Torre (2009,2011)所提出的信息矩阵方法计算Wald统计量时所产生的令人困惑的结果。因此,本研究仅采用了Hou等人(2014)的研究设计,通过结果对比的方式来证明本研究所提出的改进的Wald统计量在检验DIF时具有准确性可靠性等特点。具体而言,研究者可以就以下几方面进行后续研究：首先,样本大小对于 Wald统计量有重要影响,因此,后续研究中可以使用本研究中所用Wald统计量考察这一因素对于DIF的影响;其次,目前的研究中普遍采用 DINA或者是高阶DINA作为例证模型,本研究出于结果比较的因素考虑,也是以DINA模型为例,在其他认知诊断模型中Wald统计量用以检验DIF时的表现,也是一个非常有意思的研究方向。由于本研究所采用的是对于LCDM模型进行约束而获得的DINA模型,因此,可以很方便的进行扩展;第三,本研究所采用的项目数量为 30,且受测者组的数量为 2,在不同项目数量下以及不同的受测者组数量数下,Wald统计量的表现也值得研究者关注;第四,在认知诊断模型中,除了Wald统计量可以进行DIF检验之外,还有一些其他的统计量也可以进行 DIF检验(Li,2008;Sünbül &Sünbül,2015,July),虽然目前研究表明,Wald统计量在检验DIF时,具有一些其他统计量所不具有的优点,但是,在另外的应用情景中,这些DIF检验方法的优缺点,仍然值得研究者的关注。

6 结论

本研究中所提出的改进的 Wald统计量的计算方法,在认知诊断测验中不存在DIF项目时,有着良好的一类错误控制率,能够较为准确地接近预先设定的显著性水平,即当认知诊断模型为DINA时,改进的Wald统计量服从自由度为2的卡方分布;在认知诊断测验中存在DIF时,改进的Wald统计量能够准确有效的鉴别出存在DIF的项目。本研究同样发现样本量对于 Wald统计量的一类错误控制率及统计检验力存在重要影响。另外,我们建议认知诊断模型的研究者与使用者,当采用EM算法进行参数估计时,在确认认知诊断模型正确设定后,使用本研究中所使用观察信息矩阵的方法计算项目参数的标准误。

Bradley J.V.(1978).Robustness?.

British Journal of Mathematical and Statistical Psychology,31

,144-152.Chen,J.S.,&de la Torre,J.(2013).A general cognitive diagnosis model for expert-defined polytomous attributes.

Applied Psychological Measurement,37

,419-437.de la Torre,J.(2009).DINA model and parameter estimation：A didactic.

Journal of Educational and Behavioral Statistics,34

,115-130.de la Torre,J.(2011).The generalized DINA model framework.

Psychometrika,76

,179-199.de la Torre,J.,&Douglas,J.A.(2004).Higher-order latent trait models for cognitive diagnosis.

Psychometrika,69

,333-353.Dempster,A.P.,Laird,N.M.,&Rubin,D.B.(1977).Maximum likelihood estimation from incomplete data via the EM algorithm.

Journal of the Royal Statistical Society,Series B,39

,1-38.Greeno,J.G.(1980).Trends in the theory of knowledge for problem solving.In D.T.Tuma &F.Reif (Eds.),

Problem solving and education: Issues in teaching and research

(pp.9-23).Hillsdale,NJ：Erlbaum.Haertel,E.H.(1989).Using restricted latent class models to map the skill structure of achievement items.

Journal of Educational Measurement,26

,301-321.Hartz,S.M.(2002).

A Bayesian framework for the unified model for assessing cognitive abilities: Blending theory with practicality

(Unpublished doctorial dissertation).Department of Statistics,University of Illinois at Urbana-Champaign.Henson,R.A.,Templin,J.L.,&Willse,J.T.(2009).Defining a family of cognitive diagnosis models using log-linear models with latent variables.

Psychometrika,74

,191-210.Holland,P.W.,&Thayer,D.T.(1988).Differential item functioning and the Mantel-Haenszel procedure.In H.Wainer &H.I.Braun (Eds.),

Test validity

(pp.129-145).Hillsdale,NJ：Lawrence Erlbaum.Hou,L.K.,de la Torre,J.,&Nandakumar,R.(2014).Differential item functioning assessment in cognitive diagnosis modeling：Applying Wald test to investigate DIF for DINA model.

Journal of Educational Measurement,51

,98-125.Junker,B.W.,&Sijtsma,K.(2001).Cognitive assessment models with few assumptions,and connections with nonparametric item response theory.

Applied Psychological Measurement,25

,258-272.Kenward,M.G.&Molenberghs,G.(1998).Likelihood based frequentist inference when data are missing at random.

Statistical Science,13

,236-247.Leighton,J.,&Gierl,M.(2007).

Cognitive diagnostic assessment for education: Theory and applications

.Cambridge：Cambridge University Press.Li,F.M.(2008).

A modified higher-order DINA model for detecting differential item functioning and differential attribute functioning

(Unpublished doctorial dissertation).University of Georgia.Li,X.M.,&Wang,W.C.(2015).Assessment of differential item functioning under cognitive diagnosis models：The DINA model example.

Journal of Educational Measurement,52

,28-54.Louis,T.A.(1982).Finding the observed information matrix when using the EM algorithm.

Journal of the Royal Statistical Society,Series B,44

,226-233.Mantel,N.,&Haenszel,W.(1959).Statistical aspects of the analysis of data from retrospective studies of disease.

Journal of the National Cancer Institute,22

,719-748.Paek,I.,&Cai,L.(2013).A comparison of item parameter standard error estimation procedures for unidimensional and multidimensional item response theory modeling.

Educational and Psychological Measurement,74

,58-76.R Core Team (2015).

R: A language and environment for statistical computing.

R foundation for statistical computing,Vienna,Austria.Retrieved July 2,2015,from http：//www.R-project.orgRupp,A.A.,Templin,J.,&Henson,R.A.(2010).

Diagnostic measurement: Theory,methods,and applications

.New York,NY：Guilford.Shealy,R.,&Stout,W.(1993).A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF.

Psychometrika,58

,159-194.Sünbül,Ö.,&Sünbül,S.Ö.(2015,July).

Evaluating performance of differential item functioning detection methods for DIF data in DINA model

.Paper presented at the meeting of the annual meeting of the International Meeting of the Psychometric Society,Beijing,China.Swaminathan,H.,&Rogers,H.J.(1990).Detecting differential item functioning using logistic regression procedures.

Journal of Educational Measurement,27

(4),361-370.Templin,J.L.,&Henson,R.A.(2006).Measurement of psychological disorders using cognitive diagnosis models.

Psychological Methods,11

,287-305.Tian,W.,Cai,L.,Thissen,D.,&Xin,T.(2013).Numerical differentiation methods for computing error covariance matrices in item response theory modeling：An evaluation and a new proposal.

Educational and Psychological Measurement,73

,412-439.von Davier,M.(2005).

A general diagnostic model applied to language testing data (ETS Research Report RR-05-16).

Princeton：Educational Testing Service.von Davier,M.(2009).Some notes on the reinvention of latent structure models as diagnostic classification models.

Measurement:Interdisciplinary Research and Perspectives, 7

,67-74.Wang,Z.R.,Bian,Y.F.,&Guo,L.(2015).The impact of DIF on estimating accuracy of cognitive diagnostic test.

Psychological Exploration,35

,272-278.[王卓然,边玉芳,郭磊.(2015).项目功能差异对于认知诊断测验估计准确性的影响.

心理学探新,35

,272-278.]Wang,Z.R.,Guo,L.,&Bian,Y.F.(2014).Comparison of DIF detecting methods in cognitive diagnostic test.

Acta Psychologica Sinica,46

,1923-1932.[王卓然,郭磊,边玉芳.(2014).认知诊断测验中的项目功能差异检测方法比较.

心理学报,46

,1923-1932.]Zhang,W.(2006).

Detecting differential item functioning using the DINA model

(Unpublished doctorial dissertation).University of North Carolina at Greensboro.