Riemann Zeta函数ζ(s)的一种推导方法和证明

Riemann Zeta函数ζ(s)的一种推导方法和证明

黑宝骊，陈艳丽,及万会

(银川能源学院基础部,宁夏 银川 750105)

摘要：首先应用三角函数、双曲函数以及二者乘积的级数展开式，证明Riemann Zeta函数ζ(s)(s为偶数)时的一系列表达式，并得到一个表达形式较为简单的递推公式；同时应用此方法得到(p为正整数)时的一个递推公式，并应用留数基本定理逐一证明。

关键词：Riemann Zeta函数；双曲函数的级数；留数定理

中图分类号：O 156.1

作者简介：黑宝骊(1980-)，男，宁夏银川人，能源学院基础部教师。

DOI：10.3969/j.issn.1673-1492.2015.03.001

作者简介：王康佳(1986-)，男，河南焦作人，硕士研究生，主要研究方向为微波器件与电路。

A Derivation Method and Proof of Riemann Zeta Function

HEI Bao-li,CHEN Yan-li,JI Wan-hui

(Department of Basic Courses,Yinchuan Energy Institute,Yinchuan,Ningxia 750105,China)

Abstract:First,by using trigonometric function,hyperbolic function,and the two product series expansions, a series of expressions of the Riemann Zeta function ζ(s)(s is even)are proved.And a recursive formula with a relatively simpleexpression is obtained.(p is a positive integer)is obtained,and residue theorem is used to prove them one by one.

Key words:Riemann Zeta function；the series of hyperbolic function；residue theorem

在研究数论的一些问题时通常需要用到Riemann Zeta函数ζ(s)[1]，它的表达式为

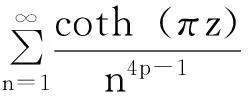
引理1[4]三角函数展开成级数如下(用数学软件Maple13展开求得)引理2[5](留数基本定理)如果函数f(z)在扩充复平面内只有有限个奇点，那么f(z)在所有各奇点(包括∞点)的留数总和必等于零。

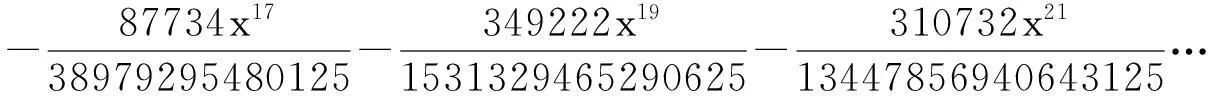
(1)

(2)

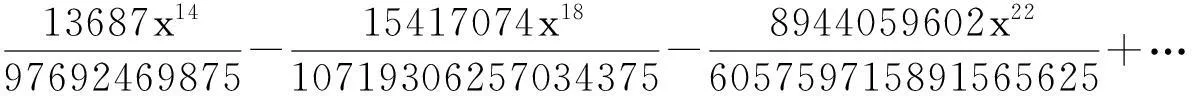
(3)

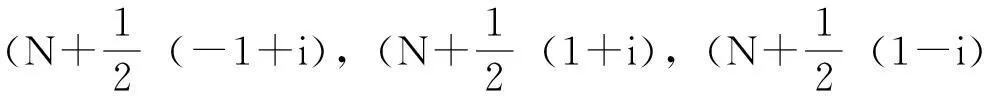
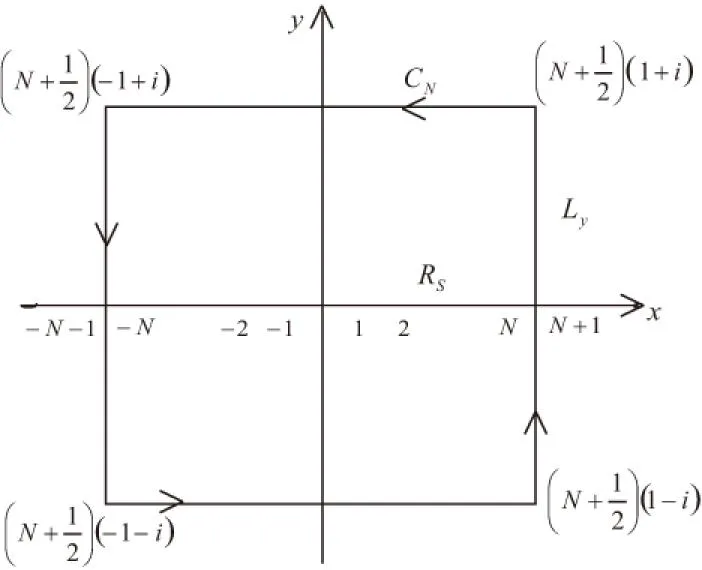
图1　函数f(z)在复平面内向四周扩充情况

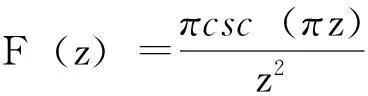
由引理1的级数(1)式，令x=πz，那么级数

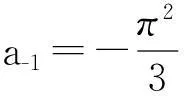
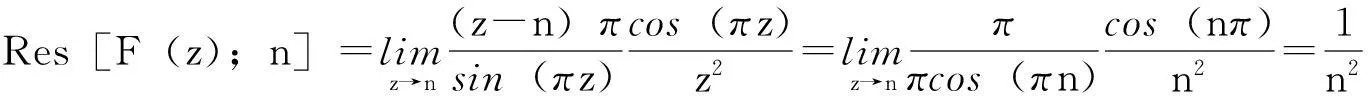
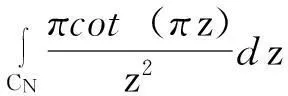
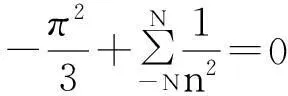
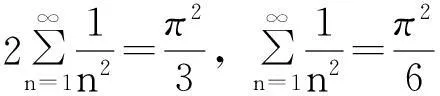
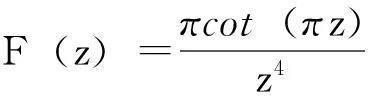
由引理1的级数(1)式，令x=πz，那么级数

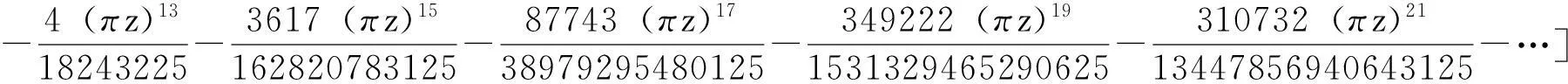
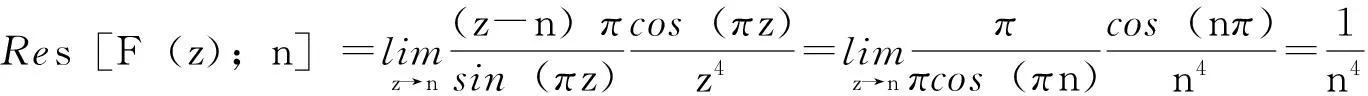
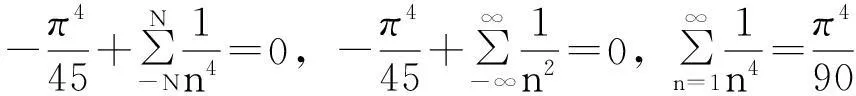
在z=n,n=±1,±2,…是单极点。由引理1的级数(1)式，令x=πz，那么级数

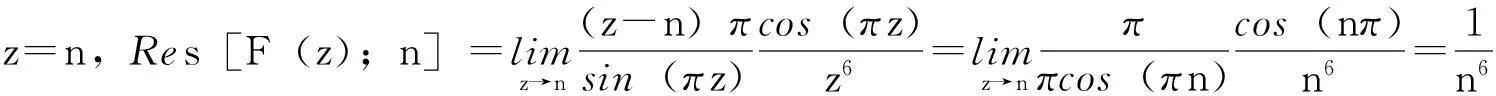
同法利用引理1的级数(1)式可得到

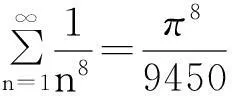
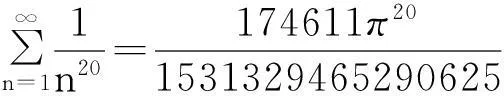
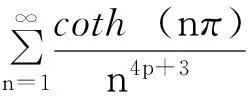
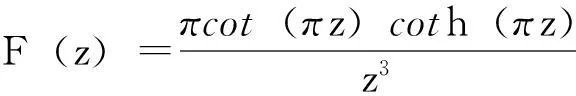
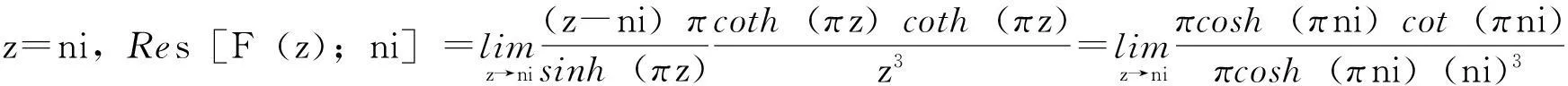
在单极点z=n,n=±1,±2,…

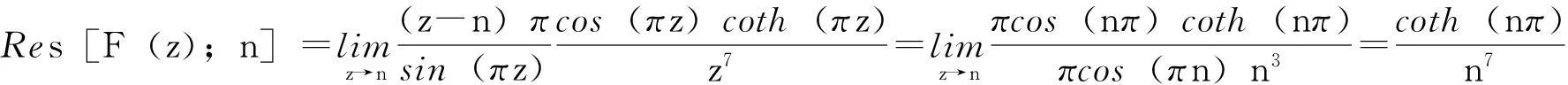
在单极点z=ni，n=±1,±2,…

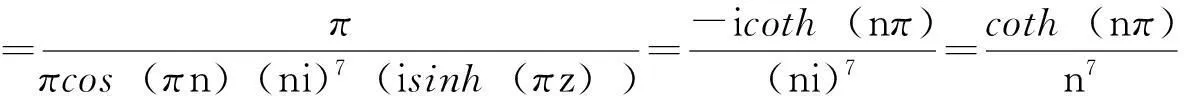
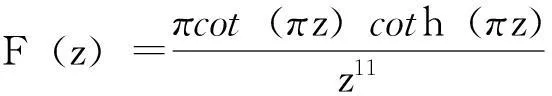
在单极点z=n,n=±1,±2,…

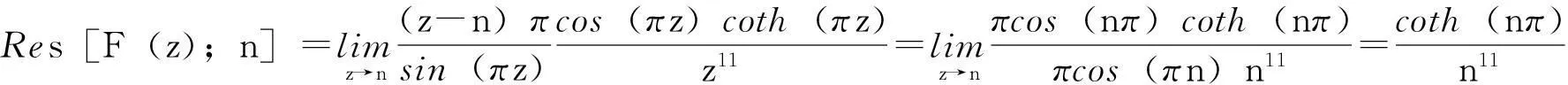
在单极点z=ni，n=±1,±2,…

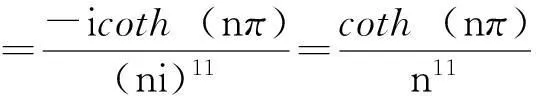
同法利用引理1的级数(3)式可得如下

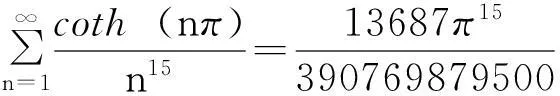
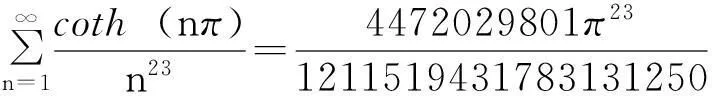
参考文献：

[1]Apostoil T M.Introduction to Analytic Number Theory[M].New York Inc:Spring-Verluy,1976:55.

[2]缪雪峰.Riemann Zeta函数ζ(2t)(t为正整数)的一个递推公式[J].福建教育学院学报，2005,5(07):122-123.

[3]及万会,吴永.双曲函数方幂和[J].纺织高校基础科学学报，2011，24(02)：246-249.

[4]Gradshteyn I S,Zyzhik I M.Table of Integral,Series and Products[M].Tenth ed.Academic Press,2007:42-48.

[5]盖云英，包革军.复变函数与积分变换[M].2版.北京：科学出版社,2007:127-128.

[责任编辑：郑秀亮英文编辑：刘彦哲]