磨合过程摩擦振动混沌吸引子演变规律
第一作者孙迪女,博士生,讲师,1979年12月生
通信作者李国宾男,博士,教授,1970年3月生
邮箱: guobinli88@163.com
磨合过程摩擦振动混沌吸引子演变规律
孙迪1,2,李国宾1,魏海军1,3,崔洋1,廖海峰2
(1.大连海事大学轮机工程学院,辽宁大连116026; 2.集美大学轮机工程学院,福建厦门361021;3.上海海事大学商船学院,上海200135)
摘要:在CFT-I型试验机上进行摩擦副磨合试验,应用混沌理论研究摩擦振动吸引子,探讨磨合过程中摩擦振动混沌吸引子的演变规律。结果表明,摩擦振动吸引子在相空间一定区域内具有特定层次结构且永不封闭轨迹。摩擦振动具有混沌行为的基本特征;随磨损过程的进行,摩擦振动混沌吸引子逐渐收缩并趋于稳定,混沌吸引子变化能反映摩擦副从磨合磨损到稳定磨损状态变化;摩擦振动混沌吸引子体积变化可用于摩擦副的磨合磨损状态预测与识别。
关键词:磨合;摩擦振动; 混沌;吸引子; 演变规律
收稿日期:2014-10-28修改稿收到日期:2014-12-05
中图分类号:TH117.2文献标志码:A
基金项目:国家自然科学基金资助项目(11372350,50875259);海军工程大学基金资助项目(HGDQNSQJJ3006)
Evolvement rule of frictional vibration chaos attractors in running-in process
SUNDi1,2,LIGuo-bin1,WEIHai-jun1,3,CUIYang1,LIAOHai-feng2(1.Marine engineering college, Dalian Maritime University, Dalian 116026,China;2.Marine engineering college, Jimei University,Xiamen 361021,China;3.Merchant marine college, Shanghai Maritime University,Shanghai 200135,China)
Abstract:Wear tests of a friction pair were conducted with a CFT-Ⅰtester. The frictional vibration signals were extracted and its attractors were studied by using the chaos theory. The variation law of frictional vibration chaos attractors in a wear process was explored. It was shown that the frictional vibration is characterized by chaos, and its chaos attractor has a specific hierarchy and a never closed trajectory in phase space; the chaos attractor of frictional vibration has a convergence trend at the beginning of running-in stage and tends to be in a stable state as a wear process goes on; the chaos attractor reveals the wear state variation from running-in wear to stable wear; therefore, the wear state of a friction pair can be predicted and identified by observing the volume change of chaos attractor of frictional vibration signals.
Key words:running-in; frictional vibration; chaos; attractors; evolvement rule
磨合作为机械系统使用的重要过程,其质量对延长机械系统工作寿命具有重要意义[1-2]。磨合为极复杂的非线性动力学过程,可用非线性理论研究磨合过程[3]。因此,分形[4-7]、混沌[8]等非线性理论在磨合研究中获得广泛应用。张怀亮等[9]计算磨粒轮廓分形维数,并用于磨粒自动识别及磨损状态检测。姬翠翠等[10]通过用分形理论研究磨损表面变化,证明此表面分形特征显著。朱华等[8,11]运用功率谱、分形维数及Lyapunov指数等3种方法联合证明摩擦信号混沌特征及磨合过程中吸引子的存在,认为磨合吸引子形成过程即摩擦学系统混沌行为轨迹由远离平衡态向平衡态收缩过程。
摩擦振动由摩擦副磨合中产生的自然现象,包含反映磨合状态信息。与摩擦系数、磨损表面及磨粒等信息相比,摩擦振动信号易于获取并可实时在线采集而不影响正常磨合过程。因此,用非线性理论进行摩擦振动研究可为磨合过程在线监测与识别提供新方法。然而,磨合过程摩擦振动吸引子是否具有非线性特征、如何重构吸引子及演变规律等尚待深入研究。因此,本文对磨合过程中摩擦振动混沌吸引子进行研究,探讨摩擦振动混沌吸引子产生原因及在磨合过程中的演变规律,为摩擦副磨合状态的分析提供参考。
1试验
试验在CFT-Ⅰ型摩擦磨损试验机上进行,原理见图1。用销-盘作为摩擦配副,销试样通过专用夹具固定,盘试样由专用夹具固定在台架上,电机经偏心轮机构将回转运动转换成往复运动带动台架及盘试样做往复滑动。载荷通过加载弹簧经销试样施加于盘试样。用PCB Piezotronics公司灵敏度100 mv/g、量程50 g 的356A16型ICP三轴加速度传感器测量振动信号,将其水平固定在盘试样下方。销、盘试样分别用线切割机从某船用柴油机的活塞环、缸套截取。盘试样保留珩磨的原始加工表面,接触表面为弧面,三维表面粗糙度为Sa=1.742 μm,尺寸Ø30 mm×10 mm,材质为合金铸铁,硬度HV300;销试样保留原始加工表面,接触表面为与缸套弧度相匹配的弧形表面,原始表面三维粗糙度Sa=0.674 μm,截面尺寸3 mm×4 mm,材质为合金铸铁,硬度HV600。电机转速600 r/min,销-盘试样相对运动的平均线速度0.1 m/s,润滑介质为普通的船用润滑油CD40,密度895.7 kg/m3,不间断滴油润滑。施加的正压力为30 N,名义接触载荷2.5 MPa。用INV-3062T2型信号采集仪采集振动信号,采样频率25.6 kHz,采样点4096。为获得不同试验阶段的表面形貌,本文在相同试验条件下设计5组不同时长的磨合磨损试验,时间分别为50 min,100 min,150 min,200 min,250 min,用OLYMPUS激光共聚焦显微镜(LSCM)对摩擦副表面形貌观察、测量。

图1 CFT-Ⅰ型摩擦磨损试验机原理图 Fig.1 Schematic diagram of CFT-Ⅰwear tester
2摩擦振动混沌吸引子分析方法
2.1吸引子的重构
本文据Takens定理[12]用C-C方法[13-14]重构摩擦振动吸引子。具体方法如下:
因此,m维矢量均为重构相空间的点X1,X2,…,XM可通过m维矢量重构摩擦振动吸引子。
可见嵌入维数m及延迟时间t 的选取对重构相空间至关重要。本文用C-C方法选取m及t,该方法延续了时间窗口概念,先定义关联积分,再构造统计量S(m,N,r,t)。
定义τs为时间序列采样间隔,τ为延迟时间,则时间序列延迟τd=ττs,延迟时间窗口τw=(m-1)τd,据统计量计算时间序列延迟τd,进而确定延迟时间t,再由时间窗口τw、τd确定嵌入维数m。计算时间序列的关联积分C(m,N,r,t)为
C(m,N,r,t)=

(1)
式中:θ(x)=0,(x<0);θ(x)=1(x≥0);关联积分表示相空间中任意两点间距小于r的概率。
{x1,xt+1,x2t+1,…}
{x2,xt+2,x2t+2,…}
…
{xt,x2t,x3t,…}
定义每个子序列统计量S(m,N,r,t)为
S(m,N,r,t)=
(2)
令N→∞有
(3)
若时间序列独立同分布,则对固定的m及t,当N→∞时对所有r,S(m,r,t)恒为零,但实际序列该值不为零。因此,局部最大时间间隔可取S(m,r,t)的零点或对所有半径r差别最小的时间点,此时这些点近似均匀分布。
定义差量为
ΔS(m,t)=
max{S(m,r,t)}-min{S(m,r,t)}
(4)
局部最大时间t对应S(m,r,t)零点或ΔS(m,t)最小值,时间序列延迟τd对应最大局部时间t中第一个,此时重构空间点最接近均匀分布,重构吸引子轨道在相空间完全展开,据第一个局部时间确定时间序列延迟τd,进而据τd=ττs求出延迟时间t。
嵌入窗选取要求S(m,r,t)与ΔS(m,t)均趋近于0,因此定义指标Scor(t)为
(5)

据式(3)~式(5)便可求出m及t。
2.2吸引子混沌判别方法
选吸引子轨迹法、功率谱法及Lyapunov指数法[15]判别摩擦振动信号的混沌特性。
2.2.1吸引子轨迹
吸引子是一般动力学系统随时间演变在相空间中形成的终极形态,是系统状态变化的方向及结局[15]。吸引子分不动点吸引子、极限环吸引子及奇异吸引子。不动点吸引子代表平衡态行为,在相空间中为一定点;极限环吸引子代表周期运动,在相空间中为一封闭曲线,见图2(a)周期仿真信号y= cos(80t)的吸引子;奇异吸引子亦称混沌吸引子,代表混沌运动,是相对稳定、收缩的,具分形结构的吸引子,在相空间中为一定区域内有一定分布形式或结构的永不封闭轨迹,见图2(b)混沌Chen信号吸引子。因此,可用吸引子状态判断时间序列是否具有混沌特征。
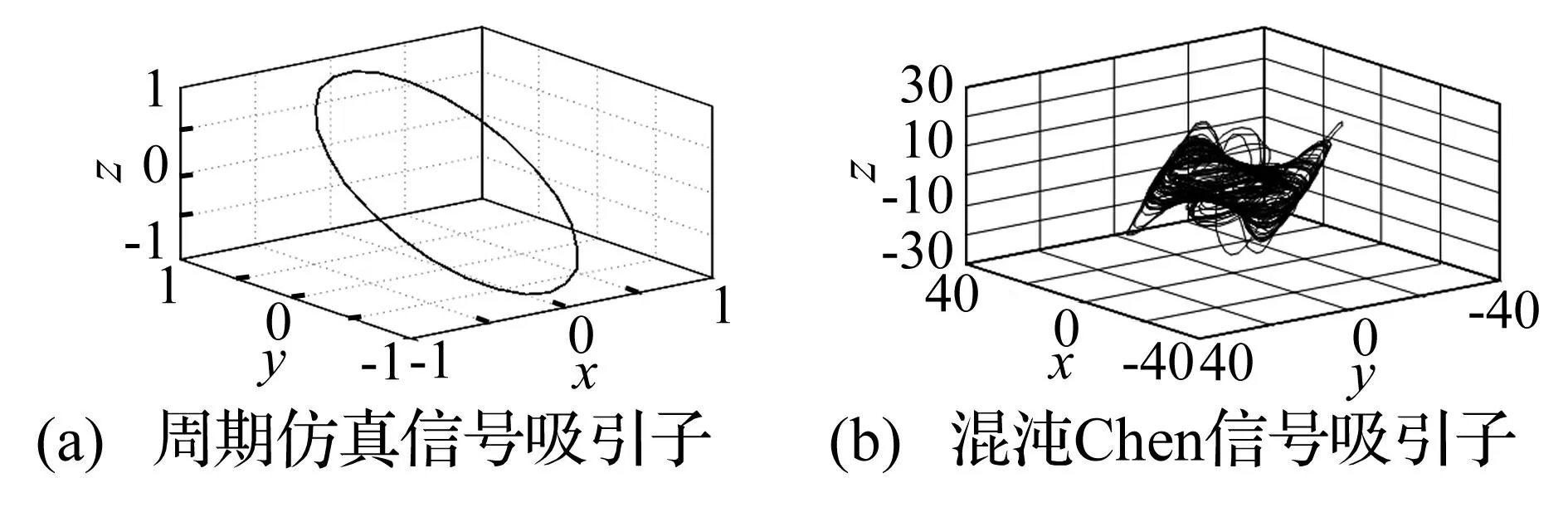
图2 仿真信号吸引子 Fig.2 Attractor of the simulation signals
2.3功率谱法
功率谱分析为研究振动、混沌的重要手段,对周期运动,功率谱在基频及倍频处出现尖峰,混沌运动在功率谱中为呈现噪声背景宽峰连续谱,无明显或成片峰值。图3(a)为含噪声的周期仿真信号y=cos(80t)+3cos(200t)的功率谱,可从无规则背景噪声中清晰分辨出40 Hz、100 Hz两个主峰。图3(b)为混沌的Chen信号功率谱,可见该功率谱在连续谱上叠加一定宽峰。因此,可据时间序列功率谱判断其混沌特性。

图3 仿真信号功率谱 Fig.3 Power spectrum of the simulation signals
2.4Lyapunov指数法
李雅普诺夫指数(Lyapunov Exponent)作为衡量系统动力学特性的重要指标,可表征系统在相空间中相邻轨道间收敛或发散的平均指数率[16]。格里波基证明只要最大Lyapunov指数(Maximum Lyapunov Exponent,MLE)大于零,即可肯定混沌存在。因此,据时间序列最大Lyapunov指数是否大于零可判断其是否具有混沌特征。
3结果与讨论
3.1摩擦振动吸引子混沌特征
试验采集的振动信号含噪声,未经降噪的振动信号不能真实反映摩擦副的磨合磨损过程,本文采用谐波小波包变换[17]法对采集的原始振动信号进行降噪处理,将信号分解成 7层64个频带,并重构第51~60频带。两组不同时刻原始、降噪后信号时域波形见图4。由图4看出,降噪后信号幅值明显减小,周期成分减弱。原始、降噪后信号吸引子见图5,由图5看出,原始信号吸引子运动轨迹无规律,而降噪后信号吸引子及Chen信号混沌吸引子特征相似,均在一定区域内有一定结构轨迹。降噪后摩擦振动信号功率谱及最大Lyapunov指数见图6、图7。由两图看出,降噪后摩擦振动信号功率谱无明显主峰,为出现噪声背景宽峰的连续谱,与Chen信号功率谱特征相似,且信号的MLE值为正值。因此,摩擦振动具有混沌特征,可通过混沌吸引子变化研究其特点。
3.2混沌吸引子演化
3.2.1变化规律
摩擦振动信号混沌吸引子的演化过程见图8。由图8看出,随试验进行,混沌吸引子呈现收缩趋势:前50 min收缩较快,50 min后其体积收缩明显减慢,150 min后体积趋于稳定,预示摩擦副磨合结束,进入稳定磨损状态。磨合过程中盘试样磨损表面粗糙度随磨合时间的变化曲线见图9。由图9看出,表面粗糙度变化经历由大到小过程,亦在150 min后趋于稳定,与摩擦振动混沌吸引子变化规律一致。因此,摩擦振动混沌吸引子的演化能反映摩擦副磨损状态变化。

图4 振动信号时域波形图 Fig.4 Waveform of original and noise-reduction vibration signals


图5 摩擦振动信号吸引子图Fig.5Attractoroffrictionvibrationsignal图6 摩擦振动信号功率谱Fig.6Powerspectrumoffrictionvibrationsignal图7 摩擦振动信号MLEFig.7MLEoffrictionvibrationsignal
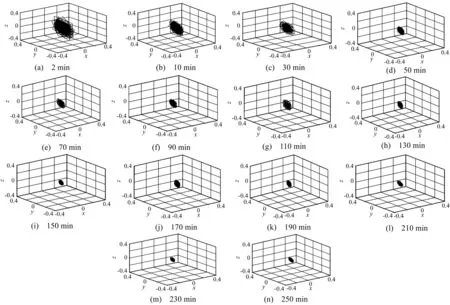
图8 摩擦振动信号混沌吸引子演化图 Fig.8 Chaos attractor evolution of frictional vibration signals

图9 磨损表面粗糙度随时间变化图 Fig.9 The variation of 3-D roughness of worn surface with time
3.2.2形成机理
3.2.2.1磨合阶段(0~150 min)
摩擦振动混沌吸引子变化与磨合过程中摩擦副磨损表面变化密切相关。磨合初期,摩擦副表面较粗糙,盘试样磨合前三维表面粗糙度为Sa=1.74 μm,表面磨损严重,摩擦振动强烈。摩擦振动不同时刻时域波形及频谱见图10。由图10(a)、(b)看出,磨合初期摩擦振动主峰明显、振幅较大,表明磨合过程产生能量较大,磨损过程处于不稳定状态,形成的摩擦振动吸引子体积较大(8(a))。由图10(c)、(d)看出,随磨合进行摩擦副表面逐渐光滑,第100 min时盘试样表面三维粗糙度从最初1.742 μm下降到1.204 μm,激发的摩擦振动减弱,振幅明显减小,且频率成分增多,主峰不明显。摩擦振动变化表明磨合过程损耗的能量减小,磨损趋于稳定,形成的摩擦振动吸引子体积逐渐收缩,向平衡态过渡。
3.2.2.2稳定磨损阶段(150~250 min)
当磨合过程进行到150 min后,摩擦振动混沌吸引子体积收缩并趋于稳定,形状更规则,表明摩擦副已达到磨合状态,进入稳定磨损阶段,摩擦副表面光滑,盘试样三维表面粗糙度均值为1.131 μm,表面磨损轻微,激发的摩擦振动减弱,见图10(e)、(f)。此时磨合过程损耗能量减小,磨损进入平稳状态,摩擦振动混沌吸引子呈体积小、稳定、形状规则等特征。
摩擦振动混沌吸引子在磨合过程中的变化表明,磨损过程即能量耗散过程,摩擦学系统为非线性耗散的动力系统。对磨合系统而言,随磨损过程进行,磨损表面愈光滑摩擦激发的能量愈小,摩擦振动强度逐渐减小,其混沌吸引子亦呈收缩趋势。

图10 摩擦振动信号时频图 Fig.10 Waveform and spectrum of frictional vibration signal
4结论
摩擦振动含反映摩擦副磨合磨损状态信息,本文用混沌理论研究摩擦副磨合磨损过程中振动信号,探讨摩擦振动混沌吸引子演变,结论如下:
(1)摩擦振动吸引子为相空间中有限区域内具有一定层次结构的轨迹,摩擦振动信号功率谱为宽峰连续谱,最大Lyapunov指数均为正值;摩擦振动具有混沌特征。
(2)摩擦振动混沌吸引子在磨合磨损过程中逐渐收缩并趋于稳定;摩擦振动吸引子能反映摩擦副从磨合磨损到稳定磨损的状态变化。因此,摩擦振动吸引子可用于摩擦副磨合磨损状态识别。
参考文献
[1]葛世荣,朱华. 摩擦学复杂系统及其问题的量化研究方法[J]. 摩擦学学报,2002,22(5):405-408.
GE Shi-rong, ZHU Hua.Complicate tribological systems and quantitative study methods of their problems[J]. Tribology,2002,22(5):405-408.
[2]周俊杰,赵军.磨合过程摩擦表面分形参数研究[J]. 汽车工程学报,2011,5(1):469-473.
ZHOU Jun-jie,ZHAO Jun. The fractal parameters of surface profile during running-in process[J].Chinese Journal of Automotive Engineering, 2011,5(1):469-473.
[3]朱华,陆斌斌,历建全,等.摩擦学问题研究的非线性理论方法[J]. 机械工程学报,2010.46(15):82-88.
ZHU Hua, LU Bin-bin, LI Jian-quan,et al. Nonlinear theory and methods of researching tribological problems [J].Journal of Mechanical Engineering,2010,46(15):82-88.
[4]Ge S R, Chen G A, Zhang X Y. Fractal characterization of wear particle accumulation in the wear process[J]. Wear, 2001,251:1227-1233.
[5]Ji C C, Zhu H, Jiang W,et al. Running-in test and fractal methodology for worn surface topography characterization [J]. Chinese Journal of Mechanical Engineering, 2010, 23(5): 600-605.
[6]Zhu H, Ge S R, Cao X C,et al. The changes of fractal dimensions of frictional signals in the running-in wear process[J]. Wear, 2007,263:1502-1507.
[7]朱华,葛世荣.摩擦力和摩擦振动的分形行为研究[J]. 摩擦学学报,2004,24(5):433-437.
ZHU Hua, GE Shi-rong. Study on the fractal behaviors of frictional forces and vibrations[J]. Tribology, 2004, 24(5): 433-437.
[8]朱华,葛世荣.摩擦学系统的混沌特性[J].机械工程学报, 2004,40(12):10-13.
ZHU Hua, GE Shi-rong. Chaotic characteristics of tribological systems[J]. Chinese Journal of Mechanical Engineering, 2004, 40(12):10-13.
[9]张怀亮,孙栓辉. 片状磨粒、块状磨粒和层状磨粒轮廓分形维数研究[J].润滑与密封,2009,134(112):37-40.
ZHANG Huai-liang, SUN Shuan-hui. The Fractal dimension of profile of chip, blocky and laminar wear particles[J]. Lubrication Engineering, 2009,134(112): 37-40.
[10]Ji C C,Zhu H, Jiang W,et al. Running-in test and fractal methodology for worn surface topography characterization[J]. Chinese Journal of Mechanical Engineering,2010,23(5):600-605.
[11]朱华,葛世荣,吕亮,等. 磨合吸引子的演变规律[J]. 机械工程学报, 2008, 44(3): 99-103.
ZHU Hua, GE Shi-rong, LÜ Liang,et al. Evolvement rule of running-in attractor [J]. Chinese Journal of Mechanical Engineering, 2008, 44(3): 99-103.
[12]Takens F. Detecting strange attractors in turbulence [J]. Lecture Notes in Mathematics, 1981,898:366-381.
[13]陆振波,蔡志明,姜可宇. 基于改进的 C-C 方法的相空间重构参数选择[J].系统仿真学报.2007.19(11):2527-2529.
LU Zhen-bo, CAI Zhi-ming, JIANG Ke-yu. Determination of embedding parameters for phase space reconstruction based on improved C-C method[J]. Journal of System Simulation(S1004-731X), 2007, 19(11): 2527-2529.
[14]胡瑜,陈涛.基于 C-C 算法的混沌吸引子的相空间重构技术[J].电子测量与仪器学报,2012,26(5): 425-430.
HU Yu, CHEN Tao. Phase-space reconstruction technology of chaotic attractor based on C-C method[J]. Journal of electronic Measurement and Instrument,2012, 26(5): 425-430.
[15]姜万录,张淑清,王益群.基于混沌和小波的故障信息诊断[M].北京:国防工业出版社,2005.
[16]马晋,江志农,高金吉. 基于混沌分形理论的特征提取技术在气阀故障诊断中应用[J]. 振动与冲击,2012, 31(19): 26-30.
MA Ji, JIANG Zhi-nong, GAO Jin-ji. Feature extraction method based on chaotic fractal theory and its application in fault diagnosis of gas valves[J]. Journal of Vibration and Shock,2012,31(19): 26-30.
[17]李国宾,关德林,李廷举. 基于小波包变换和奇异值分解的柴油机振动信号特征提取研究[J].振动与冲击,2011,30(8):149-152.
LI Guo-bin,GUAN De-lin,LI Ting-ju.Feature extraction of diesel engine vibration signal based on wavelet packet transform and singularity value decomposition [J]. Journal of Vibration and Shock,2011,30(8):149-152.


