考虑气动阻尼效应的输电线路风偏动态分析方法
第一作者楼文娟女,教授,博士生导师,1963年生
邮箱:louwj@zju.edu.cn
考虑气动阻尼效应的输电线路风偏动态分析方法
楼文娟1,杨悦1,吕中宾2,张少锋2,杨伦1
(1.浙江大学结构工程研究所,杭州310058;2.河南电力试验研究院,郑州450052)
摘要:针对连续多跨输电线路在瞬态风场作用下的风偏问题,提出考虑气动阻尼效应的输电线路风偏动态分析方法。以500 kV三跨线路为对象建立精细化非线性动力学计算模型,用谐波叠加法构建整档线路各点脉动风速场并结合准定常假设模拟作用于输电线路的时变风荷载。考察由输电线路自身运动引起的气动阻尼对动态风偏响应影响,讨论其对绝缘子串风偏角频谱影响。采用美国输电线路设计规范ASCE No.74的气动阻尼进行导线风偏计算,并与所提方法比较。结果表明,输电线路气动阻尼对风偏动态响应影响显著,两种考虑气动阻尼方法计算结果较接近。
关键词:风偏;气动阻尼;多跨线路;瞬态风场;非线性动力分析
收稿日期:2013-12-19修改稿收到日期:2014-04-01
中图分类号:TM75文献标志码:A
基金项目:国家自然科学
Windage yaw dynamic analysis methods for transmission lines considering aerodynamic damping effect
LOUWen-juan1,YANGYue1,LÜZhong-bin2,ZHANGShao-feng2,YANGLun1(1. Research Institute of Structure Engineering, Zhejiang University, Hangzhou 310058, China; 2. Henan Electric Power Testing and Research Institute, Zhengzhou 450052, China)
Abstract:Electrical power transmission systems are severely threatened by flashover accidents caused by windage yaw. Here, a nonlinear dynamic transmission line model consisting of three-span electrical conductors was established precisely by using the finite element method. Then, the fluctuating wind speed field around the transmission line was built with the harmonic wave superposition method and the time-varying wind loads acting on the line were simulated with the quasi-steady assumption. The time and space correlation characteristics between different simulated points were taken into account. Furthermore, the impact of aerodynamic damping caused by conductor movements on the windage yaw dynamic response of the transmission line was investigated. The aerodynamic damping gained with the US transmission line design code ASCE No.74 was adopted to compute the windage yaw dynamic response of the line. The results of the two methods were compared. It was shown that the aerodynamic damping can reduce the maximum value of the windage yaw dynamic response of the line significantly, but have no remarkable effect on its average value; the results of the two methods are close to each other.
Key words:windage yaw; aerodynamic damping; multi-span; fluctuating wind field; nonlinear dynamic analysis
风偏指输电线路在风荷载作用下的面外摆动。导线或绝缘子串金具与输电杆塔过近时会产生放电闪络,而线路风偏闪络后跳闸的重合成功率较低,严重威胁电网系统正常运行,并引发大规模停电事故,会造成巨大经济损失及社会影响[1]。基于此,本文提出输电线路风偏合理计算方法,对保障电网系统的安全运行有重要意义。
国外对输电线路风偏的研究起步较早,其中日本及部分北美国家针对输电线路风偏问题率先展开实测研究与理论分析[2-4]。Tsujimoto等[5]基于真型输电线路的风偏观测及理论分析,给出用于计算单跨导线相间安全距离的静力计算模型。Rikh[6]以保证悬垂串导线与杆塔间最小安全间隙为设计准则,利用图解法计算导线风偏角。以往研究[7-8]包括现行国内规范均采用静力模型进行风偏计算。朱宽军等[9-10]提出应考虑脉动风速对输电线路的动力效应,并进行风偏动态响应分析,但未考虑气动阻尼影响,从而高估了风偏的动态响应。Homles[11]曾通过数学方法给出与塔顶位移有关的格构式输电塔气动阻尼计算公式,认为在研究风致输电塔气动效应时,气动阻尼作用显著。导线的风偏位移较格构式输电塔大,因此气动阻尼效应更明显,对风偏影响不可忽略。本文在输电线路非线性动力方程中引入结构与来流间相对运动,建立考虑气动阻尼的风偏计算方法。通过500 kV三跨输电线路计算分析,考察输电线路自身运动引起的气动阻尼对动态风偏响应影响,并与用文献[12](给出的气动阻尼公式所得)风偏值进行对比。
1输电线路考虑气动阻尼的动力方程
研究表明[13],发生风致振动时,结构与来流间相对运动效应会使动力系统阻尼增大,而新增阻尼即为附加于结构的气动阻尼,其具有随平均风速增大而增大特征。输电线路跨度长、阻尼小、柔度大,属于典型的对风荷载敏感非线性结构,风偏位移大,故求解导线风偏响应时应考虑气动阻尼影响。
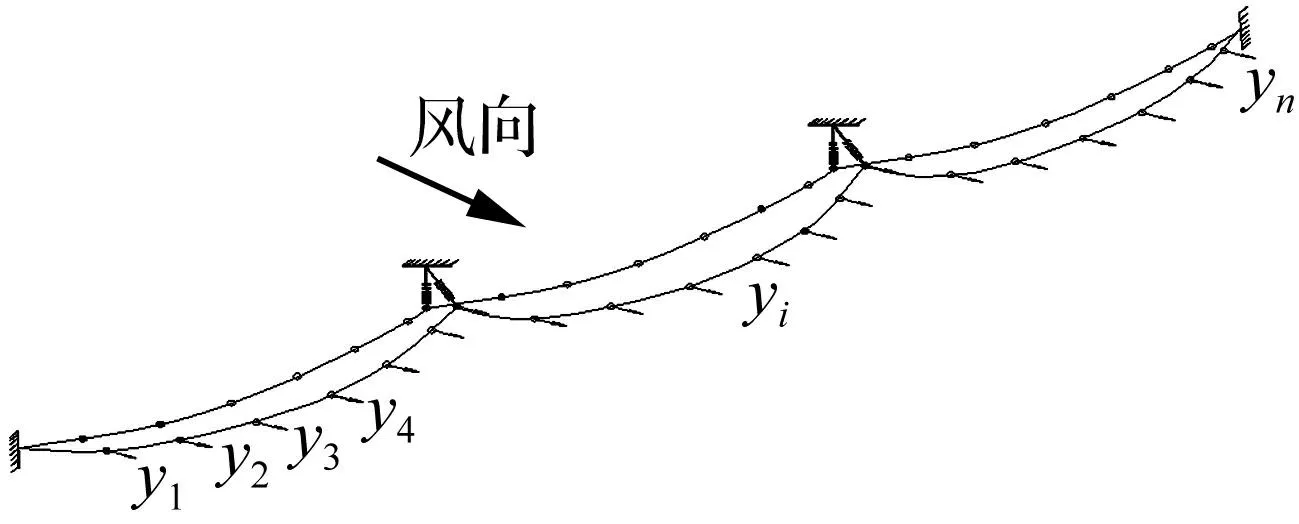
图1 多自由度导线俯视图 Fig.1 Multi-degree model of transmissionline
为详细说明导线气动阻尼产生机理及作用特征,引入n自由度多跨输电线路,见图1。在风荷载作用下顺风向位移向量Y可表示为
Y=[Y1,Y2,…,Yn]T
(1)
式中:Yi为第i点顺风向位移。
输电线路非线性运动方程可写为
(2)
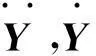
KT(Y)=KL+KN(Y)+Kσ(Y)
(3)
式中:KL,KN(Y),Kσ(Y)分别为线性、非线性刚度矩阵及应力刚化矩阵;F为作用于输电线路结构的风荷载时程矩阵,不考虑结构与来流相对运动时,F可表示为
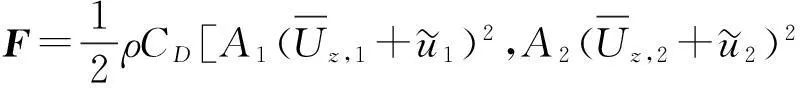
(4)
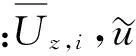
由式(4)不难发现,不考虑气动阻尼时,作用于导线的风荷载仅与风速及截面气动参数有关。考虑导线与来流的相对运动效应时,式(2)右端风荷载为
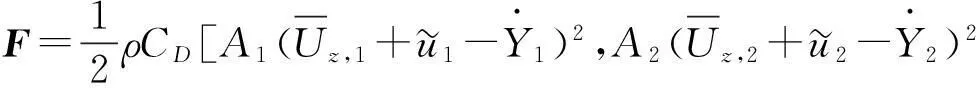
(5)
(6)
式(6)右边F1,F2分别为
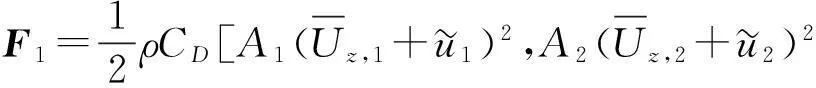
(7)
(8)
由于F2是导线运动速度的平方项为小量可忽略,左边Caero即为由导线自身运动所致气动阻尼矩阵,即
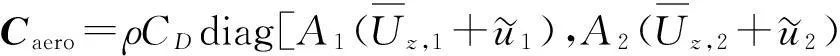
(9)
2ASCE No.74提供的气动阻尼
ASCE No.74给出的导线气动阻尼计算方法为
ξa=0.000 048(V0/fw(d/12))Cf
(10)
式中:V0为导线有效高度处10 min平均风速;d为导线直径;Cf为导线体型系数;fw为平面外摆动的基础频率,计算式为
fw=(1/sag)0.5
(11)
式中:sag为中跨弧垂长度。
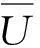
C=αM+βK
(12)
式中:α,β为由结构总阻尼比ξ、前两阶基本频率ω1,ω2决定的常系数,即
(13)
(14)
求解非线性运动方程(6)时,输电线自身结构阻尼ξs取0.005;采用气动阻尼[12]计算导线风偏时,在阻尼矩阵中直接考虑气动阻尼影响,ξ=ξs+ξa。
3多点脉动风速模拟
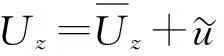
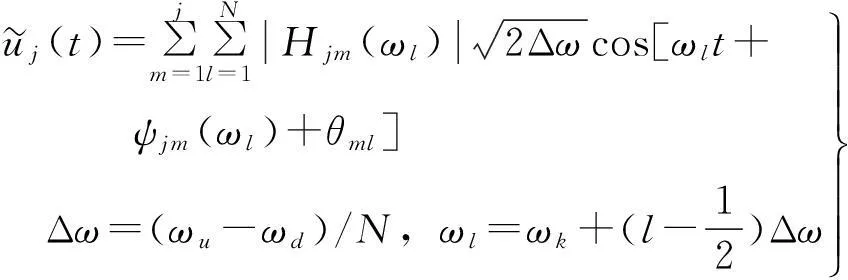
式中:ωu,ωd分别为模拟风速时圆频率上、下限;N为频率划分段数;Δω为圆频率增量,θjm为均匀分布于[0,2π]的随即相位角;ψjm(ωl)为i,j两点间相位角;Hjm(ωl)为下三角矩阵H(ωl)中元素,H(ωl)可通过对互谱矩阵S(ωl)进行Cholesky分解求得,即
S(ωl)=H(ωl)H*(ωl)T
(16)
式中:S(ωl)为互功率谱矩阵,即
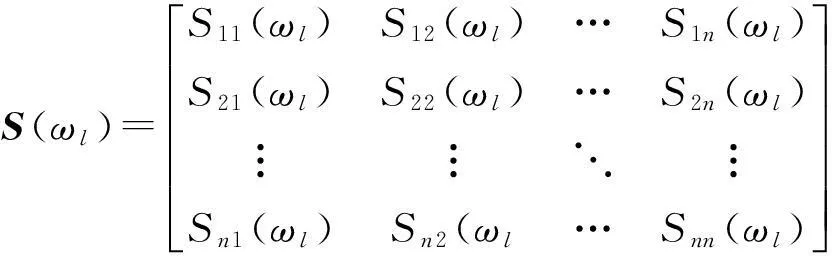
(17)
式中:Sij(ωl)为i,j两点间互谱密度函数,即
(18)
式中:Cohij(ω)为i,j两点的空间相关函数,可用Davenport推荐公式求得,即
Cohij(ω)=
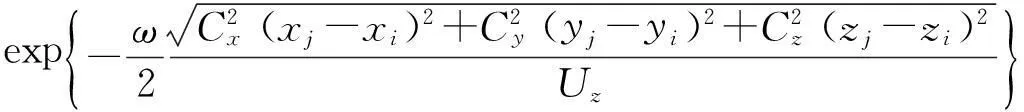
式中:Cx=16,Cy=6,Cz=10分别为x,y,z方向的衰减系数。
式(17)中Sij(ω)为脉动风速风功率谱密度函数,本文选Davenport谱,即
(20)
式中:x=1200ω/U10;ω为圆频率;k为系数,与地貌有关。
需要指出的是,Davenport谱具有典型的区域代表性,但其代表的能量在不同高度处完全相同,因此不能反映脉动风速湍流度沿高度变化规律。虽相关资料[15]已给出式(16)中地貌系数k的建议值,但脉动风速模拟值均方根等统计特征并不一定能与规范的理论湍流剖面吻合。因此,需据结构所在地域大气湍流沿高度变化特征,对Davenport谱进行修正。湍流度Iz与风谱存在关系为
Iz=σu/Uz
(21)
(22)
考虑沿高度变化的湍流度及风速剖面,定义风谱修正系数Qz为
(23)
式中:Iz,T为规范中湍流剖面理论值。
(24)
4动态风偏算例
4.1计算模型
以某500 kV连续三跨输电线路为例,其中线路两端杆塔为耐张杆塔,其余杆塔为直线塔。各跨导线几何参数见图2。输电线路所用导线形式为四分裂导线,子导线型号为LGJ-400/35,物理参数见表1。绝缘子串长5 m,单根重量34 kg。
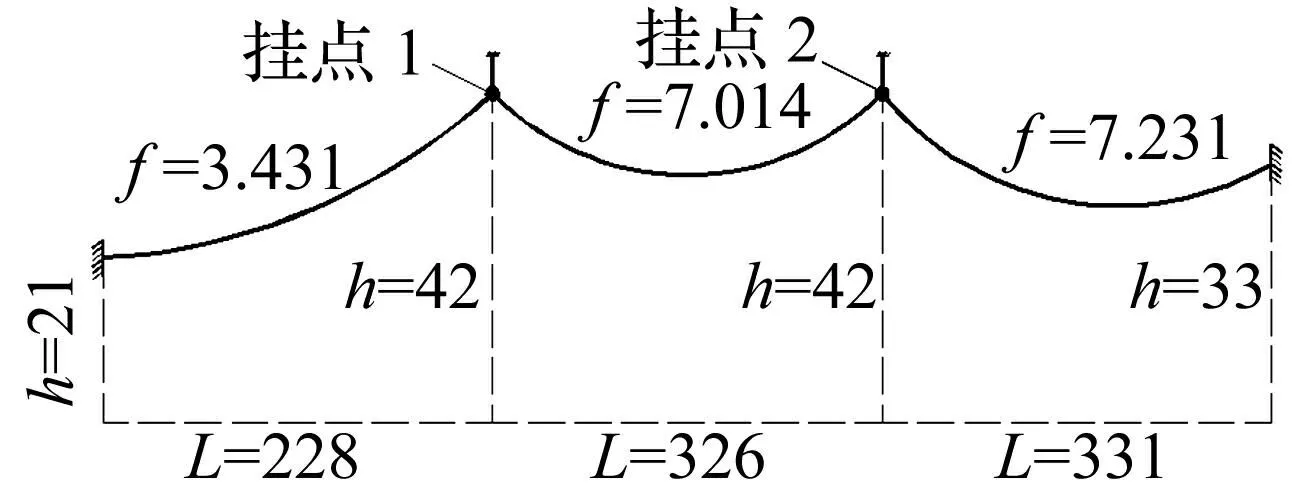
图2 500 kV线路示意图 Fig.2 The figure of 500 kV transmission line

计算截面积/mm2外径/mm弹性模量/MPa线密度/(kg·km-1)运行张力/kN425.2426.8265000134925.06
鉴于导线风偏主要以顺风向位移为主,输电塔风致振动响应对导线路风偏影响不大,考虑计算分析效率,在建立有限元模型时不考虑杆塔影响。将绝缘子串与杆塔连接设为固定铰接。四分裂导线发生风偏时主要以整体摆动为主,故在模型中可按等效原则将分裂导线视为一根。输电导线属于非线性特征显著的高柔度结构,因此仅能受拉而不能受压且无法承受弯矩,故本文采用ANSYS有限元软件的Link10单元模拟;而对风偏发生时始终受拉的绝缘子串采用Link8单元模拟;在导线非线性计算中打开ANSYS中大位移、大变形开关。绝缘子串重量以附加质量形式融合到有限元模型中,采用Mass 21单元模拟。此外,综合考虑非线性动力分析的收敛性及计算效率等因素影响,导线单元长度约取10 m,共划分90个单元。
4.2时域计算结果与讨论
考虑到导线风偏主要以面外摆动为主,多跨线路自振基频均较低,因此模拟风速时截止圆频率ωu=2π;为保证脉动风速时程中低频部分不被过滤掉,频率划分段数N=2 048,圆频率增量Δω=3.068 0×10-3rad/s;据采样定理,风速模拟总时距T=2π/Δω=2 048 s;为防止风速模拟过程中发生混叠、失真,时域划分段数Nt应满足Nt>2N,结合导线有限元时域分析的收敛性条件,风速模拟时取Nt=32N=65 536,荷载时间步长Δt=0.031 25。
输电线路绝缘子串(图2中挂点1)处考虑脉动后的风速时程见图4。值得一提的是,为消除突加荷载冲击放大效应影响,在风速时程前100 s加入风速由0增至风速平均值的线性增长过程。挂点1处脉动风速功率谱目标值及模拟值对比见图5。由图5看出,风功率谱目标值与模拟值吻合较好,说明所得风速时程能有效反应脉动能量在频率内的分布特征。篇幅所限,其余各点处风速时程及功率谱不再给出。
按式(21)所得风场湍流度模拟值与湍流剖面理论值对比见图6。由图6看出,风场湍流度的模拟值与理论值吻合较好,说明采用修正后的Davenport谱模拟所得风速能有效反映风场湍流度沿高度的变化规律。


图4 1号挂点处风速时程Fig.4Timehistoryofwindvelocityatsuspensionpoint1图5 1号挂点脉动风速功率谱Fig.5Powerspectrumfunctionofwindvelocityatsuspensionpoint1图6 风场湍流度模拟值与理论值对比Fig.6Thecomparisonofturbulencebetweennumericalandtheoreticalmethod
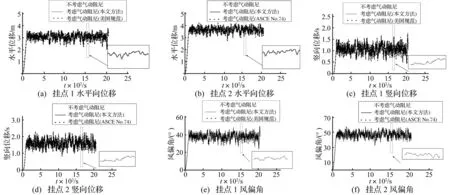
图7 挂点1、2处的风偏响应时程 Fig.7 The dynamic responses of windage yaw at suspension point1and suspension point 2
将谐波叠加法模拟所得脉动风荷载时程加载至有限元模型的91个节点,采用无条件稳定的Newmark法对非线性动力方程直接积分求解,并运用Newton-Raphson法对每个时间步末尾位移进行迭代。
考虑、不考虑气动阻尼影响三种情况下挂点水平向、竖直向位移时程及风偏角时程见图7。由图7看出,在气动阻尼作用下,输电线路风偏响应振动幅值明显降低,表明由系统自身运动状态引发的气动阻尼为正,对降低输电线路的动态风偏响应有利;在挂点处整个时程中,两种考虑气动阻尼方法对导线风偏影响十分接近,说明ASCE No.74中的气动阻尼简化计算方法可用于导线风偏计算。
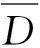
(26)
为使式(26)中风偏角极值具有98.61%的保证率,保证因子g取2.2[14]。三种情形下三跨线路各节点位移平均值与极大值对比见图8。由图8看出,气动阻尼能显著降低风偏响应极大值,但对平均值几乎无影响;相比导线跨中位置,挂点处单摆半径小,气动阻尼降低风偏响应效果不明显;两种气动阻尼(本文方法与ASCE No.74)对风偏响应影响较接近,考虑ASCE No.74给出的气动阻尼值时,输电线路位移稍大,偏于安全;对比输电线路不同位置处位移进一步发现,受线路耐张塔边界条件约束效应及各档距导线弧垂影响,离支座越近的节点风偏响应越小,各档距中点位置位移较挂点处位移大得多。
图8 各点风偏统计值 Fig.8 The statistical values of windage yaw at every point
现实中导线风偏闪络多由绝缘子挂点处与横担距离过近导致。图2中挂点2的风偏角动态求解结果对比见表2。由表2看出,①考虑导线气动阻尼后,风偏角得以降低。由于绝缘子串挂点处单摆半径较小,折减效应并无导线跨中明显;②本文考虑相对运动速度产生的气动阻尼与ASCE No.74的导线气动阻尼计算式(22)对导线作用较接近,说明ASCE No.74中气动阻尼计算方法可在风偏研究时采用。
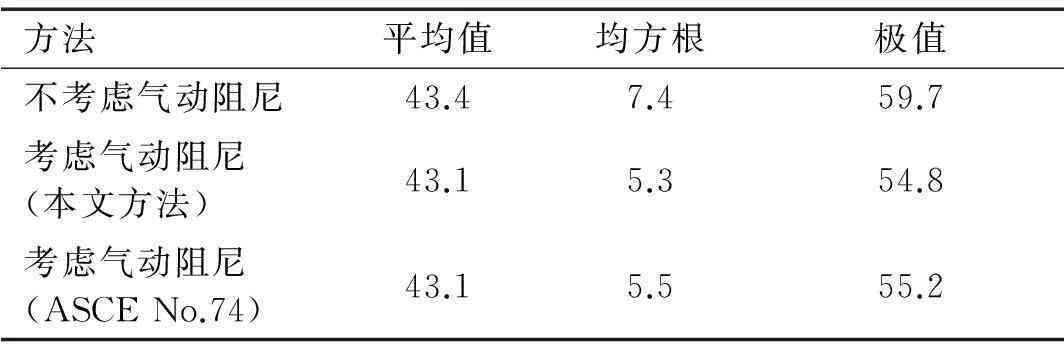
表2 挂点2风偏角平均值、均方根、极值计算结果(°)
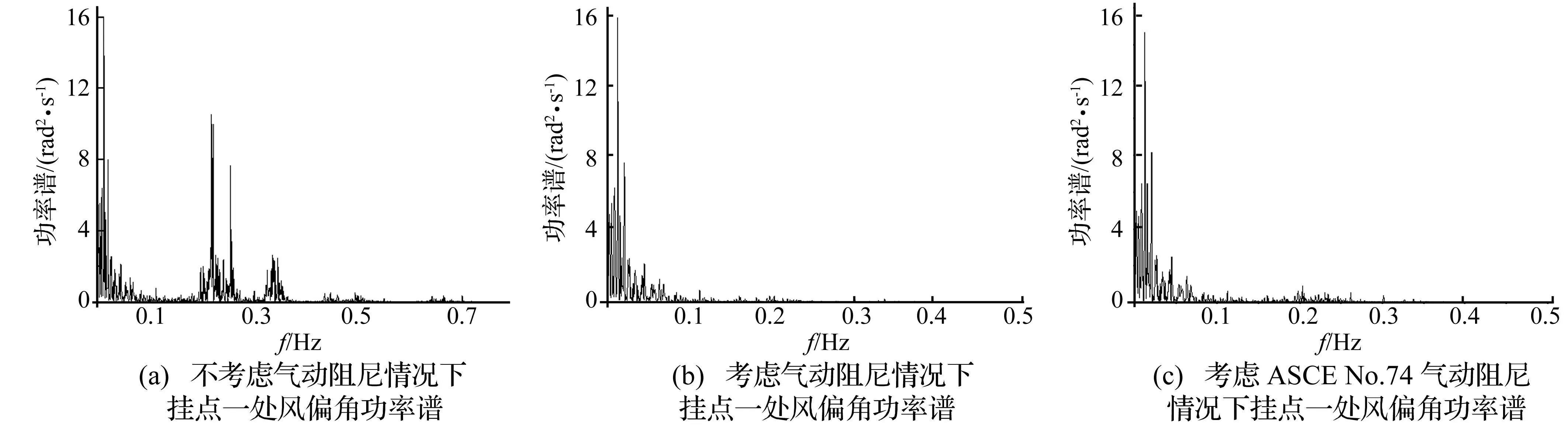
图9 挂点1处风偏角功率谱 Fig.9 The power spectrum of windage angle at suspension point 1
4.3频域计算结果与讨论
结构振动响应含两部分,即背景分量、共振分量。前者仅与风荷载脉动特征有关,后者主要与结构自身动力特性有关。从功率谱角度,背景分量主要集中在风致振动响应的低频部分,而共振分量部分能量主要集中在结构低阶自振频率附近,具有十分显著的峰值。为比较在输电线路风偏计算中是否考虑气动阻尼对共振分量及背景分量影响,将挂点1处绝缘子串风偏角时程进行傅里叶变换为频率谱。分别考虑、不考虑气动阻尼时绝缘子串风偏响应功率谱见图9。由图9看出,不考虑气动阻尼时,风偏响应共振效应十分明显,且主峰值对应输电线路一阶自振频率;考虑气动阻尼后共振分量大幅降低,采用ASCE No.74的气动阻尼值与本文计算气动阻尼方法所得风偏角功率谱十分相似。由于导线气动阻尼普遍存于实际中,因此在计算风偏响应时可忽略共振分量对风致振动影响。
5结论
本文以500 kV四塔三档输电线路为研究对象,建立考虑气动阻尼的导线风偏非线性动力控制方程,采用非线性瞬态分析方法求解输电线路的动态风偏响应,结论如下:
(1)输电线路的风偏虽以静态值(时均值)为主,但脉动值不可忽略,尤其在导线跨中部位,动态风偏较大;
(2)导线与气流的相对运动会产生显著的气动阻尼,在高风速下该阻尼大于导线本身的结构阻尼,能显著降低导线风偏响应的脉动值;
(3) ASCE No.74中的气动阻尼简化计算方法可应用于导线风偏动态计算。
(4)因存在气动阻尼,实际风偏计算中可忽略导线与来流风间的共振作用。
参考文献
[1]闵绚, 邵瑰玮, 文志科,等. 国内外悬垂绝缘子串风偏设计参数对比与分析[J].电力建设,2013, 34(4): 19-26.
MIN Xuan, SHAO Gui-wei, WEN Zhi-ke, et al. Analysis onwindage design parameters of suspension[J]. Electric Power Construction, 2013, 34(4):19-26.
[2]Hiratsuka S, Matsuzaki Y, Fukuda N, et al. Field test results of a low wind-pressure conductor[J]. Proceedings of IEEE Region 10 International Conference on,IEEE, 2001, 2: 664-668.
[3]St Clair J G. Clearance calculations of conductors to buildings[C].Transmission and Distribution Conference, IEEE, 1996: 493-498.
[4]Allen L. Calculation of horizontal displacement of conductors under wind loading toward buildings and other supporting structures[C]. Papers Presented at the 37th Annual Conference, IEEE, 1993: A1/1-A1/10.
[5]Tsujimoto K, Yoshioka O, Okumura T, et al. Investigation of conductor swinging by wind and its application for design of compact transmission line[J]. Power Apparatus and Systems, IEEE Transactions on, 1982 (11): 4361-4369.
[6]Rikh V N. Conductor spacings in transmission lines and effect of long spans with steep slopes in hilly terrain[J]. IE (I) Journal, 2004, 85(5): 8-16.
[7]龙立宏, 胡毅, 李景禄,等. 输电线路风偏放电的影响因素研究[J]. 高电压技术, 2006, 32(4): 19-21.
LONG Li-hong,HU Yi,LI Jing-lu,et al. Study on windage yaw discharge of transmission line[J]. High Voltage Engineering, 2006,32(4):19-21.
[8]王声学, 吴广宁, 范建斌, 等. 500 kV 输电线路悬垂绝缘子串风偏闪络的研究 [J]. 电网技术, 2008, 32(9): 65-69.
WANG Sheng-xue,WU Guang-ning,FAN Jian-bin,et al. Study on Flashover of suspension insulator string caused by windage yaw in 500 kV transmission lines [J]. Power System Technology, 2008,32(9):65-69.
[9]朱宽军,邸玉贤,李新民,等. 安装相间间隔棒的输电线防风偏设计有限元分析[J]. 高电压技术, 2010,36(4):1038-1043.
ZHU Kuan-jun, DI Yu-xian, LI Xin-min,et al. Analysis ofoverhead transmission line for asynchronous swaying by the finite element method[J]. High Voltage Engineering, 2010, 36(4):1038-1043.
[10]Yan B, Lin X, Luo W, et al. Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load[J]. Power Delivery, IEEE Transactions on, 2010, 25(1): 248-259.
[11]Holmes J D. Along-wind response of lattice towers-Ⅱ, aerodynamic damping and deflections[J]. Engineering Structures, 1996,18(7):483-488.
[12]ASCE: Guidelines for electrical transmission line structural loading. published by the american society of civil engineers No.74, 2003[S].
[13]Souza L.The behavior of transmission lines under high wind[D]. Ontario: The university of western Ontario,1996.
[14]张相庭. 结构风工程理论.规范.实践[ M] . 北京: 中国建筑工业出版社, 2006.


