基于固定鸭舵的弹道修正弹建模与仿真

基于固定鸭舵的弹道修正弹建模与仿真

张开创1,刘秋生1,王龙2

(1军械工程学院 弹药工程系,石家庄 050003;2总装备部驻葫芦岛地区代表室,辽宁 葫芦岛 125125)

摘要:针对固定鸭舵和弹体具有不同的滚转角速度,传统六自由度弹道模型不能有效描述修正弹的飞行状态的问题,为研究固定鸭舵弹道修正弹的弹道特性,将弹丸与修正组件分别作为2个独立刚体建立六自由度弹道模型,分析了两者的运动耦合关系,建立了可表示具有相对滚转向量的七自由度弹道模型。以某型旋转稳定弹为例,通过基于Simulink的弹道仿真,得到了攻角、侧滑角的变化曲线,仿真结果表明该模型能够描述弹丸的弹道特性。

关键词:固定鸭舵;弹道修正;弹道仿真

收稿日期:2014-03-28

基金项目:国防预研

作者简介:张开创(1988-),男,硕士研究生,研究方向为弹药系统设计。E-mail:18333109527@163.com。

中图分类号:TJ43文献标识码:A

ModelingandSimulationofFixed-canardTrajectoryCorrectionProjectile

ZHANGKai-chuang1,LIU Qiu-sheng1,WANG Long2

(1.DepartmentofAmmunitionEngineering,OrdnanceEngineeringCollege,Shijiazhuang050003,China;

2.HuludaoMilitaryRepresentativeOfficeofGeneralArmamentsDepartment,Huludao125125,China)

Abstract:Fixed canard and body of trajectory correction projectile have different roll angular velocity,so the rigid 6D model can’t effectively describe the state of motion in the flight process.Taking projectile and correction system as two rigid bodies separately,6D model was built.The movement relation between the two was studied,and the 7D ballistic model was built.To take a certain spin-stabilized projectile for an example,the variation curves of attack angle and sideslip angle were obtained based on Simulink.The 7D ballistic model can accurately describe the trajectory features through simulation of certain spin-stabilized projectile.

Keywords:fixedcanards;trajectorycorrection;trajectorysimulation

弹道修正弹具有成本低、命中精度高的特点,能大幅度提高作战效能并减小附带毁伤,是当前各国研究的热点。近年来,以美国ATK公司研究的精确制导组件PGK为典型代表,采用固定鸭舵技术对常规弹药进行滚转控制,实现了弹道的二维修正,并成功应用于155mm炮弹和120mm迫击炮弹。用于旋转稳定弹的固定鸭舵,是通过控制固定鸭舵相对于弹体的滚转角速度,使操作舵在大地坐标系中的位置固定,进而产生相应修正力矩实现弹道修正控制。同时,使用固定鸭舵修正组件替代原引信,对现有弹丸改动小,是对库存弹药制导化改造的有效途径。由于固定鸭舵改变弹丸的受力,弹丸的弹道特性也必将发生变化,必须对改装后的弹丸重新建立弹道模型,分析其弹道特性。

1固定鸭舵修正组件结构及修正原理

固定鸭舵修正组件主要有导航与滚转测量模块、弹道解算与控制模块、鸭舵控制模块、安全与起爆控制模块组成。弹丸发射前装定发射点、目标点、气象条件等信息;弹丸发射后,卫星接收机开始接收卫星定位信号,弹载计算机通过卫星定位信号及地磁传感器信号解算弹丸位置、速度姿态等弹道信息;根据弹丸轨迹信息和目标点位置信息按照预先装定的制导算法,形成制导指令;固定鸭舵起停控制模块接收制导指令,然后将转速和固定鸭舵的滚转角输出给执行机构,转换成与之相应的脉宽调制的PWM信号,以实现对固定鸭舵的控制,使固定鸭舵相对惯性坐标系静止,从而产生所需的修正力和力矩,实现弹丸的弹道修正。固定鸭舵修正组件原理示意图如图1所示。

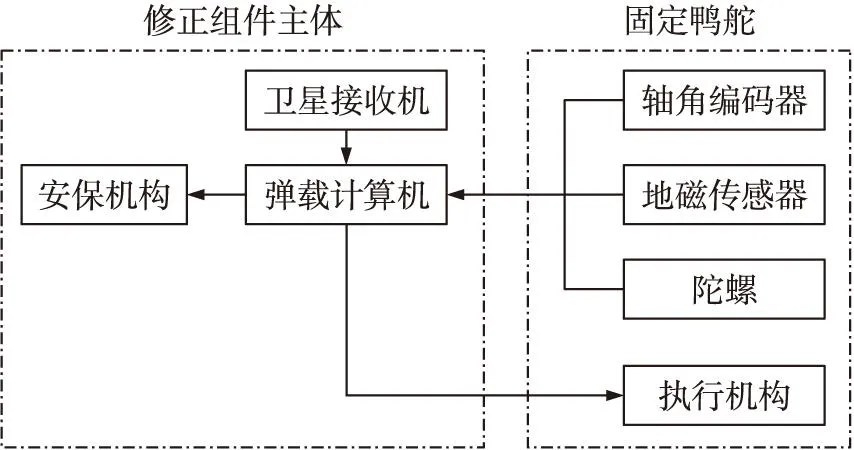
图1　固定鸭舵修正组件原理示意图

固定鸭舵修正组件可分为组件主体和固定鸭舵两部分,两者通过球轴承和轴角编码器连接,可相对滚转运动。固定鸭舵由两对舵片组成,沿弹体轴线成90°正交。舵片固定并具有一定的偏转角。其中,一对舵片偏转角相同但方向不同,构成差动舵,飞行时不形成修正力和力矩;另一对舵片偏转角相同,构成操纵舵,在弹丸飞行过程中通过控制操纵舵的起停位置和角度,形成所需的控制力和力矩[2-3]。

2七自由度模型的建立

2.1　模型建立思路

修正弹由弹体和固定鸭舵2个刚体组成,固定鸭舵修正组件主体通过螺纹连接到弹体上,且与弹体同轴,在弹丸飞行过程中,弹体和固定鸭舵修正组件具有相同的俯仰角速度和偏航角速度。由于差动舵形成的导转力矩作用,固定鸭舵将产生与弹体转动方向相反的转动角速度,而固定鸭舵修正组件的主体将同弹体以相同的角速度旋转。

要准确地描述其运动状态,可以对两部分分别建立相应的六自由度模型,其中2个部分分别受到重力、科氏力、空气动力以及两部分之间的作用和反作用力。因为弹体与固定鸭舵不存在相对位移,所以两部分的质心运动相同,可以作为一个整体建模,此时两部分的作用力与反作用力为内力,质心运动有3个自由度。

对于绕质心转动,弹体和固定鸭舵的偏航、俯仰运动保持一致,同样可以按整体建模,而弹体和固定鸭舵滚转运动不同,应分别建模,因此,绕质心运动有4个自由度。所确立的七自由度分别为:弹丸位移的x,y,z,弹丸转动的偏航、俯仰,弹体绕弹轴的滚转,固定鸭舵绕弹轴的滚转。

2.2　坐标系及角度定义

传统六自由度弹道方程常用坐标系及转换关系见文献。本文引入修正组件体坐标系和修正组件速度坐标系,如图2所示。

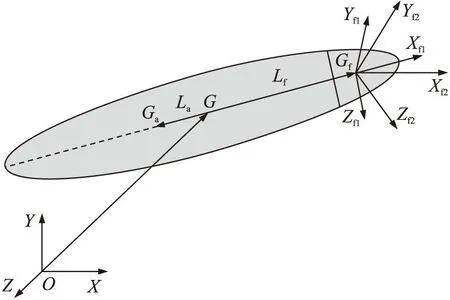
图2　修正组件体坐标系和速度坐标系

修正组件体坐标系OfXf1Yf1Zf1:坐标原点位于修正组件质心,OfXf1轴沿修正组件轴线,OfYf1在修正组件纵向对称面内垂直于OfXf1轴;OfXf1轴、OfYf1轴、OfZf1轴构成右手系。

修正组件速度坐标系OfXf2Yf2Zf2:坐标原点位于修正组件质心,OfXf2轴沿修正组件速度方向,OfYf2在修正组件纵向对称面内垂直于OfXf2轴;OfXf2轴、OfYf2轴、OfZf2轴构成右手系。

定义攻角αf为修正组件速度矢量在修正组件纵向对称面内的投影与OfXf1轴的夹角,OfXf1轴在上时αf为正。

定义侧滑角βf为修正组件速度矢量与修正组件纵向对称面的夹角,速度矢量指向修正组件纵向对称面右侧时βf为正。

φ,ψ,γf,θ,σ分别为修正组件的俯仰角、偏航角、滚转角、修正组件速度倾角和修正组件速度偏角。修正组件所受空气动力通过攻角αf、侧滑角βf和马赫数Ma插值获得的气动参数后经计算得到。

2.3　质心运动方程

2.3.1运动学方程

建立弹丸相对于地面坐标系运动的运动学方程,可确定弹丸相对于地面坐标系的运动轨迹。弹丸质心速度矢量与弹道坐标系OX2轴重合,利用地面坐标系和弹道坐标系的转换关系得:

(1)

式中:ψv为速度偏角。

2.3.2动力学方程

对于刚体,可以应用牛顿第二定律来研究质心移动,即

(2)

在弹道坐标系上建立质心运动的动力学方程的标量形式既简单,又便于分析弹丸运动特性。由矢量的绝对导数和相对导数的关系,式(1)可写为

(3)

式中:Ω为弹体坐标系的角速度。

合外力有空气动力、重力,空气动力沿准速度坐标系上分解,重力在地面坐标系内,根据坐标系的定义和相互间的转换关系,可得:

(4)

式中:Fax,Fay,Faz为弹体所受气动力;Ffx,Ffy,Ffz为固定鸭舵所受气动力。

2.4　绕质心转动方程

2.4.1运动学方程

设固定鸭舵和弹体的滚转角分别为γf,γa,滚转角速度分别为ωfx,ωax。设准弹体坐标系的转动角速度为ω′,则弹丸绕质心转动的运动学方程:

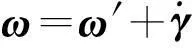
(5)

整理,可得:

(6)

2.4.2动力学方程

准弹体坐标系的转动角速度为

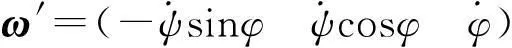
则有:

(7)

式中:L为头部动量矩,Mf为头部力矩。

对固定鸭舵,有:

(8)

式中:Jfx,Jfy,Jfz为固定鸭舵在弹体坐标系内沿各坐标轴的转动惯量;Mfa为固定鸭舵所受的力矩。

对弹体,有:

(9)

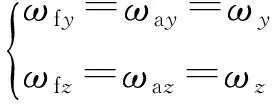
(10)

综上,可得弹丸数学模型。由于固定鸭舵与弹体的滚转角速度不同,需要不同的方程进行描述,故可将该模型称为七自由度弹道模型。

3仿真结果分析

以中大口径加榴炮弹为例,建立七自由度外弹道模型进行弹道仿真,对固定鸭舵转角不进行控制,使其在导转翼面和阻尼力矩以及轴承摩擦力矩等的作用下自由转动,即固定鸭舵自由旋转。假设弹丸质量m=45 kg,初速v0=930m/s,射角θ0=45°,气象条件取标准气象(ton=15°,pon=1.013 Pa,ρon=1.206 kg/m3)。连接固定鸭舵与修正组件尾部的轴承是球轴承,其接触为点接触。两组件间的相对运动会使轴承滚珠发热膨胀,但轴承内外存在间隙且同时有不同程度的膨胀,其摩擦力与摩擦力矩不会有明显的变化,可认为其为常量,取摩擦力矩为0.01 N·m。

图3为仿真所得弹道曲线,从仿真结果可得:弹丸飞行时间为84.1 s,射程24 209.8 m,侧偏206.9 m,最大弹道高8 719.8 m,与制式弹相比,射程、最大弹道高减小。

由于弹丸发射时强大的轴向过载的作用,固定鸭舵修正组件出炮口时随弹体一起旋转,固定鸭舵产生的操纵力和力矩也随着滚转角的改变而不断地变化,进而改变弹体的攻角和侧滑角[7-8]。出炮口后,在导转力矩的作用下固定鸭舵迅速减旋并反向匀速转动,此时将引起攻角、侧滑角的周期性变化。图4、图5分别为攻角、侧滑角曲线。从图中可以看出,攻角、侧滑角的变化曲线与实际分析吻合,且攻角、侧滑角在较小的范围内变化,满足小攻角理论。

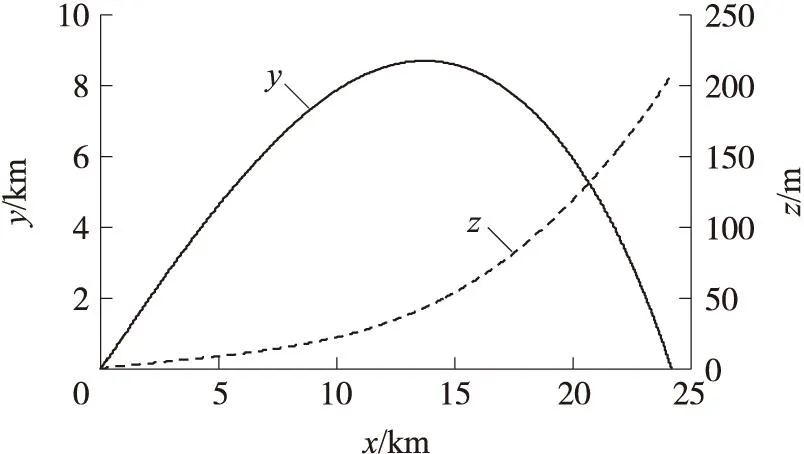
图3　弹道曲线

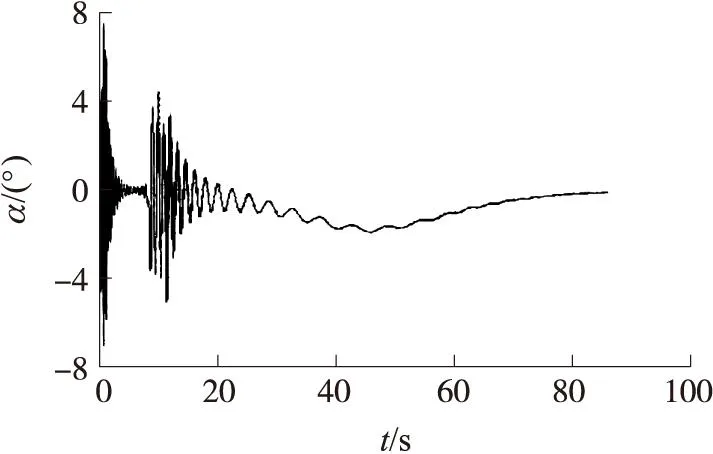
图4　攻角曲线

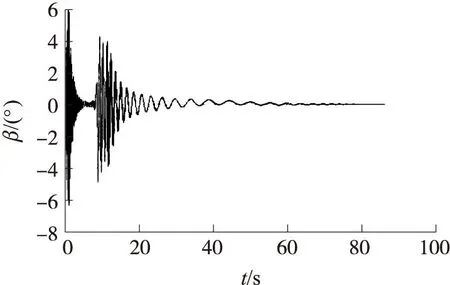
图5　侧滑角曲线

4结束语

本文通过分析固定鸭舵修正组件的结构和工作原理, 提出了建立加装固定鸭舵修正组件的弹丸的弹道模型的思路,运用多刚体理论推导了七自由度弹道模型的数学模型,根据七自由度弹道模型进行了仿真分析,仿真结果表明,该七自由度弹道模型能描述此类弹丸的弹道特性。

参考文献

[1]马宝华.网络技术时代的引信.探测与控制学报,2006,28(6):1-5.

MABao-hua.Fuseinnetworktechnologyera.JournalofDetection&Control,2006,28(6):1-5.(inChinese)

[2]CLANCYJ,BYBEET,FRIEDRIHW.Fixedcanard2-Dguidanceofartilleryprojectile:US,US6981672B2.2006-08-12.

[3]WERNERTP,LEOPOLDF,BIDINOD,etal.Windtunneltestsandopen-looptrajectorysimulationsfora155mmcanardsguidedspinstabilizedprojectile//AIAAAtmosphericFlightMechanicsConferenceandExhibit.Honolulu,Hawaii:IAAA,2008:228-235.

[4]钱杏芳,林瑞雄,赵亚男.导弹飞行力学.北京:北京理工大学出版社,2000.

QIANXing-fang,LINRui-xiong,ZHAOYa-nan.Missileflightmechanics.Beijing:BeijingInstituteofTechnologyPress,2000.(inChinese)

[5]郝永平,孟庆宇,张嘉易.固定翼二维弹道修正弹气动特性分析.弹箭与制导学报,2012,32(3):171-173.

HAOYong-ping,MENGQing-yu,ZHANGJia-yi.Aerody-namiccharacteristicanalysisontwodimensionaltrajectorycorrectorshellwithfixed-wing.JournalofProjectiles,Rockets,Missiles,andGuidence,2012,32(3):171-173.(inChinese)

[6]COSTELLOM.Modelingandsimulationofadifferentialrollprojectile//AIAAModelingandSimulationTechnologiesandExhibit.Boston,MA:AIAA,1998:432-443.

[7]纪秀玲,王海鹏,曾时明.可旋转鸭舵对旋转弹丸纵向气动特性的影响.北京理工大学学报,2011,31(3):265-268.

JIXiu-ling,WANGHai-peng,ZENGShi-ming.CFDpredictionoflongitudinalaerodynamicforaspinningprojectilewithfixedcanard.TransactionsofBeijingInstituteofTechnology,2011,31(3):265-268.(inChinese)

[8]WERNERTP.Stabilityanalysisforcanardguideddual-spinstabilizedprojectiles//AtmosphericFlightMechanicsConference.Chicago:AIAA,2009:182-193.

[9]FRESCONIF,HARKINST.Aerodynamiccharacterizationsofasymmetricandmaneuvering105mm,120mm,and155mmfin-stabilizedprojectilesderivedfromtelemetryexperiments//AIAAAtmosphericFlightMechanicsConference.Portland,Oregon:AIAA,2011:335-341.