基于DHMM 的滚动轴承故障诊断❋

樊 巍，傅 攀，郑晴晴

（西南交通大学 机械工程学院，四川 成都 610031）

0 引言

滚动轴承是旋转机械中的重要元件，它支撑着机械设备，同时设备运行中其他元件的损坏大部分都要传递到轴承上［1］。因此对滚动轴承故障诊断技术的研究对于减少经济损失和重大事故的发生以及保证整个设备的正常运行具有极其重要的意义。本文采用离散隐马尔科夫模型（DHMM）的方法来对滚动轴承进行故障诊断。

1 实验方案

本实验的滚动轴承型号为6205－2RSJEMSKF深沟型轴承，实验中，用电火花制造轴承的3种单一故障形式，分别为内、外圈故障和滚动体故障，故障直径分别为Φ0.177 8mm、Φ0.355 6mm 和Φ0.533 4 mm。以12kHz的采样频率在滚动轴承状态监测台上，分别采集内圈故障、外圈故障、滚动体故障和正常状态运行时的振动数据，从而进行DHMM的训练和识别。本文数据来自Case Western Reserve University，Bearing data center。

2 特征参数提取和PCA降维

本文对监测信号进行分帧处理，然后对各帧信号分别使用时域、频域以及小波包分解的方法提取特征参数。使用主成分分析方法（PCA）对其进行降维处理，去掉了大量的冗余信息，去除特征之间的相关性，减轻了模式分类器的存储量和计算量，更益于模式识别。

鉴于DHMM是按时间序列进行输入的，本文对实验测得的数据先进行分帧处理，然后采用小波包的分析方法对各帧信号进行能量分解［2］。

本文中每种状态共采集30组样本，每组样本采样点数为8 192，共选用120组实验样本进行轴承各状态模型的建模和分类。数据处理过程中，对每个样本信号进行分帧处理，均分为16帧。然后对不同状态下每帧信号进行3层小波包分解，由各频带能量作为特征参数构造特征向量，小波函数选用db4小波，则每帧信号可得到8个特征参数。

由于小波包频带能量所组成的特征向量的维数较高［3］，这就需要采用主成分分析的方法将高维的特征向量进行压缩和优化处理，将特征向量转变为低维，以便于减轻模式分类器的存储量和计算量［4］。

本文保留累计率达到85%的前f个主元，实现了将每帧样本数据8维特征参数降低到了3维。

3 基于DHMM的滚动轴承故障诊断模型

3.1 基于DHMM的滚动轴承故障诊断实现流程

基于DHMM的滚动轴承故障诊断实现流程如图1所示。其中，O＝｛O1，O2，…，OT｝为观测序列，T为样本组数，λ为初始模型。

3.2 DHMM的训练与识别结果

本文将得到的特征参数矢量经Lloyds量化编码，并将其作为观测值序列输入到各状态轴承DHMM中进行学习和训练，同时采用Baum－Welch算法重估修正公式修正模型参数。将隐状态数目设为4，最大迭代步数为20，每种状态下采用5个样本进行训练，得到不同状态下的 DHMM，分别为λ1、λ2、λ3、λ4［5］。利用DHMM重估公式计算当前观测序列的lgP（O/λi）（i＝1，2，3，4）［6］。4种轴承状态下DHMM模型训练每次迭代的对数似然概率随着迭代步数的变化如图2所示。

图1 基于DHMM的滚动轴承故障诊断实现流程

由图2可以看出，4种模型下训练所需的迭代步数分别为：正常状态17步，外圈故障14步，内圈故障20步，滚动轴承故障13步。

图2 各状态下轴承DHMM训练曲线

将从4种状态轴承获取的各10个样本观测值序列分别输入到正常状态DHMM、外圈故障状态DHMM、内圈故障状态DHMM和滚动体故障状态DHMM模型中，计算各模型下的对数似然概率值，输出结果如图3所示 。

图3 各模型下各状态测试样本的输出结果对比

由图3（a）可以看出，将各状态10个样本输入到正常状态DHMM时，经模型计算出的正常状态样本的对数似然概率值都在－200以上，而另外3种状态（外圈故障、内圈故障和滚动体故障）的对数似然概率值均在－600以下，可以很明显地识别出来。同理，由图3（b）、图3（c）、图3（d）可以看出，在外圈、内圈和滚动体故障－200以上可以很好地被识别出来，仅在外圈故障状态识别时有一个出现错误以外，其他识别结果均十分正确，即利用DHMM基本可以很明显地将各状态轴承识别出来。

下面选取不同转速、不同故障直径的滚动轴承振动数据共120组（每种状态轴承各30组数据样本）来验证使用DHMM进行滚动轴承状态识别的准确率，其统计结果如表1所示。

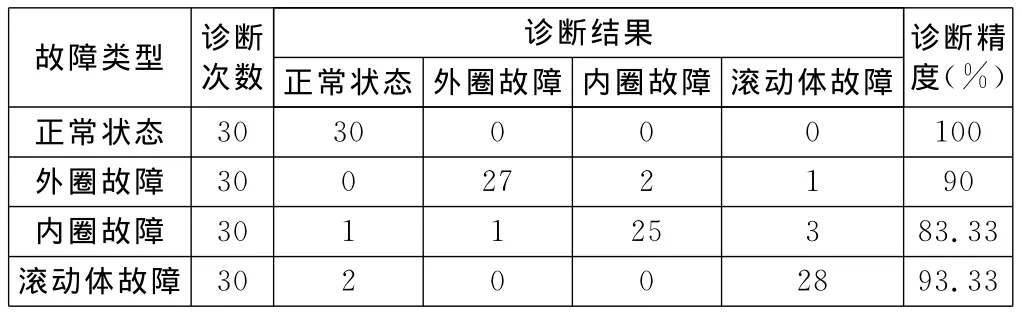
表1 4种状态轴承各30组样本DHMM诊断的统计结果

由以上实验结果可知，利用较少的样本（本文各轴承状态仅用5个样本）训练得到的各个状态的DHMM模型，可以很好地将各轴承状态识别出来。通过表1可以看出，对各状态共120组样本进行DHMM识别统计，平均识别率达到90%，结果是非常

理想的。

4 结束语

DHMM作为一种新型的识别模型的方法，特别适合与振动信号类似的非平稳、信息量大以及特征重复不佳的场合。本文以滚动轴承为研究对象，取振动信号为监测信号，验证了该模型只需要少量的训练样本就能很快完成模型训练，并且在进行不同轴承故障识别时具有较高分类和识别精度。

［1］樊永生.机械设备诊断的现代信号处理方法［M］.北京：国防工业出版社，2009.

［2］陈季云，陈晓平.基于小波包分析的滚动轴承故障特征提取［J］.微计算机信息，2007，23（4）：192－193，219.

［3］Hotelling H.Analysis of a complex of statistical variables with principal components［J］.Journal of Educational Psychology，1933，24（6）：417－441.

［4］李磊.基于PCA降维的SVM人脸快速检测方法［J］.青岛科技大学学报，2010（5）：1－3.

［5］Jun Du，Yu Hu，Hui Jiang.Boosted mixture learning of gaussian mixture hidden markov models based on maximum likelihood for speech recognition［J］.IEEE Transactions on Audio，Speech and Language，2011，19（7）：2091－2100.

［6］陆汝华，杨胜跃，朱颖，等.基于DHMM轴承故障音频信号诊断［J］.计算机工程与应用，2007（17）：137－143.