基于Lem pel-Ziv复杂度和经验模态分解的癫痫脑电信号的检测方法
夏德玲, 孟庆芳, 牛贺功, 魏英达, 刘海红(.济南大学信息科学与工程学院,山东省智能计算网络重点实验室,济南 500;.青岛理工大学汽车与交通学院,青岛 6650)
基于Lem pel-Ziv复杂度和经验模态分解的癫痫脑电信号的检测方法
夏德玲1, 孟庆芳1, 牛贺功2, 魏英达1, 刘海红1
(1.济南大学信息科学与工程学院,山东省智能计算网络重点实验室,济南 250022;
2.青岛理工大学汽车与交通学院,青岛 266520)
癫痫脑电信号是非平稳、非线性的,根据此特性我们提出一个基于Lempel-Ziv复杂度和经验模态分解(EMD)的癫痫脑电信号的检测方法,首先将癫痫脑电信号用EMD分解,再分别计算每阶固有模态函数(IMF)的复杂度,最后将得到的复杂度作为特征进行检测.实验用波恩数据库来评估提出的方法.结果表明,该方法检测准确率可达到95.25%,具有准确率高、适应性强等优点.
Lempel-Ziv复杂度;经验模态分解;癫痫脑电信号;准确率
0 引言
癫痫是目前最普遍的脑部疾患之一,其发病原因复杂,大多数是与神经元胶质细胞病变从而导致神经系统失调有关[1-2].目前对这种疾病的分析主要是由人工完成,如观察脑电图等;但是由于脑电信号持续时间长、复杂度高、高度非线性,人工检测误差较大并且此病突发性比较强难以预测.因此,提出一种高效的自动检测算法不仅有利于减轻医务人员的工作量,而且其在推动临床应用中的贡献将是巨大的.
1985年,Babloyantz[1]等人将非线性动力学和混纯理论应用于脑电信号的分析中,为脑电的研究开辟了新的途径.与此同时,许多非线性的方法被提出来用于癫痫的研究.在这些非线性参数中,关联维数方法可以区分正常脑电和癫痫脑电[2],而且已经被应用于脑电图中不同生理和病理状态的研究中[3-4];李亚普诺夫指数方法主要是根据非线性系统对初始扰动的敏感度不同来研究的,而脑电信号也是非线性的[5-6];用熵来检测癫痫[7];分形维数及其改进的算法用来区别正常的和癫痫两种脑电信号[8-9].
复杂性度量方法是由Lempel和Ziv[10]提出的,其出现新模式的速率与给定序列的长度有关.由于该Lempel-Ziv算法操作简单等优点,被广泛应用到生物医学信号中,例如心电[11]、肌电[12]、颅内压信号[13]以及脑电[14]等.在大多数的研究中,都是根据阈值将信号转换成一个二进制序列.
经验模态分解(EMD)是由Huang等人在1998年提出的一种信号分析技术,它能自适应的把任何时间序列分解成一组独立振荡模式函数,该函数被定义为Instrinic Mode Functions,简称IMF.与小波变换相比, EMD有其内在的优势,因为基本的分解函数是由数据本身的属性决定的.也就是说,EMD分解信号不需要将先验知识嵌入到数据序列里[15].最近的研究证明,EMD在相空间同步、分析复杂吸引子等有重要的作用[16].但不幸的是,EMD缺少一个坚定的理论框架和存在一些缺陷,像极点的位置、极值插值、筛选停止准则等[17].尽管一些研究在试图缓解上述问题,但EMD基本的理论仍需要巩固来得到更精确、更可靠的结果.
我们提出一个基于Lempel-Ziv复杂度和EMD的新方法用来检测和识别癫痫,将癫痫信号分解成五层固有模态函数(IMFs),然后将其作为特征来计算复杂度.该方法展示了良好的性能,如较高的准确率、操作简单等.此外,相比于只用Lempel-Ziv复杂度方法,该方法更适合应用于患有癫痫病的病人的诊断中,挽救其生命.
1 基于Lempel-Ziv复杂度的癫痫脑电算法
根据混沌动力学理论,当一个系统从一个平稳状态转化为一个非平稳状态,系统的复杂度将会发生巨大的变化.研究采用基于二值化的Lempel-Ziv(LZ)复杂度算法,它是一种用于度量随着序列长度的增加而新模式也增加的算法.该算法的实质是不断比较对于给定的序列S和Q,判断字符串Q是否是SQ的子串;如果是,则添加次数c维持不变,否则c加一.其具体算法如下[10-11]:
1)根据给定长度的信号计算其阈值,根据阈值将癫痫信号转化为一个二进制序列;
2)设给定的序列为S和Q.用SQ表示把S,Q两个符号串拼接成的总字符串,SQπ表示把SQ中最后一个字符删去所得的字符串(π表示去掉它前面的符号串的最后一个符号的操作).假设v(SQπ)为SQπ中所有不同的子序列.开始的时候,c=1,S=s(1),Q=s(2),因此SQπ=s(1);
3)一般的,Q =s(1),s(2),…,s(t),Q=s(t+1),于是SQπ =s(1),s(2),…,s(t);如果Q属于v(SQπ),则Q就是SQπ的一个子序列,而不是一个新的序列.则另Q=s(t+1),s(t+2),继续观察;
4)如果Q不属于v(SQπ),则用添加的操作将s(t+1)加到SQπ后面,即SQπ=s(1),s(2),…,s(t), s(t+1),添加次数c加一(初始值c=1);
5)重复步骤3)、4),直到Q已包含给定序列的最后一个符号,则程序结束.
设c(n)为序列的LZ复杂度,n为序列的长度,则二进制的LZ复杂度为c(n)=c log(n)/(n log2).脑电信号的LZ复杂度反映了脑电信号的变化,可以揭示大脑的相关规律[18].
2 基于EMD的癫痫脑电算法
经验模态分解(EMD)是在1998年首次被提出的,是将信号分解成一组带宽有限的子带信号.它是一种用来分析非线性、非平稳信号的技术,已经被成功的应用于滤波、坏点检测、生物信号分析、信息监测等[15].相比于其他非平稳信号处理方法,如小波分析、Wigner-Ville分布等,EMD更直接、自适应能力更强.
对于一个给定的癫痫脑电信号x(t),余量信号r(t),n=0,进行EMD分解的步骤如下:
1)找出x(t)的所有极值点,包括极大值和极小值;
2)用插值法对极小值点形成下包络,用emin(t)表示;对极大值形成上包络,用emax(t)表示;
3)计算信号x(t)的均值
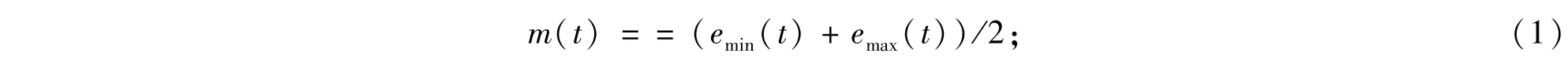
4)对给定信号x(t),抽离细节信息,定义为
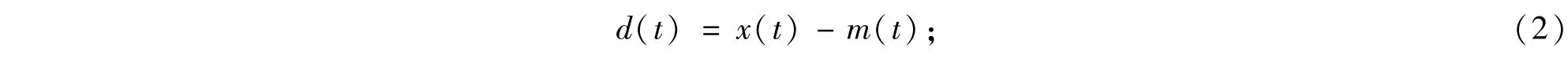
5)求d(t)的均值d′(t).如果d′(t)=0,或者满足某种停止准则则停止迭代.此时,n=n+1,IMFn=d(t),继续步骤6);如果不满足x(t)=d(t),重复1)-5)步骤;
6)令t(t)=r(t)-IMFn,如果r(t)是一个单调函数,则停止筛选过程;否则,令x(t)=r(t),回到步骤1).不断重复以上过程,极值点的数量将会越来越少,整个分解过程会产生有限个模函数(IMF).因此,可将信号x(t)表示成:
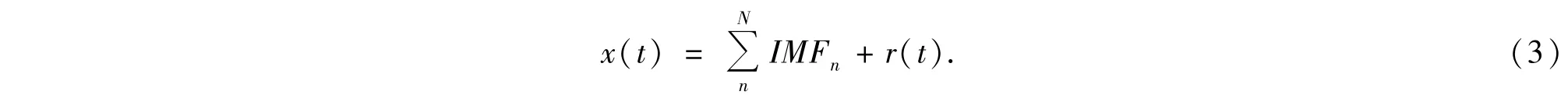
本文将x(t)经EMD分解为五阶IMF分量,因此N=5.
3 以Lempel-Ziv复杂度为特征的癫痫脑电检测方法
根据癫痫脑电信号的非线性特征,将其用EMD方法分解成五阶IMF分量,然后利用Lempel-Ziv(LZ)复杂度算法计算每阶IMF分量的复杂度,并以此特征作为分类,算法流程如图1所示.EMD就像一个高通滤波器,它首先迅速地改变复合信号的分量.IMF1包含信号的最高频率,而残留的信号里则包含信号的最低频率.脑电信号的特征主要与前五个IMFs分量有关,因此本文选用EMD的五阶IMF分量.由于各分量种所含的有用脑电信号不同,而间歇期脑电和发作期脑电的LZ复杂度不同;因此用以LZ复杂度为特征检测发作期和间歇期脑电.

图1 癫痫脑电检测流程图Fig.1 Flow chart of epiletic detection
4 实验结果与分析
本文采用的数据来自德国波恩癫痫研究室临床采集的脑电数据库,用到D组(癫痫患者未发作的间歇期脑电)和E组(发作时的癫痫脑电)数据集;其中D组数据集用F表示,E组数据集用S表示.实验选取F 和S数据各200个样本,每个样本长度为1 000点数据.为了便于评价,我们用到三个指标:敏感度(sensitivity)、特异性(specificity)和准确率(accuracy).假设算法为检测癫痫患者未发作的间歇期脑电F的算法,则计算公式如下

式子中,TP表示F判断为F的数目,FN表示F判断为S的数目,TN表示S判断为S的数目,FP表示S判断为F的数目.本文中,为了便于说明本文提出的算法检测F和S的效果,我们用准确率的大小来评判,即在选定的样本,得到Lempel-Ziv复杂度的特征区间,并把这些特征区间均匀分割成n等分(n为样本的个数),其阈值设为thi(i=1,…,n),逐一遍历直到准确率为最大,此时的阈值thi即为我们本文用到的阈值.
图2是癫痫发作间歇期和发作期的复杂度分布图,从图中我们可以看出仅基于复杂度这个特征来检测癫痫发作间歇期和发作期是非常困难的,其原因之一是:癫痫发作间歇期和发作期这两种信号波形会交叉,从而导致区分效果不好;原因之二是因为癫痫信号中混有大量的噪声,如基线漂移、工频干扰等,噪声的存在也使得结果不理想.
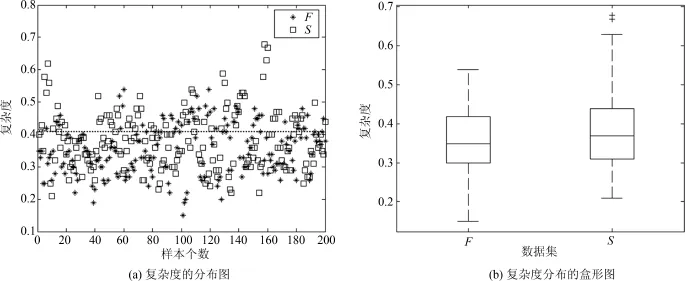
图2 癫痫发作间歇期和发作期的LZ复杂度分布图Fig.2 (a)LZ complexity of seizures of interical and ictal;(b)Box-plot of(a)
为了提高检测精度,考虑到脑电信号的频率范围在0.5 Hz~100 Hz之间,而基线漂移的频率大约在0.15 Hz~0.3 Hz之间,工频干扰是由50 Hz交流电产生的,研究用EMD技术将脑电信号分解成五阶IMF分量,这样噪声大约被分解到低频分量里边,高频分量里边有用信号占的比例多,因此再计算高频分量的复杂度其结果将比仅用复杂度的结果好.表1是本次实验的结果,从表中可以得出结果与理论分析基本吻合.
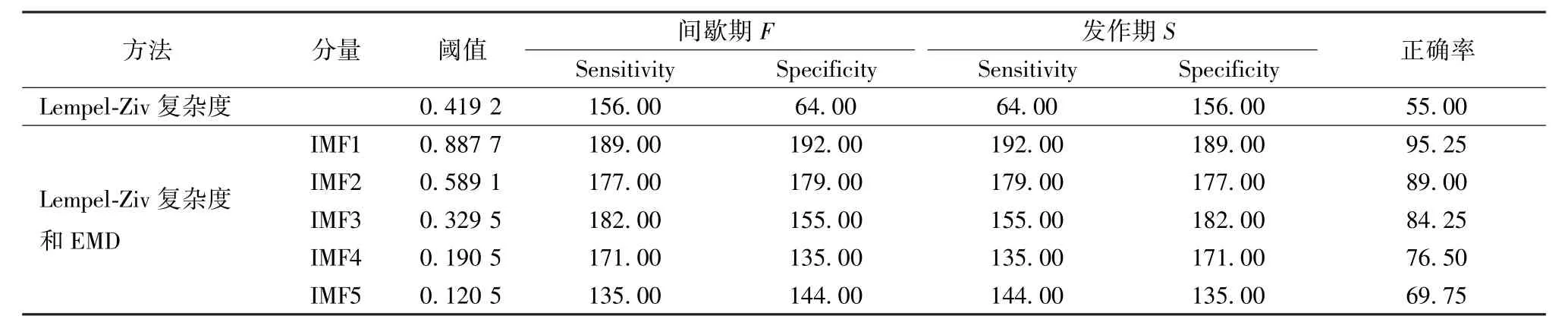
表1 用Lempel-Ziv复杂度和EMD检测方法的实验结果Table 1 Classification of interical and ictal EEG using EMD and com plexity analysis
运用EMD算法,将癫痫发作间歇期和发作期信号分解成五阶IMF分量,其波形如图3所示.图4是IMF1分量复杂度的分布图,检测准确率可高达95.25%,因此所提出的检测方法比较好.由表1,IMF3分量以后效果就不好了,其原因主要是癫痫脑电信号频带宽度相对比较窄,和噪声的频带重合的比较多,因此IMF4和IMF5分量的区分结果并不好.

图3 癫痫发作间歇期和发作期的五阶IMF分量Fig.3 A segment of EEG signals:(a)the first five IMFs of interical EEG;(b)the first five IMFs of ictal EEG
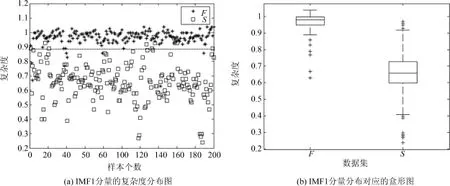
图4 癫痫发作间歇期和发作期的IMF1分量的复杂度分布Fig.4 (a)Complexity of the first IMF1 of interical EEG and ictal EEG;(b)Box-plot of(a)
由此我们可以推断,癫痫脑电信号(间歇期和发作期)经过EMD分解以后,由于各分量种所含的有用脑电信号不同,而间歇期脑电和发作期脑电的LZ复杂度不同.因此,用本文所提出的方法来检测癫痫脑电的发作期和间歇期的效果要远远好于仅用LZ复杂度方法来检测的,由表1可见.
5 结论
利用癫痫脑电信号的非平稳特性,结合混沌动力学理论,提出了一种基于Lempel-Ziv复杂度和EMD的癫痫脑电自动检测方法,该方法有适应性强、误检率低等优点.此外,相比于Lempel-Ziv复杂度的方法,该方法更适合于癫痫病的诊断,更能挽救病人的生命.
[1] Babloyantz A,Salazar JM.Evidence of chaotic dynamics of brain activity during the sleep cycle[J].Phys Lett A,1985,3 (111):152-156.
[2] Wang X Y,Meng J,Qiu TS.Research on chaotic behavior of epilepsy electroencephalogram of children based on independent component analysis algorithm[J].JBiomed Engin,2007,24(4):835-841.
[3] Jeong J,Kim D J,Chae JH,Kim SY,Ko H J,Paik IH.Nonlinear analysis of the EEG of schizophrenics with optimal embedding dimension[J].Med Eng Phys,1998,20:669-676.
[4] Ferri R,Alicata F,Del Gracco S,Elia M,Musumeci SA,StefaniniM C.Chaotic behavior of EEG slow-wave activity during sleep[J].Electroenceph Clin Neurophysiol,1996,99:539-543.
[5] Swiderski B,Osowski S,Rysz A.Lyapunov exponent of EEG signal for epileptic seizure characterization[J].Chaos,1995, 5(1):82~87.
[6] Li Shufang,Zhou Weidong,Yuan Qi,Geng Shujuan,Cai Dongmei.Feature extraction and recognition of ictal EEG using EMD and SVM[J].Comput Blol Med,2013,43:807-816.
[7] Kannathal N,Choo M L,et al.Entropies for detection of epilepsy in EEG[J].Computer Methods Progr Biomed,2005,80 (3):187-194.
[8] Accardo A,Affinito M,CarrozziM,Bouquet F.Use of the fractal dimension for the analysis of electroencephalographic time series[J],Biol Cyber,1997,77:339-350.
[9] Easwaramoorthy D,Uthayakumar R.Improved generalized fractal dimensions in the discrimination between healthy and epileptic EEG signals[J].JComput Sci,2011,2(1):31-38.
[10] Lempel A,Ziv J.On the complexity of finite sequences[J].IEEE T Inform Theory,1976,IT-22(1):75-81.
[11] Zhang H X,Zhu Y S,Wang Z M.Complexity measure and complexity rate information based detection of ventricular tachycardia and fibrillation[J].Med Blol Eng Comput,2000,38:553-557.
[12] Zhang X,Roy R J,Weber E.EEG complexity as ameasure of depth of anesthesia for patients[J].IEEE TBIO-MED ENG, 2001,12:1424-1433.
[13] Hornero R,Aboy A,Abósolo D.Analysis of intracranial pressure during acute intracranial hypertension using Lempel-Ziv complexity:further evidence[J].Med Blol Eng Comput,2007,45:617-620.
[14] Radhakrishnan N,Gangadhar BN.Estimating regularity in epileptic seizure time-series data:A complexity-measure approach [C]∥IEEE Eng Med Biol 1998,17:89-94.
[15] Huang N E,Shen Z,Long S R,Wu M C,Shih H H,Zheng Q,Yen N C,Tung C C,Liu H H.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis[D].Proc R Soc Lond A,1998, 454:903-995.
[16] Chavez M,Adam C,Navarro V,Boccaletti S,Martinerie J.On the intrinsic time scales involved in synchronization:a datadriven approach[J].Chaos,2005,15:023904.
[17] Rato R T,Ortigueira M D,Batista A G.On the HHT its problems,and some solutions[J].Mech Syst Signal Process,2008, 22:1374-1394.
[18] Zhang Dianzhong.Coarse grainingmethod in Lempel-Ziv complexity arithmetic[J].Chinese JComput Phys,2008,25(4):499 -504.
Classification of Epilepsy Based on Lem pel-Ziv Com plexity and EMD
XIA Deling1, MENG Qingfang1, NIU Hegong2,WEIYingda1,LIU Haihong1
(1.School of Information Science and Engineering,University of Jinan,Shandong Provincial Key laboratory ofNetwork Based Intelligent Computing,Jinan 250022,China;2.Qingdao Technological University,College ofAutomobile and Transportation,Qingdao 266520,China)
Taking non-stationary and nonlinearity of epilepsy signals into consideration,we proposed a method for detection of epilepsy,based on Lempel-Ziv(LZ)complexity and empiricalmode decomposition(EMD).EMD first decomposed epilepsy signals into a set of intrinsicmode functions(IMFs).Then calculated complexity of each IMF.Bonn dataset was utilized for evaluating the method.Experimental results showed that the highest accuracy could be achieved to 95.25%.It has advantages of high accuracy, strong adaptability and so on.
Lempel-Ziv complexity;empiricalmode decomposition(EMD);epilepsy signals;accuracy
1001-246X(2015)06-0709-06
TP301.6
A
2014-11-24;
2015-02-07
国家自然科学基金(61201428,61070130)资助项目
夏德玲(1989-),女,硕士,主要从事生物时间序列分析、信智能信息处理研究,E-mail:xiadeling@yeah.net

