重力场和强磁场中费米气体的热力学性质

田青松, 门福殿通讯作者：门福殿,E-mail：menfudian＠163.com, 陈新龙（中国石油大学（华东）理学院,山东青岛 266580）

重力场和强磁场中费米气体的热力学性质

田青松, 门福殿∗∗通讯作者：门福殿,E-mail：menfudian＠163.com, 陈新龙
（中国石油大学（华东）理学院,山东青岛 266580）

基于半经典近似,研究重力场和强磁场共存下费米气体的热力学性质,通过理论解析和数值模拟分析强磁场背景下重力场对系统热力学性质的影响.研究表明：与单纯强磁场相比,重力场的引入使能量及化学势都降低.随温度的上升,重力场对化学势的影响逐渐放大；对热容的影响有极大值.重力场使系统的热容随磁场的振荡几乎不变、使化学势的振荡中心下移.

重力场；强磁场；费米气体；热力学性质

0 引言

近年来,研究外势及相互作用同时对热力学系统的影响成为热点课题.特别是对谐振势约束下的量子系统进行了较为深入的研究,取得了一系列的成果[1－10].磁场是一种重要的约束[11],对于强磁场约束下费米气体的性质有不少研究.如,文献[12]研究了强磁场中弱相互作用费米气体的稳定性.文献[13]研究了强磁场中超冷费米气体的相对论效应.文献[14]研究了强磁场中费米气体的稳定性及顺磁性.文献[15]研究了强磁场中弱相互作用费米气体的热力学性质.文献[16]基于准经典近似研究了强磁场中高温费米气体的统计性质.但在强磁场和重力场共同约束下的费米气体的热力学性质尚无人研究.众所周知,重力场是一种客观存在的势场,尽管在微观领域中重力的强度相对较弱,然而研究表明,重力的量子效应的确存在[17],再加上实验手段愈来愈精细,测量愈来愈精准,因而在理论研究中需考虑重力场对低温费米气体统计性质的影响.尤其对有精细结构及超精细结构的费米系统（如6Li原子系统,它有6个超精细能态）,重力场的影响是不可忽略的.因此研究双场（磁场和重力场）约束下的费米系统有实际意义.相对于强磁场,重力场对系统热力学量的贡献较小,但其理论研究的结果对于掌控强磁场背景下系统的性质是重要的.如,利用磁场作为外部控制手段来实现磁场Feshbach共振以改变原子间的散射长度的实验,当要实现某一高精度时,有必要在磁场背景下考虑重力场的修正.本文基于半经典近似方法,通过泊松公式解析双场共存下费米系统的低温热力学势函数,在此基础上运用热力学关系和数值模拟方法分析强磁场背景下重力场对总能、热容、化学势的影响.

1 同时考虑重力场和强磁场情况下的热力学势函数

考虑自旋量子数s＝1/2、静止质量为m的费米子构成的系统,处在沿z轴方向的均匀磁场以及重力加速度为g、高度为z的重力场中.利用半经典近似的方法,参考文献[19],则费米子在磁场和重力场共存条件下的总能可表示为

式中σ＝he/4πmc为玻尔磁子,n＝0,1,2,3,…,为量子数,mgz为重力场作用项.

根据文献[18],当n,pz给定时,在Δpz区间内的量子态数为

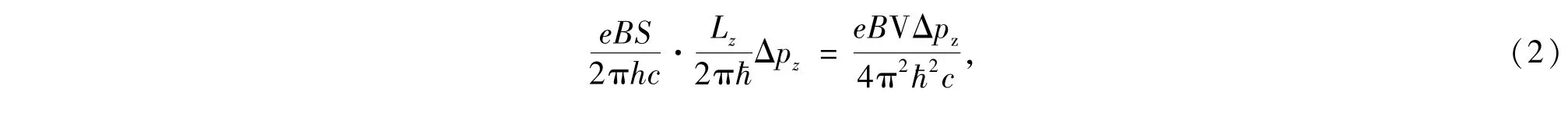
其中Lz为粒子在z方向的运动区域的尺度,令Lz＝Δz,即粒子z方向的运动尺度在有限范围内为一可变的量.再考虑自旋,则粒子在ΔpzΔz区间的量子态数为

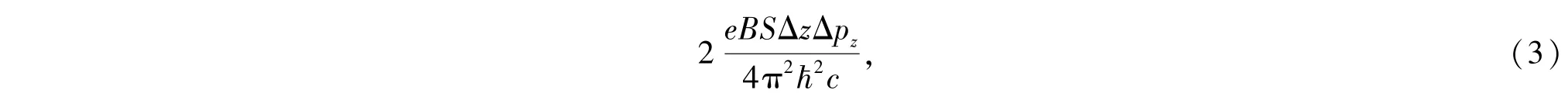
再根据文献[19],pz是在磁场方向的动量,取－∞到∞的连续值,z取0到z的有限连续值,对于每个给定的n在间隔d pzd z中的态的数目是

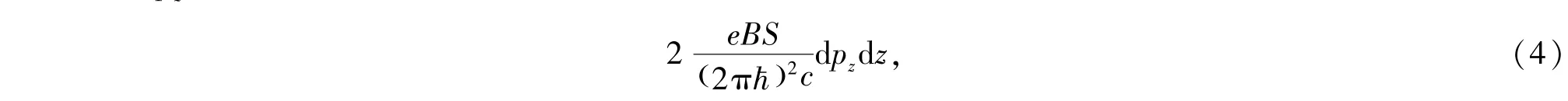
则系统的热力学势函数可表示为

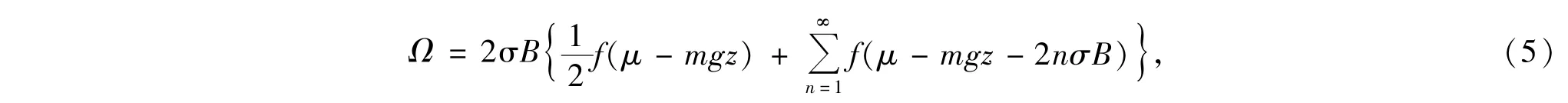
其中

利用泊松公式[17],则（5）式可表为

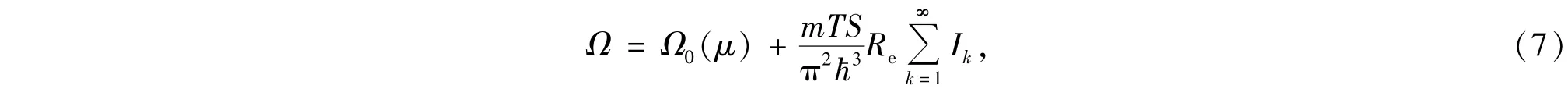
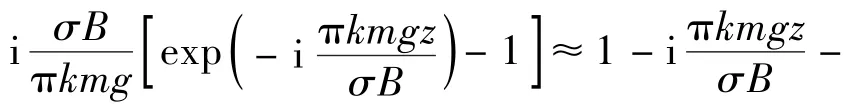
其中ΩB＋G（μ）为磁场和重力场的影响项.经计算,有

式中Ω0＝（mσB）3/2TS/π3h－3,λ＝πmg/2σB,a＝eμ/T,b＝1＋eμ/T,d＝cosα,f＝sinα,w＝sinhβ.

2 热力学量的解析式

运用热力学关系

其中U,C,u分别是系统的总能、热容、化学势.在低温下（T≪TF,TF为自由系统的费米温度）,忽略温度对化学势的微弱影响,即取自由系统的化学势为μ≈εF＝h2（3π2n）2/3/2m,分别得系统的总能、热容量、化学势的重力场和磁场影响项：

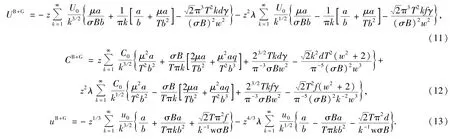
式（11）～（13）中,U0＝m3/2（σB）5/2S/π3h－3,C0＝（mσB）3/2S/π3h－3,γ＝coshβ,u0＝m1/2（σB）3/2/（3π2N/S）1/3πh－, q＝1－eμ/T,β＝π2kT/σB,α＝πkμ/σB－π/4.λ,a,b,d,f,w与式（9）中的形式一样.

3 数值模拟与分析

3.1 热力学量随温度的变化

考虑强磁场条件T≤σB≪μ,令μ＝xσB,T＝yσB（x≫1,0＜y≤1）则有

式（14）～（16）中U0,C0,u0,λ,d,f,w,γ与（11）～（13）式中的形式一样,只是a＝ex/y,b＝1＋ex/y,q＝1－ex/y,α＝πkx－π/4,β＝π2ky.根据式（14）～（16）,以国际单位制为标准取εF～10－24,σB～10－2εF, N/S～1021,S＝1,m～9.11×10－31,x＝100、101、99、98,即μ＝100σB、101σB、99σB、98σB,g～10,z取适当值做图1～3（y＝T/σB＝[0～1]）.在以下所有图中,虚线标识单纯强磁场下的热力学量,实线标识磁场与重力场共存下的热力学量.式（9）、（11）～（13）中第一项（第一个大括号）是单纯强磁场下的热力学量,第二项（第二个大括号）为强磁场背景下引入重力场后的热力学量.如果mgz＝0,则以上各式便回到单纯强磁场的情况,这使得结果具有普遍意义.

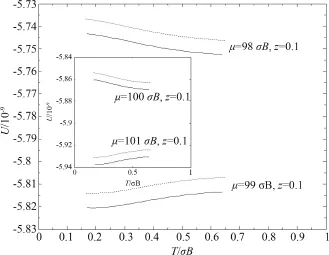
图1 能量随温度的变化Fig.1 Energy varies with temperature

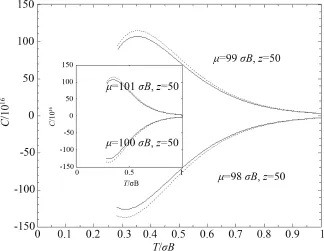
图2 热容随温度的变化Fig.2 Heat capacity varieswith temperature

3.2 热力学量随磁场的变化

再令σB＝pμ,T＝10－2TF≈10－2μ,即x＝1/p,y＝10－2/p,x/y≈102,U0＝m3/2μp（ ）5/2 S/π3h－3, C0＝（mμp）3/2S/π3h－3,u0＝m1/2（μp）3/2/（3π2N/S）1/3πh－,λ＝πmg/2μp,a＝102,b＝1＋e100,α＝πk/p －π/4,β＝10－2π2k/p.d,f,w,γ与（11）～（13）式中的形式一样,并经简化后有

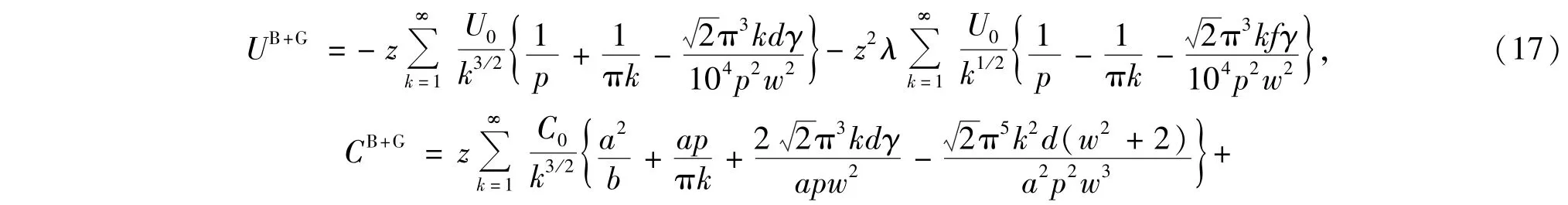
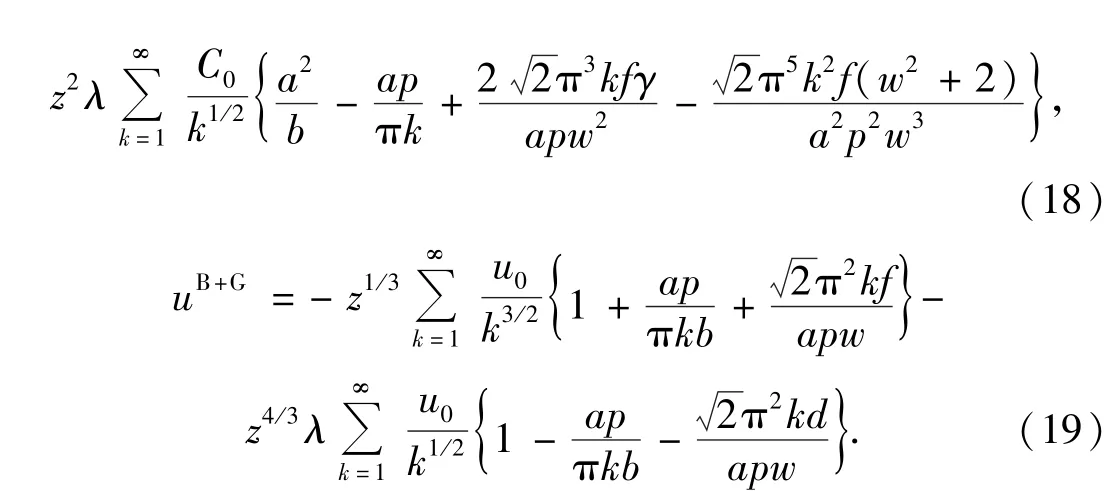
图3 化学势随温度的变化Fig.3 Chemical potential varies with temperature

根据式（17）～（19）,令μ～10－24,p＝σB/μ＝[0～0.09],z取适当值做图4～6.

3.3 分析与讨论

由图1～3可知,从能量随温度的变化情况看,无论μ为偶数（如μ＝100σB）还是奇数（如μ＝101σB）,与无重力场（即单纯强磁场）相比,重力场的加入使能量整体有所降低,但能量随温度的变化特征不变.从热容随温度的变化情况看,当μ为偶数时,与单纯强磁场相比,重力场的引入使热容量升高；当μ为奇数时,与单纯强磁场相比,重力场的加入使热容量降低.无论μ为偶数还是奇数,随着温度的升高重力场对热容的影响都逐渐减弱,且都有极大值.从化学势随温度的变化情况看,无论μ为偶数还是奇数,与单纯强磁场相比,重力场的加入使化学势下降,并且随着温度的增加,这种影响被放大.

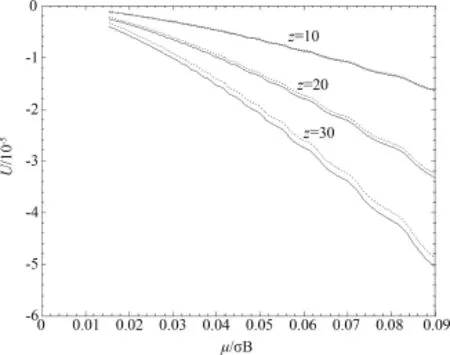
图4 能量随磁场的变化Fig.4 Energy varieswithmagnetic field

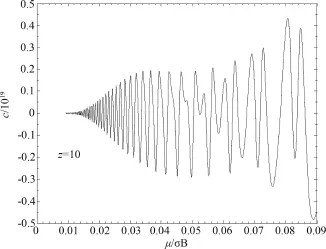
图5 热容随磁场的变化Fig.5 Heat capacity varies with magnetic field

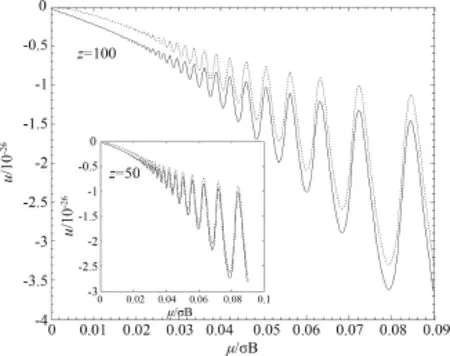
图6 化学势随磁场的变化Fig.6 Chemical potential variesmagnetic field

图4～6表明,从能量随磁场的变化情况看,重力场没改变磁场对能量影响的趋势,只是使系统的能量更低.并且高度z值越大,重力场影响越明显.磁场与重力场对热容的影响随磁场的变化呈现不规则振荡,且重力场的引入对热容的影响几乎为零.就化学势的影响随磁场的变化情况看,与单纯强磁场相比,重力场的引入使化学势的振荡幅度几乎不变,振荡中心下移.且随高度z的增加,影响越明显,相位几乎不变.

4 结论

基于强磁场条件,根据半经典近似引入重力场,用理论解析和数值模拟的方法研究了重力场和强磁场共存条件下费米气体的热力学性质,分析了强磁场背景下重力场对能量、热容和化学势的影响.研究表明,从热力学量随温度的变化看,与单纯强磁场相比,重力场的引入使能量和化学势下降；当自由系统的化学势为偶数时,重力场升高了热容量；当自由系统的化学势为奇数时,重力场降低了热容.从热力学量随磁场的变化看,重力场没改变磁场对能量、热容及化学势影响的趋势,只是使系统的能量更低、热容的振荡几乎不变、化学势的振荡中心下移.

[1] LiM Z,Yan Z J,Chen JC,etal.Thermodynamic properties of an ideal Fermigas in an external potentialwith U＝brtin any dimensional space[J].Physical Review A,1998,58（2）：1445－1449.

[2] Li M Z,Lin H S,Chen L X,etal.Chemical potential and heat capacity of an ideal Fermigas trapped in a harmonic potential in any dimensional space[J].Journal of Xiamen University（Natural Science）,1998,37（4）：498－502.

[3] Noronha JM B,Toms D J.The specific heat of a trapped Fermigas：an analytical approach[J].Physics Letters A,2000, 267（4）：276－280.

[4] Butts D A,Rokhsar D S.Trapped Fermigases[J].Physical Review A,1997,55（6）：4346－4350.

[5] Bruun G M,Burnett K.Interacting Fermigas in a harmonic trap[J].Physical Review A,1998,58（3）：2427－2434.

[6] Oliva J.Density profile of the weakly interacting Fermi gas confined in a potential well：Nonzero temperature[J].Physical Review B,1989,39（7）：4204－4208.

[7] Roth R,Feldmeier H.Effective s-and p-wave contact interactions in trapped degenerate Fermigases[J].Physical Review A, 2001,64（4）：043603（1）－（17）.

[8] Su G Z,Chen L X.Thermodynamic properties of a weakly interacting Fermi gas[J].Acta Phys Sin,2004,53（4）：984－990.

[9] Su G Z,Chen JC,Chen L X.Low-temperature behavior of a weakly interacting Fermi gas trapped in a power-law potential [J].Physics Letters A,2003,315（1－2）：109－119.

[10] Wu D P,Men FD,Liu H.Ground state of Bose-Einstein condensation in F-G-H method[J].Chinese JComput Phys,2009, 26（6）：942－948.

[11] Mou SY,Zhang XW,Dai B.Two-dimensionalelectronic structure in a periodicmagnetic field[J].Chinese JComput Phys, 2014,31（2）：237－242.

[12] Men F D,Tian Q S,Chen X L.Stability of a weakly interacting Fermi gas in a strongmagnetic field[J].Acta Phys Sin, 2014,63（12）：120504（1）－（3）.

[13] Men F D,He X G,Zhou Y,et al.Relativistic effect of ultracold Fermi gas in a strongmagnetic field[J].Acta Phys Sin, 2011,60（10）：100502（1）－（4）.

[14] Men F D,Wang H T,He X G.The stability and paramagnetism of Fermi gas in a strongmagnetic field[J].Acta Phys Sin, 2012,61（10）：100503（1）－（5）.

[15] Men F D,Wang B F,He X G,et al.Thermodynamic properties of a weakly interacting Fermi gas in a strongmagnetic field [J].Acta Phys Sin,2012,61（10）：080501（1）－（5）.

[16] Men F D,He X G,Liu H,et al.Statistics of Fermi gas in a strongmagnetic field at high temperatures with quasi-classical approximations[J].Chinese JComput Phys,2011,28（6）：895－900.

[17] Nesvizhevsky V V,Borner H G,et al.Quantum states of neutrons in the earth's gravitational field[J].Nature,2002,415：297－299.

[18] Landau L D,Lifshitz EM.Quantum mechanics（Non-relativistic theory）[M].3rd ed.Oxford：Pergamon Press,1980.455 －463.

[19] Landau L D,Lifshitz EM.Statistical physics：Part I[M].3rd ed.Oxford：Pergamon Press,1980.171－177.

Thermodynam ic Properties of Ferm i Gas Trapped in Both Gravity Field and M agnetic Field

TIAN Qingsong, MEN Fudian, CHEN Xinlong
（College ofScience,China University of Petroleum（East China）,Qingdao 266580,China）

With semi-classical approximation,thermodynamic properties of Fermigas trapped in both gravity field and magnetic field are studied.By using theoreticalanalysis and numerical simulation,influence ofgravity field on thermodynamic properties of the system in strongmagnetic field is analyzed.It shows that,compared with the case of strong magnetic field only,gravity field makes the energy,chemical potential reduced.With rising temperature,influence of gravity field on chemical potential is gradually enlarged.There is amaximal influence of gravity field on heat capacity.Gravity fieldmakes oscillation of heat capacity almostunchangeablewhile oscillation center of chemical potential shift down.

gravity field；strongmagnetic field；Fermi gas；thermodynamic properties

1001-246X（2015）06-0751-06

O414.1；O414.2

A

2014－11－03；

2015－02－05

田青松（1988－）,男,硕士研究生,主要研究量子统计,E-mail：tqs728＠126.com